What is the distance from point D to point C?
A.1 unit
B.2 units
C.3 units
D.4 units

Answers
Answer:
the distance from point D to point C.
B.2 units
Answer:
B:-2
Step-by-step explanation:
just count the box and you will get your answer
Related Questions
Last year Anna read 20 books. 5 were non-fiction, 7 were graphic novels and 8 were mystery novels. What is the ratio of graphic novels to total books?
Answers
Answer:
7/20 or 7 out of 20 could be graphic novels
Step-by-step explanation:
Colon form: 7:20
-4x + 11y = 15
x = 2y
Answers
Answer:
x=10
y=5
Step-by-step explanation:
replace x in «-4x+11y=15» with 2y so it goes that way till you get y=5
Please answer 2,3, and 6
Possible answers:
SAS similarity theorem
Alternate interior
Corresponding
AA similarity Postulate
Substitution

Answers
Answer:
The given two column proof is completed as follows;
Statements \({}\) Reasons
1. \(\overline{BE}\) ║ \(\overline {CD}\) \({}\) 1. Given
2. ∠1 ≅ ∠2, ∠3 ≅ ∠4 \({}\) 2. Corresponding ∠s Post.
3. ΔABE ~ ΔACD \({}\) 3. AA similarity Postulate
4. \(\dfrac{AC}{AB} = \dfrac{AD}{AE}\) \({}\) 4. Def. of ~ Δs
5. AC = AB + BC; AD = AE + ED \({}\) 5. Segment Add. Post
6. \(\dfrac{AB + BC}{AB} = \dfrac{AE + ED}{AE}\) \({}\) 6. SAS Similarity Theorem
7. \(\dfrac{AB}{AB} + \dfrac{BC}{AB} = \dfrac{AE }{AE} + \dfrac{AE}{AE}\) \({}\) 7. Distributive property of equality
8. \(1 + \dfrac{BC}{AB} = 1 + \dfrac{AE}{AE}\) \({}\) \({}\) 8. \(Simplify \left(\dfrac{AB}{AB} =1; \dfrac{AE }{AE} =1\right)\)
9. \(\dfrac{BC}{AB} =\dfrac{AE}{AE}\) \({}\) \({}\) 9. Subtraction prop. of =
Step-by-step explanation:
The given two column proof is completed as follows;
Statements \({}\) Reasons
1. \(\overline{BE}\) ║ \(\overline {CD}\) \({}\) 1. Given
2. Corresponding angles are congruent (postulate)
3. Angle Angle, AA similarity Postulate
4. Def. of ~ Δs Definition of similar triangles
5. Segment Addition Postulate
6. Side-Angle-Side SAS Similarity Theorem
7. Distributive property of equality
8. \(1 + \dfrac{BC}{AB} = 1 + \dfrac{AE}{AE}\) \({}\) \({}\) 8. \(Simplify \left(\dfrac{AB}{AB} =1; \dfrac{AE }{AE} =1\right)\)
9. Subtraction property of equality, by subtracting 1 from both sides
Problems in Projection of Points: (Practice Questions) 1. Draw the projection of the following points. a) Point P, is 40 mm above HP and 55 mm in front of VP. (First Quadrant) b) Point Q, is 30 mm above HP and 45 mm behind VP. (Second Quadrant) c) Point R, is 35 mm below HP and 40 mm behind VP. (Third Quadrant) d) Point S, is 50 mm below HP and 30 mm in front of VP. (Fourth Quadrant) e) Point A, is 35 mm in front of VP. (lying on HP) f) Point B, is 30 mm behind VP. (Lying on HP) g) Point C, is 40 mm above HP. (Lying on VP) h) Point D, is 45 mm below HP. (Lying on VP) i) Point E, is on both HP and VP.(Lying on Reference Line XY)
Answers
The point where the horizontal and vertical lines intersect represents the projection of Point E.
To draw the projection of the given points, we need to use the principles of orthographic projection. Here's how the projections of each point would look like:
a) Point P: 40 mm above HP and 55 mm in front of VP (First Quadrant)
- Draw a horizontal line representing HP.
- From a point on HP, draw a vertical line upward representing the height above HP (40 mm).
- From the endpoint of the vertical line, draw a line parallel to XY representing the distance in front of VP (55 mm).
- The point of intersection of the parallel line with the vertical line represents the projection of Point P.
b) Point Q: 30 mm above HP and 45 mm behind VP (Second Quadrant)
- Draw a horizontal line representing HP.
- From a point on HP, draw a vertical line upward representing the height above HP (30 mm).
- From the endpoint of the vertical line, draw a line parallel to XY in the opposite direction representing the distance behind VP (45 mm).
- The point of intersection of the parallel line with the vertical line represents the projection of Point Q.
c) Point R: 35 mm below HP and 40 mm behind VP (Third Quadrant)
- Draw a horizontal line representing HP.
- From a point on HP, draw a vertical line downward representing the height below HP (35 mm).
- From the endpoint of the vertical line, draw a line parallel to XY in the opposite direction representing the distance behind VP (40 mm).
- The point of intersection of the parallel line with the vertical line represents the projection of Point R.
d) Point S: 50 mm below HP and 30 mm in front of VP (Fourth Quadrant)
- Draw a horizontal line representing HP.
- From a point on HP, draw a vertical line downward representing the height below HP (50 mm).
- From the endpoint of the vertical line, draw a line parallel to XY representing the distance in front of VP (30 mm).
- The point of intersection of the parallel line with the vertical line represents the projection of Point S.
e) Point A: 35 mm in front of VP (lying on HP)
- Draw a horizontal line representing HP.
- From a point on HP, draw a vertical line upward and downward representing the same height above and below HP (35 mm).
- The point where the vertical lines intersect HP represents the projection of Point A.
f) Point B: 30 mm behind VP (lying on HP)
- Draw a horizontal line representing HP.
- From a point on HP, draw a vertical line upward and downward representing the same height above and below HP.
- The point where the vertical lines intersect HP represents the projection of Point B.
- Since Point B is behind VP, the projection will not be visible.
g) Point C: 40 mm above HP (lying on VP)
- Draw a vertical line representing VP.
- From a point on VP, draw a horizontal line to the right representing the distance to the right of VP (40 mm).
- The point of intersection of the horizontal line with VP represents the projection of Point C.
h) Point D: 45 mm below HP (lying on VP)
- Draw a vertical line representing VP.
- From a point on VP, draw a horizontal line to the right representing the distance to the right of VP (45 mm).
- The point of intersection of the horizontal line with VP represents the projection of Point D.
i) Point E: On both HP and VP (lying on Reference Line XY)
- Draw a horizontal line representing HP.
- Draw a vertical line representing VP.
To know more about horizontal refer here:
https://brainly.com/question/29019854#
#SPJ11
what is the slope of (4,3) and (1,-1) the line is positive
Answers
The slope would be 1.33
The following statements are true generalizations. Imagine an exceptional case for each(that is, a situation in which the rule would not apply). 1. You should return what your borrow
Answers
1. The exceptional case where the rule "You should return what you borrow" would not apply is when the borrowed item is a consumable or disposable product.
In general, when you borrow something, it is expected that you will return it to the owner once you are done using it. This principle applies to various scenarios, such as borrowing books, tools, or household items. However, there are situations where returning what you borrow may not be applicable or practical.
For instance, consider borrowing a consumable item like a pack of disposable plates or a bottle of shampoo. These items are designed for one-time use and are meant to be consumed or disposed of. In such cases, returning what you borrow wouldn't make sense because the borrowed items are not intended for reuse. Instead, it is understood that the borrower will consume or utilize the entire item and will not be expected to return it.
Similarly, if you borrow something that is meant to be temporary or perishable, such as food items or fresh flowers, returning them would not be feasible or appropriate. These items have a limited lifespan and are not intended for long-term ownership or reuse.
It's important to note that the general rule of returning what you borrow primarily applies to items that are intended for multiple uses or have a longer lifespan. Exceptions arise when dealing with consumable or perishable goods, where the expectation of returning the borrowed item does not hold due to their nature of one-time use or limited lifespan.
Learn more about consumable here
https://brainly.com/question/20848500
#SPJ11
how to multiply matrices with different dimensions
Answers
The number of columns in the first matrix must equal the number of rows in the second matrix in order to multiply matrices with different dimensions.
First, jot down each matrix's dimensions. Let's imagine, for illustration, that we have a matrix A that is 2 by 3 and a matrix B that is 3 by 4. Create a new matrix C with the dimensions 2x4 in step 2. This is what the multiplication will ultimately produce.3. Determine the dot product of the corresponding row in matrix A and the corresponding column in matrix B for each element in matrix C.
4: The final response is matrix C, which is the union of the 2x3 matrix A and the 3x4 matrix B.
Therefore, the result is a 2x4 matrix, which is produced by taking the dot product of the rows and columns of matrix A and matrix B.
To know more about matrices at :
brainly.com/question/12088021
#SPJ4
which statement best explains why objects are pulled toward Earth's center?
Earth has a magnetic force that is strongest at its core.
Earth has a much greater mass than objects on its surface.
the way of the atmosphere pushes objects toward Earth surface.
the strength of the Sun's gravity pushes down on objects at Earth's surface.
I neeed the answerr nowwwwe.
Answers
answer
objects are pulled toward Earth's center? Earth has a magnetic force that is strongest at its core. Earth has a much greater mass than objects on its surface. The weight of the atmosphere pushes objects toward Earth's surface
Answer:
the answer is...... aStep-by-step explanation:
it right on edge 2020HELPP LOOK AT THE PHOTO

Answers
The scenario is represented by the simple equation \(10 + 2^7.\)
A pregnant rabbit will give birth to a litter of young rabbits during the first month. There will be 12 animals total at the end of the first month (\(10 + 2^1\)).
The final population can be represented by the equation \(10 + 2^7\) because the procedure lasts for 7 months.
\(10 + 2^7 = 10 + 128 = 138\)
What are equations?A mathematical definition of an equation is a claim that two expressions are equal when they are joined by the equals sign ("=").
Two expressions are combined in an equation using an equal symbol ("="). The "left-hand side" and "right-hand side" of the equation are the two expressions on either side of the equals sign. Typically, we consider an equation's right side to be zero. As we can balance this by deducting the right-side expression from both sides' expressions, this won't reduce the generality.
A condition on a variable is what an equation in algebra is. It can only be satisfied if the variable has a specific value. That means that only the value of x = 9 may satisfy the equation 2x - 5 = 13.
To know more about equations visit:
https://brainly.com/question/649785
#SPJ1
note: this is a multi-part question. once an answer is submitted, you will be unable to return to this part. 7 women and 7 men are on the faculty in the mathematics department at a school. how many ways are there to select a committee of five members of the department if at least one woman must be on the committee?
Answers
No. of ways of selecting the 5 member committee by combination= 1981
What are the number of ways of selecting the 5 member committee ?
No. of women faculty in the mathematics department = 7
No. of men faculty in the mathematics department = 7
Total number of faculty members = 14
Condition - at least one woman must be on the committee
No. of ways of selection = C (14, 5) - C (7, 5)
We know that combination C(n , r) = \(\frac{n!}{(n-r)!r!}\)
Consider the total combination C (14, 5),
\(C (14, 5)=\frac{14!}{9!5!} \\\\=\frac{14 *13* 12 *11 *10 *9!}{9!* 5!} \\\\=\frac{14 *13* 12 *11 *10}{120} \\\\= \frac{240240}{120} \\\\= 2002\)
Consider the combination of men C (7, 5) ,
\(C (7, 5)=\frac{7!}{2!5!} \\\\=\frac{7*6*5!}{2!* 5!} \\\\=\frac{7*6}{2} \\\\= 7*3\\\\=21\)
No. of ways of selection = C (14, 5) - C (7, 5)
= 2002 - 21
=1981
No. of ways of selecting the 5 member committee of the department with least one woman by combination= 1981
To learn more about combinations, refer:
https://brainly.com/question/4658834
#SPJ4
15-7 x 2 x 2 to the 3rd power
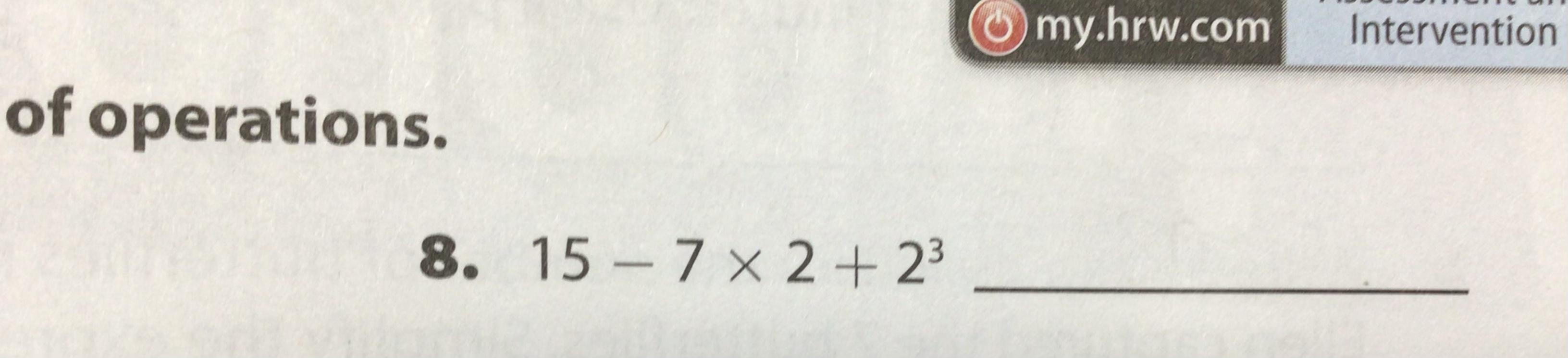
Answers
Answer:
5832
Step-by-step explanation:
15 - 7 = 8
8 × 2 = 16
16 + 2 = 18
18 × 18 × 18 = 5832
What is the median of the data set?
I will give Brainliest to the best answer only if it is Brainly Expert
A. 10
B. 8.5
C. 8
D. 9

Answers
Answer:
The answer to your problem is, A. 10
Step-by-step explanation:
So first add up all the total number of ‘ X ‘
Which is:
4 + 3 + 2 + 1 = 10
Technically 10 is our answer.
Thus the answer to your problem is, A. 10
Not a 100% sure
Answer:
5, 8, 8, 8, 8, 9, 9, 9, 10, 10
The median of this data set is 8.5, so the correct answer is B.
Step-by-step explanation:
Since there are 10 observations, we are looking for the number halfway between the two middle observations (observations #5 and #6) when the data are arranged in order. Here, observation #5 is 8, and observation #6 is 9, so the median of this data set is (8 + 9)/2 = 8.5. B is the correct answer.
£14,000 was deposited in a savings account that pays simple interest. After 11 years, the account contains £17,850. Work out the annual interest rate of the account. Give your answer as a percentage (%) to 1 d.p.
Answers
The annual interest rate of the account after 11 years is 2.5%
What is the annual interest rate of the account?Principal, P = £14,000
Time, T = 11 years
Rate = ?
Simple interest = £17,850 - £14,000 = £3,850
Simple interest = (Principal × Rate × Time) / 100
3,850 = (14,000 × Rate × 11) / 100
3850 = 154,000R / 100
3850 = 1,540R
Divide both sides by 1,540
R = 3,850 / 1540
R = 2.5%
Therefore, 2.5% is the annual interest rate?
Read more on simple interest:
https://brainly.com/question/20690803
#SPJ1
what is nine and forty-two hundredths
Answers
Answer:
9.42
Step-by-step explanation:
Breaking the phrase down:
'Nine' would be the number 9 in the ones place.
'And' represents the decimal in a number. ('.')
'Forty-Two Hundredths" is 0.42.
So, "nine and forty-two hundredths" would be 9.42.
Hope this helps.
For f(x) = -x + 8, which statement is true?
Answers
The volume of a cylinder is 448 pi cm³ and the height is 7 cm.Find its radius.
Answers
The formula for the volume of a cylinder is given by:
\(V=\pi r^2h\)Where r is the base radius and h is the height.
If the volume is 448*pi cm³ and the height is 7 cm, we have:
\(\begin{gathered} 448\pi=\pi r^2\cdot7\\ \\ 448=7r^2\\ \\ r^2=\frac{448}{7}\\ \\ r^2=64\\ \\ r=8\text{ cm} \end{gathered}\)Therefore the radius is equal to 8 cm.
Drawing this cylinder, we have:
James and Amy each improved their yards by planting sod and geraniums. They bought their supplies from the same store. James spent $66 on 2 ft of sod and 4 geraniums. Amy spent $55 on 1 ft of sod and 4 geraniums. Find the cost of one ft of sod and the cost of one geranium.
Answers
ANSWER
• One foot of sod: $11
,• One geranium: $11
EXPLANATION
First, name the variables:
• x: cost of 1 foot of sod
,• y: cost of 1 geranium
We know that James spent $66 buying 2 feet of sod - which cost 2x, and 4 geraniums - which cost 4y.
Also, Amy spent $55 on 1 ft of sod - with a cost of x, and 4 geraniums - with a cost of 4x.
We have the system of equations,
\(\begin{cases}2x+4y=66 \\ x+4y=55\end{cases}\)Solve using elimination - i.e. subtract the second equation from the first,
Hence, one foot of sod costs $11.
To find the cost of one geranium we have to replace x = 11 in one of the equations. Replacing in the second equation,
\(11+4y=55\)And solve for y. Subtract 11 from both sides,
\(\begin{gathered} 11-11+4y=55-11 \\ 4y=44 \end{gathered}\)And divide both sides by 4,
\(\begin{gathered} \frac{4y}{4}=\frac{44}{4} \\ \\ y=11 \end{gathered}\)Hence, one geranium costs $11
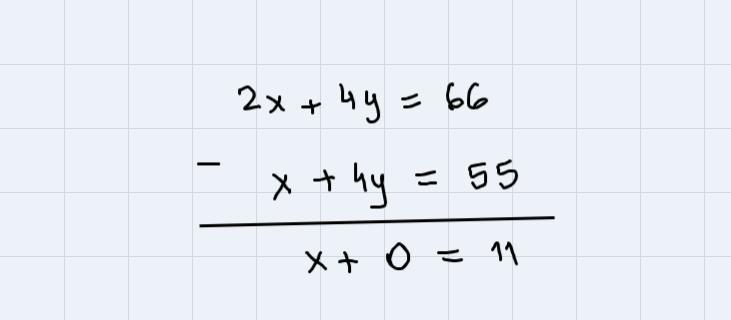
Find the 5th term of the
sequence: -8,-1, 6, 13...
Answers
Answer:
20
Step-by-step explanation:
you add 7 each time
Answer:
20
Step-by-step explanation:
Find the pattern: +7. so the next one is 13+7 which is 20.
Hope this helps plz mark brainliest :D
Computer equipment was acquired at the beginning of the vear at a cout of $73,700 that has an estimatod resduat value of 34,600 and an eatimated ustul life of 5years. a. Determine the depreciable cost. b. Determine the straight-tine rate. \% c. Determine the annual straight-hine depreciation.
Answers
The computer equipment was acquired at a cost of $73,700 with an estimated residual value of $34,600 and a useful life of 5 years. The depreciable cost of the equipment is $39,100. The straight-line rate is 20%, and therefore, the annual straight-line depreciation for the computer equipment is $7,820.
a. To determine the depreciable cost, we subtract the estimated residual value from the initial cost: $73,700 - $34,600 = $39,100.
b. The straight-line rate is calculated by dividing 100% by the estimated useful life of the equipment. In this case, the straight-line rate is 100% / 5 = 20% per year.
c. The annual straight-line depreciation is found by multiplying the depreciable cost by the straight-line rate. Thus, the annual depreciation is $39,100 * 20% = $7,820 per year.
By following these calculations, we can determine that the depreciable cost of the computer equipment is $39,100, the straight-line rate is 20%, and the annual straight-line depreciation amounts to $7,820.
Learn more about depreciation here:
https://brainly.com/question/17827672
#SPJ11
Events D and E are independent, with P(D)- 0.6 and P(D and E) - 0.18. Which of the following is true? A. P(E)- 0.12 B. P(E) = 0.4 C. P(D or E)-0.28 D. P(D or E) 0.72 E. P(D or E)-0.9
Answers
The correct statement is: A. P(E) = 0.3. The probability of event E, denoted as P(E), is equal to 0.3.
To determine the correct answer, let's analyze the given information.
We know that events D and E are independent, which means that the occurrence of one event does not affect the probability of the other event happening.
Given:
P(D) = 0.6
P(D and E) = 0.18
Since events D and E are independent, the probability of both events occurring (P(D and E)) can be calculated as the product of their individual probabilities:
P(D and E) = P(D) * P(E)
Substituting the given values:
0.18 = 0.6 * P(E)
To find the value of P(E), we can rearrange the equation:
P(E) = 0.18 / 0.6
P(E) = 0.3
Therefore, the correct answer is A. P(E) = 0.3.
Learn more about probability here: https://brainly.com/question/32117953
#SPJ11
-2.2 = x - 4.2
solve for x
Answers
Answer:
2
Step-by-step explanation:
Add 4.2 to both sides
x = 2
hree hundred books sell for 40 dollars each, resulting in a revenue of 12,000 dollars. For each $5 increase in the price, 25 fewer books are sold. Write the revenue R as a function of the number x of $ 5 increases.
Answers
A total of 12,000 dollars is made from the sale of 300 books at a price of $40 each. 25 fewer books are sold for every $5 increase in price. R(x)=(40+5x)(300−25x) R ( x ) = ( 40 + 5 x ) ( 300 − 25 x )
What is the revenue R as a function of number x ?Assumed in this instance is , At a price of 40 dollars apiece, \($(300)(40 \$)=12,000 \$$\) books generate $300 in revenue. The result is that 25 fewer books are sold if we raise the price of each book by $5. That's \($(300-25 x)$\). Due to the fact that the price always rises by five times more than the number of books, the cost is \($(40+5 x)$\).
\($R=(300-25 x) \cdot(40+5 x)$\)
\($R=12000+6000 x-1000 x-125 x^2$\\$R=-125 x^2+5000 x+12000$\\$R=125 x^2-5000 x-12000$\)
The revenue R is expressed as a function of the number x as it approaches 5. R(x)=(40+5x)(30025x) is the necessary revenue function. R(x) = (40 + 5 x)(300 25 x) is the necessary revenue function.
To learn more about revenue refer to :
https://brainly.com/question/2263738
#SPJ4
cube root of 8 x 10 to the power of 6
\( \sqrt[3]{8 \times {10}^{6} } \)
Answers
Answer:
The answer is 200.
Step-by-step explanation:
The steps are :
\( \sqrt[3]{8 \times {10}^{6} } \)
\( = \sqrt[3]{8} \times \sqrt[3]{ {10}^{6} } \)
\( = {8}^{ \frac{1}{3} } \times {10}^{(6 \times \frac{1}{3} )} \)
\( = 2 \times {10}^{2} \)
\( = 200\)
help me pleasee i need help this is my final btw

Answers
Answer:
12 sq units
Step-by-step explanation:
height = 3
length = 4
A = l · w
A = 12
I need help ASAP!!!!!!

Answers
Answer:
Not a function
Step-by-step explanation:
create the left-ist heap using these values: 74 77 12 83 54 15 24 29 86 80
Answers
A left-ist heap is a type of binary tree where the value of each node is greater than or equal to the values of its children. To create a left-ist heap, we can follow these steps:
Start with the first value as the root of the heap.
Insert the remaining values one by one into the heap by merging them with the existing heap.
Here is the left-ist heap created using the given values: 74, 77, 12, 83, 54, 15, 24, 29, 86, 80
Step 1: Create the initial heap with the first value:
74
Step 2: Insert the remaining values one by one:
Insert 77: Merge with the existing heap:
74
/
77
Insert 12: Merge with the existing heap:
12
/
74 77
Insert 83: Merge with the existing heap:
12
/
74 77
/
83
Insert 54: Merge with the existing heap:
12
/
54 77
/ /
74 83
Insert 15: Merge with the existing heap:
12
/
15 77
/ \ /
54 74 83
Insert 24: Merge with the existing heap:
12
/
15 77
/ \ /
24 54 74 83
Insert 29: Merge with the existing heap:
12
/
15 77
/ \ /
24 29 74 83
Insert 86: Merge with the existing heap:
12
/
15 77
/ \ /
24 29 74 83
86
Insert 80: Merge with the existing heap:
12
/
15 77
/ \ /
24 29 74 83
/
80 86
The resulting left-ist heap using the given values is:
12
/ \
15 77
/ \ / \
24 29 74 83
/ \
80 86
To learn more about binary : brainly.com/question/33333942
#SPJ11
please help!! ill give brainliest + points!!

Answers
Answer:
A
Step-by-step explanation:
There are 135 people in a sport centre. 73 people use the gym. 73 people use the swimming pool. 67 people use the track. 36 people use the gym and the pool. 35 people use the pool and the track. 32 people use the gym and the track. 14 people use all three facilities. A person is selected at random. What is the probability that this person doesn't use any facility?
Answers
Answer:
P = 11/135 = 0.0815
Step-by-step explanation:
we can said that:
14 people use all three facilities18 people use just gym and track (32 people use the gym and the track less the 14 people that use all three facilities)21 people use just pool and track (35 people use the pool and the track less the 14 people that use all three facilities)22 people use just gym and pool (36 people use the gym and the pool less the 14 people that use all three facilities)14 people use just the track (67 people use the track less the 18 people that use just the gym and the track, the 21 people that use just the pool and the track and 14 people that use all three facilities)16 people use just the pool (73 people use the swimming pool less the the 21 people that use just the pool and the track, the 22 people that use just the gym and the pool and 14 people that use all three facilities)19 people use just the gym (73 people use the gym less the 18 people that use just the gym and the track, the 22 people that use just the gym and the pool and 14 people that use all three facilities)So, there are 124 people that use the gym, the pool or the track. This is calculated using the information above as:
14 + 18 + 21 + 22 + 14 + 16 + 19 = 124
Finally, there are 11 ( 135 - 124 = 11 ) people that don't use any facility, so the probability that a person doesn't use any facility is:
P = 11/135 = 0.0815
Answer:
0.0815
Step-by-step explanation:
A social media website had 700,000 followers in 2014. The number y of followers increases by 6% each year.
a. Write an exponential growth function that represents the number of followers t years after 2014.
b. How many people will be following the website in 2019. Round your answer to the nearest thousand.
Answers
b. 2 years later which means t=2, hence, y=700,000*(1+6%)^2=786520
round to the nearest thousand: y=78700
whats -6a+3=-3(2a-3) solution
Answers
infinite solutions cuz 0=6
☽------------❀-------------☾
Hi there!
~
\(-6a+3=-3(2a-3)\)
\(0 = 6\)
There are no solutions.
❀Hope this helped you!❀
☽------------❀-------------☾