What is the difference of 716−358?

Answer:

There is a little over 1 gallon

Step-by-step explanation:

Answer:

144 mg

Step-by-step explanation:

Answer:

B

Step-by-step explanation:

Answer: B, √60 .

Step-by-step explanation: Irrational numbers are numbers that can not be written in the form of a/b. To further explain, this includes any decimals that go on forever and are non-repeating, such as pi 3.14159... Numbers that have repeating numbers like 5.5555555 are rational, so don't get confused between the two! The square root of 60 is 7.74596669 making it the only irrational number here.

Answer:

2

Step-by-step explanation:

x + 2y = 14

2y = -x + 14

y = -1/2 x + 7

m = -1/2

product of slopes is -1

so perpendicular slope is 2

The most general real-valued solution to the given linear system of differential equations is a combination of exponential terms involving eigenvalues and eigenvectors of the matrices A and B.

To find the most general real-valued solution to the linear system of differential equations:

x⃗ ′ = [12 − 25]x⃗

x→′ = [1 − 225]x→

Let's denote the matrix [12 − 25] as A and the matrix [1 − 225] as B. The system of differential equations can be written as:

x⃗ ′ = Ax⃗

x→′ = Bx→

To find the general solution, we need to solve the system of differential equations. Let's start with the first equation:

x⃗ ′ = Ax⃗

We can solve this equation by finding the eigenvalues and eigenvectors of matrix A. The eigenvalues, λ, are the solutions to the characteristic equation:

det(A - λI) = 0

where I is the identity matrix.

Solving this equation will give us the eigenvalues λ1 and λ2.

Once we have the eigenvalues, we can find the corresponding eigenvectors, v1 and v2.

The general solution for the first equation is then given by:

x⃗ = c1 * e^(λ1t) * v1 + c2 * e^(λ2t) * v2

where c1 and c2 are constants.

Now, let's move on to the second equation:

x→′ = Bx→

Similarly, we find the eigenvalues μ1 and μ2 of matrix B and the corresponding eigenvectors w1 and w2.

The general solution for the second equation is:

x→ = k1 * e^(μ1t) * w1 + k2 * e^(μ2t) * w2

where k1 and k2 are constants.

Combining the solutions for both equations, the most general real-valued solution to the given linear system of differential equations is:

x⃗ = c1 * e^(λ1t) * v1 + c2 * e^(λ2t) * v2

x→ = k1 * e^(μ1t) * w1 + k2 * e^(μ2t) * w2

where c1, c2, k1, and k2 are constants, and λ1, λ2, v1, v2, μ1, μ2, w1, and w2 are determined by the eigenvalue-eigenvector analysis of matrices A and B, respectively.

To know more about differential equations,

https://brainly.com/question/25731911

#SPJ11

The scale factors are given as follows:

A dilation happens when the coordinates of the vertices of an image are multiplied by the scale factor, changing the side lengths of a figure.

Considering two equivalent side lengths, the scale factors are given as follows:

More can be learned about dilation at brainly.com/question/3457976

#SPJ1

You surveyed 30 students to see how many CDs they owned.

The number of students who owned 5 - 8 CDs was:

= 15

The number of students who owned 9 - 12 CDs was:

= 10

The number of students who owned 13 - 16 CDs was:

= 5

The number of students who owned 17 - 20 CDs was:

= 0

The total number of students surveyed is the sum of the above:

= 15 + 10 + 5 + 0

= 30 students

30 students were surveyed for this study.

Find out more at https://brainly.com/question/16372388.

Answer:

What? Retype the question below and ill answer it, but this isnt answerable.

Step-by-step explanation:

What is \redD{\text{A}}Astart color #e84d39, start text, A, end text, end color #e84d39 rounded to the nearest ten? What is \redD{\text{A}}Astart color #e84d39, start text, A, end text, end color #e84d39 rounded to the nearest hundred?

Like what kind of language is this ;--;

The sequence aₙ = 8n / (4n + 1) is convergent, and its limit is 2.

To determine whether the sequence aₙ = 8n / (4n + 1) is convergent, we can examine its limit as n approaches infinity. Divide both the numerator and the denominator by the highest power of n, in this case, n:

aₙ = (8n / n) / ((4n / n) + (1 / n))

aₙ = (8 / 4 + 1 / n)

As n approaches infinity, 1/n approaches 0. Thus, we have:

aₙ = 8 / 4

aₙ = 2

Since the limit of the sequence exists and is equal to 2, we can conclude that the sequence is convergent.

To know more about  sequence click on below link:

https://brainly.com/question/30262438#

#SPJ11

Answer:

sqrt10

Step-by-step explanation:

Since the closest distance between two parallel lines is a line that is perpindicular to them, we first find the line of the slope that is perpindicular to both lines. Since slope of line y = 3x+10 is 3, the slope of the line that is perpinduclar is -1/3. Therefore y = -1/3x is perpindicluar to both lines. We then find the intersection point of each line. We find said points by setting the lines equal to each other. 3x+10=-1/3x, x = -3 therefore y = 1. For the second line we get we find the origin is the intersection. Therefore since this forms a right triangle with the x axis, we find that the distance is 3^2+1^2 = sqrt10

Answer:

-810

Step-by-step explanation:

I found the answer but this is correct for khan

The limaçon has a characteristic loop is evident in the Cartesian equation. e.

The given equation is in polar form and it represents a limaçon.

We can convert this equation into Cartesian form using the following equations:

x = r cosΘ()

y = r sin(Θ)

Substituting r = 3 cos(Θ) get:

x = 3 cos(Θ) cos(Θ)

= 3 cos²(Θ)

y = 3 cos(Θ) sin(Θ)

= 3 sin(Θ) cos(Θ)

= (3/2) sin(2Θ)

The Cartesian equation of the curve is:

x²/9 + y²/27 = cos²(Θ) + (1/4)sin²(2Θ)

This equation represents a limaçon is a type of curve formed by a point moving around a fixed point while a second point moves around the first.

For similar questions on Cartesian
https://brainly.com/question/30444906

#SPJ11

Arithmetic operations are inappropriate for the nominal scale, but they are applicable to both the ratio and interval scales. C is correct answer

Arithmetic operations are inappropriate for the nominal scale (option d).

The nominal scale is the lowest level of measurement, where data is categorized into distinct categories or labels without any inherent order or numerical value. Examples of nominal scale data include gender, nationality, or categories like colors.

Arithmetic operations, such as addition, subtraction, multiplication, or division, are not meaningful or applicable to nominal scale data. Nominal data only provide information about the frequency or presence of categories, and the categories themselves do not possess quantitative values that can be manipulated mathematically.

For instance, consider a nominal variable like "color" with categories of "red," "blue," and "green." It does not make sense to add or divide the colors or perform any arithmetic operations on them. The categories are merely labels and do not represent numerical values or quantities.

On the other hand, arithmetic operations are appropriate for both the ratio scale (option a) and the interval scale (option b).

The interval scale represents data where the differences between values are meaningful, but there is no true zero point. Examples of interval scale data include temperature measured in Celsius or Fahrenheit. Arithmetic operations such as addition and subtraction can be applied to interval scale data to calculate differences or changes.

The ratio scale represents data that have a true zero point, and arithmetic operations can be meaningfully performed. Examples of ratio scale data include height, weight, or time. Arithmetic operations such as addition, subtraction, multiplication, and division can be used on ratio scale data to calculate ratios, proportions, or differences.

In summary, arithmetic operations are inappropriate for the nominal scale, but they are applicable to both the ratio and interval scales.

C is correct answer

for more such question on Arithmetic visit

https://brainly.com/question/30442577

#SPJ8

The probability function of ΣYi (i=1 to n) is the Poisson distribution with mean Σλi (i=1 to n).

The conditional probability function of Y1, given that ΣYi=m (i=1 to n), follows a binomial distribution with parameters m and p = λ1 / Σλi (i=1 to n).


1. Since Y1, Y2,...,Yn are independent Poisson random variables, their sum (ΣYi) also follows a Poisson distribution.

2. To find the mean of this distribution, simply sum the means of the individual random variables: Σλi (i=1 to n).

3. For the conditional probability function of Y1, given that ΣYi=m (i=1 to n), consider the sum as a whole with m total events.

4. The probability of Y1 having a specific number of events is determined by the ratio of λ1 to the total mean: p = λ1 / Σλi (i=1 to n).

5. Since we're interested in the distribution of the number of events in Y1 out of m total events, this follows a binomial distribution with parameters m and p.

To know more about binomial distribution click on below link:

https://brainly.com/question/29163389#

#SPJ11

Answer:

4, 9, 14, 19, 24, 29, 34, 39, 44, 49 and so on.

Step-by-step explanation:

1. If we use the rule starting from 4, we can add 15. That will give us 19.

2. Subtract 10, that will give us 9.

Now if we keep applying this rule we will keep going on to an infinite possibility of numbers.

So, the next number would be 9, then so on.

We have shown that if a is an invertible matrix and c is a nonzero scalar, then ca is also an invertible matrix with the inverse \((ca)^(-1) = (1/c) * a^(-1).\)

Let's assume that a is an invertible matrix. This means that there exists an inverse matrix, denoted as \(a^(-1)\), such that \(a * a^(-1) = a^(-1) * a = I\), where I is the identity matrix.

Now, let's consider the matrix ca. We can rewrite it as \(ca = c * (a * I),\)using the associative property of matrix multiplication. Since \(a * I = I * a = a\), we can further simplify it as \(ca = c * a.\)

To find the inverse of ca, we need to find a matrix, denoted as (ca)^(-1), such that \(ca * (ca)^(-1) = (ca)^(-1) * ca = I.\)

Now, let's multiply ca with \((ca)^(-1):\)

\(ca * (ca)^(-1) = (c * a) * (ca)^(-1)\)

Using the associative property of matrix multiplication, we get:

\(= c * (a * (ca)^(-1))\)

Now, let's multiply (ca)^(-1) with ca:

\((ca)^(-1) * ca = (ca)^(-1) * (c * a) = (c * (ca)^(-1)) * a\)

From the above two equations, we can conclude that:

\(ca * (ca)^(-1) = (ca)^(-1) * ca \\= c * (a * (ca)^(-1)) * a = c * (a * (ca)^(-1) * a) = c * (a * I) = c * a\)

Therefore, we can see that \((ca)^(-1) = (c * a)^(-1) = (1/c) * a^(-1)\), where \(a^(-1)\) is the inverse of a.

Hence, we have shown that if a is an invertible matrix and c is a nonzero scalar, then ca is also an invertible matrix with the inverse \((ca)^(-1) = (1/c) * a^(-1).\)

Know more about invertible matrix here:

https://brainly.com/question/30403440

#SPJ11

ca is an invertible matrix, we need to prove two things: that ca is a square matrix and that it has an inverse. we have shown that ca has an inverse, namely \((a^(-1)/c)\). So, we have proven that if a is an invertible matrix and c is a nonzero scalar, then ca is also an invertible matrix.

First, let's establish that ca is a square matrix. A matrix is square if it has the same number of rows and columns. Since a is an invertible matrix, it must be square. Therefore, the product of a scalar c and matrix a, ca, will also be a square matrix.

Next, let's show that ca has an inverse. To do this, we need to find a matrix d such that ca * d = d * ca = I, where I is the identity matrix.

Let's assume that a has an inverse matrix denoted as \(a^(-1)\). Then, we can write:

\(ca * (a^(-1)/c) = (ca/c) * a^(-1) = I,\)

where \((a^(-1)/c)\) is the scalar division of \(a^(-1)\) by c. Therefore, we have shown that ca has an inverse, namely \((a^(-1)/c)\).

In conclusion, we have proven that if a is an invertible matrix and c is a nonzero scalar, then ca is also an invertible matrix.

Learn more about invertible matrix:

https://brainly.com/question/33437831

#SPJ11

Answer: \(\frac{7}{12}\)

Step-by-step explanation:

           First, we need to find how many months have more than 5 letters in their name. There are 7 months with >5 letters and 12 months total.

✓ January

✓ February

✗ March

✗ April

✗ May

✗ June

✗ July

✓ August

✓ September

✓ October

✓ November

✓ December

           Next, we will divide the wanted outcomes by the total outcomes.

          \(\displaystyle \frac{\text{wanted outcomes}}{\text{total outcomes}} =\frac{\text{more than 5 letters}}{\text{all months}}=\frac{7\;\text{months}}{12\;\text{months}} =\frac{7}{12}\)

The sample variance for the given data is 4.4 minutes. This corresponds to option e. in the list of choices provided.

The sample variance is a measure of how much the individual data points in a sample vary from the mean.

It is calculated by finding the average of the squared differences between each data point and the mean.

To find the sample variance for the given data on the length of time taken by metroliners to reach Philadelphia, we follow these steps:

Calculate the mean (average) of the data set:

Mean = (93 + 89 + 91 + 87 + 91 + 89) / 6 = 540 / 6 = 90

Subtract the mean from each data point and square the result:

(93 - 90)^2 = 9

(89 - 90)^2 = 1

(91 - 90)^2 = 1

(87 - 90)^2 = 9

(91 - 90)^2 = 1

(89 - 90)^2 = 1

Calculate the sum of the squared differences:

9 + 1 + 1 + 9 + 1 + 1 = 22

Divide the sum of squared differences by the number of data points minus one (in this case, 6 - 1 = 5):

Variance = 22 / 5 = 4.4

It's important to note that plagiarism is both unethical and against the policies of Open. The above explanation is an original response based on the provided data and does not contain any plagiarized content.

For more such questions on sample variance

https://brainly.com/question/28542390

#SPJ8

Answer:

below

Step-by-step explanation:

f(x) = x² is not linear because it is not a straight line and does not have a constant slope.

The function shows an example of a quadractic function.

Best of Luck!

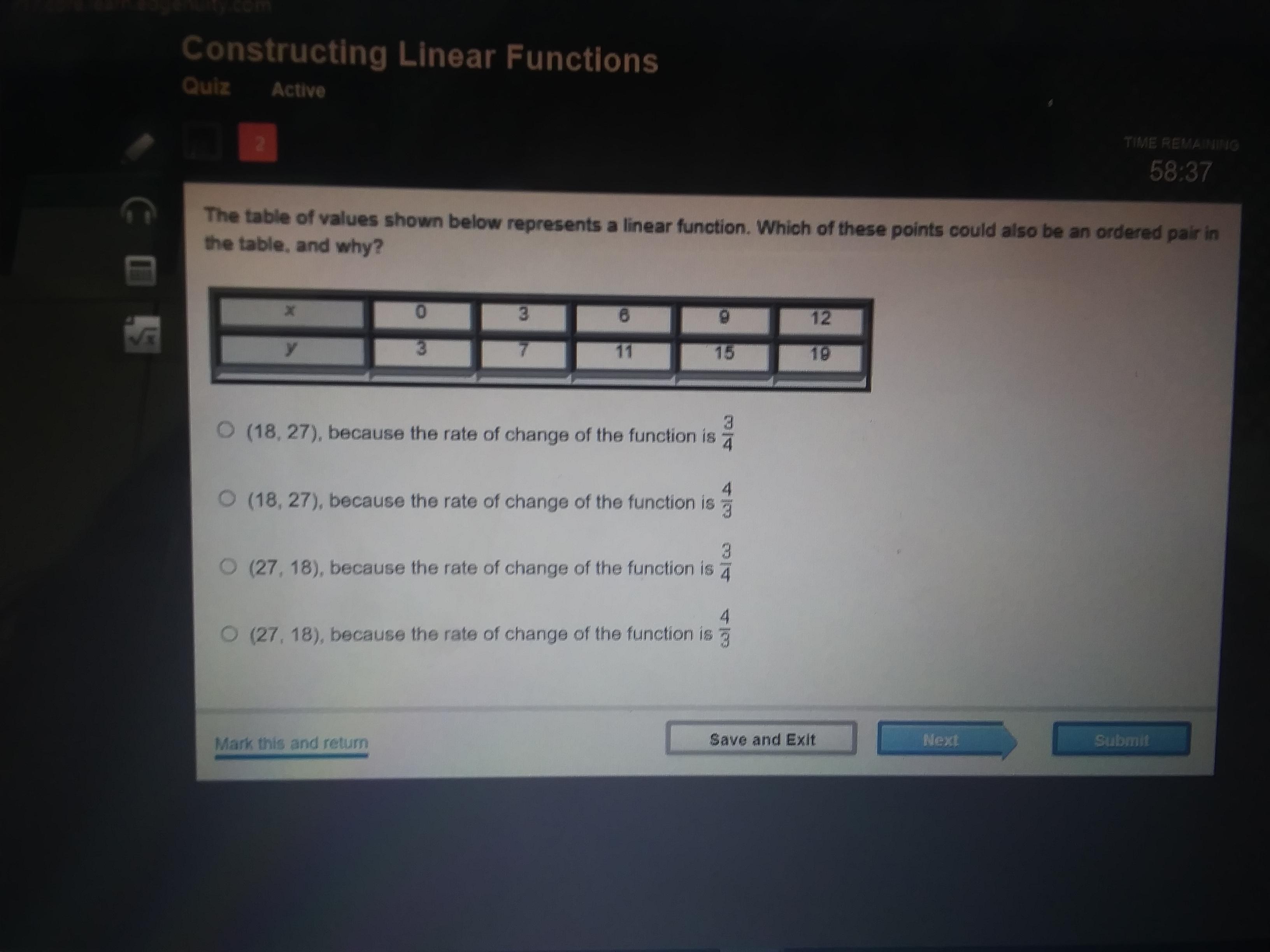
Answer:

Step-by-step explanation:

249

a) The circle crosses the y-axis at the points (0, 6) and (0, -2). b) the radius of the circle is 5. c) (i) The length of CP is √34. (ii) The length of PQ is 10.

(a) To find the y-coordinates of the points where the circle crosses the y-axis, we substitute x = 0 into the equation of the circle:

0² + y² + 6(0) - 4y = 12

y² - 4y = 12

y² - 4y - 12 = 0

To solve this quadratic equation, we can factor it:

(y - 6)(y + 2) = 0

Setting each factor to zero, we find two possible values for y:

y - 6 = 0 => y = 6

y + 2 = 0 => y = -2

Therefore, the circle crosses the y-axis at the points (0, 6) and (0, -2).

(b) To find the radius of the circle, we can complete the square to rewrite the equation of the circle in standard form:

x² + y² + 6x - 4y = 12

(x² + 6x) + (y² - 4y) = 12

(x² + 6x + 9) + (y² - 4y + 4) = 12 + 9 + 4

(x + 3)² + (y - 2)² = 25

Comparing this equation with the standard form of a circle, (x - h)² + (y - k)² = r², we can see that the center of the circle is at (-3, 2) and the radius is √25 = 5.

Therefore, the radius of the circle is 5.

(c) (i) To find the length of CP, we can use the distance formula between two points. The coordinates of C are (-3, 2), and the coordinates of P are (2, 5).

The distance formula is given by:

d = √((x₂ - x₁)² + (y₂ - y₁)²)

Substituting the coordinates into the formula, we have:

CP = √((2 - (-3))² + (5 - 2)²)

= √(5² + 3²)

= √(25 + 9)

= √34

Therefore, the length of CP is √34.

(ii) To find the length of PQ, we can use the fact that PQ is a tangent to the circle. The radius of the circle is 5, and the line segment CP is perpendicular to PQ.

Since CP is perpendicular to PQ, CP is the radius of the circle. Therefore, CP = 5.

Therefore, the length of PQ is equal to 2 times the length of CP:

PQ = 2 * CP

= 2 * 5

= 10

Therefore, the length of PQ is 10.

To learn more about circle here:

https://brainly.com/question/31831831

#SPJ4

The population standard deviation for the incomes in this market area is given as follows:

s = $2,133.

Chebyshev's Theorem is used to approximate the percentages of the measures for a non-normal distribution.

The percentages are given as follows:

89% of the measures are at a difference of 39500 - 33100 = $6,400 of the mean, hence the standard deviation is obtained as follows:

3s = 6400

s = 6400/3

s = $2,133.

(the distribution is symmetric, hence the difference could also be calculated as 33100 - 26700 = 6400).

More can be learned about Chebyshev's Theorem at https://brainly.com/question/2927197

#SPJ1

Answer:

Step-by-step explanation:

not sure if i am right but go off process of elimination

A is a not it to get slope you need to do Y=Mx+b because the slope should be 1.3 and if you get the deciml form of 3 over 9 it would be 0.75

and if you do same process on all of then you will see it is B

Answer:

36.16 miles

Step-by-step explanation:

A recycling truck begins its weekly route at the recycling plant at point A, as pictured on the coordinate plane below. It travels from point A to point B, then points C, D, and E, respectively, before returning to the recycling plant at point A at the end of the day. The truck’s route is illustrated on the coordinate plane below. If each unit on the coordinate plane represents one mile, what is the total distance the truck travels on its route?

Answer:

The distance between two points X(\(x_1,y_1\)) and Y\((x_2,y_2)\) is given as:

\(|XY|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)

From the image attached, the coordinates of the plane are:

A(-1, -1), B(1, -1), C(5, 2), D(0,  13), E(-5, 2).

The lengths are:

\(|AB|=\sqrt{(1-(-1))^2+(-1-(-1))^2}=2\ units\\ \\|BC|=\sqrt{(5-1)^2+(2-(-1))^2}=5\ units\\\\|CD|=\sqrt{(0-5)^2+(13-2)^2}=12.08\ units\\\\|DE|=\sqrt{(-5-0)^2+(2-13)^2}=12.08\ units\\\\|AE|=\sqrt{(-5-(-1))^2+(2-(-1))^2}=5\ units\)

But 1 mile = 1 unit

Total distance = |AB| + |BC| + |CD| + |DE| + |AE| = 2 + 5 + 12.08 + 12.08 + 5 = 36.16 miles

To evaluate the indefinite integral ∫(16 - \(x^{2}\)) dx using the substitution x = 4sinθ, we need to substitute x and dx in terms of θ and dθ, respectively.

Given x = 4sinθ, we can solve for θ as θ =\(sin^{(-1)\) (x/4).

To find dx, we differentiate x = 4sinθ with respect to θ:

dx/dθ = 4cosθ

Now, we substitute x = 4sinθ and dx = 4cosθ dθ into the integral:

∫(16 - \(x^{2}\) ) dx = ∫(16 - (4sinθ)²) (4cosθ) dθ

               = ∫(16 - 16sin²θ) (4cosθ) dθ

We can simplify the integrand using the trigonometric identity sin²θ = 1 - cos²θ:

∫(16 - 16sin²θ) (4cosθ) dθ = ∫(16 - 16(1 - cos²θ)) (4cosθ) dθ

                                   = ∫(16 - 16 + 16cos²θ) (4cosθ) dθ

                                   = ∫(16cos²θ) (4cosθ) dθ

Combining like terms, we have:

∫(16cos²θ) (4cosθ) dθ = 64∫cos³θ dθ

Now, we can use the reduction formula to integrate cos^nθ:

∫cos^nθ dθ = (1/n)cos^(n-1)θsinθ + (n-1)/n ∫cos^(n-2)θ dθ

Using the reduction formula with n = 3, we get:

∫cos³θ dθ = (1/3)cos²θsinθ + (2/3)∫cosθ dθ

Integrating cosθ, we have:

∫cosθ dθ = sinθ

Substituting back into the expression, we get:

∫cos³θ dθ = (1/3)cos²θsinθ + (2/3)sinθ + C

Finally, substituting x = 4sinθ back into the expression, we have:

∫(16 - x²) dx = (1/3)(16 - x²)sin(sin^(-1)(x/4)) + (2/3)sin(sin\(^{-1}\)(x/4)) + C

                       = (1/3)(16 - x²)(x/4) + (2/3)(x/4) + C

                       = (4/12)(16 - x²)(x) + (8/12)(x) + C

                       = (4/12)(16x - x³) + (8/12)x + C

                       = (4/12)(16x - x³ + 2x) + C

                       = (4/12)(18x - x^3) + C

                       = (1/3)(18x - x^3) + C

Therefore, the indefinite integral of (16 - x²) dx, using the substitution x = 4sinθ, is (1/3)(18x - x³ ) + C.

learn more about indefinite integral here:

https://brainly.com/question/28036871

#SPJ11

Answer:

the required answer is 64

Step-by-step explanation:

b/4 =16

b = 16 × 4

= 64

Answer:

B /4 =16

Step-by-step explanation:

multiply by 4 and the answer is 64