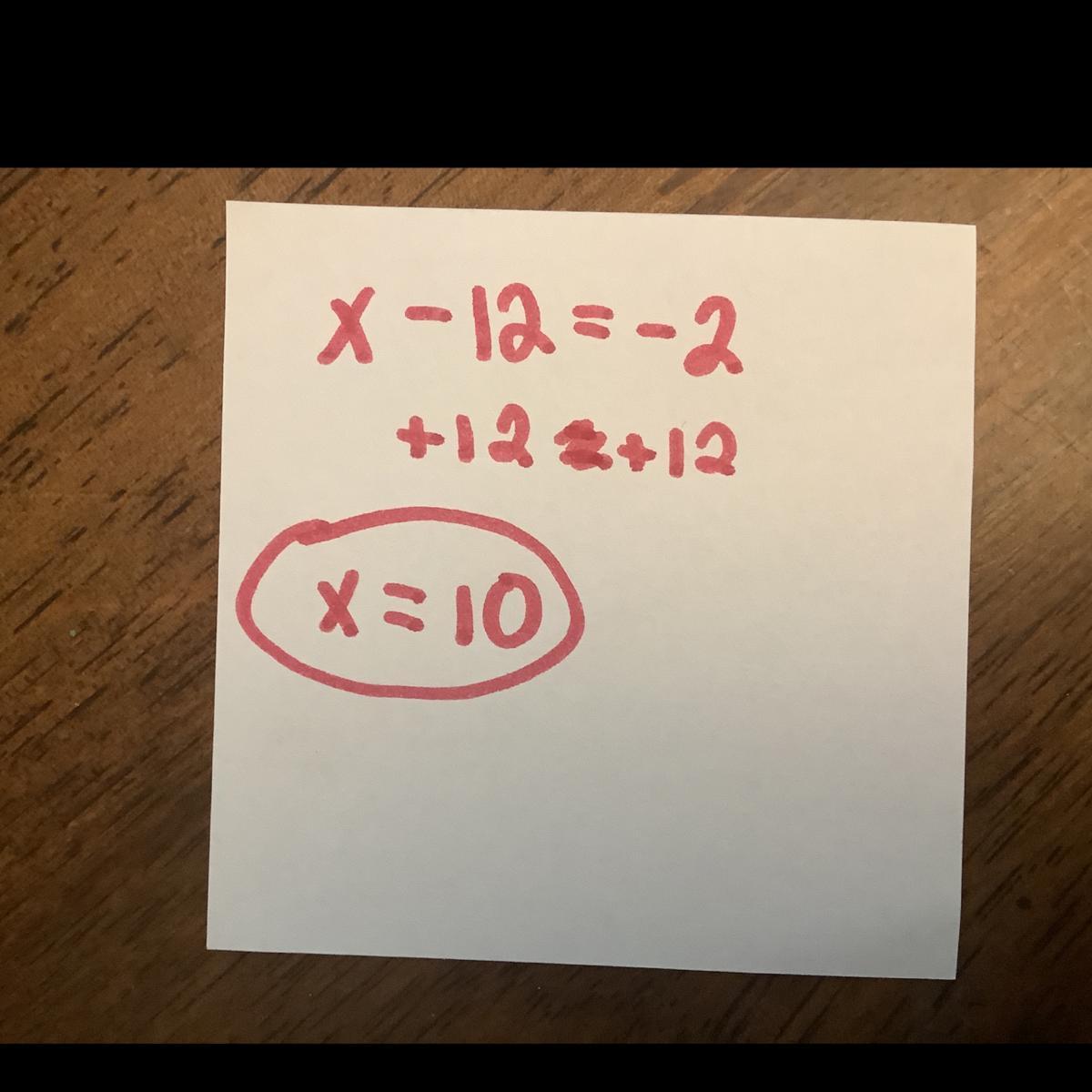what is the degrees of freedom for the critical value to test the significance of the regression coefficients using 0.05?
Answers
The degrees of freedom for the critical value to test the significance of the regression coefficients using 0.05 significance level depends on the sample size and the number of predictors in the model. Specifically, the degrees of freedom for the critical value is equal to the difference between the total sample size and the number of predictors.
For example, if we have a sample size of 150 and a model with 3 predictors, the degrees of freedom for the critical value would be 147 (150 - 3). This value is important because it is used to determine the critical t-value needed to reject the null hypothesis and conclude that the regression coefficient is statistically significant at the 0.05 significance level. In summary, the degrees of freedom for the critical value varies based on the sample size and number of predictors in the model.
To know more about freedom visit:
https://brainly.com/question/4077647
#SPJ11
Related Questions
a list of 20182018 positive integers has a unique mode, which occurs exactly 1010 times. what is the least number of distinct values that can occur in the list?
Answers
The least number of distinct values that can occur in the list is 225.
what is mode?The value that appears the most frequently in a data collection when it is unique is known as the mode, and like the median and mean, it can be used to measure central tendency. However, occasionally there is either no mode or more than one mode. When every observed value occurs exactly once in a data collection, there is no mode.
The mode appears 10 times. That leaves 2008 numbers.
The least number of distinct values will occur if all but one of the remaining values appears 9 times
= 2008/9
=223 1/9.
So, The list can include a maximum of 225 distinct values, with the mode appearing 10 times, 223 other values nine times, and the last value once.
Learn more about mode here:
https://brainly.com/question/28566521
#SPJ1
Answer this please I’m really struggling

Answers
Answer: x=10, y=7.5
Step-by-step explanation:
For this problem, we are given that BD bisects ABC. That means ABD and DBC are equal to each other. We are also given that ABC is 25. With the given information, we can create two equations.
Equation 1: 2x-y=3y-x
Equation 2: 2x-y+3y-x=25
Now, we can solve for x and y.
2x-y+3y-x=25 [combine like terms]
x+2y=25
Let's simplify Equation 1 by solving for a variable.
2x-y=3y-x [add both sides by x]
3x-y=3y [add both sides by y]
3x=4y [divide both sides by 3]
x=4/3y
Now that we have x, we can plug it into any equation to solve for y.
x+2y=25 [plug in x=4/3y]
(4/3y)+2y=25 [combine like terms]
10/3y=25 [multiply both sides by 3/10]
y=15/2
Now we can plug in y=15/2 to solve for x.
x=4/3y [plug in y=15/2]
x=4/3(15/2) [multiply]
x=10
Now, we know that x=10 and y=7.5.
The partial Factorization of X²-x-12 is modeled with algebra tiles. Which unit tiles are needed to complete the factorization? 3 negative unit tiles, 3 positive unit tiles, 4 negative unit tiles, 4 positive unit tiles

Answers
Answer: (c) 4 negative unit tiles
Step-by-step explanation:
Answer:
C. is the correct answer
Step-by-step explanation:
fred anderson, an artist, has recorded the number of visitors who visited his exhibit in the first 8 hours of opening day. he has made a scatter plot to depict the relationship between the number of hours and the number of visitors. how many visitors were there during the fourth hour? 1 21 4 20
Answers
Based on the given information, it is not possible to determine the exact number of visitors during the fourth hour.
The scatter plot created by Fred Anderson might provide a visual representation of the relationship between the number of hours and the number of visitors, but without the actual data points or additional information, we cannot determine the specific number of visitors during the fourth hour. To find the number of visitors during the fourth hour, we would need the corresponding data point or additional information from the scatter plot, such as the coordinates or a trend line equation. Without these details, it is not possible to determine the exact number of visitors during the fourth hour.
Learn more about visitors here
https://brainly.com/question/30984579
#SPJ11
solve the following system. 4x 2 9y 2 =72 x 2 - y 2 = 5 list your answers with the smallest x-values and then smallest y-value first.
Answers
To solve the system of equations:
4x^2 + 9y^2 = 72
x^2 - y^2 = 5
We can use the method of substitution. Let's solve the second equation for x^2:
x^2 = y^2 + 5
Now substitute x^2 in the first equation:
4(y^2 + 5) + 9y^2 = 72
4y^2 + 20 + 9y^2 = 72
13y^2 + 20 = 72
13y^2 = 52
y^2 = 4
y = ±2
Substituting y = 2 into x^2 = y^2 + 5, we get:
x^2 = 2^2 + 5
x^2 = 9
x = ±3
Therefore, the solutions to the system of equations are:
(x, y) = (-3, 2), (-3, -2), (3, 2), (3, -2)
Listing the solutions with the smallest x-values and then the smallest y-value first, we have:
(-3, -2), (-3, 2), (3, -2), (3, 2)
To learn more about equation click here:
brainly.com/question/9602029
#SPJ11
WILL GIVE BRAINLIEST!!! AND 75 POINTS

Answers
Answer:
A.2
hope it's helpful ❤❤❤❤❤❤
THANK YOU.
#

Answer:
\(\Large \boxed{2}\)
Step-by-step explanation:
\(\displaystyle \frac{14(2+3-2 \times 2)}{4^2-3^2}\)
Solve parenthesis
\(\displaystyle \frac{14 \times 1}{4^2-3^2}\)
Solve exponents
\(\displaystyle \frac{14}{7}=2\)
Pls help explain the graphs function things below! Asap!

Answers
Answer:
The graphs of the three functions A, B, and C are all different because they have different coefficients and signs in front of the absolute value function. Here is an explanation of the differences between the graphs:
A. f(x) = - |x|
This function is the opposite of the absolute value function. It takes the absolute value of x, and then multiplies the result by -1. This means that for any value of x, the output of the function is the negative of the absolute value of x. The graph of this function is a "V" shape that opens downward, with the vertex at the origin (0,0).
B. f(x) = 3/4 |x|
This function is a scaled version of the absolute value function. It takes the absolute value of x, and then multiplies the result by 3/4. This means that for any value of x, the output of the function is 3/4 of the absolute value of x. The graph of this function is a "V" shape that opens upward, with the vertex at the origin (0,0), and the slope of the arms of the "V" being less steep than the slope of the arms for the absolute value function.
C. f(x) = 4 |x|
This function is a scaled version of the absolute value function as well, but it has a different scale factor. It takes the absolute value of x, and then multiplies the result by 4. This means that for any value of x, the output of the function is 4 times the absolute value of x. The graph of this function is a "V" shape that opens upward, with the vertex at the origin (0,0), and the slope of the arms of the "V" being steeper than the slope of the arms for the absolute value function.
In summary, the graphs of these three functions are all "V" shapes, but they differ in terms of their orientation, their vertex location, and the steepness of the arms of the "V".
pls help need it ASAP will give brainlist

Answers
Answer:
BE = 3.5 m
Step-by-step explanation:
Δ ACB and Δ EDB are similar, so the ratios of corresponding sides are equal, that is
\(\frac{BE}{BA}\) = \(\frac{BD}{BC}\) , substitute values
\(\frac{BE}{21}\) = \(\frac{3}{18}\) ( cross- multiply )
18 BE = 63 ( divide both sides by 18 )
BE = 3.5
Victoria and Michael paid a $150 application deposit for an apartment. Their monthly rent is $2,200. They are required to provide a credit report that costs $35 and pay a security deposit equal to 1 month’s rent. The first and last month’s rent are due at the time of signing the lease. The broker charged 2.5% of the yearly rent. Find the cost to move in.
Answers
The cost to move in for Victoria and Michael is $7,645.
The cost to move into the apartment for Victoria and Michael can be found by calculating the sum of the application deposit, credit report cost, security deposit, first and last month's rent, and the broker fee.
Using the given information:
$150 is the application deposit
$35 is the cost of the credit report
Security deposit is 1 month's rent which is $2,200
First and last month's rent are also $2,200 each.
Thus, the total amount for these two months will be $4,400
The broker charged 2.5% of the yearly rent.
The yearly rent is $2,200 × 12 months = $26,400.
Therefore, the broker fee will be 2.5% of $26,400 which is $660.
Total cost to move in = $150 + $35 + $2,200 + $2,200 + $660 + $2,200 = $7,645
Therefore, the cost to move in for Victoria and Michael is $7,645.
for such more question on cost
https://brainly.com/question/25109150
#SPJ11
A survey was given to a random sample of 400 residents of a town to determine whether they support a new plan to raise taxes in order to increase education spending. Of those surveyed, 168 respondents said they were in favor of the plan. Determine a 95% confidence interval for the proportion of people who favor the tax plan, rounding values to the nearest thousandth.
Answers
The standard error of the sample proportion is sqrt[(0.42)(0.58)/400] = 0.032.
Using a 95% confidence level, the critical value is 1.96.
The margin of error is 1.96 * 0.032 = 0.063.
The 95% confidence interval is 0.42 ± 0.063, which is (0.357, 0.483).
Therefore, we can be 95% confident that the true proportion of people who favor the tax plan is between 0.357 and 0.483.
Escribe la expresión para "la diferencia de 10 y x".
Answers
Answer:
10-x=d
(d = diferencia de 10 y x)
solve for the indicated variable. e=f-g for g
Answers
Answer:
g = f - e
Step-by-step explanation:
f - g = e
- g = e - f
g. = f - e
please help!
find the equation (in terms of x) of the line through the point (-4,3) and (3,-2)

Answers
Answer: y= -5/7 x + 1/7
Step-by-step explanation:
Answer:
\(y=-\frac{5}{7} x+\frac{1}{7}\)
Step-by-step explanation:
Equation of a line: \(y = mx+b\)
m is the slope, and b is the y-intercept.
m = \(\frac{rise}{run} =\frac{y_{2}-y_{1} }{x_{2}-x_{1} } = \frac{-2-3}{3-(-4)} =-\frac{5}{7}\)
Now, we have \(y=-\frac{5}{7} x+b\)
We can insert one set of points in to solve for b.
We will use the first point (-4, 3):
\(3=-\frac{5}{7} (-4)+b\)
\(\frac{5}{7}* \:4+b=3\)
\(\frac{20}{7}+b=3\)
\(b=\frac{1}{7}\).
Equation:\(y=-\frac{5}{7} x+\frac{1}{7}\)
Solve and explain it clearly. 1. Use the substitution method to show that the solution of T(n) = T(n-1) + n is O(n^ 2 ). 2. Use a recursion tree to determine a good asymptotic upper bound on the recurrence T(n) = 2T(n-1) + 1. Use the substitution method to verify your answer.
Answers
We can conclude that T(n) = O(n²) for the recurrence relation T(n) = T(n-1) + n. We can conclude that T(n) = O(2ⁿ) is a valid upper bound for the recurrence relation T(n) = 2T(n-1) + 1.
1. To show that the solution of T(n) = T(n-1) + n is O(n²), we can use the substitution method. Let's assume that T(n) = O(n²). This means there exists a constant c and a positive integer k such that T(n) ≤ cn² for all n ≥ k.
Using the substitution method:
T(n) = T(n-1) + n
≤ c(n-1)² + n (by the assumption T(n-1) ≤ c(n-1)²)
= cn² - 2cn + c + n
≤ cn² - cn + n (for large values of n)
Now, we need to find values of c and k such that cn² - cn + n ≤ cn² for all n ≥ k. Choosing c = 2 and k = 1, we have:
2n² - n + n ≤ 2n² for all n ≥ 1
Therefore, we can conclude that T(n) = O(n²) for the recurrence relation T(n) = T(n-1) + n.
2. For the recurrence relation T(n) = 2T(n-1) + 1, let's use a recursion tree to determine an asymptotic upper bound. Starting with T(0) as the root, each node has two child nodes corresponding to T(n-1). Each node also has a constant cost of 1.
The height of the recursion tree is n, and at each level, the cost doubles. Therefore, the total cost of all levels in the tree is 2⁰ + 2¹ + 2 + ... + 2⁽ⁿ⁻¹⁾ = 2ⁿ - 1.
Hence, the asymptotic upper bound for T(n) is O(2ⁿ), as the cost increases exponentially with respect to n. Using the substitution method to verify this answer, let's assume T(n) = O(2ⁿ). This means there exists a constant c and a positive integer k such that T(n) ≤ c * 2ⁿ for all n ≥ k.
Using the substitution method:
T(n) = 2T(n-1) + 1
≤ 2(c * 2⁽ⁿ⁻¹⁾) + 1 (by the assumption T(n-1) ≤ c * 2⁽ⁿ⁻¹⁾)
= 2cn + 1
≤ c * 2ⁿ for large values of n
Thus, we can conclude that T(n) = O(2ⁿ) is a valid upper bound for the recurrence relation T(n) = 2T(n-1) + 1.
To know more about recurrence relation refer here:
https://brainly.com/question/32773332#
#SPJ11
1. Solve for the unknown in each triangle. Round each answer to the nearest tenth.

Answers
The values of the missing sides are;
a. x = 35. 6 degrees
b. x = 15
c. x = 22. 7 ft
d. x = 31. 7 degrees
How to determine the valuesTo determine the values, we have;
a. Using the tangent identity;
tan x = 5/7
Divide the values
tan x = 0. 7143
x = 35. 6 degrees
b. Using the Pythagorean theorem
x² = 9² + 12²
find the square
x² = 225
x = 15
c. Using the sine identity
sin 29= 11/x
cross multiply the values
x = 11/0. 4848
x = 22. 7 ft
d. sin x = 3.1/5.9
sin x = 0. 5254
x = 31. 7 degrees
Learn more about trigonometric identities at: https://brainly.com/question/7331447
#SPJ1
can someone help? i dont understand it really well

Answers
For a player to surpass Kareem Abdul-Jabbar, as the all-time score leader, he would need close to 40,000 points.
Based on the model, how many points would a player with a career total of 40,000 points have scored in their
rookie season? Explain how you determined your answer.

Answers
Based on the model, a player with a career total of 40,000 points would have scored 3,734 points in their rookie season.
How to construct and plot the data in a scatter plot?In this exercise, we would plot the rookie season-points on the x-axis (x-coordinates) of a scatter plot while the overall points would be plotted on the y-axis (y-coordinate) of the scatter plot through the use of Microsoft Excel.
On the Microsoft Excel worksheet, you should right click on any data point on the scatter plot, select format trend line, and then tick the box to display an equation of the curve of best fit (trend line) on the scatter plot.
Based on the scatter plot shown below, which models the relationship between the rookie season-points and the overall points, an equation of the curve of best fit is modeled as follows:
y = 5.74x + 18568
Based on the equation of the curve of best fit above, a player with a career total of 40,000 points would have scored the following points in their rookie season:
y = 5.74x + 18568
40,000 = 5.74x + 18568
5.74x = 40,000 - 18568
x = 21,432/5.74
x = 3,733.80 ≈ 3,734 points.
Read more on curve of best fit here: brainly.com/question/27311887
#SPJ1

What is the unit rate for 312 text messages sent per day (24 hours)
O 39 text messages per hour
O 7,488 messages per hour
1
26 text messages per hour
13 messages per hour

Answers
Combine Like Terms : 12x^4-2x+6x^4-10x
Answers
Let me know if you want more of an explanation.
solve t^2y'+2ty-y^3=0
Answers
The general solution to the given differential equation is
y = ± √(1 / (2ln|t| + 4/t - C2))
Solution to the differential equationTo solve the given differential equation, we can use the method of separable variables. Let's go through the steps:
Rearrange the equation to separate the variables:
t^2y' + 2ty - y^3 = 0
Divide both sides of the equation by t^2:
y' + (2y/t) - (y^3/t^2) = 0
Now, we can rewrite the equation as:
y' + (2y/t) = (y^3/t^2)
Separate the variables by moving the y-related terms to one side and the t-related terms to the other side:
(1/y^3)dy = (1/t - 2/t^2)dt
Integrate both sides of the equation:
∫(1/y^3)dy = ∫(1/t - 2/t^2)dt
To integrate the left side, let's use a substitution. Let u = y^(-2), then du = -2y^(-3)dy.
-1/2 ∫du = ∫(1/t - 2/t^2)dt
-1/2 u = ln|t| + 2/t + C1
-1/2 (y^(-2)) = ln|t| + 2/t + C1
Multiply through by -2:
y^(-2) = -2ln|t| - 4/t + C2
Now, take the reciprocal of both sides to solve for y:
y^2 = (-1) / (-2ln|t| - 4/t + C2)
y^2 = 1 / (2ln|t| + 4/t - C2)
Finally, taking the square root:
y = ± √(1 / (2ln|t| + 4/t - C2))
Therefore, the general solution to the given differential equation is:
y = ± √(1 / (2ln|t| + 4/t - C2))
Learn more on differential equation here https://brainly.com/question/1164377
#SPJ1
NEED HELP ASAP
A medication has a half-life of 4 hours after it enters the bloodstream. A nurse administers a dose of 500 milligrams to a patient at noon.
Only answer if you know pls!!
Find the amount of medication, in milligrams (mg), remaining in the patient's body at: (Round to the nearest 10th)
a. 3 p.m. on the same day:
b. 8 p.m. on the same day:
2. The expression 500 x (1/2)^5/4 represents the amount of medicine in the body sometime after it is administered. What is that time? (Make sure to signify am or pm)
Answers
1.
a.
mg remaining = (500) (1/2^(3/4)
= 297.3 mg
b.
mg remaining = (500)(1/2^(8/4))
= 125 mg
2.
5 represents the time elapsed from when the medication entered the bloodstream. Assuming the medication was given at noon, add 5 hours to have 5:00 pm.
Good luck! I need sleep. XD
Charles buys 30 packs of pens.
There are 15 pens in each pack.
Each pack costs £4.60.
Charles sells each pen for 80p but he only manages to sell 3/5 of the pens.
How much profit did he make?
Answers
Profit is equal to revenue - cost. So we need to find the difference of the money he takes in and the money he paid.
First, we find how much he paid.
Then, we find how much he made. Subtracting these two gives us the answer.
He paid for 30 packs of pens at $4.60 each, which amounts to $138.
He had a total of 450 pens and sold 3/5 of them. This means he sold 270 pens. He sold them for $0.80 each, meaning he made $216.
$216-$138 = $78
More work below

Simon (Mr. Lovett) completed 4 sets of chin-ups. Every set he reached a different prime number of chin-ups. Knowing this, what number of chin-ups could he have reached in each set?
Group of answer choices
Answers
Answer:
answer is b!
Step-by-step explanation:
hope this helps!!!
Calculate X+Y it in a row way 9
Answers
If you vertically compress the linear perent function, F(x) = x, by multiplying by 1\2
what is the equation of the new function?
Answers
Answer: \(y=\dfrac12 x\) .
Step-by-step explanation:
We know that \(a f (x)\) compresses f(x) vertically such that
if 0 < a < 1 (a fraction), the graph is compressed vertically by a factor of a units.if a > 1, the graph is stretched vertically by a factor of a units.If we vertically compress the linear parent function, F(x) = x, by multiplying by \(\dfrac12\).
Then, the equation of the new function is \(y=\dfrac12 F(x)=\dfrac12 x\) .
i.e. \(y=\dfrac12 x\) .
people drive an average of 12,000 miles per year with a standard deviation of 2,580 miles per year. what is the probability that a randomly selected sample of 36 drivers will drive, on average, more than 12,500 miles? does the central limit theorem apply? what is the sampling distribution of the mean?
Answers
The probability that a randomly selected sample of 36 drivers will drive, on average, more than 12,500 miles is approximately 0.123
This problem involves the sample mean of a set of data, and we can use the central limit theorem to approximate the distribution of sample means, even if the original distribution is not normal.
Let X be the number of miles driven by a single driver in a year. We know that the population mean µ = 12,000 miles and the population standard deviation σ = 2,580 miles. We also know that the sample size n = 36.
The sample mean X is an estimator of the population mean µ. The distribution of sample means is approximately normal with a mean of µ and a standard deviation of σ/√n, according to the central limit theorem
So, the distribution of sample means can be expressed as
X ~ N(µ, σ/√n)
Substituting the given values, we get
X ~ N(12,000, 2,580/√36) = N(12,000, 430)
Now we need to find the probability that a randomly selected sample of 36 drivers will drive, on average, more than 12,500 miles. This is equivalent to finding the probability that the sample mean is greater than 12,500
P(X > 12,500) = P(Z > (12,500 - 12,000) / 430)
where Z is a standard normal random variable.
P(Z > 1.16) = 1 - P(Z < 1.16) = 1 - 0.877 = 0.123
Learn more about probability here
brainly.com/question/11234923
#SPJ4
The given question is incomplete, the complete question is:
People drive an average of 12,000 miles per year with a standard deviation of 2,580 miles per year. what is the probability that a randomly selected sample of 36 drivers will drive, on average, more than 12,500 miles?
Suppose that x and y vary inversely, and x = 12 when y = 8 . Write the function that models the inverse variation.
Answers
Answer:
96/x
Step-by-step explanation:
When two variables x and y vary inversely, their product is a constant. Therefore, the function that models the inverse variation between x and y is:
x*y = k
where k is the constant of proportionality.
We can use the given information to find the value of k:
x = 12 when y = 8
so, k = xy = 128 = 96
Now we can use this value of k to write the function that models the inverse variation:
x*y = 96
To find the inverse variation, we divide both sides by y,
x = 96/y
Alternatively, we can write y = 96/x
So, the function that models the inverse variation between x and y is either x = 96/y or y = 96/x
: calculate the linear regression for the following points. plot the points and the linear regression line. (1, 1) (2, 3) (4, 5) (5, 4)
Answers
The linear regression for the given points is y = 0.7x + 0.9.
To calculate the linear regression, we need to find the equation of the line that best fits the given data points. The equation of a line is typically represented as y = mx + b, where m is the slope of the line and b is the y-intercept.
Let's calculate the slope, m, and the y-intercept, b, using the given data points (1, 1), (2, 3), (4, 5), and (5, 4).
Step 1: Calculate the mean values of x and y.
x bar = (1 + 2 + 4 + 5) / 4 = 3
y bar = (1 + 3 + 5 + 4) / 4 = 3.25
Step 2: Calculate the differences between each x-value and the mean of x (x - x bar) and the differences between each y-value and the mean of y (y - y bar).
(1 - 3) = -2
(2 - 3) = -1
(4 - 3) = 1
(5 - 3) = 2
(1 - 3.25) = -2.25
(3 - 3.25) = -0.25
(5 - 3.25) = 1.75
(4 - 3.25) = 0.75
Step 3: Calculate the sums of the products of the differences (x - x bar) and (y - y bar) and the sums of the squares of the differences (x - x bar)².
Σ((x - x bar)(y - y bar)) = (-2)(-2.25) + (-1)(-0.25) + (1)(1.75) + (2)(0.75) = 7.5
Σ((x - x bar)²) = (-2)² + (-1)² + (1)² + (2)² = 10
Step 4: Calculate the slope, m, using the formula:
m = Σ((x - x bar)(y - y bar)) / Σ((x - x bar)²) = 7.5 / 10 = 0.75
Step 5: Calculate the y-intercept, b, using the formula:
b = y bar - m * x bar = 3.25 - (0.75)(3) = 0.75
Therefore, the equation of the linear regression line is y = 0.75x + 0.75.
Now, we can plot the given points (1, 1), (2, 3), (4, 5), and (5, 4) on a graph and draw the linear regression line y = 0.75x + 0.75. The line will approximate the trend of the data points and show the relationship between x and y.
To learn more about linear regression, click here: brainly.com/question/30511665
#SPJ11
18 2 9 16 5 = 100 what are the arithmetical signs between theses numbers to make equations correct
Answers
The required equation to get the answer 100 following the BODMAS rule is (18 + 2) * 9 - (16 *5 ).
What is the BODMAS or PEDMAS rule?
Bracket, Of, Division, Multiplication, Addition, and Subtraction is referred to as BODMAS. A mathematical expression's order of execution is explained using the BODMAS. The acronym PEDMAS, which stands for Parentheses, Exponents, Division, Multiplication, Addition, and Subtraction, is sometimes used to refer to the BODMAS.
The brackets must be solved first, then powers or roots (i.e. of), Division, Multiplication, Addition, and finally Subtraction, according to the BODMAS rule. Any expression can only be solved correctly if the BODMAS rule or the PEDMAS rule is applied.
For this question, we use the trial and error method.
In this method, we apply arithmetic operators in different positions until we get the required answer.
We also follow the BODMAS rule
[(18 * 2) - 9 +16] / 5 = [96 - 9 + 16] /5 = [112 - 9] / 5 = 103/5 = 20.6
This is not the required answer, so we use another arrangement of operators.
(18 + 2) * 9 - (16 *5 ) = 20 * 9 - 80 = 180 - 80 = 100
Therefore the required equation to get the answer 100 is
(18 + 2) * 9 - (16 *5 ).
To learn more about BODMAS, follow the link.
https://brainly.com/question/29626868
#SPJ1
Does anyone know what this is :
x - 12 = -2
Answers
explanation is in the picture below.
Hope this helps!