What is the compound probability that student A chooses yellow and student B chooses yellow from their mnms at the same time? How likely is this? Yellow is worth 7/30
Answers
Step-by-step explanation:
yea................................
Related Questions
For the following LP, x2 and s1 are basic variables in the optimal tableau. Use the formulas of section 6.2 from your text book to determine the optimal tableau. max z = -X1 + X2 s.t. 2x1 + x2 = 4 x1 + x2 = 2 x1,x220
Answers
The optimal solution to the LP is x1 = 0, x2 = 2, with an optimal objective function value of 2.
To use the formulas from section 6.2 of the textbook to find the optimal tableau, we need to start with the initial feasible tableau, which has the following form:
Basis x1 x2 s1 s2 RHS
s1 2 1 1 0 4
s2 1 1 0 1 2
z -1 1 0 0 0
The first step is to identify the pivot element, which is the smallest positive ratio of the right-hand side (RHS) to the coefficient of the basic variable in each row. In this case, the ratios are:
s1: 4/2 = 2
s2: 2/1 = 2
Since both ratios are equal, we choose the variable with the smallest coefficient in the objective function as the entering variable. In this case, that is x1.
The second step is to perform the pivot operation, which involves dividing the pivot row by the pivot element and subtracting a suitable multiple of the pivot row from each of the other rows to eliminate the x1 variable from them. The result is a new tableau:
Basis x1 x2 s1 s2 RHS
s1 1 0 1/2 -1 2
x1 1 1 0 1 2
z 0 2 1 1 2
The new tableau shows that x2 and s1 are the basic variables in the optimal solution, with values of 2 and 2, respectively. The optimal value of the objective function is also shown in the tableau, which is 2.
Therefore, the optimal solution to the LP is x1 = 0, x2 = 2, with an optimal objective function value of 2.
Click the below link, to learn more about Optimal Solution:
https://brainly.com/question/15319802
#SPJ11
A bee colony produced 0.7 pounds of honey, but bears ate 0.2 pounds of it. How much honey remains?
Answers
The amount of honey remain left after bears ate 0.2 pounds of honey is equal to 0.5 pounds.
Amount of Honey produced by bee colony is equal to 0.7 pounds
Amount of honey consumed by bears is equal to 0.2 pounds
let 'x' be the amount of honey that remain left after bears consumed some amount of honey.
If a bee colony produced 0.7 pounds of honey, and bears ate 0.2 pounds of it,
Then the amount of honey that remains is represented by an equation,
x + 0.2pounds = 0.7 pounds
This implies,
⇒ x = 0.7 - 0.2
⇒ x = 0.5 pounds
Therefore, there are 0.5 pounds of honey remaining after the bears ate 0.2 pounds of it.
Learn more about pounds here
brainly.com/question/31314288
#SPJ1
Christmas tree lights are used not only for christmas trees, but sometimes to decorate college dorm rooms. Suppose that a string has 20 light bulbs. These lights are all wired in series, so that if one light bulb fails, the whole string fails. The probability that any one light fails is 0. 2. Each of the individual lights are independent of each other. What is the probability that the string will not fail?.
Answers
If a string has 20 light bulbs and these lights are all wired in series, so that if one light bulb fails, the whole string fails and the probability that any one light fails is 0.2 and each of the individual lights are independent of each other, then the probability that the string will not fail is 0.0115.
Probability in mathematics deals with the likelihood of an event to take place.
The probability that the string will not fail refers to when all 20 bulbs will not fail. As given in the conditions, each of the individual lights are independent of the other. Therefore;
the probability that any one of the lights will not fail is:
1 - probability that any one light fails = 1 - 0.2 = 0.8
And we need all 20 to be complete. The unity of events is a product of probabilities. Therefore the probability that the string will not fail is:
P = 0.8^20
P = 0.0115
Hence 0.0115 is the probability that the string will not fail.
To learn more about probability, click here:
https://brainly.com/question/251701
#SPJ4
Find the length of the missing side. Round to the nearest tenth. please help!!

Answers
16.1..BA
Evaluate the line integral by the two following methods.
xy dx + x2 dy
C is counterclockwise around the rectangle with vertices (0, 0), (5, 0), (5, 4), (0, 4).
(a) directly
(b) using Green's Theorem
Answers
For evaluating the line integral by the two following methods,
a. directly the value of the line integral is 62.5.
b. using Green's Theorem the value is also 62.5.
(a) Direct evaluation:
Parametrize the four sides of the rectangle C as follows:
The bottom side from (0,0) to (5,0): r(t) = <t, 0>, 0 ≤ t ≤ 5
The right side from (5,0) to (5,4): r(t) = <5, t>, 0 ≤ t ≤ 4
The top side from (5,4) to (0,4): r(t) = <t, 4>, 5 ≥ t ≥ 0
The left side from (0,4) to (0,0): r(t) = <0, t>, 4 ≥ t ≥ 0
Then we can evaluate the line integral as follows:
∫C xy dx + x² dy
= ∫[0,5] xy dt + ∫[0,4] 25 dt + ∫[5,0] 4x dt + ∫[4,0] 0 dt (by direct computation)
= 62.5
Therefore, the value of the line integral is 62.5.
(b) Evaluation using Green's Theorem:
Green's Theorem relates a line integral around a closed curve to a double integral over the region enclosed by the curve. Specifically, for a smooth vector field F = <P, Q> and a simple closed curve C that encloses a region D, Green's Theorem states that:
∫C P dx + Q dy = ∬D (∂Q/∂x - ∂P/∂y) dA
In this case, we have F = <y, x²>, and the region D is the rectangle enclosed by C.
We can apply Green's Theorem as follows:
∬D (∂Q/∂x - ∂P/∂y) dA
= ∬D (2x) dA
= 2 ∫[0,4] ∫[0,5] x dy dx
= 2 ∫[0,5] x [y]4_0 dx
= 62.5
Therefore, the value of the line integral using Green's Theorem is also 62.5, which matches the direct evaluation in part (a).
Learn more about the line integral at
https://brainly.com/question/30763905
#SPJ4
. suppose x is a normal random variable with mean 15.0 and standard deviation 1.25. calculate the following probabilities: (a) calculate p( | x – 15 | <= 3)
Answers
Probability that |x - 15| ≤ 3 is approximately 0.9772.
How to calculate p( | x – 15 | <= 3)?Given: x is a normal random variable with mean 15.0 and standard deviation 1.25.
We need to calculate: P(|x - 15| ≤ 3)
We know that |x - 15| represents the distance between the value of x and its mean, so we can rewrite the above expression as:
P(-3 ≤ x - 15 ≤ 3)
We can further simplify this by subtracting 15 from all terms:
P(-3 + 15 ≤ x ≤ 3 + 15)
P(12 ≤ x ≤ 18)
Now, we need to find the probability that x falls between 12 and 18. We can use the standard normal distribution by standardizing the values of x:
z1 = (12 - 15)/1.25 = -2.4
z2 = (18 - 15)/1.25 = 2.4
Using a standard normal distribution table or calculator, we can find the probability that z falls between -2.4 and 2.4:
P(-2.4 ≤ z ≤ 2.4) ≈ 0.9772
Therefore, the probability that |x - 15| ≤ 3 is approximately 0.9772.
Learn more about Probability.
brainly.com/question/30034780
#SPJ11
(3x-8)(2x+1) in simplest form
Answers
3x(2x+1)-8(2x+1)
6x²+3x-16x+16
6x²+13+16
Which of the following subsets of R^3×3 are subspaces of R^3×3
A. The invertible 3 × 3 matrices B. The 3 × 3 matrices with all zeros in the third row C. The 3 × 3 matrices in reduced row-echelon form D. The diagonal 3 × 3 matrices E. The 3 × 3 matrices with trace (the trace of a matrix is the sum of its diagonal entries)
F. The 3 x 3 matrices of
Answers
The subspaces of R^3x3 are: B. The invertible 3x3 matrices, C. The 3x3 matrices with all zeros in the third row, D. The diagonal 3x3 matrices, and F. The 3x3 matrices of rank 1.
A subspace of R^3x3 is a subset that satisfies three conditions: it contains the zero matrix, it is closed under matrix addition, and it is closed under scalar multiplication.
B. The invertible 3x3 matrices form a subspace because the zero matrix is invertible and any linear combination or product of invertible matrices is also invertible.
C. The 3x3 matrices with all zeros in the third row form a subspace. Adding two matrices with all zeros in the third row results in a matrix with all zeros in the third row, and multiplying a matrix with all zeros in the third row by a scalar also yields a matrix with all zeros in the third row.
D. The diagonal 3x3 matrices form a subspace because the sum of two diagonal matrices is still a diagonal matrix, and scaling a diagonal matrix by a scalar preserves its diagonal structure.
E. The 3x3 matrices with a specific trace value do not form a subspace because the sum of two matrices with different trace values will generally not have the same trace.
F. The 3x3 matrices of rank 1 do form a subspace. The zero matrix is of rank 0, and any linear combination of rank 1 matrices will also have rank 1. Furthermore, scaling a rank 1 matrix by a scalar preserves its rank.
Learn more about zero matrix here: https://brainly.com/question/31039102
#SPJ11
which graph of ordered pais shows a proportional relationship? i need help lol
Answers
Find the unit rate of the equation:
Y=25x
Answers
Answer:
I think the answer is 12 mph
Please solve the attached problem with all steps.
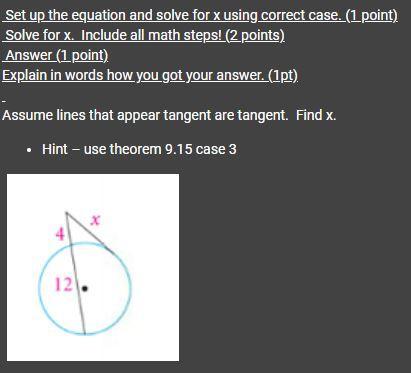
Answers
Answer:
x = 8
Step-by-step explanation:
Theorem
When a secant segment and a tangent segment meet at an exterior point, the square of the measure of the tangent segment is equal to the product of the measures of the secant segment and its external secant segment.
Secant: a straight line that intersects a circle at two points
Tangent: a straight line that touches a circle at only one point
Given:
tangent segment = xsecant segment = 4 + 12 = 16external secant segment = 4⇒ x² = 16 · 4
⇒ x² = 64
⇒ x² = √(64)
⇒ x = ±8
As distance is positive, x = 8
SV bisects angle RST. if m angle RST = 62, what is m angle RSV?
Answers
See attachment for math work and answer.

The measure of ∠RSV is 31°.
Given that, SV bisects ∠RST=62°.
We need to find the value of m∠RSV.
What is an angle bisector?The angle bisector in geometry is the ray, line, or segment which divides a given angle into two equal parts. For example, an angle bisector of a 60-degree angle will divide it into two angles of 30 degrees each. In other words, it divides an angle into two smaller congruent angles.
Since SV bisects ∠RST into equal parts.
That is, ∠RSV=∠TSV
So, ∠RST=∠RSV+∠TSV
⇒∠RST=2∠RSV
⇒62°=2∠RSV
⇒∠RSV=31°
Therefore, the measure of ∠RSV is 31°.
To learn more about an angle bisector visit:
brainly.com/question/12896755.
#SPJ2

Will mark brainliest to the best answer!
Sequence: 1,3,15,61,213
Find the 6th term.
Find the nth term.

Answers
Answer:
687
Step-by-step explanation:

The sixth term and the nth term in the sequence will be:
6th term: 13, 26, 42, 729,
nth term: 2n + 1, n², n² + n, 3ⁿ
How to illustrate the sequence?The sixth term and the nth term will be calculated thus:
6th term = a + (n - 1)d
= 3 + (6 - 1)2
= 3 + 10
= 13
Here, the 6th term: 13, 26, 42, 729,
Also the nth term. will be 2n + 1, n², n² + n, 3ⁿ
Learn more about sequence on:
brainly.com/question/6561461
#SPJ1
Under what circumstances can arithmetic expressions be used as
control
expressions?
Answers
Arithmetic expressions can be used as control expressions in programming languages when a control structure, such as an if statement or a loop, expects a condition to determine the flow of execution
Arithmetic expressions can be used as control expressions in certain programming languages or contexts where a control structure expects a conditional expression to determine the flow of execution.
Typically, control expressions are used in decision-making structures such as if statements, while loops, for loops, and switch statements.
In most programming languages, the control expression must evaluate to a boolean value (true or false) in order to determine the execution path. However, some languages allow arithmetic expressions to be used in control structures, considering a value of zero as false and any non-zero value as true.
To learn more on Arithmetic expressions click:
https://brainly.com/question/17722547
#SPJ4
April is going to the bakery to purchase donuts and cinnamon rolls for the office personnel. She must purchase at least 30 items. She has collected only $30, so total cost must be no more than $30. If d represents donuts that cost $0.75 each and r represents cinnamon rolls that cost $1.25 each, which system of inequalities can be used to represent the region for the number of donuts and cinnamon rolls April could purchase
Answers
Answer:
d + r ≥ 30
$0.75d + $1.25r ≤ $30
Step-by-step explanation:
Given the following :
Number of items to purchase = atleast 30
Total cost must be no more than 30
cost of donut (d) = $0.75
Cost of cinnamon (r) = $1.25
Number of donuts and cinnamon to purchase
To total number of items :
Donut + cinnamon ≥ 30
d + r ≥ 30
Cost of items to purchase :
Cost = price per item * number of items
$0.75d + $1.25r ≤ $30
Find the value of a5, given the sequence defined as: a1 = 32 an = (1/2)an-1
Answers
Answer:
a5 = 2
Step-by-step explanation:
If a1 = 32,
a1 = 1/2 a0 = 32
a0 = 64
With that, we know that
a0 = 64,
a1 = 32
so, a2 is definitely 16. From that, we may know the formula,
an = a0 (1/2)^n
a5 = a0 (1/2)^5
a5 = 64 (1/32)
a5 = 2
for the orthogonal matrix verify that (ax ay)=(x y)
Answers
The given statement "If A is n × n an orthogonal. Then for all X, Y ∈ Rₙ we have AX · AY = X · Y" is proved.
Given that A is a n * n order matrix.
And X, Y ∈ Rₙ so,
|X - Y|² = (X - Y) * (X - Y)
|X - Y|² = |X|² - 2 * X * Y + |Y|²
2 * X * Y = |X|² + |Y|² - |X - Y|²
Since A is orthogonal matrix so,
2 * (AX * AY) = |AX|² + |AY|² - |AX - AY|²
2 * (AX * AY) = |X|² + |Y|² - |X - Y|²
2 * (AX * AY) = 2 * X * Y
(AX * AY) = X * Y
Hence the statement is proved.
To know more about orthogonal matrix here
https://brainly.com/question/30426447
#SPJ4
The question is incomplete. The complete question will be -
"Suppose that A is n × n an orthogonal. Then for all X, Y ∈ Rₙ we have
AX · AY = X · Y"
What is the relation between the sine and cosine values of angles in each quadrant? How would you use the 60° angle to find sine and cosine of 120°, 240°, and 300°? What angles could we find sine and cosine for using information for π/4 and π/6?
Answers
The angles, 60°, \(\displaystyle \frac{\pi}{4}\) and \(\displaystyle \frac{\pi}{6}\) are special angles that have known trigonometric ratio values.
First part;
The sine and cosine gives the coordinates of the tip of the radius of a unit circle as it rotates P(cos(θ), sin(θ))Second part;
With the knowledge of the sine and cosine of 60°, we have; sin(60°) = sin(120°), sin(240°) = -sin(60°), sin(300°) = -sin(60°)cos(120°) = -cos(60°), cos(240°) = -cos(60°), cos(300°) = cos(60°)Third part;
\(\displaystyle \frac{\pi}{4}\) can be used to find the sine and cosine of \(\displaystyle \frac{3 \cdot \pi}{4}\), \(\displaystyle \frac{5 \cdot \pi}{4}\), and \(\displaystyle \frac{7 \cdot \pi}{4}\) \(\displaystyle \frac{\pi}{6}\), can be used to find the sine and cosine of \(\displaystyle \frac{5 \cdot \pi}{6}\), \(\displaystyle \frac{7 \cdot \pi}{6}\), and \(\displaystyle \frac{11 \cdot \pi}{6}\)Reasons:
First Part;
Considering a unit circle with the center at the origin of the graph, we have;
The sine of the angle, θ, rotated by the radius is the vertical distance of a point P on the circle which is the location of the radius, from the horizontal axis.
The cosine of the angle, θ, is the horizontal distance of P from the vertical axis, such that we have;
The coordinates of point P = (cos(θ), sin(θ))
In the four quadrant, we have;
First Quadrant; All trigonometric ratios are positive
Second Quadrant; sine is positive
Third Quadrant; Tan is positive
Fourth Quadrant; Cosine is positive
Second part;
We have; At 120°, the point P is the same elevation from the horizontal axis, therefore;
sin(60°) = sin(120°) = 0.5·√3
However, the x-coordinate of the point P is in the negative direction, therefore, we get;
cos(120°) = -cos(60°) = -0.5
Similarly from the quadrant relationship, we have;
240° is in the third quadrant, and it is 60° below the negative horizontal line, therefore;
sin(240°) = -sin(60°) = -0.5·√3
cos(240°) = -cos(60°) = -0.5
300° is in the fourth quadrant, and it is 60° below the positive x-axis, therefore;
sin(300°) is negative and cos(300°) is positive
Which gives;
sin(300°) = -sin(60°) = -0.5·√3
cos(300°) = cos(60°) = 0.5
Third part;
\(\displaystyle \frac{\pi}{4} =45^{\circ}\)
\(\displaystyle \frac{\pi}{6} =30^{\circ}\)
The sine and cosine of 45° can be used to find the sine and cosine of (180° + 45°) = 225°, (360° - 45°) = 315°
Also, due to the mid location of the angle 45° on the quadrant, we have;
Another angles is the sines and cosine of (90° + 45°) = 135°
Therefore, \(\displaystyle \frac{\pi}{4}\), can be used to find the sine and cosine of 135°, 225°, and 315°
\(\displaystyle 135^{\circ} = \mathbf{\frac{3 \cdot \pi}{4}}\), \(\displaystyle 225^{\circ} = \frac{5 \cdot \pi}{4}\), \(\displaystyle 315^{\circ} = \frac{7 \cdot \pi}{4}\)
Therefore,
\(\displaystyle \frac{\pi}{4}\) can be used to find the sine and cosine of \(\displaystyle \mathbf{\frac{3 \cdot \pi}{4}}\), \(\displaystyle \mathbf{\frac{5 \cdot \pi}{4}}\), and \(\displaystyle \mathbf{ \frac{7 \cdot \pi}{4}}\)
Similarly, the sine and cosine of, \(\displaystyle \frac{\pi}{6}\) = 30° can be used to find the sine and cosine of 150°, 210°, and 330°.
\(\displaystyle 150^{\circ} = \frac{5 \cdot \pi}{6}\), \(\displaystyle 210^{\circ} = \frac{7 \cdot \pi}{6}\), and \(\displaystyle 330^{\circ} = \frac{11 \cdot \pi}{6}\)
\(\displaystyle \frac{\pi}{6}\), can be used to find the sine and cosine of \(\displaystyle \mathbf{ \frac{5 \cdot \pi}{6}}\), \(\displaystyle \mathbf{ \frac{7 \cdot \pi}{6}}\), and \(\displaystyle \mathbf{\frac{11 \cdot \pi}{6}}\)
Learn more about the sine and cosine of angles here:
https://brainly.com/question/4372174
Answer:
Step-by-step explanation:
The cosine value of an angle is the x coordinate of the point the angle corresponds to on the unit circle, and the sine value of an angle is the y coordinate of that point. 120, 240, and 300 all form 60 degree reference angles which in turn forms 30-60-90 triangles which help to find the sine and cosine of these corresponding angles. Pi/4 radians converts to 45 degrees which forms a 45-45-90 special triangle on the unit circle which has its own known trigonometric ratio. Pi/6 radians converts to 30 degrees which forms a 30-60-90 triangle on the unit circle which also has a known trigonometric ratio. These ratios help find the sine and cosine of the angles on the unit circle which corresponds to a point on the coordinate plane.
Consider the Fourier series for the periodic function: z(t) = cos(6t) + sin(8t) + et The Fourier coefficient C of the exponential series is:
Answers
The Fourier coefficient C of the exponential series for the periodic function z(t) = cos(6t) + sin(8t) + et is zero.
To find the Fourier coefficient C of the exponential series for the periodic function z(t) = cos(6t) + sin(8t) + et, we need to compute the integral of the product of z(t) and the complex conjugate of the complex exponential function \(e^{-jwt\) over one period.
The Fourier coefficient C is given by the formula:
C = (1/To) * ∫[0,To] z(t) * \(e^{-jwt\) dt
In this case, the periodic function z(t) includes an exponential term, so we need to compute the integral for both the sinusoidal terms (cos(6t) and sin(8t)) and the exponential term (et) separately.
Let's start with the exponential term:
\(C_{exponential\) = (1/To) * ∫[0,To] et * \(e^{-jwt\) dt
Since the function et is not periodic, the integral over one period To will not result in a finite value. Therefore, the Fourier coefficient \(C_{exponential\) for the exponential term will be zero.
Now, let's compute the Fourier coefficients for the sinusoidal terms:
\(C_{cosine\) = (1/To) * ∫[0,To] cos(6t) * \(e^{-jwt\) dt
\(C_{sine\) = (1/To) * ∫[0,To] sin(8t) * \(e^{-jwt\) dt
To evaluate these integrals, we need to know the specific value of ω. Without this information, we cannot determine the exact values of \(C_{cosine\) and \(C_{sine\). The Fourier coefficients of the sinusoidal terms will depend on the frequency content of the function z(t).
In summary, the Fourier coefficient C of the exponential series for the periodic function z(t) = cos(6t) + sin(8t) + et is zero (\(C_{exponential\) = 0), while the Fourier coefficients of the sinusoidal terms (\(C_{cosine\) and \(C_{sine\)) cannot be determined without specifying the frequency ω.
To learn more about coefficient here:
https://brainly.com/question/30215548
#SPJ4
A train traveling at 40 mph can go 15 more miles in the same amount of time that a car can traveling at 30 mph can go. How far does the train go in the same amount of time?
Answers
Answer:
60
Step-by-step explanation:
After 1.5 hour the train travel 60 mille (1.5 × 40) and the car travel 45 (1.5 × 30) which make the train travel 15 more than the car at the same amount of time.
3. Boynton Beach recreation center has collected a total of 510 donated tickets for free ice
cones. Beginning on the second day of summer vacation, the recreation center randomly
selects 9 children to each receive one of the free ice cream tickets. Assuming the
recreation center continues this pattern of giving away tickets to 9 children each day,
which explicit formula shows the
number of ice cone tickets remaining at the end of the
day, after n number of days?
a.=510-9n
B.=510+9(n-1)
C.510-9(n-1)
D.9(n-1)-510
Answers
Answer:
Hence, in this case, it is concluded that the correct answer is "N = 618 - n x 7"
Step-by-step explanation:
Considering the situation described above, the explicit formula that shows the number of ice cream tickets remaining at the end of the day, after n number of days is "N = 618 - n x 7."
This is based on the idea that each day of the ice cream ticket is defined as 7 tickets taken.
Thus the ticket listing for each day is described as
Day 1. 618 - 7 OR 618 - 1 × 7;
Day 2. 618 - 14 OR. 618 - 2 × 7;
Day 3. 618 - 21 OR 618 - 3 × 7;
Therefore, from this illustration above, the formula needed is: "N = 618 - n x 7."
What is the value of 8 in 0.283
Answers
Answer:
0.08 which is eight hundredths
Step-by-step explanation:
0.283
The 8 in is the hundredths place, so the eight's value is 8 hundredths.
Answer:
the value of 8 is hundredths
Jaon went hopping
He bought a watch and a pair of trainer for a total price of £53. 55
Thi price include a 15% loyalty dicount
Before the dicount, the trainer were priced at £38
Work out the price of the watch before the dicount
Answers
The price of the watch before the discount is calculated to be £24.44.
As the total price of the watch and a pair of trainers is £53. 55 and the price of the trainer before the discount was £38, we first calculate the price of the trainers after the discount as follows;
discount on a pair of trainers = 15/100 × 38 = £5.7
cost of trainers after discount = £38 - 5.7 = £32.3
Now the price of the watch after the discount can be calculated by subtraction as follows;
price of watch after discount = total price - price of trainers after discount
price of watch after discount = £53. 55 - £32.3
price of watch after discount = £21.25
Now the price of the watch before the discount can be calculated as follows;
price of watch before discount = £21.25 × 15/100
price of watch before discount = £21.25 + £3.1875
price of watch before discount = £24.44
To learn more about subtraction; click here:
https://brainly.com/question/13378503
#SPJ4
find a set of parametric equations for the rectangular equation that satisfies the given condition. (enter your answers as a comma-separated list.)y = 3x − 2, t = 0 at the point (2, 4)
Answers
The set of parametric equations for the line y = 3x - 2, with t = 0 at the point (2,4), is x = t + 2, y = 3t + 4.
We can use the point-slope form of a line to find the parametric equations:
y - y1 = m(x - x1), where (x1, y1) is the given point and m is the slope of the line.
The slope of the line y = 3x - 2 is 3, so we have:
y - 4 = 3(x - 2)
Simplifying, we get:
y = 3x - 2
We can rewrite this as a set of parametric equations:
x = t + 2
y = 3t + 4
So the set of parametric equations for the line y = 3x - 2, with t = 0 at the point (2,4), is:
x = t + 2, y = 3t + 4.
Learn more about parametric equations here
https://brainly.com/question/30451972
#SPJ11
Belief in Haunted Places A random sample of 340 college students were asked if they believed that places could be haunted, and 133 responded yes. Estimate the true proportion of college students who believe in the possibility of haunted places with 95% confidence. According to Time magazine, 37% of Americans believe that places can be haunted. Round intermediate and final answers to at least three decimal places.
Answers
According to the given data, a random sample of 340 college students were asked if they believed that places could be haunted, and 133 responded yes.
The aim is to estimate the true proportion of college students who believe in the possibility of haunted places with 95% confidence. Also, it is given that according to Time magazine, 37% of Americans believe that places can be haunted.
The point estimate for the true proportion is:
P-hat = x/
nowhere x is the number of students who believe in the possibility of haunted places and n is the sample size.= 133/340
= 0.3912
The standard error of P-hat is:
\(SE = sqrt{[P-hat(1 - P-hat)]/n}SE
= sqrt{[0.3912(1 - 0.3912)]/340}SE
= 0.0307\)
The margin of error for a 95% confidence interval is:
ME = z*SE
where z is the z-score associated with 95% confidence level. Since the sample size is greater than 30, we can use the standard normal distribution and look up the z-value using a z-table or calculator.
For a 95% confidence level, the z-value is 1.96.
ME = 1.96 * 0.0307ME = 0.0601
The 95% confidence interval is:
P-hat ± ME0.3912 ± 0.0601
The lower limit is 0.3311 and the upper limit is 0.4513.
Thus, we can estimate with 95% confidence that the true proportion of college students who believe in the possibility of haunted places is between 0.3311 and 0.4513.
To know more about college visit:
https://brainly.com/question/16942544
#SPJ11
find the area and perimeter of the figures

Answers
Answer:
6x+6 or 4x+10
Step-by-step explanation:
hope u like it
Answer:
a) 196cm^2
b) 225cm^2
c) 180 cm^2
Step-by-step explanation:
a) The figure is a square, so you can use the formula: a = l^2, or area equals length of one side squared.
a = (14cm)^2
a = 196cm^2
b) a = (15cm)^2
a = 225cm^2
c) This one is a parallelogram, so it's trickier. However, we can imagine the figure as a rectangle by taking the small triangle that sticks out on the right and putting it into the gap in the left. Now, we can solve this using the formula for a rectangle: a = l x w.
a = l x w
a = 18cm x 10 cm = 180 cm^2
:)
Solve for x: -243 = -9(10 + x)
Answers
Answer:
x=17
Step-by-step explanation:
−243=−9(10+x)
Step 1: Simplify both sides of the equation.
−243=−9(10+x)
−243=(−9)(10)+(−9)(x)(Distribute)
−243=−90+−9x
−243=−9x−90
Step 2: Flip the equation.
−9x−90=−243
Step 3: Add 90 to both sides.
−9x−90+90=−243+90
−9x=−153
Step 4: Divide both sides by -9.
−9x/−9
= −153/−9
x=17
Answer:
x=17
Step-by-step explanation:
I took the test!
If a 50-year flood occurs on the Mississippi River in 2020, what is the probability that a flood of the same magnitude will occur in 2021
Answers
The probability of a flood of the same magnitude, specifically a 50-year flood, occurring in 2021 would still be 2%.
The occurrence of a flood with a certain magnitude, such as a 50-year flood, is based on the concept of return periods. A 50-year flood refers to a flood event that has a 2% (1 in 50) chance of occurring in any given year.
It's important to note that the probability of a flood of the same magnitude occurring in the following year is independent of the previous flood event.
The fact that a 50-year flood occurred in 2020 does not affect the probability of a similar flood occurring in 2021.
The term "50-year flood" refers to a flood that has a 2% chance of occurring in any given year. It does not mean that a flood of the same magnitude will occur exactly every 50 years. Each year is independent of the previous year in terms of flood occurrence, and the probability remains the same each year.
A important to note that flood probabilities can change over time due to factors such as climate change, land use changes, and other environmental factors. Therefore, it's essential to regularly update flood probability assessments using the most recent data and analysis techniques.
To know more about probability here
https://brainly.com/question/30034780
#SPJ4
Complete question:
If a 50-year flood occurs on the Mississippi River in 2020 .what is the chance that a flood of the same magnitude will occurs in the year 2021?
There are 30 birds in an enclosure at the zoo. 1/5 of the birds are native to North America. 1/3 of the birds are native to South America. The remaining birds are native to Australla. How many of the birds in the enclosure are Native to Australla? Plz helppppppppp
Answers
Answer:
Number of Australia birds = 14
Step-by-step explanation:
Given:
Total number of birds = 30
North america birds = 1/5 birds = 30/5 = 6 birds
South america birds = 1/3 birds = 30/3 = 10 birds
Find:
Number of Australia birds
Computation:
Number of Australia birds = Total number of birds - North america birds - South america birds
Number of Australia birds = 30 - 6 - 10
Number of Australia birds = 14
Can someone help please?

Answers
Answer:
Step-by-step explanation:
2. 30 minutes
3. 985 years
4. 75 degrees
5. -5 degrees
6. 30340 feet
7. 49 degrees