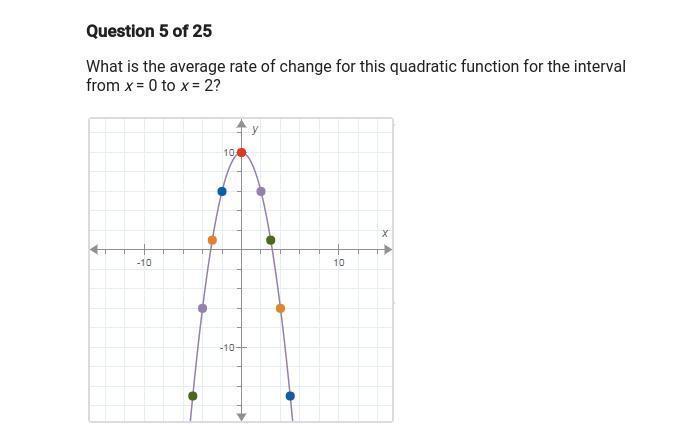
What is the average rate of change of the function from x = 0 to x = 2?.

Answer:

Step-by-step explanation:

It’s A

The measure of the arc ADC is 252°

The arc of a circle is defined as the part or segment of the circumference of a circle.

Given that, a circle O, with tangents AB and BC, the measure of arc AC is 108°, the measure of angle ABC is 72°, we need to find the measure of arc ADC,

According to the definition of circle,

We have,

m ∠ABC = (m arc ADC + m arc ADC) / 2

72° = (m arc ADC - 108°) / 2

144° = m arc ADC - 108°

m arc ADC = 144° + 108°

m arc ADC = 252°

Hence the measure of the arc ADC is 252°

Learn more about arcs, click;

https://brainly.com/question/18741430

#SPJ5

Answer:

\(m\angle 1=95^{\circ}\)

Step-by-step explanation:

If we drew an auxiliary line parallel to line \(p\) and line \(q\) that intersects the vertex of \(\angle 1\), we would form three angles, one of them being

The largest of these angles corresponds with the angle marked as \(148^{\circ}\).

The angle on the bottom right corresponds with the angle next to the one marked as \(63^{\circ}\). Therefore, its measure is \(180-63=117^{\circ}\).

Since there are \(360^{\circ}\) in a circle, we can now write the following equation:

\(m\angle 1+117+148=360,\\m\angle 1=\fbox{$95^{\circ}\checkmark$}\).

Answer:

95

Step-by-step explanation:

The way SkiffMacKinaw did this problem is the way it should be done. There is another way of doing it by extending both arms of <1 until they intersect p and q and solve the triangle hanging from p.

You then find the the angles of the triangle. The vertex angle is the supplement to <1.

This method works but it is not nearly as elegant as the original answer. This is one of the best awarded Brainliests I've seen lately.

Answer:

the answer to your question is line 6

Step-by-step explanation:

hope this helps

a. The truck rental cost when you drive 85 miles is  $85.7.

b. The number of miles driven when the cost is $65.96 is 0.42x.

a. To find the truck rental cost when driving 85 miles, we can substitute the value of x into the given function.

f(x) = 0.42x + 50

Substituting x = 85:

f(85) = 0.42(85) + 50

= 35.7 + 50

= 85.7

Therefore, the truck rental cost when driving 85 miles is $85.70.

b. To determine the number of miles driven when the cost is $65.96, we can set up an equation using the given function.

f(x) = 0.42x + 50

Substituting f(x) = 65.96:

65.96 = 0.42x + 50

Subtracting 50 from both sides:

65.96 - 50 = 0.42x

15.96 = 0.42x

To isolate x, we divide both sides by 0.42:

15.96 / 0.42 = x

38 = x

Therefore, the number of miles driven when the cost is $65.96 is 38 miles.

In summary, when driving 85 miles, the truck rental cost is $85.70, and when the cost is $65.96, the number of miles driven is 38 miles.

For similar question on equation.

https://brainly.com/question/25976025

#SPJ8

Two steps that will complete the list correctly are:

4. The original measurement should be multiplied by the conversion factors.

5. Verify that it makes sense.

A conversion factor can be used to switch from one set of units to another by multiplying or dividing a number. When a conversion is necessary, the appropriate conversion factor to an equivalent value must be applied.

Let's use an example of converting from inches to centimeters to address this query.

10 inches should be converted to cm.

To know more about units, visit:

https://brainly.com/question/18522397

#SPJ4

Therefore, the projectile goes approximately 6.9 × 10^6 meters or 6,900 kilometers high.

Let's first convert the initial speed from km/hr to m/s to be consistent with the unit of acceleration due to gravity.

1.30×10^4 km/hr = (1.30×10^4 × 1000 m/km) / (3600 s/hr) = 3611.11 m/s

We can use the kinematic equation: Δy = v0t + 1/2at^2 to determine the maximum height reached by the projectile. At the highest point, the velocity is zero, so we can use the fact that v = v0 + at = 0 to find the time it takes to reach the maximum height.

v0 = 3611.11 m/s (initial velocity)

a = -9.81 m/s^2 (acceleration due to gravity)

t = -v0/a = -3611.11/(-9.81) = 367.97 s (time to reach maximum height)

Now we can use the time to find the maximum height reached:

Δy = v0t + 1/2at^2 = 3611.11 × 367.97 + 1/2 × (-9.81) × (367.97)^2 ≈ 6.9 × 10^6 meters

To know more about projectile,

https://brainly.com/question/6848934

#SPJ11

The clerk walked approximately 0.371π meters during the 132 minutes of delivering along the hallway.

To find the number of 3-meter segments the clerk walked during the 132 minutes, we need to integrate the velocity function over the given time interval.

v(t) = 4π sin(t)

The clerk starts at one end and takes 13 minutes to finish deliveries, so the time interval is from t = 0 to t = 13.

To calculate the distance walked, we integrate the absolute value of the velocity function over the given interval:

Distance = ∫[0, 13] |v(t)| dt

Let's calculate the integral:

Distance = ∫[0, 13] |4π sin(t)| dt

Since the absolute value of sin(t) is positive for the given interval, we can simplify the integral to:

Distance = 4π ∫[0, 13] sin(t) dt

Using the integral of sin(t), which is -cos(t), the expression becomes:

Distance = -4π cos(t) |[0, 13]

Now we can evaluate the integral over the given interval:

Distance = -4π (cos(13) - cos(0))

Simplifying further:

Distance = -4π (cos(13) - 1)

Calculating the value:

Distance ≈ -4π (0.907 - 1)

Distance ≈ -4π (-0.093)

Distance ≈ 0.371π meters

Therefore, the clerk walked approximately 0.371π meters during the 132 minutes.

To learn more about velocity function visit : https://brainly.com/question/25749514

#SPJ11

The value of the (f⁻¹)'(1) = -3/4.


To find (f⁻¹)'(1), we use the chain rule. The chain rule states that, for a function y = f(g(x)), then y' = f'(g(x))*g'(x). In our case, y is f⁻¹ and g is f.

Therefore,
(f⁻¹)'(1) = f'(f⁻¹(1)) * (f⁻¹)'(1). We are given

f(-3) = 1, f(1) = -4, f'(-3) = 4, and f'(-4) = -3.

Therefore, we can solve for (f⁻¹)'(1). We start by solving for f⁻¹(1). We know that f(1) = -4, so f⁻¹(1) = -4.

Plugging this into our equation, we get (f⁻¹)'(1) = f'(-4)*(f⁻¹)'(1).

We are given f'(-4) = -3,

so (f⁻¹)'(1) = (-3)*(f⁻¹)'(1).

Solving this equation, we get (f⁻¹)'(1) = -3/4.

To know more about chain rule click on below link:

https://brainly.com/question/28972262#

#SPJ11

Answer:

Step-by-step explanation:

Life in the mid-1800s was marked by widespread prejudice and discrimination against minority groups, including immigrants and African Americans. The period was also characterized by a series of famines that led to significant suffering and mortality. Nativist movements gained popularity, promoting the interests of those born in the United States over those of immigrants. At the same time, millions of emigrants left their homes in search of better opportunities in America, despite the obstacles they faced upon arrival.

Answer:

(if you would like a short one/ still need help)

Nativists we’re prejudice and discriminatory towards Irish emigrants who had come to the United States after the events of the Irish Potato Famine

hope this helps :)

Answer:

905

Step-by-step explanation:

365+540=905

Answer:

905

Step-by-step explanation:

Add the numbers...

365 + 540

Therefore your answer would be 905

Easier and faster if you put it in a calculator but hope this helps!

The general solution to the given differential equation is \(y = cx^2 - 2x^3,\) where c is a constant.

To find the general solution, we first rearrange the given differential equation in the standard form of a linear first-order equation. The equation is:

x^2y' - 2xy = 4

We can rewrite this equation as:

\(y' - (2/x)y = 4/x^2\)

This is now in the form of a linear first-order equation, where the coefficient of y' is 1. To solve this type of equation, we use an integrating factor, which is given by the exponential of the integral of the coefficient of y. In this case, the integrating factor is:

IF = e^(-∫2/x dx) = e^(-2ln|x|) = e^(ln|x|^(-2)) = 1/x^2

Multiplying the entire equation by the integrating factor, we get:

\((1/x^2)y' - 2/x^3 y = 4/x^4\)

Now, the left-hand side of the equation can be written as the derivative of the product of the integrating factor and y:

\(d/dx [(1/x^2)y] = 4/x^4\)

Integrating both sides with respect to x, we have:

\(∫d/dx [(1/x^2)y] dx = ∫4/x^4 dx\)

\(∫(1/x^2)y dx = -4/x^3 + C\)

Integrating the left-hand side gives:

\(-(1/x)y + C = -4/x^3 + C\)

Simplifying further, we get:

\(y = cx^2 - 2x^3\)

where c is the constant obtained by combining the arbitrary constant C with the constant of integration.

Learn more about general solution

brainly.com/question/32554050

#SPJ11

Answer:

the answer is 24

Step-by-step explanation:

add than subtract to get the answer

The correct option regarding the linear regression equation is:

No, the equation is not a good fit because the sum of the residuals is a large number.

To find the equation, we need to insert the points (x,y) in the calculator.

In possession of the equation, the residuals are given by the difference of the predicted values(with the equation) and the actual values.

The model represents a good fit if the sum of the residuals is close to 0.

For this problem, the sum of the residuals is given by:

90 - 50  - 100 - 100 + 150 - 50 = -60.

The sum is a large number, hence the model is not a good fit.

More can be learned about linear regression at https://brainly.com/question/22992800

#SPJ1

Answer:

1. 83% 2.17%

Step-by-step explanation:

Answer:

sorry no a need the point

Answer:

Step-by-step explanation:

to make line perpendicular, the slope should be: slope 1 x slope 2 = -1

first, find slope 1 of y = (-1/5)x + 4, which is: m1 = -1/5

m1 x m2 = -1

-1/5 x m2 = -1

m2= 5

you should use formula for 1 point and 1 slope :

y-y1= m(x-x1)

y+10 = 5(x+6)

y+10 = 5x+30

y = 5x+20

Hope it helps.

Regression analysis is a statistical method for making predictions by using data on the correlation between independent or predictor variables and dependent variables.

Regression analysis, a collection of statistical methods used in statistical modeling, is used to compare a dependent variable (also known as the "outcome" or "response" variable, or a "label" in machine learning jargon) and one or more independent variables (also known as "predictors," "covariates," "explanatory variables," or "features").

In linear regression, the most popular kind of regression analysis, the line (or more complex linear combination) that most closely matches the data in terms of a given mathematical criterion is found.

Regression analysis is employed to deduce the causal relationships between the variables in a given situation. It should be noted that regressions by themselves only reveal relationships between a dependent variable and a set of independent variables in a particular dataset.

To learn more about variables visit:

https://brainly.com/question/15293181

#SPJ4

Answer:

x = -5

Step-by-step explanation:

First, divide -3 on both sides.

Then you will get x = -5

Answer:

x = - 5

x = - 12

Step-by-step explanation:

x² + 17x + 72 = 12

x² + 17x + 72 - 12 = 0

x² + 17x + 60 = 0

(x + 5)(x + 12) = 0

Two separate equations

x + 5 = 0

x + 12 = 0

x + 5 = 0

x + 5 - 5 = 0 - 5

x = - 5

x + 12 = 0

x + 12 - 12 = 0 - 12

x = - 12

The equation of the line in function notation is  

\(y = mx - 3m - 2\)  

Step 1: y - (-2)

To write the equation of the line in function notation, we can use the point-slope form of the equation of a line:

y - y1 = m(x - x1)

where m is the slope of the line, and (x1, y1) is a point on the line. In this case, the slope is given as "m," and the point (x1, y1) is (3, -2).

Substituting these values into the equation, we get:

y - (-2) = m(x - 3)

Simplifying the expression in the left-hand side, we get:

y + 2 = m(x - 3)

This is the equation of the line in point-slope form. To write it in function notation, we can solve for y:

y = mx - 3m - 2

This is the equation of the line in function notation. We can use this equation to find the y-value of the line for any given x-value. For example, if we want to find the y-value of the line when x = 5, we can substitute x = 5 into the equation and solve for y:

y = m(5) - 3m - 2 = 2m - 2

So when x = 5, the y-value of the line is 2m - 2.

Question: Andy wrote the equation of a line that has a slope of "m" and passes through the point (3, -2) in function notation. Write the equation of the line in function notation, showing the first step of your work.

Learn more about "equation of a line" :

https://brainly.com/question/25969846

#SPJ11

Answer:

The inequality for the perimeter to be atleast 300 feet is

Step-by-step explanation:

\(x\geq 142\)

The volume of the helium-filled balloon at 0.855 atm and 10.0 °C will be approximately 42.81 L, calculated using the ideal gas law equation.

To compute this problem, we can use the ideal gas law, which states that PV = nRT, where P is the pressure, V is the volume, n is the number of moles, R is the gas constant, and T is the temperature in Kelvin.

First, we need to convert the initial temperature of 25 °C to Kelvin:

T1 = 25 + 273.15 = 298.15 K

Next, we can rearrange the ideal gas law equation to solve for V2:

V2 = (P1 * V1 * T2) / (P2 * T1)

We have:

P1 = 1.08 atm (initial pressure)

V1 = 50.0 L (initial volume)

P2 = 0.855 atm (final pressure)

T2 = 10.0 °C (final temperature)

Converting the final temperature to Kelvin:

T2 = 10 + 273.15 = 283.15 K

Substituting the values into the equation:

V2 = (1.08 * 50.0 * 283.15) / (0.855 * 298.15)

V2 ≈ 42.81 L

Therefore, the volume of the helium-filled balloon at 0.855 atm and 10.0 °C will be approximately 42.81 L.

To know more about ideal gas law refer here:

https://brainly.com/question/30458409#

#SPJ11

The center of mass of the metal plate with density rho(x,y) = αx+ βy g/cm2 must lie on the line x + y = 7/6.

To find the center of mass of the metal plate, we need to calculate the coordinates of its centroid (X, Y). The coordinates of the centroid are given by:

X = (1/M) ∬(R) x ρ(x,y) dA, Y = (1/M) ∬(R) y ρ(x,y) dA

where M is the total mass of the plate, R is the region of integration (0 ≤ x ≤ 1, 0 ≤ y ≤ 1), and dA is the differential area element.

We can calculate the total mass M of the plate as follows:

M = ∬(R) ρ(x,y) dA = α/2 + β/2 = (α + β)/2

Using the given density function, we can calculate the integrals for X and Y:

X = (1/M) ∬(R) x ρ(x,y) dA = (2/αβ) ∬(R) x(αx+βy) dA = (2/3)(α+β)

Y = (1/M) ∬(R) y ρ(x,y) dA = (2/αβ) ∬(R) y(αx+βy) dA = (2/3)(α+β)

Thus, the coordinates of the centroid are (X, Y) = ((2/3)(α+β), (2/3)(α+β)).

Now, if we substitute X + Y = (4/3)(α+β) into the equation x + y = 7/6, we get:

x + y = 7/6

2x + 2y = 7/3

2(x+y) = 4/3(α+β)

x+y = (2/3)(α+β)

which shows that the centroid lies on the line x + y = 7/6. Therefore, the center of mass must also lie on this line.

For more questions like Integral click the link below:

https://brainly.com/question/22008756

#SPJ11

Therefore , the solution of the given problem of equation comes out to be  y = 23.78t - 5t²

An equation is a mathematical formula that connects two assertions using the equal sign (=) to denote equivalence. In algebra, an equation is a mathematical statement that establishes the equivalence of two mathematical expressions. For instance, an equal sign separates the components 3x + 5 and 14 in the equation 3x + 5 = 14. A mathematical formula is used to explain the connection between two sentences on either side of a letter. Frequently, there is just one variable, which is also the symbol. for example, 2x - 4 = 2.

Here,
Given :parametric equation

x be the speed of water

t be the time

v be the speed of dolphin

=> x = (vcosx)t +x₀

=> v = 32

=> x = 48

=> x = (32 X cos 48)t + 0

=> x = 21.41t

thus,

=>  y = (vsintx)t - 1/2gt² + y₀

=>   y₀ = 0

=>  v = 32

=> x = 48

=> g = 10

=> y = (32sin48)t -1/2 *10*t² +0

=>  y = 23.78t - 5t²

To know more about equation visit:

brainly.com/question/649785

#SPJ4

In summary, regardless of the values of μ and σ, you can calculate z-scores by subtracting the mean from the value of interest and then dividing by the standard deviation.

To find z-scores for normal distributions where μ (mean) is not equal to 0 or σ (standard deviation) is not equal to 1, you need to use the formula for standardizing a value using the z-score formula:

z = (x - μ) / σ

Here, x is the value you want to standardize, μ is the mean of the distribution, and σ is the standard deviation.

To find the z-score for a specific value, you subtract the mean from that value and then divide the result by the standard deviation. This calculation allows you to determine how many standard deviations away from the mean the value is.

For example, if you have a normal distribution with a mean of 10 and a standard deviation of 2, and you want to find the z-score for a value of 14, you would use the formula:

z = (14 - 10) / 2

z = 4 / 2

z = 2

The z-score of 2 indicates that the value of 14 is two standard deviations above the mean.

To know more about standard deviation,

https://brainly.com/question/16896775

#SPJ11

Answer:

(2*100,000)+(7*10,000)+(9*100)+(5*10)

Vector is the quantity that has magnitude as well as direction. The component form of the vector that translates P(-3,6) to P'(-4,8)  is -i + 2j.

A vector quantity has both magnitude and direction. It is added using parallelogram law of addition.

The sum of two vector quantities is always a vector quantity.

The sum of two vector quantities can vary from their scalar difference to their scalar addition.

The given points are P(-3,6) to P'(-4,8) .

The vector component form of two points (x₁,y₁) and (x₂,y₂) is given by ,

(x₂-x₁)i + (y₂-y₁)j

Therefore, The vector component form of given points are,

(-4-(-3))i + (8-6)j

-i + 2j.
Hence "The component form of the vector that translates P(-3,6) to P'(-4,8) -i + 2j.

To learn more about vectors click on the following link

https://brainly.com/question/13322477

#SPJ1

The 40% clearance discount is already factored into the clearance price of $30, so applying the 20% coupon only reduces the price further by 20% of $30, or $6. Therefore, you would pay $24 for the item with both discounts applied.

Let's break down the discounts and calculate the final price of the item using the terms "normal", "price", and "quantitatively".
The normal price of the item: $50

First, apply the 40% clearance discount:
40% off the normal price = 0.4 * $50 = $20

Subtract the clearance discount from the normal price:
New discounted price = $50 - $20 = $30

Now, apply the 20% off coupon to the discounted price:
20% off the new discounted price = 0.2 * $30 = $6

Quantitatively, the calculation would be:
Normal price = $50
Clearance price (40% off) = $30
Coupon discount (20% off clearance price) = 0.20 x $30 = $6
Final price = $30 - $6 = $24

Subtract the coupon discount from the discounted price:
Final price = $30 - $6 = $24

So, you should pay $24 for the item. It is not the same as taking 60% off the normal price because the discounts are applied sequentially, not combined. Quantitatively, you can see that taking 60% off the normal price would result in a $30 discount ($50 * 0.6), while the actual total discount here is $26 ($20 + $6).

Learn more about Discount:

brainly.com/question/3541148

#SPJ11

Answer:

Both are 1/2

Step-by-step explanation:

Count just the tails, that's the numerator

Count all the heads and tails, that's the denominator.

And for the 2nd fraction:

Count just the evens, that's the numerator

Count all the even and odd numbers, that's the denominator.

Answer: The answer to this question is 3/4

Step-by-step explanation:

In this problem, there are 12 outcomes. Of those, 3 result in an even number and a tail, 3 more in an even number but not tail and 3 in a tail but an odd number, hence there are 9 desired outcomes.

Hence, the probability is given by: p=9/12=3/4

The corollary states that for every positive real number ε, there exists a positive integer n such that

The corollary of the Archimedean principle states that for any positive real number ε, there exists a positive integer n such that ε is greater than the reciprocal of n, i.e., ε > 1/n. In other words, there exists a positive integer n such that the fraction 1/n is smaller than any given positive real number ε.

To prove this corollary, we can assume that ε is a positive real number. By the Archimedean principle, there exists a positive integer m such that m > ε. Now, consider the positive integer n = ⌈1/ε⌉ + 1, where ⌈x⌉ denotes the ceiling function, rounding up x to the nearest integer.

We have:

1/ε < 1/(⌈1/ε⌉ + 1) ≤ 1/(1/ε) = ε.

Therefore, we can conclude that for any positive real number ε, there exists a positive integer n = ⌈1/ε⌉ + 1 such that ε > 1/n.

Learn more about corollary states

brainly.com/question/13485668

#SPJ11