Answers
Answer:
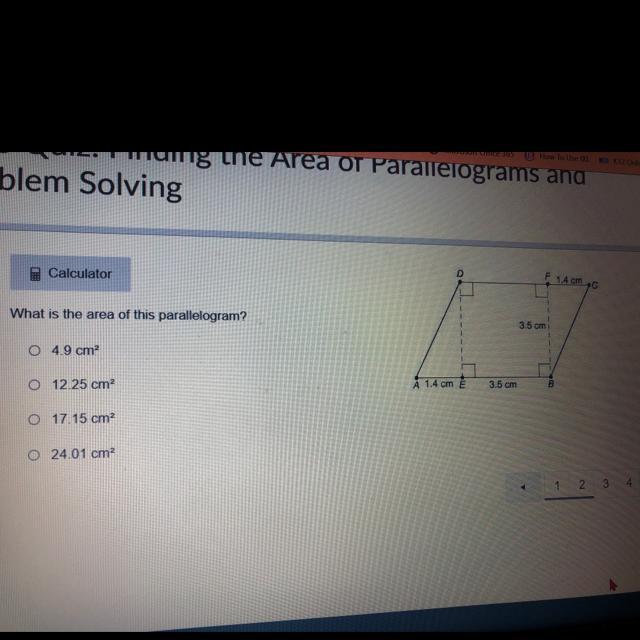
B. 12.25
Step-by-step explanation:
A=bxh=3.5·3.5=12.25
Answer:
17.15
Step-by-step explanation:
There are 2 ways to solve this.
One way is this:
Add 1.4 and 3.5 together to get the total length of the parallelogram. The sum would be 4.9. Then multiply this number by the height of the figure(3.5cm). So that the product of 4.9 and 3.5 is 17.15.
The second way is this:
Find the area of the two triangles and the square and then add those products together. So add:
1.4 x 3.5 ÷21.4 x 3.5 ÷23.5 x 3.5So solve this equation and you will get:
2.45 + 2.45 + 12.25=17.15Related Questions
For each pair of functions f and g below, find f(g(x)) and g (f(x)).
Then, determine whether fand g are inverses of each other.
Simplify your answers as much as possible.
(Assume that your expressions are defined for all x in the domain of the composition.
You do not have to indicate the domain.)
f(x) = x+4
g (x) = x+4
Answers
The Function f(g(x)) = g(f(x)) = x + 8.
The functions are: f(x) = x + 4 and g(x) = x + 4. We can find f(g(x)) by substituting g(x) in place of x in f(x).
f(g(x)) = f(x + 4) = (x + 4) + 4 = x + 8
Similarly, we can find g(f(x)) by substituting f(x) in place of x in g(x).g(f(x)) = g(x + 4) = (x + 4) + 4 = x + 8
Thus, we can see that f(g(x)) and g(f(x)) are equal to each other,
which is x + 8.
To learn more about : Function
https://brainly.com/question/11624077
#SPJ8
A student solves the following problem:
Problem: 2(x−3)+3x=19
Step 1: 2x−6+3x=19
Step 2: 6x−6=19
Step 3: 6x−6 + 6=19 + 6
Step 4: 6x=25
Step 5: 6x6=256
Step 6: x≈4.17
Where is the mistake? What did the student do incorrectly?
Responses
Step 3: Student should have subtracted 6 from both sides, not added 6.
Step 5: Student should have subtracted 6 from both sides, not divided by 6
Step 1: Student should have only distributed the 2 to the x and not the x & 3.
Step 2: Student should have added 2x + 3x = 5x, not 2 x 3 = 6x
Answers
Answer:
error in Step 2
Step-by-step explanation:
2(x - 3) + 3x = 19
Step 1 : 2x - 6 + 3x = 19 ← simplify left side by collecting like terms
Step 2 : 5x - 6 = 19 ← add 6 to both sides
Step 3 : 5x - 6 + 6 = 19 + 6
Step 4 : 5x = 25 ← divide both sides by 5
Step 5 : x = 5
Error was made by student in Step 2 who should have added 2x and 3x, not multiplied 2 × 3
Find the percent change to the nearest whole percent. from 45 feet to 95 feet.
Answers
Answer:
211%
Step-by-step explanation:
To calculate the percentage change between these two numbers we need to divide the end result from the initial starting point. Once we do this we need to multiply the product by 100 to get the percentage value.
95 / 45 = 2.11111
2.11111 * 100 = 211.11%
Finally, we can see that the percentage change from 45 ft. to 95 ft. is 211.11%. If we round this to the nearest whole percent it would be a change of 211%
Is landing on a number less then 10 on a 6 sided dice impossible?
Answers
Answer:yes
Step-by-step explanation:
if you have two dice one dice can land on a 4 and 6
(1 point) 1. The height (in feet) and volume of usable lumber (in cubic feet) of 32 cherry trees are measured by a researcher. The goal is to determine if volume of usable lumber can be estimated from the height of a tree. The results are plotted below.(a) In this study, the response variable isA. neither height nor volume. The measuring instrument used to measure height is the response variable.B. height or volume. It doesn't matter which is considered the response.C. volume.D. height.
Answers
Answer:
C. volume
Step-by-step explanation:
The response variable in this scenario would be the volume of the usable lumber. That is because this variable depends completely on the height of the cherry trees that are being measured. The higher that the cherry trees are the more volume can be expected to get from cutting these trees down. The opposite goes for trees that are smaller, they would decrease the total expected volume that will be received from the usable lumber since there would be less amount of tree to cut down.
solve the PDE using separation of variables method Uxx = 1/2 Ut 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Answers
The general solution of the partial differential equation is:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
How to solve Partial Differential Equations?The partial differential equation (PDE) is given as:
Uxx = (1/2)Ut with the boundary and initial conditions as 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Assume that the solution can be written as a product of two functions:
U(x, t) = X(x)T(t)
Substituting this into the PDE, we have:
X''(x)T(t) = (1/2)X(x)T'(t)
Dividing both sides by X(x)T(t), we get:
(X''(x))/X(x) = (1/2)(T'(t))/T(t)
Since the left side only depends on x and the right side only depends on t, both sides must be equal to a constant, denoted as -λ²:
(X''(x))/X(x) = -λ²
(1/2)(T'(t))/T(t) = -λ²
Simplifying the second equation, we have:
T'(t)/T(t) = -2λ²
Solving the second equation, we find:
T(t) = Ce^(-2λ²t)
Applying the boundary condition U(0, t) = 0, we have:
U(0, t) = X(0)T(t) = 0
Since T(t) ≠ 0, we must have X(0) = 0.
Applying the boundary condition U(3, t) = 0, we have:
U(3, t) = X(3)T(t) = 0
Again, since T(t) ≠ 0, we must have X(3) = 0.
Therefore, we can conclude that X(x) must satisfy the following boundary value problem:
X''(x)/X(x) = -λ²
X(0) = 0
X(3) = 0
The general solution to this ordinary differential equation is given by:
X(x) = Asin(λx) + Bcos(λx)
Applying the initial condition U(x, 0) = 5*sin(4πx), we have:
U(x, 0) = X(x)T(0) = X(x)C
Comparing this with the given initial condition, we can conclude that T(0) = C = 5.
Therefore, the complete solution for U(x, t) is given by:
U(x, t) = Σ [Aₙsin(λₙx) + Bₙcos(λₙx)]*e^(-2(λₙ)²t)
where:
Σ represents the summation over all values of n
λₙ are the eigenvalues obtained from solving the boundary value problem for X(x).
To find the eigenvalues λₙ, we substitute the boundary conditions into the general solution for X(x):
X(0) = 0: Aₙsin(0) + Bₙcos(0) = 0
X(3) = 0: Aₙsin(3λₙ) + Bₙcos(3λₙ) = 0
From the first equation, we have Bₙ = 0.
From the second equation, we have Aₙ*sin(3λₙ) = 0. Since Aₙ ≠ 0, we must have sin(3λₙ) = 0.
This implies that 3λₙ = nπ, where n is an integer.
Therefore, λₙ = (nπ)/3.
Substituting the eigenvalues into the general solution, we have:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
where Aₙ are the coefficients that can be determined from the initial condition.
Read more about Partial Differential Equations at: https://brainly.com/question/28099315
#SPJ1
28+16x^4 i need it factored completely
Answers
Answer:
\(4(x^4+7)\)
Step-by-step explanation:
Taking out the greatest common factor,\(16x^4+28=4(x^4+7)\).
10. Kipp constructed a pentagonal pyramid for his social studies report. The base had an area of 12 cm². It took 48 cubic centimeters of clay to make his model. Find the height of the pyramid.
Answers
We can use the formula for the volume of a pentagonal pyramid to solve this problem:
Volume = (1/3) × Base Area × Height
We know that the base area is 12 cm² and the volume is 48 cubic centimeters. We can substitute these values into the formula and solve for the height:
48 = (1/3) × 12 × Height
Multiplying both sides by 3 gives:
144 = 12 × Height
Dividing both sides by 12 gives:
Height = 12
Therefore, the height of the pentagonal pyramid is 12 centimeters.
Here is a list of questions about the students and teachers at a school. Select the questions that are statistical questions.
Answers
As observed, all the questions in the list can be answered on the basis of some data collection and analysis.
So they all can be considered as statistical questions.
Thus, all the questions in the given list are statistical questions.
1.
If you have to answer the question for most popular lunch choice, you have to collect data of the lunch choices by a large portion of the called population. Then the lunch choice corresponding to highest frequency will be considered as the most popular lunch choice. Since the conclusion is data driven, this is a statistical question.
2.
In order to answer the question, you need to collect the information about the name of school each of the called population is admitted to. If all the students are found to be admitted to the same school, then the name of that school would be the answer.
Here also, the conclusion is data driven, so this is also a statistical question.
3.
To answer this question, you have to gather all the teaching staff of the school, and take individual answers to which subject they teach. The number of teachers who answered math will be the answer for this question.
Here also, the conclusion is data driven, so this is also a statistical question.
4.
To answer this question, you have to gather the individual age of each teacher in the school. The age corresponding to the maximum frequency would be the answer to this question.
Here also, the conclusion is data driven, so this is also a statistical question.
5.
To answer this question, you have to collect data about how much sleep each student gets in the school. Then only you can answer this question.
Since the conclusion is data driven, this is a statistical question.
6.
To answer this question, you have to collect data that how many students travel by which mode of transport to travel from home to school. The mode corresponding to highest frequency is the answer to this question.
Here also, the conclusion is data driven, so this is also a statistical question.
Thus, it is seen that all the six questions are statistical questions.
Find one value of x for which h(x)=4 and find h (-2)
Answers
the solutions are:
h(x) = 4 for x = 0h(-2) = 2How to find the value of x for which h(x) = 4?The only information of h(x) that we have is the given graph.
To find the value of x, we need to go to the vertical axis and find y = 4, then we move horizontally to the left until we meet the curve.
That intersection will give the value of x for which h(x) = 4.
Doing that, we conclude that h(x) = 4 when x = 0 (on the vertical axis).
Now we want to find h(-2), and we can do that using the graph.
By finding x = -2 on the horizontal axis and then moving up until we intercept the graph, we can see that:
h(-2) = 2
Concluding, the solutions are:
h(x) = 4 for x = 0h(-2) = 2If you want to learn more about parabolas:
https://brainly.com/question/4061870
#SPJ1
A model rollercoaster is built to a scale of 1:32. In the model rollercoaster, the angle between the ground and the steepest slope is 110°. What is the angle between the ground and steepest slope on the real rollercoaster?
Answers
The angle between the ground and the steepest slope on the real rollercoaster is approximately 89.998°.
A model rollercoaster is built to a scale of 1:32. In the model rollercoaster, the angle between the ground and the steepest slope is 110°.What is the angle between the ground and the steepest slope on the real rollercoaster?
To determine the angle between the ground and the steepest slope on the real rollercoaster, you need to consider the scale of the model rollercoaster.To find the real rollercoaster angle, you should use a scale factor that relates the model rollercoaster to the real one.
The scale factor should multiply the model angle to obtain the real one. Since the scale factor relates the model length to the real length, it should relate the horizontal distance and the vertical height.
The horizontal and vertical lengths are in a ratio of 32:1 for the model. This means that for every 32 units in the model, there is one unit in the real rollercoaster. Therefore, we can say that the horizontal length of the real rollercoaster is 32 times the horizontal length of the model rollercoaster.
That is:h(real) = 32h(model)Similarly, the vertical height of the real rollercoaster is 32 times the vertical height of the model rollercoaster. That is:v(real) = 32v(model)
The tangent of an angle equals the vertical height divided by the horizontal distance. Therefore, the tangent of the real angle equals the tangent of the model angle times the scale factor.
That is:tanθ(real) = 32tanθ(model)By substitution,θ(real) = arctan(32tanθ(model))For the given model angle of 110°,
the corresponding real angle is:θ(real) = arctan(32tan110°)θ(real) = arctan(32(-2.74747741945462))θ(real) = arctan(-87.91927694142864)θ(real) ≈ -89.998°
The negative sign indicates that the angle is measured below the horizontal line.
To learn more about : angle
https://brainly.com/question/25770607
#SPJ8
a) Suppose you are a designer making the traffic sign above. What is the sum of the interior angles of the equilateral triangle? What is the measure of ∠N? What is the measure of ∠M? Explain your reasoning. (2 points)
b) What is the sum of the exterior angles of the equilateral triangle ∠M + ∠R + ∠X? Explain your reasoning. (2 points)
Answers
a). Sum of the angles of a equilateral triangle = 180°
As, All sides are equal, All angles also will be equal.
3s = 180°
s = 180/3
s = 60°
Since, ∠N = 60°
∠M + ∠N = 180° (Strait Angles = 180°)
∠M + 60° = 180°
∠M = 180° - 60°
∠M = 120°
Therefore, ∠M = 120° , ∠N = 60°
b). ∠M + ∠N = 180° (Strait Angles = 180°)
∠M + 60° = 180°
∠M = 180° - 60°
∠M = 120°
∠R + ∠Q = 180° (Strait Angles = 180°)
∠R + 60° = 180°
∠R = 180° - 60°
∠R = 120°
∠X + ∠V = 180° (Strait Angles = 180°)
∠X + 60° = 180°
∠X = 180° - 60°
∠X = 120°
Therefore, ∠M + ∠R + ∠X = 120 + 120 + 120 = 360°
12. Which of the following represents the linear equation 3(x + 2) = 12 - 2y in standard \ A|y=-3/2x+3 [B] y = 3/2x-3 3x - 2y = 10 D 3x + 2y = 6
Answers
Answer: The answer is D. 3x+2y=6, please mark me as brainliest, I want my brainliest back and I want very helpful for good!!!
Step-by-step explanation:
A new tire had a tread depth of
5
8 in. After driving one year the tire had
17
32 in. of tread remaining. What percent of the tread was worn?
Answers
Answer:
15%
Step-by-step explanation:
Thomas is playing with his trainset on the patio. He aligns6 tracks in a single line. Ifeach track measures 6.8inches, what is the totallength of the track?(Tutors please explain how you do the equation ex:division, please explain how you divide each number etc)
Answers
Given that:
- Thomas aligns 6 tracks in a single line.
- The length of each track is 6.8 inches.
Let be "x" the total length of the track (in inches).
Based on the data given in the exercise, you can set up that:
\(x=(6.8)(6)\)Therefore, in order to find the total length, you need to multiply the length of each track by the number of tracks aligned. You can solve the multiplication as follows:
1. Set up that:
2. Multiply the 8 by 6. You know that:
\(8\cdot6=48\)But you only need to write the second digit (8) below the line.
3. Multiply the 6 by 6 and add the digit 4 (of the value 48 obtained in the previous step) to the result. Write the number obtain below the line.
Then:
4. You can identify that there is a Decimal Number in the Multiplication (this is 6.8), and you can also identify that it has only one digit after the Decimal Point.
This indicates that you need to put only one digit behind the Decimal Point of the Product (the result of the Multiplication).
Then:
Hence, the answer is:
\(40.8\text{ }inches\)
Solve (list all answers as whole numbers, reduced roots or fractions, NO DECIMALS 1. 5(x - 7) = 9 - 2x + 5 2 MATH TO Module 2 Homework
Answers
5(x -7) = 9 - 2x + 5
5x - 35 = 9 - 2x + 5 (Distributing)
5x + 2x - 35 = 9 + 5 (Adding 2x to both sides of the equation)
5x + 2x = 35 + 9 + 5 (Adding 35 to both sides of the equation)
7x = 49 (Adding like terms)
x = 49/7 (Dividing by 7 on both sides of the equation)
x= 7 (Dividing)
The answer is x=7.
In Ellen's math class, there are 2 boys for every 3 girls. If there are 21 girls in the class, how many boys are in the class?
Answers
Answer: 14 boys
Step-by-step explanation:
ratio 2:3
7 divided by 21 = 3, so 7 times 2 equals 14
Answer:
14
Step-by-step explanation:
Divide 21 by 3, you get 7. Multiply 7 by 2, you get 14.
The conditional statement below is true. If possible, write the biconditional statement.
If 2x = 18, then x = 9.
Answers
The biconditional statement for the given conditional statement would be:
2x = 18 if and only if x = 9.
The given conditional statement "If 2x = 18, then x = 9" can be represented symbolically as p → q, where p represents the statement "2x = 18" and q represents the statement "x = 9".
To form the biconditional statement, we need to determine if the converse of the conditional statement is also true. The converse of the original statement is "If x = 9, then 2x = 18". Let's evaluate the converse statement.
If x = 9, then substituting this value into the equation 2x = 18 gives us 2(9) = 18, which is indeed true. Therefore, the converse of the original statement is true.
Based on this, we can write the biconditional statement:
2x = 18 if and only if x = 9.
The biconditional statement implies that if 2x is equal to 18, then x must be equal to 9, and conversely, if x is equal to 9, then 2x is equal to 18. The biconditional statement asserts the equivalence between the two statements, indicating that they always hold true together.
In summary, the biconditional statement is a concise way of expressing that 2x = 18 if and only if x = 9, capturing the mutual implication between the two statements.
for such more question on conditional statement
https://brainly.com/question/27839142
#SPJ8
Charlotte had to distribute 71 dollars among 6 people. What is left with Charlotte after distribution if all six got maximum equal dollars?
Answers
Answer:
5?
Step-by-step explanation:
A salesperson at a jewelry store earns 5% commission each week. Last week, Heidi sold 640 worth of jewelry. How much did Heidi make in commission? How much did the jewelry store make from sales?
Answers
Answer:
12,800 Dollars USD
Step-by-step explanation:
PLEASE HELP ILL GIVE BRAINLIESTTTT
Answers
Answer:
(1.5,-0.5)
Step-by-step explanation:
We can see that is true because the distance from K to H is the same as that from H to M
equality of fractions
Answers
Answer:
Fractions are equal when one fraction can be obtained from the other.
Step-by-step explanation:
equality means a relationship between two quantities or, more generally two mathematical expressions, asserting that the quantities have the same value, or that the expressions represent the same mathematical object.
-) A freight train left Berlin and traveled
toward Johannesburg at an average speed
of 45 km/h. Sometime later a passenger
train left traveling in the same direction
but at an average speed of 72 km/h. After
traveling for ten hours the passenger train
caught up with the freight train. Find the
number of hours the freight train traveled
before the passenger train caught up.
4
Answers
Therefore, the freight train traveled for 16.67 + 10 = 26.67 hours before the passenger train caught up with it.
let's call the time it took for the passenger train to catch up with the freight train "t" (in hours).
During this time, the freight train traveled at its average speed of 45 km/h for t + 10 hours, while the passenger train traveled at its average speed of 72 km/h for t hours.
We know that the distance both trains traveled is the same, since the passenger train caught up with the freight train. So, we can set up the following equation:
distance traveled by freight train = distance traveled by passenger train
\((45 km/h) x (t + 10 h) = (72 km/h) x t\)
Simplifying this equation, we get:
\(45t + 450 = 72t\)
\(27t = 450\)
t = 16.67 hours
Therefore, the freight train traveled for 16.67 + 10 = 26.67 hours before the passenger train caught up with it.
To know more about hours, visit:
https://brainly.com/question/13533620
#SPJ1
Solve the equation and check your solution. 5 t = 7 and one-half Multiply 5t by 5; the answer is 7 and one-half. Divide 5t by 5; the answer is 7 and one-half. Divide both sides by 5; the answer is 1 and one-half. Multiply both sides by 5; the answer is 37 and one-half.
Answers
Answer: the answer is 13 and one-half
Step-by-step explanation:
C
Step-by-step explanation:
6. With the origin at Champaign, the coordinates for Springfield and Bloomington on the map shown are (-74, -21) and
(-29, 27), respectively. Assuming the coordinates are given in miles, find the distance between the two cities. Round to
the nearest tenth of a mile. Show your work!
55
80
70
74
65
65
7. A recent news article reported that according to a poll, only 29% of Americans support a proposed infrastructure plan.
At the bottom of the article was the following sentence: "The Post-ABC poll was conducted by telephone Jan. 12-15,
2017, including landline and cellphone respondents. Overall results have a margin of sampling error of plus or minus
3.5 percentage points." The confidence level was not given. Supposing the confidence level was 95%, write a sentence
or two explaining the results of the poll.
For Questions 8 and 9: In conducting a survey of 200 students, a researcher found that 22% had significant (more than $1,000)
credit card debt.
8. Calculate the margin of error with a 95% confidence level for this survey.
9. If the researcher wanted to get a margin of error of 4%, how many total students would she need to survey? Assume the
number of students with significant credit card debt stays at 22%.
Answers
Answer:
6. To find the distance between Springfield and Bloomington, we can use the distance formula:
d = sqrt((x2 - x1)^2 + (y2 - y1)^2)
where (x1, y1) = (-74, -21) and (x2, y2) = (-29, 27). Substituting these values into the formula, we get:
d = sqrt((-29 - (-74))^2 + (27 - (-21))^2) = sqrt(45^2 + 48^2) = sqrt(4059) ≈ 63.7
Therefore, the distance between Springfield and Bloomington is approximately 63.7 miles.
7. With a confidence level of 95% and a margin of error of plus or minus 3.5 percentage points, we can interpret the results of the poll as follows: if the same poll were conducted many times, 95% of the time the percentage of Americans who support the proposed infrastructure plan would fall within 3.5 percentage points of the reported value of 29%. In other words, the true percentage of Americans who support the plan is likely to be between 25.5% and 32.5%, with a high degree of confidence.
8. To calculate the margin of error with a 95% confidence level, we can use the formula:
margin of error = zsqrt(p(1-p)/n)
where z is the z-score associated with a 95% confidence level (which is approximately 1.96), p is the proportion of students with significant credit card debt (which is 0.22), and n is the sample size (which is 200). Substituting these values into the formula, we get:
margin of error = 1.96sqrt(0.22(1-0.22)/200) ≈ 0.07
Therefore, the margin of error for this survey with a 95% confidence level is approximately 0.07, or 7%.
9. To find the sample size needed to achieve a margin of error of 4%, we can use the formula:
n = (zsqrt(p(1-p))/e)^2
where z is the z-score associated with a 95% confidence level (which is approximately 1.96), p is the proportion of students with significant credit card debt (which is 0.22), and e is the desired margin of error (which is 0.04). Substituting these values into the formula, we get:
n = (1.96sqrt(0.22(1-0.22))/0.04)^2 ≈ 1385
Therefore, the researcher would need to survey approximately 1385 students to achieve a margin of error of 4%.
Step-by-step explanation:
Given f (x) = 1/2 * x - 5 find f ^ -1 * (x)
Answers
Answer: d i think im pretty sure
Step-by-step explanation:
davey read 58 pages on saturday and p pages on
Answers
The value of p is 15
What is the unitary method?The unitary method is a method in which you find the value of a unit and then the value of a required number of units.
Given here: Davey reads 58 pages on Saturday and on rest of the days p pages per day
Therefore everyday he reads 58+p pages per day
If he reads for 10 days and he reads a total 1408 pages then we have
In a week there is one Saturday
thus
9p+58=1408
9p=1350
p=15
Thus on the other days p is equal to 15 pages per day.
Learn more about the unitary method here:
https://brainly.com/question/22056199
#SPJ1
The complete question is Davey reads 58 pages on Saturday and p pages on other days and on a span of 10 days he reads 1408 pages. Find the value of p.
74,626,831.08 ROUNDED TO THE TENTH.
Answers
Answer:
74,626,831.1
Step-by-step explanation:
You'd notice that in the 0.8 part that the number 8 is greater than 5, and with rounding, if the number if 5 or over, then you round the decimal place before it to a number higher.
what is the greatest commen factor of 15 and 64
Answers
Let's factor out 15.
15:1 × 15, 3 × 5.
Let's factor out 64.
64:1 × 64, 2 × 32, 4 x 16, 8 × 8.
Both numbers have 1, so the GCF of 15 and 64 is 1.
Thope this helps you, PM me if you need help understanding. :)
Answer: The greatest common factor for 15 and 64 is 1.
If the square of a positive integer is added to four times to integer the result is 117 find the integer.
Answers
Answer:
x = -2 ± 452i
Step-by-step explanation:
x² + 4x = 117
x² + 4x - 117 = 0
if you solve this quadratic by using the quadratic formula you get:
x = -2 ± 452i
452i is an imaginary number that equals \(\sqrt{-452}\)