Answers
Answer:
n^10/(144m^4)
Step-by-step explanation:
The applicable rules of exponents are ...
(a^b)^c = a^(bc)
(a^b)(a^c) = a^(b+c)
(a^b)/(a^c) = a^(b-c)
a^-b = 1/a^b
(ab)^c = (a^c)(b^c)
__
Using these rules, we can simplify the given expression as follows:
\(\left(\dfrac{3m^{-5}n^2}{4m^{-2}n^0}\right)^2\left(\dfrac{mn^4}{9n}\right)^2=\left(\dfrac{3}{4}m^{-5(-(-2))}n^{2-0}\right)^2\left(\dfrac{1}{9}mn^{4-1}\right)^2\\\\=\left(\dfrac{3n^2}{4m^3}\right)^2\left(\dfrac{m^3}{9}\right)^2=\dfrac{3^2n^4}{4^2m^6}\cdot\dfrac{m^2n^6}{9^2}=\boxed{\dfrac{n^{10}}{144m^4}}\)
Related Questions
5 – 4|1 + 2x| = -3
Solve for x in simplest form
Answers
Answer:
\(x = \frac{1}{2} \)
\(x = - \frac{3}{2} \)
Find x. Sum of angle measures: 360

Answers
Answer:
126
Step-by-step explanation:
→ Find the sum of the angle
x + x - 35 + x - 46 + 0.5x = 3.5x - 81
→ Equate to 360
3.5x - 81 = 360
→ Add 81 to both sides
3.5x = 441
→ Divide both sides by 3.5
x = 126
consider this equation y=-1/2x+4 1/2 and 3x - 4y = 12 solve the system by graphing. label each graph
Answers
On solving the equations y = (-1/2)x + \(4\frac{1}{2}\) and 3x - 4y = 12 graphically , the solution is (6 , 3/2) .
In the question ,
it is given that
the equations are y = (-1/2)x + \(4\frac{1}{2}\) and 3x - 4y = 12
which can be written as y = (-1/2)x + 9/2 and 3x - 4y = 12
to plot the graph of the given equations , we need intercept .
For the equation y = (-1/2)x + 9/2
when x= 0 , y = (-1/2)(0) + 9/2 = 9/2
when y = 0 ,
0 = (-1/2)x + 9/2
(1/2)x = 9/2
x = 9
the points are (0 , 9/2) and (9 , 0)
For the equation 3x - 4y = 12
when x = 0 , 3(0) - 4y = 12
-4y = 12
y = -3
when y = 0 , 3x -4(0) = 12
3x = 12
x = 4
the points are (0,-3) and (4,0) .
after plotting the lines on the graph , we can see that the both the lines intersect at the point (6 , 3/2) ,
Therefore , On solving the equations y = (-1/2)x + \(4\frac{1}{2}\) and 3x - 4y = 12 graphically , the solution is (6 , 3/2) .
The given question is incomplete , the complete question is
Consider this equation y = (-1/2)x + \(4\frac{1}{2}\) and 3x - 4y = 12 .
Solve the system by graphing. label each graph.
Learn more about Equations here
https://brainly.com/question/16922919
#SPJ1

which of these is most likely to weigh 2 kilograms car roast chicken horse egg tea bag
Answers
The item most likely to weigh 2 kilograms is a roast chicken.
Which of them would weight 2 kilograms?
The size, breed, and any other ingredients or stuffing used can all affect the weight of a roast chicken. Weights of roast chickens can range from petite ones weighing less than 1 kilogram to larger ones weighing more than 2 kilograms.
The other things that we have there would either weigh less than 2 Kg such as a tea bag or much more than 2 Kg such as a horse. The egg and the tea a very light and would be less than 2 Kg in weight while the bag and the horse would be above 2 Kg in weight.
Learn more about weight:https://brainly.com/question/31659519
#SPJ1
What is the domain of the given function?
{(3, –2), (6, 1), (–1, 4), (5, 9), (–4, 0)}
Answers
the answer is
{x|x= -4,-1,3,5,6}
The table represents a linear function. What is the slope of the function?
A. -3 B. -2 C. 3 D.4
Answers
Answer:
B
Step-by-step explanation:
If A = {3, 5, 7, 8, 9, 10} and B= {1,4,7,9,11,12}
Find
a) ANB=
b) AUB=
Answers
Answer:
pls mark as brainliest
Step-by-step explanation:
If A = {3, 5, 7, 8, 9, 10} and B= {1,4,7,9,11,12}
a) ANB= { 7 , 9 }
b.)AUB= { 1 , 3 , 4 , 5 , 7 , 8 , 9 , 10 , 11 , 12 }
In order to determine the average price of hotel rooms in Atlanta, a sample of 64 hotels was selected. It was determined that the average price of the rooms in the sample was $108.50 with a standard deviation of $16.
a) Formulate the null and alternative hypotheses to determine whether or not the average room price is significantly different from $112.
b) Compute the test statistic.
c) Using the p-value approach, what is your conclusion? Let alpha = .05.
d) Using the critival value approach, what is your conclusion? Let alpha = .05.
e) Write a concluding statement based on your answers above.
Answers
Answer:
C
Step-by-step explanation:
y = (x - 5) (x + 2) , when x=3
Answers
Answer:
-10
Step-by-step explanation:
y = (x - 5) (x + 2)
y = (3 - 5) (3 + 2)
y= (-2) (5)
y= -2 x 5
y= -10
Howdy! Thanks for stopping by my question! I would really appreciate the help! I've attached the question below. Thanks!
I'd appreciate if you made sure to double check your answers and provide everything the question is asking! INCLUDE ALL STEPS!

Answers
Answer:
a) x = 1 ± (3/7)√7
b) (-∞, -5) ∪ [-2, 5) ∪ [6, ∞)
Step-by-step explanation:
You want solutions to the relations ...
7 +1/x = 1/(x-2)(x² -4x -12)/(x² -25) ≥ 0a) 7 + ...We like to solve these in the form f(x) = 0. It helps avoid extraneous solutions.
\(7+\dfrac{1}{x} -\dfrac{1}{x-2}=0\\\\\\\dfrac{7x+1}{x}-\dfrac{1}{x-2}=0\\\\\\\dfrac{(7x+1)(x-2)-x}{x(x-2)}=0\\\\\\ \dfrac{7x^2-14x-2}{x(x-2)}=0\)
The roots of the numerator quadratic are found by ...
x² -2x -2/7 = 0 . . . . . divide by 7
x² -2x +1 -9/7 = 0 . . . . add and subtract 1
(x -1)² = 9/7 . . . . . . . . . . write as a square, add 9/7
x -1 = ±√(9·7/49) = ±(3/7)√7 . . . . take the square root
x = 1 ± (3/7)√7
b) (x² - ...Rational inequalities are best solved by identifying the roots of numerator and denominator. These tell you where the function changes sign. The end behavior of the rational function tells you what the signs are changing from.
\(\dfrac{x^2-4x-12}{x^2-25}\ge 0\\\\\\\dfrac{(x+2)(x-6)}{(x+5)(x-5)}\ge0\)
This has a horizontal asymptote at y=1 for |x|→∞. It has vertical asymptotes at x=±5.
The sign changes occur at x ∈ {-5, -2, 5, 6}. The rational expression is positive (approaching +1) for x < -5 and for x > 6. It is negative in the adjacent intervals, so positive again for -2 < x < 5.
The inequality is satisfied for ...
x < -5-2 ≤ x < 56 ≤ xis it possible for an object to have no (zero) momentum? use the mathematical definition of momentum (p
Answers
Yes, it is possible for an object to have zero momentum. Momentum is defined as function the product of mass and velocity, so an object with zero mass or zero velocity will have zero momentum.
Momentum is a physical property of an object that is equal to the product of its mass and velocity. It is measured in kilogram meters per second (kg m/s) and is a vector quantity, meaning it has both magnitude and direction. In order for an object to have zero momentum, it must have either zero mass or zero velocity. An object with zero mass will always have zero momentum regardless of its velocity, while an object with zero velocity will only have zero momentum if its mass is also zero. An object with nonzero mass but zero velocity still has nonzero momentum if its mass is not zero. Therefore, it is possible for an object to have zero momentum.
Learn more about function here
https://brainly.com/question/29633660
#SPJ4
the complete question is
is it possible for an object to have no (zero) momentum? use the mathematical definition of momentum (p) to explain
It is possible for an object to have No (Zero) momentum because Momentum is the product of mass and velocity, so the object with zero mass or zero velocity will have No momentum.
What is Momentum ?
The Momentum of an object is a vector quantity that is defined as the product of the mass and velocity , the unit of measurement if Kg m/s .
So , for the object to have No (zero) momentum, the object must have either zero mass or zero velocity. that means the object with zero mass will always have No (zero) momentum regardless of velocity of the object ,
whereas the object with 0 velocity will only have No (zero) momentum if the mass is also 0 .
Therefore , By the Mathematical Definition of momentum , Yes , it is possible for the object to have No(zero) momentum .
Learn more about Momentum here
https://brainly.com/question/8635369
#SPJ4
Toula owns the Pita Pan restaurant. She needs to order supplies for the upcoming weekend rush. She needs 150 bags of pita bread. The bread come in crates of 50, and each crate costs $15.00. She also needs 65 containers of hummus dip. There are 5 containers in a box, and each box costs $20.00 What expressions can Toula use to determine how much the pita bread and hummus dips will cost? What will the total be?
Answers
The total cost of the pita bread and hummus dips will be $305.00.
To determine the cost of the pita bread and hummus dips, Toula can use the following expressions:
Cost of pita bread:
Number of crates needed = (150 bags) / (50 bags/crate) = 3 crates
Cost of each crate = $15.00
Total cost of pita bread = (Number of crates needed) × (Cost of each crate) = 3 crates × $15.00/crate = $45.00
Cost of hummus dips:
Number of boxes needed = (65 containers) / (5 containers/box) = 13 boxes
Cost of each box = $20.00
Total cost of hummus dips = (Number of boxes needed) × (Cost of each box) = 13 boxes × $20.00/box = $260.00
Therefore, the expressions Toula can use to determine the costs are:
Cost of pita bread = 3 crates × $15.00/crate
Cost of hummus dips = 13 boxes × $20.00/box
The total cost will be the sum of the costs of pita bread and hummus dips:
Total cost = Cost of pita bread + Cost of hummus dips
Total cost = $45.00 + $260.00
Total cost = $305.00
Therefore, the total cost of the pita bread and hummus dips will be $305.00.
for such more question on cost
https://brainly.com/question/8993267
#SPJ8
N
50°
AOMN~ ARPQ
Find 0.
M
Ө
0 = [?]°
<
P
70°
R
![N50AOMN~ ARPQFind 0.M0 = [?]<P70R](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/veKTlRrJcwtcPEhjGPeUEj7WPgDpy10G.png)
Answers
Answer:
60°
Step-by-step explanation:
In similar triangles, the corresponding angles are congruent.
∠O = R
O = 70°
In ΔOMN,
∠O + ∠M + ∠N = 180 {Angle sum property of triangle}
70 + 50 + Ф = 180
120 + Ф = 180
Subtract 120 from both sides,
Ф = 180 - 120
Ф = 60°
derivate (cos(3x^2). (5x^3 -1)^1/3 +sin 4x^3)^4
\( \: \: \: \: find \: first \: derivative \\ ( cos(3x {}^{2} ) \times ( \sqrt[3]{5x {}^{3} - 1} ) + \sin(4x {}^{3} ) {}^{4} \)
Answers
Answer:
Step-by-step explanation:
\(\frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^4\\\\=4[cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^3\; \frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)] --- eq(1)\)
Lets look at the derivative part:
\(\frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)] \\\\= \frac{d}{dx}[cos(3x^2) \sqrt[3]{5x^3 -1} ] + \frac{d}{dx}[sin(4x^3)]\\\\=cos(3x^2) \frac{d}{dx}[ \sqrt[3]{5x^3 -1} ] + \sqrt[3]{5x^3 -1}\frac{d}{dx}[ cos(3x^2) ] + cos(4x^3) \frac{d}{dx}[4x^3]\\\\=cos(3x^2) \frac{1}{3} (5x^3 -1)^{\frac{1}{3} -1} \frac{d}{dx}[5x^3 -1] + \sqrt[3]{5x^3 -1} (-sin(3x^2))\frac{d}{dx}[ 3x^2] + cos(4x^3)[(4)(3)x^2]\)
\(=\frac{cos(3x^2) 5(3)x^2}{3(5x^3 - 1)^{\frac{2}{3} }} -\sqrt[3]{5x^3 -1}\; sin(3x^2) (3)(2)x + 12x^2 cos(4x^3)\\\\=\frac{5x^2cos(3x^2) }{(5x^3 - 1)^{\frac{2}{3} }} -6x\sqrt[3]{5x^3 -1}\; sin(3x^2) + 12x^2 cos(4x^3)\)
Substituting in eq(1), we have:
\(\frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^4\\\\=4[cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^3\; [\frac{5x^2cos(3x^2) }{(5x^3 - 1)^{\frac{2}{3} }} -6x\sqrt[3]{5x^3 -1}\; sin(3x^2) + 12x^2 cos(4x^3)]\)
What is the determinant of the coefficient matrix of the system?
–158
–117
65
117
Answers
Answer:
C
Step-by-step explanation:
I got 100% on EDGE 2020 Unit test
Answer:
C. 65
Explanation:
Hope you have a great day!
cement
For each year, the population of a forest of trees is
represented by A(t) = 115(1.025)' In a neighboring forest,
the population of the same type of tree is represented by
the function B(t) = 82(1.029)".
s
ments
5
Assuming the population growth models continue to
represent the growth of the forests, which forest will have a
greater number of trees after 20 years? By how many?
Answers
Answer: Forest A will have a greater tree population
Step-by-step explanation: The function for forest A is A(t)=115(1.025), which is the number of trees in one year, so a formula to calculate for t number of years could be: A(t) = 115(1.025)(t), and for B it could be B(t) = 82(1.029)(t).
t represents the number of years, so after 20 years the number of trees would be:
A(20) = 115(1.025)(20) = 2357.5
B(20) = 82(1.029)(20) = 1687.56
A(20 - B(20) => 2357.5 - 1687.56 = 669.94
Therefore, there would be a greater number of trees in Forest A after 20 years. It is greater than forest B by 669.94 trees.
3. A-line segment has endpoints A(–2, 3) and B(6, –1):
i) Outline your strategy for finding the equation of its perpendicular bisector. (3C)
ii) Carry out the strategy and find the equation of its perpendicular bisector. (3T)
Answers
The equation of the segments perpendicular bisector is; y = -¹/₂x + 2
How to find the equation of the perpendicular bisector?i) Since it is a perpendicular bisector, hence point M is the midpoint. Thus;
Midpoint (AB) = [(x₁ + x₂)/2], [(y₁ + y₂)/2] = (x_m, y_m)
Slope AB will be;
m₁ = ((x₁ - x₂)/(y₁ - y₂))
Slope of perpendicular bisector is;
m₂ = -1/m₁
Equation of perpendicular bisector is;
(y - y_m) = m₂(x - x_m)
ii) Midpoint (AB) = [(-2 + 6)/2], [(3 - 1)/2] = (2, 1)
Slope AB will be;
m₁ = ((6 + 2)/(-1 - 3)) = -2
m₂ = -1/-2 = 1/2
Equation of perpendicular bisector is;
(y - 1) = -¹/₂(x - 2)
y - 1 = -¹/₂x + 1
y = -¹/₂x + 2
Read more about Perpendicular bisector at; https://brainly.com/question/11006922
#SPJ1
help will give brainliest

Answers
Answer:
B
Step-by-step explanation:
2/5 is equal to 40 percent
Is an example of money
Answers
Answer:
Gold coins are an example of commodity money. ... Dollar bills are an example of fiat money because their value as slips of printed paper is less than their value as money. Bank money consists of the book credit that banks extend to their depositors.
Step-by-step explanation:
The amount of time it takes Isabella to wait for the bus is continuous and uniformly distributed between 4 minutes and 18 minutes. What is the probability that it takes Isabella more than 7 minutes to wait for the bus
Answers
Answer:
0.25 or 25% probability
Step-by-step explanation:
The lower limit in this question = a
The upper limit = b
P(X<=x) = x-a/b-a
a = 4
b = 8
The question says it is uniformly distributed between 4 minutes and 8 minutes
Probability that it takes her more than 7 minutes to wait for the bus
P(X<=7) + P(X>7)= 1
We are to get P(X>7)
= 1 - (7-4/8-4)
= 1-3/4
= 1-0.75
= 0.25
= 25% probability it takes her more than 7 minutes to wait
What’s the answer to this problem

Answers
Answer:
1.2075
Step-by-step explanation:
Multiply the speed of the turtle ( 0.69 miles per hour) by the number of hours it takes ( 1.75 hours)
Answer: 1.2075
Step-by-step explanation:
multiply 0.69*1.75 and u will get 1.2075
Solve 3^5x=10
HELP PLS
Answers
Answer:
x = 10/243
Step-by-step explanation:
3^5x = 10
243x = 10
Divide 243 on both sides
10/243
Answer ASAP but only if you are SURE about it
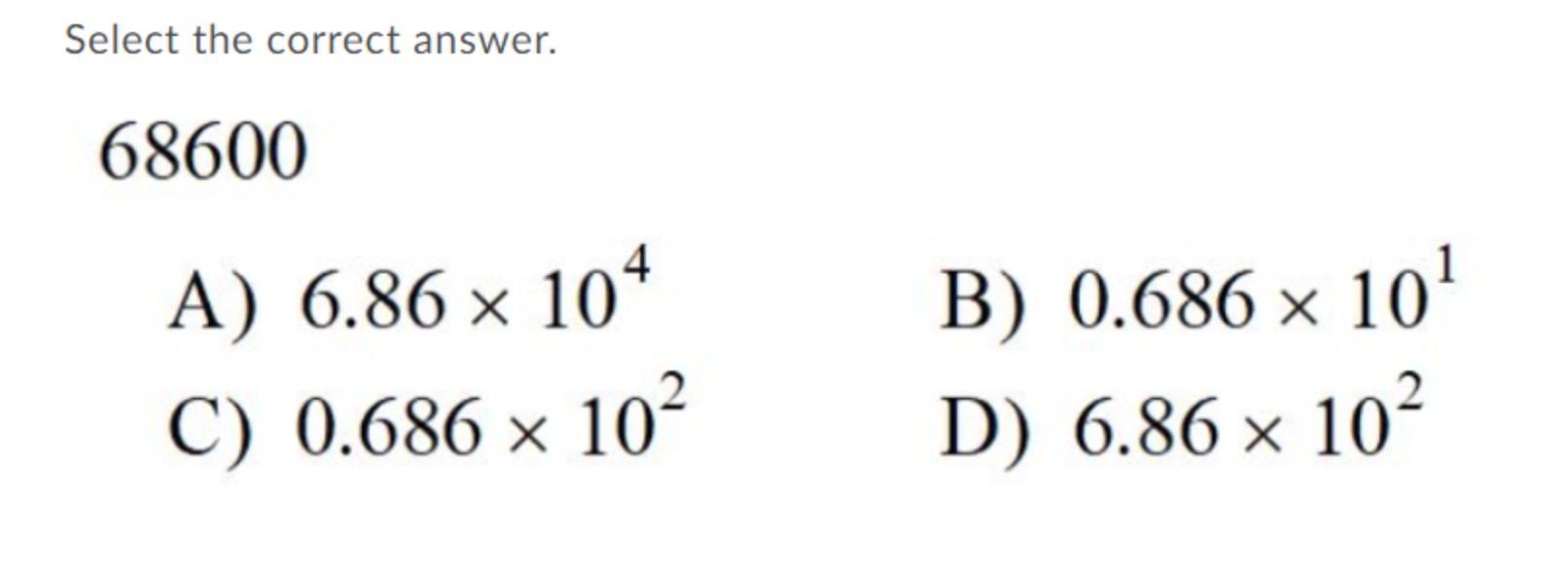
Answers
Answer:
It's A, 6.86 × 10⁴
Step-by-step explanation:
In scientific notation, you have the base, and the 10. The 10 is represented next to an exponent, whereas the base is a whole number and a decimal. If the decimal is moved right, the exponent following the 10 becomes negative. Left, it becomes positive. In this instance, the decimal is being moved left, thus the exponent is positive.
Answer:
A
Step-by-step explanation:
All my work is provided in the attached Screenshot! :)

William opened two investment accounts. The first year, these investments, which totaled $2600, yielded $175 in simple interest. Part of the money was invested at 7.5% and the rest at 5%. How much was invested at each rate?
Answers
An amount of $1800 was invested at a rate of 7.5% and $800 was invested at a rate of 5%.
What is the percentage?The percentage is a ratio that can be expressed as a fraction of 100.
Given that, one part of $2600 was invested at a rate of 7.5% and the other part was invested at a rate of 5%, and the total yield was $175 simple interest.
Let $x was invested at 7.5%, then $(2600-x) was invested at 5%.
Since the yield is $175, it follows,
7.5% of x + 5% of (2600-x) = 175
7.5x/100 + 5(2600-x)/100 = 175
7.5x + 13000 - 5x = 17500
2.5x = 17500-13000
2.5x = 4500
x = 1800
Now, the value of (2600-x) is,
2600-1800
=800
Hence, $1800 was invested at a rate of 7.5% and $800 was invested at a rate of 5%.
Learn more on percentages here:
https://brainly.com/question/14979505
#SPJ1
William invested $1800 at 7.5% and $800 at 5% on his both accounts.
What is simple interest?We know simple interest (SI) is given by SI = (p×r×t)/100, where
p = principle, r = rate in percentage, and t = time in years.
Given, William opened two investment accounts. In the first year, these investments, which totaled $2600,
Assuming he invested $x at 7.5% on the first account and $(2600 - x) at 5% in the second account and yielded $175 in simple interest.
∴ (x×7.5×1)/100 + {(2600 - x)×5×1}/100 = 175.
7.5x/100 + (13000 - 5x)/100 = 175.
7.5x + 13000 - 5x = 17500.
2.5x = 4500.
x = 1800. And (2600 - x) = (2600 - 1800) = 800.
learn more about simple interests here :
https://brainly.com/question/11564235
60 POINTS ANSWER FOR BRAINLIST AND HEARTS

Answers
Answer:
a. The given equation is (y - 3)^2 -10 = 71. To determine the number and type of solutions, we need to use the discriminant, which is given by b^2 - 4ac, where a, b, and c are the coefficients of the quadratic equation in standard form (ax^2 + bx + c = 0). In this case, the equation can be rewritten as (y - 3)^2 = 81, which is in the form of (y - k)^2 = r^2, where k = 3 and r = 9. Therefore, the equation can be written as (y - k)^2 - r^2 = 0, which is a quadratic equation with a = 1, b = -6, and c = -72. The discriminant is then b^2 - 4ac = (-6)^2 - 4(1)(-72) = 300. Since the discriminant is positive, there are two real solutions.
b. To solve the equation (y - 3)^2 -10 = 71, we first add 10 to both sides to get (y - 3)^2 = 81. Then, we take the square root of both sides to get y - 3 = ±9. Adding 3 to both sides, we get y = 3 ± 9, which gives us two solutions: y = 12 and y = -6.
Therefore, the equation (y - 3)^2 -10 = 71 has two real solutions, which are y = 12 and y = -6.
Step-by-step explanation:
Answer: type: real number of solutions:2 y=12,-6
Step-by-step explanation:
see images for explanations


Help? Please…………………..

Answers
Answer:
constant monomial
Step-by-step explanation:
the 8 is a constant number and has one term.

the product of two and a number, divided by five 5
Answers
The expression of the given statement is \(\frac{2x}{5}\) .
What is algebraic expression?
When terms are combined using operations like addition, subtraction, multiplication, division, etc., the result is an algebraic expression (or variable expression). Let's look at the formula 5x + 7 as an illustration. Consequently, we can state that 5x + 7 is an illustration of an algebraic statement. Here are some more examples: 5x + 4y + 10
Here the given product of two and a number. Lets us take number as x. Then ,
=> 2*x= 2x
Product of two and a number divided by 5. Then,
=> \(\frac{2x}{5}\)
Hence the algebraic expression of the given statement is \(\frac{2x}{5}\) .
To learn more about algebraic expression refer the below link
https://brainly.com/question/4344214
#SPJ1
What is the standard form equation of an ellipse that has vertices (−2,14) and (−2,−12) and co-vertices (9,1) and (−13,1)?
Answers
Answer:
\(\frac{(x+2)^2}{121} + \frac{(y-1)^2}{169} = 1\)
Step-by-step explanation:
First, we identify that the vertices are vertical.
(an image below is attached if you want to see a visualization)
Therefore, the equation is such:
\(\frac{(x-h)^2}{b^2} + \frac{(y-k)^2}{a^2} = 1\)
(h,k) is the center of the ellipse, which we could easily calculate by finding the midpoint between any pair of vertices.
This gets us (-2, 1)
Therefore, h = -2, k = 1
Now we want to find a,
we know the length of the major axis is 2a, and in this case, our length of the major axis is 26. So a = 13
Now we want to find b,
We know the length of the minor axis is 2b, and in this case, our length is 22, so b = 11
Now we will just plug in all the values and simplify to get our answer! B)

Graph the equation by plotting three
points. If all three are correct, the line
will appear.
-y = x + 1
Answers
Answer:x=−y−1
Step-by-step explanation:Let's solve for x.
−y=x+1
Step 1: Flip the equation.
x+1=−y
Step 2: Add -1 to both sides.
x+1+−1=−y+−1
x=−y−1
Answer:
x=−y−1
Please answer this correctly

