What is on way feudal japan was different than feudal Europe???? Not mathematics it is history.

Answers
Related Questions
The perimeter of the triangle below is 54 units. Find the value of y.

Answers
Answer:
y = 7
Step-by-step explanation:
3y + (y+1) + (4y-3) = 54
3y + y + 4y + 1 - 3 = 54
8y - 2 = 54
8y = 54 + 2
8y = 56
y = 56/8
y = 7
Check:
3*7 + (7+1) + ((4*7)-3) = 54
21 + 8 + 28-3 = 54
29 + 25 = 54
so for this answer we have to give our answers to the 4 decimal places if it is necessary

Answers
A shirt costs ₹(a2 –ab -b2 ) , a pair of trousers cost ₹(2a2 +8ab-2b2 ) and a pair of shoes cost ₹(a2 –3ab+4b2 ) .After collecting these three items from the store, Ranjan paid ₹(2a+b )2 .What balance will Ranjan receive from the cashier ?
Answers
The balance Ranjan will receive from the cashier is ₹ 0
How to determine the balanceBased on the information given, we have that;
shirt costs ₹(a² –ab -b² ) pair of trousers cost ₹(2a² +8ab-2b² ) pair of shoes cost ₹(a² –3ab + 4b² ) Ranjan paid ₹(2a+b )2Now, expand the bracket for the payment, we have;
(2a+b )²
(2a +b) (2a + b)
Multiply through
4a² + 2ab + 2ab + b²
Add like terms
4a² + 4ab + b²
Now, let's add the amount for the items bought
a² –ab -b² + 2a² +8ab-2b² + a² –3ab + 4b²
add like terms
4a² + 4ab + b²
Now, subtract the amounts
4a² + 4ab + b² - 4a² + 4ab + b²
₹ 0
Hence, the balance is ₹ 0
Learn more about cost here:
https://brainly.com/question/19104371
#SPJ1
What might you expect to find out about people who are described as credit risks?
Answers
Solve for y.
8
= -7
y +7
Simplify your answer as much as possible.
y = 0
No
solution
3
X Х
?

Answers
Answer:
y=−1/7
for the picture is y=-57/7
Step-by-step explanation:
1. 8= -7y +7Switch:sides
-7y+7=8
subtract 7 from both sides
-7y=1
divide both sides by -7
y=−1/7
2.so for 8/y+7=-7multiply both sides by (y+7)
8/y+7(y+7)=-7(y+7)
simplify 8=-7(y+7)
flip
-7(y+7)=8
divide both sides by -7
y+7=-8/7
subtract 7 from both sides
and simplify
y=-57/7
In an episode of the old school version of the game show Family Feud, 43 out of a random sample of 100 people said they pick their noses at red lights. Find a 95% confidence interval of the proportion of all people who pick their noses at red lights.
Answers
Answer:
95% of confidence interval of the proportion of all people who pick their noses at red lights
(0.3342 , 0.5258)
Step-by-step explanation:
Step(i):-
Given sample size 'n' = 100
Given data 43 out of a random sample of 100 people said they pick their noses at red lights.
sample proportion
\(p^{-} = \frac{x}{n} = \frac{43}{100} = 0.43\)
Level of significance = 0.05
Z₀.₀₅ = 1.96
Step(ii):-
95% of confidence interval of the proportion of all people who pick their noses at red lights
\((p^{-} -Z_{\alpha } \sqrt{\frac{p(1-p)}{n} } ,p^{-} +Z_{\alpha } \sqrt{\frac{p(1-p)}{n} })\)
\((0.43 -1.96 \sqrt{\frac{0.43(1-0.43)}{100} } ,0.43 +1.96 \sqrt{\frac{0.43(1-0.43)}{100} })\)
( 0.43 - 0.0958 , 0.43 + 0.0958)
(0.3342 , 0.5258)
Conclusion:-
95% of confidence interval of the proportion of all people who pick their noses at red lights
(0.3342 , 0.5258)
Lori read the total of 48 pages over 3 hours
Answers
Answer:
16 pages per hour
Step-by-step explanation:
48 ÷ 2 = 16 pages per hour
Given that the triangles shown below are simiar, what is the value of x?
O A. 7.1
O B. 5
O C. 14
O D. 10

Answers
Answer:
C) 14
Step-by-step explanation:
Both triangles are the same as far as angles, DEF is however half of ABC. Therefore x is half of 28
Find a vector equation and parametric equations for the line The line through the point (2, 2.4, 3.5) and parallel to the vector 3i 1 2j 2 k
Answers
Answer:
The vector equation
\(r = (2 + 3t)i+ (2.4 + 2t)j+ (3.5 - t)k\)
The parametric equation
\(x = 2 + 3t\\y = 2.4 + 2t\\z = 3.5-t\)
Step-by-step explanation:
Given
\(Point = (2,2.4,3.5)\)
\(Vector = 3i + 2j - k\)
Required
The vector equation
First, we calculate the position vector of the point.
This is represented as:
\(r_0 = 2i + 2.4j + 3.5k\)
The vector equation is then calculated as:
\(r = r_o + t * Vector\)
\(r = 2i + 2.4j + 3.5k + t * (3i + 2j - k)\)
Open bracket
\(r = 2i + 2.4j + 3.5k + 3ti + 2tj - tk\)
Collect like terms
\(r = 2i + 3ti+ 2.4j + 2tj+ 3.5k - tk\)
Factorize
\(r = (2 + 3t)i+ (2.4 + 2t)j+ (3.5 - t)k\)
The parametric equation is represented as:
\(x = x_0 + at\\y = y_0 + bt\\z = z_0 + ct\)
Where
\(r = (x_0 + at)i +(y_0 + bt)j+(z_0 + ct)k\)
By comparison:
\(x = 2 + 3t\\y = 2.4 + 2t\\z = 3.5-t\)
Kadeem has $50,000 in an account that compounds interest sem-annually at a rate of 1.8%. He withdraws $5,000 semiannually from the account
Will his money last:
4.5 years (yes or no), 5 years (yes or no), 5.5 years (yes or no), 6 years (yes or no)
Answers
The time taken is 5.3 years.
What is Compound Interest?Compound interest simply refers to the fact that an investment, loan, or bank account's interest accrues exponentially over time as opposed to linearly over time. The word "compound" is crucial here.
Compound interest is when you receive interest on both your interest income and your savings.
Given:
P = 50, 000
W= 5000
r= 1.8%= 0.018
n= 2
Using, P = W (1- \((1+ r/n)^{-nt}\)) / (r/n)
Putting all the values we get
P = W (1- \((1+ r/n)^{-nt}\)) / (r/n)
50000 = 5000 (1- \((1+0.018/2)^{-2t}\)) / (0.018/2)
10 = (1- \((1+0.009)^{-2t}\)) / (0.009)
0.09 = 1 - \((1.009)^{-2t\)
\((1.009)^{-2t\) = 0.91
Taking log on both side
-2t log 1.009 = log 0.91
t= log 0.91/ (log 0.091) / (-20
t= 5.3
Learn more about Compound Interest here:
https://brainly.com/question/14295570
#SPJ1
Help please:)
Graph the equation by plotting points.
X=4
Answers
Answer:
(4,0)
Step-by-step explanation:
You basically are plotting a point on the positive number 4 on the x line. Since they're only asking for an X and not a Y, you'd leave it as (4,0). Hope this helps!
Find all solutions
for cotx=-1
Answers
Answer:
\(\cot(x) = -1\) whenever \(\displaystyle x = k\, \pi-\frac{\pi}{4}\) radians, where \(k\) could be any integer (\(k \in \mathbb{Z}\), which includes positive whole numbers, negative whole numbers, and zero.)
Step-by-step explanation:
\(x = 45^\circ\) (as in isoscele right triangles) would ensure that \(\displaystyle \cot(x) = 1\). Since cotangent is an odd function, \(\cot(-45^\circ) = -1\).
Equivalently, when the angles are expressed in radians, \(\cot(-\pi / 4) = -1\).
The cycle of cotangent is \(\pi\) (or equivalently, \(180^\circ\).) Therefore, if \(k\) represents an integer, adding \(k\, \pi\) to the input to cotangent would not change the output. In other words:
\(\displaystyle \cot\left(k\, \pi - \frac{\pi}{4}\right) = \cot(-\pi / 4) = -1\).
Hence, \(\displaystyle x = k\, \pi-\frac{\pi}{4}\) would be a solution to \(\cot(x) = -1\) whenever \(k\) is an integer.
Since \((-\pi / 4)\) is the only solution to this equation in the period \((0,\, \pi)\), all real solutions to this equation would be in the form \(\displaystyle x = k\, \pi-\frac{\pi}{4}\) (where \(k\) is an integer.)
√√96
√8
Ο 213
Ο 4
Ο 222
D. 12

Answers
Answer:
2sqr3, the first option
Step-by-step explanation:
What is closest to the slope of the line graphed above?
0-1/3
0-3
O 3
1/3
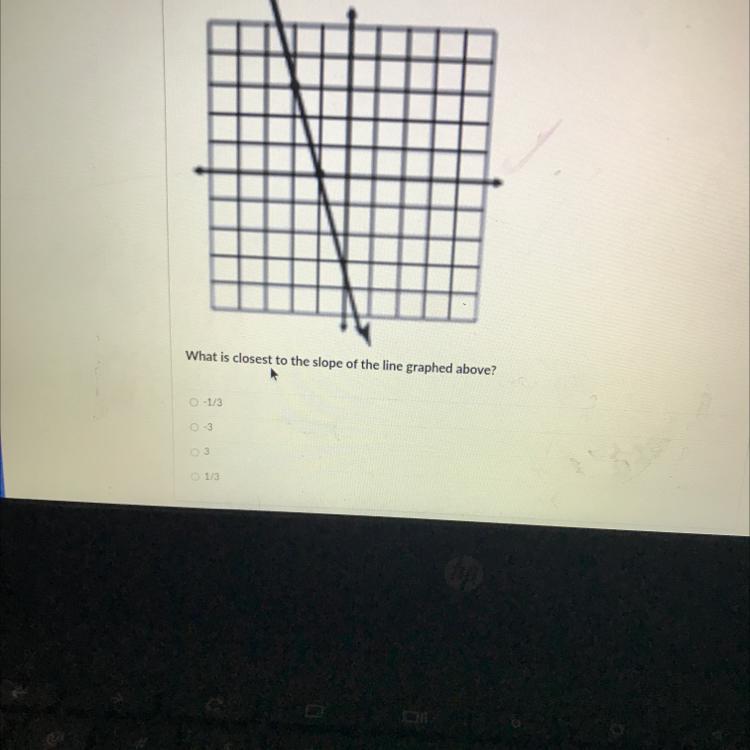
Answers
So second to last
Explanation: I hope this helps
The Answer would be -3
Rise over run.
From one point to another the graph rises 3 and moves left 1.
Given a random sample: X= 75, Sx = 24, and n = 36. Construct a 95% confidence interval and
estimate the population mean, m.
What would be the answer to this?
Answers
we estimate the population mean m to be 75.
What is confidence interval?
A confidence interval (CI) for an unknown parameter in frequentist statistics is a range of estimations. The most popular confidence level is 95%, but other levels, such 90% or 99%, are occasionally used for computing confidence intervals. The fraction of related CIs over the long run that actually contain the parameter's true value is what is meant by the confidence level. The degree of confidence, sample size, and sample variability are all factors that might affect the width of the CI. A larger sample would result in a narrower confidence interval if all other factors remained constant. A wider confidence interval would also be required by a higher confidence level and would be produced by a sample with more variability.
Since we want a 95% confidence interval, α = 0.05/2 = 0.025 and we need to find the critical value from the t-distribution with (36-1) = 35 degrees of freedom. Using a t-table or calculator, we find that t0.025,35 = 2.032.
Now, plugging in the values we have:
CI = 75 ± (2.032 * (24/√36))
CI = 75 ± (2.032 * 4)
CI = 75 ± 8.128
So the 95% confidence interval for the population mean m is (66.872, 83.128). This means we are 95% confident that the true population mean falls within this interval.
As for the estimated population mean, we can simply take the sample mean, which is X = 75.
Therefore, we estimate the population mean m to be 75.
Learn more about confidence interval, by the following link.
https://brainly.com/question/17097944
#SPJ9
A swim coach randomly elects 3 swimmers from a team of 8 to swim in a heat. What is the probability that she will choose the three strongest swimmers?
Answers
Answer:
Probability= 0.375
Step-by-step explanation:
Probabilty is the chance or possiblity of an event occuring.
In an event we should have a total possible space and a specific expected outcome.
In this scenario we have 8 possible sample space and 3 expected outcome.
The probability of selecting the strongest= 3/8
Probability= 0.375
How do you solve this?
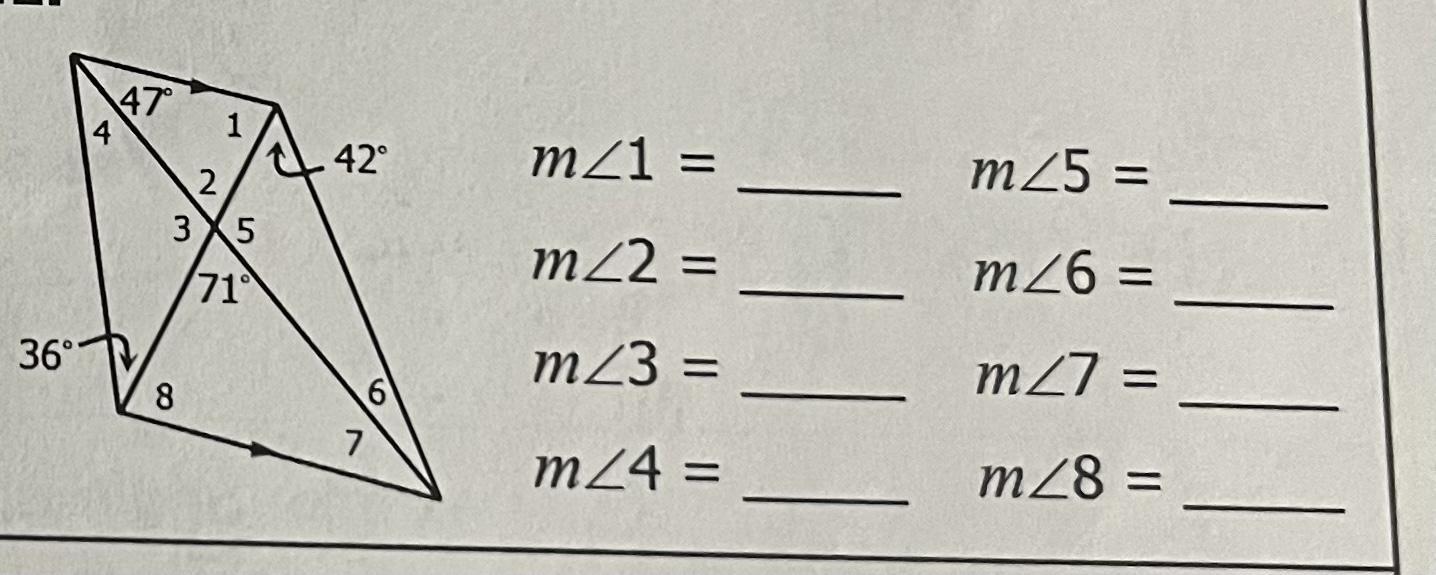
Answers
The measures of the angles are:
m<7 = 47°
m<8 = 62°
m<1 = 62°
m<2 = 71° [vertical angles theorem]
m<5 = 109°
m<3 = 109°
m<4 = 35°
m<6 = 29°
What is the Alternate Interior Angles Theorem?The alternate interior angles theorem states that two interior angles that are formed along a transversal and lie alternate to each other on two parallel lines are congruent to each other.
Measure of angle 7 = 47° [based on the alternate interior angles theorem]
Measure of angle 8 = 180 - 47 - 71 [triangle sum theorem]
Measure of angle 8 = 62°
Measure of angle 1 = measure of angle 8 = 62° [based on the alternate interior angles theorem]
Measure of angle 1 = 62°
Measure of angle 2 = 71° [vertical angles theorem]
Measure of angle 5 = 180 - 71 [linear angle theorem]
Measure of angle 5 = 109°
Measure of angle 3 = measure of angle 5 = 109° [vertical angles theorem]
Measure of angle 4 = 180 - measure of angle 3 - 36 [linear angle theorem]
Measure of angle 4 = 180 - 109 - 36
Measure of angle 4 = 35°
Measure of angle 6 = 180 - measure of angle 5 - 42 [linear angle theorem]
Measure of angle 6 = 180 - 109 - 42
Measure of angle 6 = 29°
Learn more about the alternate interior angles theorem on:
https://brainly.com/question/24839702
#SPJ1
The solution to X +9-3 is less than or equal to 14
Answers
Answer:
\(x∈( - ∞;8]\)
Step-by-step explanation:
\(x + 9 - 3 \leqslant 14\)
Collect like-terms:
\(x \leqslant 14 - 9 + 3\)
\(x \leqslant 8\)
\(x∈( - ∞;8]\)
If 9x - 3y = -10 and 3x - 4y = 1 are true equations, what would be the value
of 12x-7y?
Answers
Answer:
Step-by-step explanation:
9x-3y=-10 ...............(1)
3x-4y=1...............(2)
multiplying equation (2) by 3
9x-12y=3...................(3)
Using elimination method, then
9x-3y=-10 ...............(1)
9x-12y=3...................(3
9y= -13
y= -13/9
substituting y= -13/9 in equation (1) then
9x-3(-13/9)= -10
9x+13/3= -10
multiplying throughout by 3
27x+13= -30
27x= -30-13
27x= -43
x= -43/27
since x and y values are known, then
12x-7y = 12(-43/27) - 7(-13/9)
12x-7y = -516/27 + 91/9
12x-7y = -9
16) Graph g(x) = x + 3 + 2

Answers
HELP!!! A set of 3 cards, spelling the word ADD, are placed face down on the table. Determine P(D, D) if two cards are randomly selected with replacement.
1/3
2/3
2/6
4/9
Answers
number of favourable outcome to d is 2
number of possible outcome is 3
p(D)=2/3
p(D, D) =p(D)×p(D)
p(D,D) 2/3 ×2/3
p(D,D)=4/9
probability =4/9 (D)
Floyd builds rectangles using matches, as shown below. When the length of the rectangle is 3 matches, he used 8 matches. When the length of the rectangle is 7 matches, he used 16 matches. How many matches does Floyd need to make a rectangle with length 20 matches? [Type in only o numeric digit as your answer with no spaces Answer: Search Q
Answers
Floyd needs 33 matches to make a rectangle with a length of 20 matches.
To find out how many matches Floyd needs to make a rectangle with a length of 20 matches, we can observe a pattern in the given information.
From the given data, we can see that as the length of the rectangle increases by 4 matches, the number of matches used increases by 8. This means that for every additional 4 matches in length, Floyd requires 8 more matches.
Using this pattern, we can calculate the number of matches needed for a rectangle with a length of 20 matches.
First, we need to determine the number of 4-match increments in the length of 20 matches. We can do this by subtracting the starting length of 3 matches from the target length of 20 matches, which gives us 20 - 3 = 17.
Next, we divide the number of 4-match increments by 4 to determine how many times Floyd needs to add 4 matches. In this case, 17 ÷ 4 = 4 with a remainder of 1.
Since Floyd requires 8 matches for each 4-match increment, we multiply the number of increments by 8, which gives us 4 × 8 = 32 matches.
Finally, we add the remaining matches (1 match in this case) to the total, resulting in 32 + 1 = 33 matches needed to reach a length of 20 matches.
For more such questions on rectangle, click on:
https://brainly.com/question/2607596
#SPJ8
In a class of 32 students for students were home sick with the flu on Thursday what percent of the students were absent on Thursday
Answers
Explanation: You have to divide the numerator (4) by the denominator (32), and move the decimal point two places to the right to change from a decimal to a percentage.
4 ÷ 32 = 0.125 (or 12.5%)
Question 6 Clare volunteers at a local library during the summer. Her work includes putting labels on 750 books. How many minutes will she need to finish labeling all books if she takes no breaks and labels 15 books a minute Question 7 Suppose Clare labels the books at a constant speed of x books per minute. Write an equation that represents the relationship between her labeling speed and the number of minutes it would take her to finish labeling.
Answers
Clare is going to need 50 minutes to label 750 books
1) Gathering the data
750 books
15 books per minute
2) Let's set a proportion for that, considering the fact that her speed is constant
15 books ----------------------1 minute
750 -------------------------------x
15x = 750
x= 50 books
3) Clare is going to need 50 minutes to label 750 books.
Giving brainly
Sienna's height is 5 inches less than her brother's height.
Her brother's height is unknown.
Which expression shows Sienna's height? Use x for her brother's height.
O A.
B. x+ 5
C. X-5
D. 5x

Answers
125x ^ 3 - 27 = 0
Solve this by grouping
Answers
The solution to the equation 125x³ - 27 = 0 is (5x−3)(25x ^2 +15x+9)
What is an equation?An equation is a mathematical expression that contains an equals symbol. Equations often contain algebra. Algebra is used in mathematics when you do not know the exact number in a calculationsolving the equation 125x³ - 27 = 0 by grouping
Rewriting 125x^ 3 −27 as (5x) ^3 −3³
The difference of cubes can be factored using the rule:: a ^3 −b^ 3 =(a−b)(a^ 2 +ab+b^ 2 )
Polynomial 25x^ 2 +15x+9 is not factored since it does not have any rational roots.
Hence, (5x−3)(25x ^2 +15x+9)
Learn more about equation at:
https://brainly.com/question/25976025
#SPJ1
complete the sentence. a(n) equation is a mathematical statement that shows two expressions are equal using an equal sign.
Answers
A mathematical statement in that shows two statements are equal is known as an equation (where two statements are separated by equals to "=" sign)
A mathematical statement in which the equal sign is applied to demonstrate equivalence between a number or expression along one side of the equal sign and a number or expression on the other side of the equal sign is known as an equation. There are two sides to every equation (i.e., left and right).
Equivalent equations are expressions that perform despite the fact that they look different. If two algebraic expressions are equal, then the two expressions possess the same value when we substitute similar value(s) for the variable(s).
For more information on equations, visit :
https://brainly.com/question/16929479
#SPJ4
Determine the probability of rolling a die and getting a 2
then a 5.
Answers
The probability of rolling a die and getting a 2, then a 5, is 1/36.
To determine the probability of rolling a die and getting a 2, then a 5, we need to multiply the probabilities of each event happening.
First, let's consider the probability of rolling a die and getting a 2. Since there are six equally likely outcomes when rolling a fair six-sided die (numbers 1 to 6), the probability of rolling a 2 is 1/6.
Now, let's consider the probability of rolling a die and getting a 5. Again, there are six equally likely outcomes, so the probability of rolling a 5 is also 1/6.
To find the probability of both events happening, we multiply the probabilities:
Probability of rolling a 2 and then a 5 = (1/6) * (1/6) = 1/36.
Therefore, the probability of rolling a die and getting a 2, then a 5, is 1/36.
It's important to note that each roll of the die is an independent event, meaning that the outcome of one roll does not affect the outcome of the next roll. Therefore, the probability of rolling a 2 and then a 5 remains constant at 1/36 regardless of previous rolls or the order in which they occur.
For more such questions on probability visit:
https://brainly.com/question/251701
#SPJ8
write a question in y=a x b^x whose graph passes through the Coordinate points (2,12) and (3,24)
Answers
The graph of y = 3 x 2^x passes through the coordinate points (2,12) and (3,24).
To write a question in the form of y=a x b^x that passes through the coordinate points (2,12) and (3,24), we need to solve for the values of a and b.
First, let's substitute the coordinates (2,12) into the equation:
12 = a x b^2
Next, let's substitute the coordinates (3,24) into the equation:
24 = a x b^3
We now have two equations with two unknowns (a and b), which we can solve using algebra.
From the first equation, we can solve for a:
a = 12 / b^2
We can then substitute this value of a into the second equation:
24 = (12 / b^2) x b^3
Simplifying this equation, we get:
2 = b
We can then substitute this value of b back into the equation for a:
a = 12 / 2^2
a = 3
Therefore, the equation of the graph that passes through the coordinate points (2,12) and (3,24) is:
y = 3 x 2^x
We can check that this equation is correct by plugging in the coordinates:
When x = 2: y = 3 x 2^2 = 12
When x = 3: y = 3 x 2^3 = 24
To learn more about : graph
https://brainly.com/question/19040584
#SPJ11
Factorize a(a-b+c) - bc
Answers
a²-ab+ac-bc
a(a-b)+c(a-b)
(a-b)(a+c)