What is f(x)=x2-8x+11 written in vertex form
Answers
Related Questions
What is the equation of a line that passes through the point (2, −10) and is parallel to 14x+2y=6?
Answers
The the equation of a line that passes through the point (2, −10) and is parallel to 14x+2y=6 is 7x + y + 8 = 0.
A straight line is just a line with no curves. So, a line that extends to both sides till infinity and has no curves is called a straight line.
The equation of a line parallel to a given line will have the same slope as the given.
The equation of a line having a slope m and passing through the point (x', y') is written as
y - y' = m (x - x').
This is called point - slope equation of a straight line.
In the given equation,
14x+2y=6
⇒ 2y = -14x + 6
⇒ y = -7x + 3
Comparing it with standard equation of a straight line; y = m x + c, the slope m of the given line = -7
Therefore equation of the line parallel to the given line and passing through point (x', y') = (2, -10) would be:
y - (-10) = -7x + 2
⇒ y + 10 = -7x + 2
⇒ 7x + y + 8 = 0
Hence the required equation of line 7x + y + 8 = 0
To learn more about straight line visit:
brainly.com/question/27560536
#SPJ1
help pls I need itfb thanks

Answers
Answer:
19.98
Step-by-step explanation:
calculate
what do you need at least three points to define?
Answers
If you’re drawing the graph of a line, I tend to recommend plotting three points, not because you need three points to determine your line, but as a check. If you compute one point incorrectly it’s obvious something’s wrong when you plot them. If you make two mistakes you have to be pretty unlucky for the three to line up nicely. It still should be obvious something’s wrong.
4.1K views
Related Questions
The revenue of a car dealer from car sales is a function of the advertising expenditure. Hence R=f(a), where both of a and Rare in thousands of dollars. on advertising, then its revenue is 50 (a) f(10)=50 means that if the the car dealer spends 10 thousands of dollars thousands of dollars , spending on advertising, the car (b) f'(10)=2 means that for every increase of $1,000$ from 10 thousands of dollars dealer's revenue increases by about 2 thousands of dollars . (c) f(9.8) is approximate thousands of dollars .
Answers
a) "Revenue" refers to the income generated by the car dealer from car sales, and "expenditure" refers to the advertising spending. In this context, R=f(a) implies that the revenue (R) is a function of advertising expenditure (a), with both values measured in thousands of dollars.
b) f(10)=50 means that when the car dealer spends 10 thousand dollars on advertising, their revenue is 50 thousand dollars.
c) f'(10)=2 indicates that when the advertising expenditure is at 10 thousand dollars, an additional 1 thousand dollars spent on advertising will increase the car dealer's revenue by approximately 2 thousand dollars.
d) f(9.8) represents the car dealer's revenue in thousands of dollars when they spend 9.8 thousand dollars on advertising.
Based on the information provided, we can conclude that the revenue (R) of a car dealer is a function (f) of their advertising expenditure (a). Both R and a are measured in thousands of dollars.
Part (a) tells us that if the car dealer spends 10 thousand dollars on advertising (a = 10), their revenue will be 50 thousand dollars (R = 50). This means that f(10) = 50.
Part (b) gives us the derivative of the function f with respect to a. Specifically, it tells us that for every increase of $1,000 from an advertising expenditure of 10 thousand dollars, the dealer's revenue increases by about 2 thousand dollars. This can be written as f'(10) = 2.
Finally, part (c) asks us to find an approximate value for f(9.8). Since we don't have the exact functional form of f, we can't solve this exactly. However, we can make an estimate using the information we have.
From part (b), we know that f'(10) = 2, which means that the dealer's revenue increases by 2 thousand dollars for every 1 thousand dollar increase in advertising expenditure. So, if the dealer spends 9.8 thousand dollars on advertising, we can estimate that their revenue will be:
f(9.8) ≈ f(10) + (9.8 - 10) * f'(10)
f(9.8) ≈ 50 + (-0.2) * 2
f(9.8) ≈ 49.6
Therefore, an approximate value for f(9.8) is 49.6 thousand dollars.
Visit here to learn more about Revenue:
brainly.com/question/23706629
#SPJ11
What is the quotient of
7.584
×
1
0
6
7.584×10
6
and
7.9
×
1
0
2
7.9×10
2
expressed in scientific notation?
Answers
0.96×10⁴ is the quotient of 7.584×10⁶ and 7.9×10²
What is Division?A division is a process of splitting a specific amount into equal parts.
We need to find the quotient of
7.584×10⁶ and 7.9×10²
Dividend is the number that is to be divided by the divisor.
Divisor is the number by which the dividend is to be divided is called the divisor.
The resultant of the division is called the quotient.
7.584×10⁶/7.9×10²
0.96×10⁶⁻²
0.96×10⁴
Hence, 0.96×10⁴ is the quotient of 7.584×10⁶ and 7.9×10²
To learn more on Division click:
https://brainly.com/question/21416852
#SPJ1
Riley is building an ant farm for his school's science fair. He has enough materials to build a farm that is 726 square inches in total, 6 square inches of which will be taken up for food and water sources. Of the remaining available space, each ant needs at least 2 square inches to themselves. What is the maximum amount of ants Riley's ant farm can house?
Answers
I don't think I'm wrong but the answer 90
is the expression a valid way to calculate a 15% tip on a cab fare of d dollars?
Answer yes or no
EXPRESSION
0.10d + 0.05d Yes or No
0.85d Yes or No
1.015d Yes or No
0.15d Yes or no
Answers
Pls solve with all steps

Answers
The results of the expressions involving logarithms are listed below:
Case 1: 1 / 2
Case 2:
Subcase a: 0
Subcase b: 11 / 2
Subcase c: - 11 / 2
How to simplify and evaluate expressions involving logarithmsIn this problem we have a case of an expression involving logarithms that must be simplified and three cases of expressions involving logarithms that must be evaluated. Each case can be solved by means of the following logarithm properties:
㏒ₐ (b · c) = ㏒ₐ b + ㏒ₐ c
㏒ₐ (b / c) = ㏒ₐ b - ㏒ₐ c
㏒ₐ cᵇ = b · ㏒ₐ c
Now we proceed to determine the result of each case:
Case 1
㏒ ∛8 / ㏒ 4
(1 / 3) · ㏒ 8 / ㏒ 2²
(1 / 3) · ㏒ 2³ / (2 · ㏒ 2)
㏒ 2 / (2 · ㏒ 2)
1 / 2
Case 2:
Subcase a
㏒ [b / (100 · a · c)]
㏒ b - ㏒ (100 · a · c)
㏒ b - ㏒ 100 - ㏒ a - ㏒ c
3 - 2 - 2 + 1
0
Subcase b
㏒√[(a³ · b) / c²]
(1 / 2) · ㏒ [(a³ · b) / c²]
(1 / 2) · ㏒ (a³ · b) - (1 / 2) · ㏒ c²
(1 / 2) · ㏒ a³ + (1 / 2) · ㏒ b - ㏒ c
(3 / 2) · ㏒ a + (1 / 2) · ㏒ b - ㏒ c
(3 / 2) · 2 + (1 / 2) · 3 + 1
3 + 3 / 2 + 1
11 / 2
Subcase c
㏒ [(2 · a · √b) / (5 · c)]⁻¹
- ㏒ [(2 · a · √b) / (5 · c)]
- ㏒ (2 · a · √b) + ㏒ (5 · c)
- ㏒ 2 - ㏒ a - ㏒ √b + ㏒ 5 + ㏒ c
- ㏒ (2 · 5) - ㏒ a - (1 / 2) · ㏒ b + ㏒ c
- ㏒ 10 - ㏒ a - (1 / 2) · ㏒ b + ㏒ c
- 1 - 2 - (1 / 2) · 3 - 1
- 4 - 3 / 2
- 11 / 2
To learn more on logarithms: https://brainly.com/question/30226560
#SPJ1
Which of the binomials below is a factor of this trinomial?
-2x^2-22x+24
A. X + 1
B. X+4
C. X-4
D. X-1
Answers
The correct answer is option D.Which is ( x - 1 ).
What is a quadratic equation?
It is a polynomial with a degree of 2 or the maximum power of the variable is 2 in quadratic equations. It has two solutions as its maximum power is 2.
The solution of the given quadratic equation will be:-
-2x² - 22x + 24 = 0
x ² + 11x - 12 = 0
x² + 12x - x + 12 = 0
x ( x + 12 ) -1 ( x + 12 ) = 0
( x -1 ) ( x + 12 ) = 0
Therefore the correct answer is option D.Which is ( x - 1 ).
To know more about quadratic equations follow
https://brainly.com/question/1214333
#SPJ1
explain how u know what 1/3 of 2/5 is
Answers
Given that x = 15, and y = 60, determine which segments or
lines are parallel, and justify your solution.
Answers
Segments AB and CD are not parallel, but they are perpendicular. Lines EF and GH are not parallel as well.
To determine which segments or lines are parallel, we need to analyze their slope. The slope of a line is determined by the change in y over the change in x. Given that x = 15 and y = 60, we can use the equation of a line in slope-intercept form, y = mx + b, to determine their slopes.
If we have two lines with the same slope, then they are parallel. Let's consider the following segments and lines:
1. Segment AB with endpoints A(0, 15) and B(15, 15).
The slope of this segment is (15 - 15) / (15 - 0) = 0. Therefore, this segment is horizontal and its slope is 0.
2. Segment CD with endpoints C(0, 60) and D(15, 45).
The slope of this segment is (45 - 60) / (15 - 0) = -1.5.
3. Line EF with equation y = 2x - 30.
The slope of this line is 2.
4. Line GH with equation y = -0.5x + 67.5.
The slope of this line is -0.5.
Using the slope analysis, we can conclude that segments AB and CD are not parallel since their slopes are different. Line EF and GH are not parallel either because their slopes are different. However, segments AB and CD are perpendicular to each other since the product of their slopes is -1, which is the characteristic of perpendicular segments.
In summary, segments AB and CD are not parallel, but they are perpendicular. Lines EF and GH are not parallel as well.
To know more about segments visit :
https://brainly.com/question/31304314
#SPJ11
(9
Simplify. 5/4 • 6/25 + 6/5
Answers
Answer:
Exact Form:
3/2
Decimal Form:
1.5
Mixed Number Form:
1 1/2
Answer:
5/4*6/25+6/5=1.5
how is a good question
5/4=1.25
6/25=0.24
6/5=1.2
so...
1.25*0.24+1.2=1.5
Please solve this and show the steps on how you got your answer

Answers
well, let's take a look at the tickmarks on the triangle, the tickmarks mean that AC = CB, both AC and CB stemming out of vertex C, and both twin sides will make twin angles at the "base" or namely ∡A = ∡B, that means that 34 = x - 5, let's also recall that the sum of all interior angles in a triangle is 180°, so
\(34=x-5\implies \boxed{39=x} \\\\[-0.35em] ~\dotfill\\\\ \stackrel{\measuredangle A}{34}~~ + ~~\stackrel{\measuredangle B}{34}~~ + ~~\stackrel{\measuredangle C}{4y}~~ = ~~180\implies 68+4y=180 \\\\\\ 4y=112\implies y=\cfrac{112}{4}\implies \boxed{y=28}\)
Answer:
y = 28
Step-by-step explanation:
The dashes on line segments AC and BC indicate that the line segments are equal in length.
Therefore, as the triangle has two sides of equal length, it is an isosceles triangle.
The base angles of an isosceles triangle are equal, therefore ∠A = ∠B.
Interior angles of a triangle sum to 180°.
Therefore:
⇒ ∠A + ∠B + ∠C = 180°
⇒ 34° + 34° + 4y° = 180°
⇒ 68° + 4y° = 180°
⇒ 4y° = 112°
⇒ y = 112° ÷ 4°
⇒ y = 28
Help worth 100 points
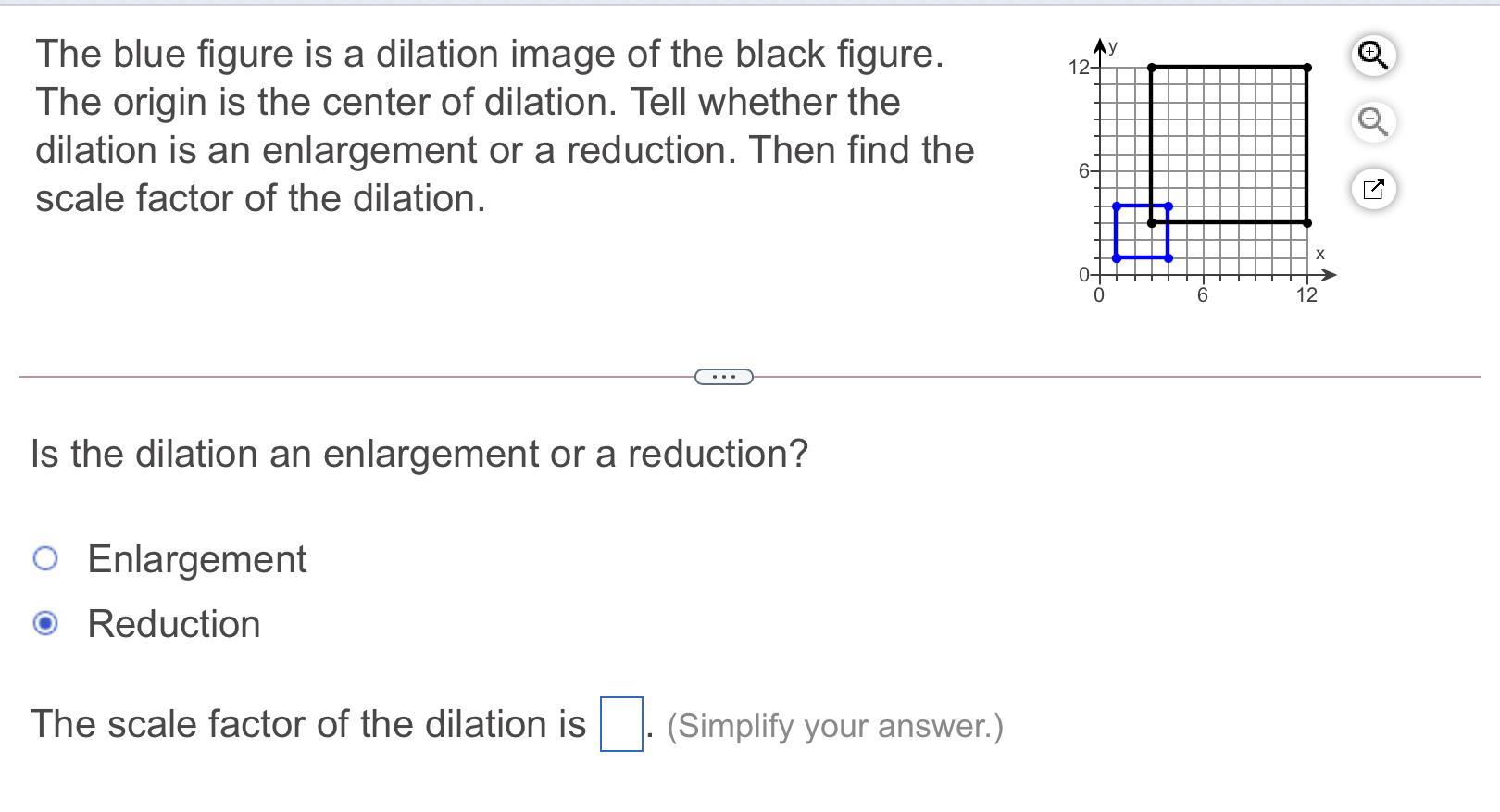
Answers
Answer:
It is a reduction because it is smaller than the original one.
The scale factor is 1/3 because the dimensions of the dilated figure is 3 by 3 units, which is 1/3 of the dimensions of the original figure; 9 by 9 units.
Answer:
Reduction
Step-by-step explanation:
As size is decreased it's reduction
Take two sides
Bigger=9unitsSmaller=3unitsscale factor :-
k=3/9k=1/3
Sarah got £72 for her birthday. She spent 40% of the money on
clothes and 1/6 of the remaining money on makeup. How much did she
have left over?
Answers
Solution: She has £36 remaining.
To solve this is fairly simple. First we multiple 72 by .4 to get 40%. This gives us 28.8.
We then subtract 28.8 by 72 to get the money she has remaining after she spends 40%. The answer to this is 43.2
Then she spends 1/6 on makeup. So we divide 43.2 by 6 and multiply again by 5, which gives us 36.
Find the solutions to x2 = 24.
=
O A. x = +4,16
=
O B.
X =
< = +2.1/6
O C. X= = +62
O D. x= 1514
=
Answers
Answer:
\(x\approx\pm4.8989\)
Step-by-step explanation:
\(x^2=24\)
\(\sqrt{x^2}=\sqrt{24}\)
\(x=\pm\sqrt{24}\)
\(x\approx\pm4.8989\)
Write it as in ascending order:
a)1:2, 3:5,3:10,3:2,4:5
Answers
Answer:
1) 3 : 10 (0.3)
2) 1 : 2 (0.5)
3) 3 : 5 (0.6)
4) 4 : 5 (0.8)
5) 3 : 2 (1.5)
Step-by-step explanation:
1 : 2 = 0.5
3 : 5 = 0.6
3 : 10 = 0.3
3 : 2 = 1.5
4 : 5 = 0.8
so
1) 3 : 10 (0.3)
2) 1 : 2 (0.5)
3) 3 : 5 (0.6)
4) 4 : 5 (0.8)
5) 3 : 2 (1.5)
Karen has $20 in an account that earns 10% interest compounded annually.
To the nearest cent, how much will she have in 2 years?
Answers
$24.20
Step-by-step explanation:Compound interest is the amount of interest paid on the principal and accumulated interest.
Interest Formula
The compound interest formula is \(A = P(1+\frac{r}{n} )^{nt}\). The variables for this formula are as follows:
A is the total amount in the accountP is the principal or the original balance of the account.r is the interest rate expressed as a decimaln is the number of times compounded per yeart is time in yearsTo find the total amount in Karen's account after 2 years, we need to define our variables and plug them into the formula.
Solving Compound Interest
Firstly, let's identify the value of each of the variables. The original amount in the account is $20. So, P = 20. Additionally, the interest rate is 10%, which is equal to 0.1. So, r = 0.1. Since interest is compounded annually, it is compounded once a year. Thus, n = 1. Finally, we want to know the amount after 2 years, so t = 2.
Now, let's plug these values into the formula above.
\(A=20(1+\frac{0.1}{1})^{1*2}\)This can be simplified to make the equation easier to solve.
A = 20(1.1)²Using this equation, we can say A = 24.20. Therefore, after 2 years, Karen will have $24.20 in her account.
1. Markov chains (a) Assume a box with a volume of 1 cubic metre containing 1 red particle (R) and 1 blue particle (B). These particles are freely moving in the box and we assume that they are perfectly mixed. We know that when they collide, blue and red particle stick to one another and form a compound particle RB. After a certain amount of time, RB decays again into one R and one B particle. R do not stick to R particles and B particles do not stick to B. After observing the system for a long time, we note that the RB particles remain together on average for 4 seconds before they decay. Equally, on average we wait for 1 second before particles R and B bind. Assume now that we have a box with 2 cubic metres volume and we seed the system with 3 R and 3 B particles. Interpret this system as a Markov chain assuming that particles of the same type are indistinguishable. Draw the transition diagram. In your answer, make sure that you make clear what each state means, and that you label the edges with the transition rates.
Answers
A Markov chain is a stochastic process in which the likelihood of an event happening is dependent solely on the outcome of the previous event. In a Markov chain, the future is independent of the past given the present.
Here, the Markov chain is described as a system that includes 1 red particle (R) and 1 blue particle (B) in a 1 cubic meter box.
When the R and B particles collide, they stick together and form a compound particle RB, which decays after a period of time into one R and one B particle.
The R particles do not adhere to other R particles, and the same is valid for B particles, which do not adhere to other B particles.
We observe that, on average, the RB particles stay together for 4 seconds before decaying, and the R and B particles stick together after waiting for 1 second.
We then consider a 2 cubic meter box containing 3 R and 3 B particles. This system can be interpreted as a Markov chain, with the states being the number of R and B particles.
The state is labeled by the number of red and blue particles present in the system at any given time, such as (2, 3) refers to the state with two red and three blue particles present in the box.
If we start with (3, 3), we can move to either (2, 3) or (3, 2) with equal probability.
The corresponding transition rate would be $3/2$ seconds per transition. After that, we could move to either (2, 2) or (1, 3) or (3, 1), with the corresponding transition rate being $3/4$ seconds per transition.
Finally, we could move to (2, 3) or (3, 2), with the corresponding transition rate being 4 seconds per transition. This is how the system can be interpreted as a Markov chain.
To know more about Markov chain, refer
https://brainly.com/question/25816915
#SPJ11
There are 20 different colored marbles in a bag and 4 of them are yellow. What
percentage of the marbles are yellow?

Answers
Answer:
20%
Step-by-step explanation:
4/20 * 100=20
a machine that is programmed to package 1.60 pounds of cereal is being tested for its accuracy in a sample of 40 cereal boxes, the sample mean filling weight is calculated as 1.62 pounds. the population standard deviation is known to be 0.06 pounds. find the 95% confidence interval for the mean.
Answers
The 95% confidence interval for the mean is (1.6048, 1.6352).Hence, option (d) is the correct answer.
As given, a machine that is programmed to package 1.60 pounds of cereal is being tested for its accuracy in a sample of 40 cereal boxes, the sample mean filling weight is calculated as 1.62 pounds. The population standard deviation is known to be 0.06 pounds. We are required to find the 95% confidence interval for the mean. Here are the steps to solve this problem:
The formula to find the confidence interval is as follows;
Lower limit = x - zα/2 (σ/√n)
Upper limit = x + zα/2 (σ/√n)
Where,
x= sample mean
zα/2 = z-value of the level of significance
σ = population standard deviation
n = sample size
We are given;
x = 1.62 pounds
σ = 0.06 pounds
n = 40
We need to find the z-value of the level of significance, which can be found using the z-table or by using the calculator.Using the z-table, we get the z-value at 95% confidence interval as zα/2 = 1.96
Substituting the values, we get
Lower limit = 1.62 - 1.96(0.06/√40)
Upper limit = 1.62 + 1.96(0.06/√40)
Lower limit = 1.6048, Upper limit = 1.6352
for more questions on confidence interval
https://brainly.com/question/20873848
#SPJ11
What is the slope of the line that passes through the points (-5, 8) and (-11, 8)?
Write your answer in simplest form.
Answers
Answer:
The slope is 0
Step-by-step explanation:
Using the slope formula \((y_{2}-y_{1})/(x_{2} - x_{2})\) you get:
8-8/ -11 - -5
0/-6
The slope is zero, a horizontal line through y = 8.
Answer:
m = 0
Step-by-step explanation:
Let P2 = (-11, 8)
P1 = (-5, 8)
Use the following equation for the slope:
\(m = \frac{(y \frac{}{2} - y \frac{}{1} )}{(x \frac{}{1} - x \frac{}{1} )} \)
= (8 - 8) / (-5 + 11)
= 0
This means that the line is horizontal.
No files!!! A expert or somebody pls help with me!!! Math.

Answers
Answer:
Number 3 is c)6.28cm
Number 4 is b)20.94
Number 5 is b)12.56m2
Find all the zeroes of polynomial 2x4
– 9x3 + 5x2 + 3x – 1 ,if two of its zeroes are 2 + √3 & 2 - √3
Answers
9514 1404 393
Answer:
x ∈ {-1/2, 1, 2-√3, 2+√3}
Step-by-step explanation:
The given zeros mean that one of the quadratic factors of the given polynomial is ...
(x -2)^ -3 = x^2 -4x +1
When that is factored out (see first attachment), the remaining quadratic is ...
2x^2 -x -1
This can be factored as ...
= (2x +1)(x -1)
which has roots that make these factors zero: x = -1/2, x = 1.
So, all of the zeros of the given polynomial are ...
-1/2, 1, 2-√3, 2+√3 . . . all zeros
__
A graphing calculator can often point to the zeros of the function quite nicely.
_____
Additional comments
When p is a zero of a polynomial, (x-p) is a factor of it. The given zeros mean that factors are (x-2-√3) and (x-2+√3). The product of these factors is the difference of the squares (x-2)^2 and (√3)^2, so is (x -2)^2 -3.
Using the pattern for the square of a binomial, we see this is ...
(x-2)^2 = x^2 -2·2x +2^2 = x^2 -4x +4
The product of the given factor is then 3 subtracted from this square. The given zeros mean there is a quadratic factor of ...
(x-2-√3)(x-2+√3) = (x-2)^2 -3 = x^2 -4x +4 -3 = x^2 -4x +1


The function f(r) gives the area of a circle with radius r.

Answers
Answer:
A. 50.24
Step-by-step explanation:
Put the value where the variable is and do the arithmetic.
f(4) = 3.14(4²) = 3.14×16 = 50.24
A camp director reviews the supply of string used for bracelet making. The graph shows the relationship between the number of yards of string used and the number of the bracelets made. What do the two points in the graph mean in terms of the situation?

Answers
Answer:
✅The point (4, 6) can be represented by the ratio, 4:6, and means 4 yards of strings made 6 bracelets.
✅The point (6, 9) can be represented by the ratio, 6:9, and means 6 yards of strings made 9 bracelets.
Step-by-step explanation:
The relationship between the number of yards of string used (x) and the number of the bracelets made (y) is a proportional relationship as shown by the given graph. The number of bracelets made is dependent on the number of strings used.
In terms of this situation, the two points on the graph mean the following:
✅The point (4, 6) can be represented by the ratio, 4:6, and means 4 yards of strings made 6 bracelets.
✅The point (6, 9) can be represented by the ratio, 6:9, and means 6 yards of strings made 9 bracelets.
Explain how to get the volume of this figure
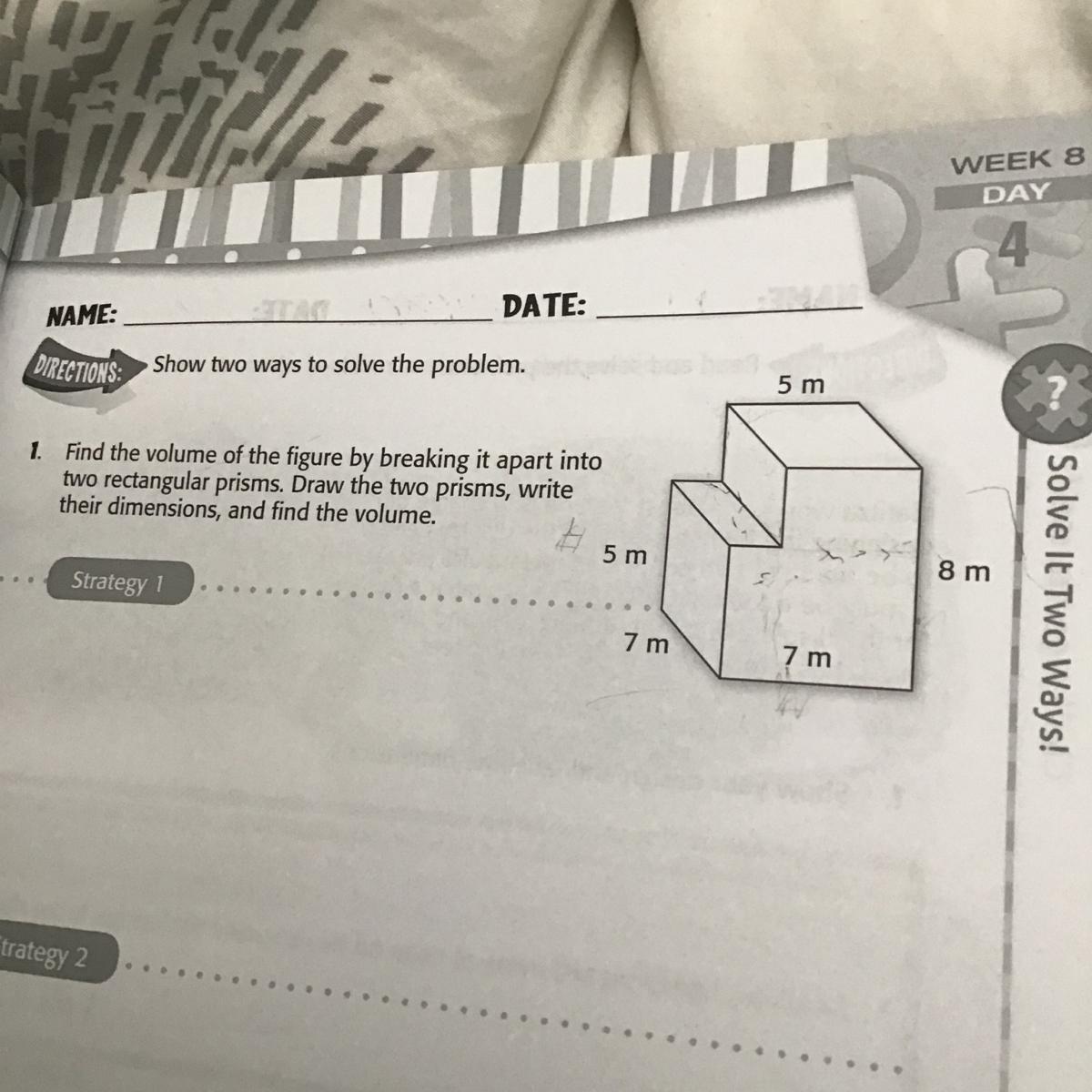
Answers
Answer:
350 meters cubed.
Step-by-step explanation:
If you visualize it, there are two rectangular prisms: one flat one on the top, and one large one on the bottom.
The width of the top one is 5 meters. The length is 7 meters. The height is 8 - 5 = 3 meters. So, one prism has a volume of 5m x 7m x 3m.
The width of the bottom one is 7 meters. The length is 7 meters. The height is 5 meters. So, the bottom prism has a volume of 7m x 7m x 5m.
(5 * 7 * 3) + (7 * 7 * 5)
= (35 * 3) + (49 * 5)
= 105 + 245
= 350
So, the volume of the figure is 350 meters cubed.
Hope this helps!
Translate this phrase into an algebraic expression.
The sum of 16 and twice a number
Use the variable n to represent the unknown number.
Answers
The answer is 2n + 16
what does 1/4(8x+16)=4x equal?
Answers
Answer:
x = 2
Step-by-step explanation:
Hope this helps, have a good day
pls help me with this question

Answers
Answer:
1. Wooden spoons
2. kitchen shears
3.cutting board
4. measuring spoons
5. measuring cups
6. Rubber spatulas
7. whisk
8. rotary beater
9. whisk
10. colander