WHAT IS A TAPE DIAGRAM AND WHAT DOES IT LOOK LIKE?
Answers
Answer:
A rectangular visual model resembling a piece of tape with divisions used to assist mathematical calculations. Also known as a divided bar model, fraction strip, length model or strip diagram. In mathematics education, it is used to solve word problems.
Step-by-step explanation:
Answer:
Tape diagrams are visual models that use rectangles to represent the parts of a ratio.
Here's what it looks like

Related Questions
There are 5 numbers, they are- 5,8,2,9,10
Find the mean, median and mode of it.
Answers
Answer:
Mean: 6.8
Median: 2
Mode: There's no mode
Step by step explanation:
Sum of all the numbers divided by 5The middle of the setNo mode in this setHope it helps ;)
Please mark as brainliest!
how to find the curve of intersection of two surfaces elliptic paraboloid
Answers
To find the curve of intersection of two surfaces, we need to set the equations of the two surfaces equal to each other and solve for the variables that describe the curve of intersection.
In this case, we will consider the intersection of two elliptic paraboloids. An elliptic paraboloid can be represented by the equation z = x^2/a^2 + y^2/b^2, where a and b are positive constants that determine the shape of the paraboloid.
To find the curve of intersection of two elliptic paraboloids, we set their equations equal to each other:
x^2/a^2 + y^2/b^2 = z = c^2/d^2 + w^2/e^2
where c, d, w, and e are also positive constants.
We can rearrange this equation to solve for one of the variables, say z:
z = x^2/a^2 + y^2/b^2 = c^2/d^2 + w^2/e^2
Now we can set z equal to a constant, say k:
k = x^2/a^2 + y^2/b^2
This equation represents the curve of intersection of the two elliptic paraboloids. To plot this curve, we can choose a range of values for x and y, and solve for the corresponding values of z. We can then plot these points in three-dimensional space to obtain the curve of intersection.
To learn more about curve of intersection click on,
https://brainly.com/question/4452427
#SPJ4
A ride at an amusement descends 24 feet each second. If the ride
lasts for 7 seconds, find the total change in elevation.
Answers
Answer: The ride descends 168 feet.
Step-by-step explanation:
24 Feet x 7 seconds = 168 feet
For every second it is 24 feet, so 24 x 7.
The total change in elevation will be descending 168 feet when the ride lasts for 7 seconds.
What is the Multiplication operation?In mathematics, Multiplication operations perform Multiplying values on either side of the operator.
For example 4×2 = 8
Given that a ride at an amusement descends 24 feet each second.
We have to determine the total change in elevation when the ride lasts for 7 seconds.
The total change in elevation is equal to the multiplication of 24 feet each second and the ride lasts for 7 seconds.
According to the given question, the solution would be
Total change in elevation = 24 Feet × 7 seconds
Apply the Multiplication operation,
Total change in elevation = 168 feet
Thus, the total change in elevation will be descending 168 feet when the ride lasts for 7 seconds.
Learn more about Multiplication operations here:
brainly.com/question/25834626
#SPJ2
f(x)=2x^4-8x^2+6
2 Differentiate 2 F(x) = 2x² - 8x² +6
Answers
To differentiate \(2F(x) = 2x^2 - 8x^2 + 6\), we need to find the derivative of each term separately. The derivative of \(2x^2\) is 4x, and the derivative of \(-8x^2\) is -16x.
To differentiate \(2F(x) = 2x^2 - 8x^2 + 6\), we can differentiate each term separately. The derivative of \(2x^2\) is found using the power rule, which states that the derivative of \(x^n\) is \(nx^{(n-1)}\). Applying this rule, the derivative of \(2x^2\) is 4x.
Similarly, the derivative of \(-8x^2\) is found using the power rule as well. The derivative of \(-8x^2\) is -16x.
Lastly, the derivative of the constant term 6 is zero since the derivative of a constant is always zero.
Combining the derivatives of each term, we have 4x - 16x + 0. Simplifying this expression gives us -12x.
Therefore, the derivative of \(2F(x) = 2x^2 - 8x^2 + 6\) is -12x.
Learn more about differentiation here:
https://brainly.com/question/24062595
#SPJ11
Using 6 bits in your answer, convert the base-10 value -21 to 2's complement binary.
2.Express the integer -4 in excess-16. Use 5 bits in your representation.
3.Using 6 bits in your answer, write the integer -26 using sign-magnitude binary representation.
4.The binary number shown here is a 6-bit excess-26 representation. What is its equivalent decimal (base 10) value?
101101
5.
A modified IEEE-754 floating-point representation uses 7 bits for the exponent and 10 bits for the fractional mantissa. The exponent is expressed in binary, excess-k. What is an appropriate value for k?
6. An IEEE-754 floating-point representation uses 3 bits for the fractional mantissa and 4 bits for the exponent (represented in excess-k). What is the largest positive value that can be represented? Express your answer in decimal (base 10).
Answers
1. To convert -21 to 2's complement binary using 6 bits:
- First, convert the absolute value of the number (21) to binary: 10101.
- Then, invert all the bits: 01010.
- Finally, add 1 to the inverted value: 01011.
So, the 6-bit 2's complement binary representation of -21 is 01011.
2. To represent -4 in excess-16 using 5 bits:
- Add the excess value (16) to the absolute value of the number (4): 20.
- Convert 20 to binary: 10100.
So, the 5-bit excess-16 representation of -4 is 10100.
3. To represent -26 in sign-magnitude using 6 bits:
- Convert the absolute value of the number (26) to binary: 11010.
- Set the leftmost bit as the sign bit (1 for negative).
- So, the 6-bit sign-magnitude representation of -26 is 111010.
4. To convert the 6-bit excess-26 binary number (101101) to decimal:
- Subtract the excess value (26) from the binary value: 101101 - 26 = 101075.
- The resulting decimal value is 75.
So, the decimal equivalent of the 6-bit excess-26 binary number 101101 is 75.
5. In IEEE-754 floating-point representation, the exponent is expressed in binary, excess-k. The value of k is determined by the number of bits used for the exponent. Since 7 bits are used for the exponent in this case, the value of k would be 2^(7-1) - 1 = 63. So, an appropriate value for k is 63.
6. In IEEE-754 floating-point representation, the largest positive value that can be represented depends on the number of bits used for the exponent and the fractional mantissa.
Since 3 bits are used for the fractional mantissa and 4 bits are used for the exponent in this case, the largest positive value that can be represented is determined by the maximum exponent value of 2^(4-1) - 1 = 7. Therefore, the largest positive value that can be represented is 2^7 = 128 in decimal (base 10).
To know more about binary refer here:
https://brainly.com/question/33333942#
#SPJ11
can someone help meee

Answers
Answer:
As radius=3
area=pie×r^2
=28.274
The vertical asymptote of the function = ln(x-6) + 5 is:
O A. x = -6
B. x = -5
O C. x = 6
D. x = 5
Answers
The vertical asymptote of the function = ln(x-6) + 5 is option C: x = 6.
The given function is f(x) = ln(x - 6) + 5.
A vertical asymptote is a vertical line that a function approaches but never crosses as it approaches infinity or negative infinity. For a logarithmic function like ln(x), the domain of the function is restricted to positive values only since the natural logarithm is undefined for non-positive arguments.
In the given function, we have f(x) = ln(x - 6) + 5. To find the vertical asymptote, we need to identify the value of x that would make the argument of the natural logarithm equal to zero.
Let's set the argument of the natural logarithm to zero:
x - 6 = 0
Now, solve for x:
x = 6
Thus, the value of x that would make the argument of the natural logarithm zero is x = 6.
So, the correct answer is option C: x = 6.
This means that the vertical asymptote of the function f(x) = ln(x - 6) + 5 is the vertical line x = 6. As x approaches 6 from either side (but never equaling 6), the function's values approach infinity. Similarly, as x approaches negative infinity, the function's values also approach infinity. The function never crosses the vertical line x = 6.
To know more about Function here
https://brainly.com/question/31056852
#SPJ2
a
Jaycee Alvarez deposits $300 in a savings account at City Bank. The account pays an annual interest rate of 5 percent. She makes no other
deposits or withdrawals. After three months the interest is calculated. How much simple interest does her money earn?
A А.
$3.95
С
$4.25
B
$4.00
D
$3.75
Answers
The answe is D. 3.75
hope this helps^^
The 7th grade class participated in the following
fitness challenges. If there are 250 students total,
how many participated in weight lifting?

Answers
Answer:
20 students
Step-by-step explanation:
Weight lifting:
8% = 0.08
250(0.08) = 20
what is the domain of f? khan academy

Answers
Answer:
x cannot = -2
Step-by-step explanation:
if x = -2 then the denominator is 0 and a fraction with 0 as a denominator is undefined.
Answer:
A
Step-by-step explanation:
f(x) = \(\frac{x-3}{x+2}\)
The denominator cannot be zero as this would make f(x) undefined.
Equating the denominator to zero and solving gives the value that x cannot be.
x + 2 = 0 ⇒ x = - 2 ← excluded value in the domain
The domain of f(x) is all real values of x such that x ≠ - 2
What is the complement of an angle of 41°?
(A) 41°
(B) 49°
(C) 139°
(D) 90°
(E) 180°
Answers
Convert 3.9m^2 into cm^2
I will leave good review!

Answers
Answer:
Step-by-step explanation:
To convert square meters to square centimeters, we need to multiply by the conversion factor (100 cm / 1 m)^2.
So,
3.9 m² = 3.9 × (100 cm / 1 m)²
3.9 m² = 3.9 × 10,000 cm²
3.9 m² = 39,000 cm²
Therefore, 3.9 square meters is equal to 39,000 square centimeters.
-17.R Using Percents, Homework
Sarted: Mar 10 at 8:30pm
Question 1 of 9
The Quick Slide Skate Shop sells the Ultra 2002 skateboard for a price of $60.20. However, the Quick Slide
Skate Shop is offering a one-day discount rate of 45% on all merchandise. About how much will the Ultra 2002
skateboard cost after the discount?
$33.00
$87.00
$46.20
$27.00
Answers
The price after discount is $33 and option 1 is the correct answer.
What is a discount?A discount is a drop in a product's or service's price. Discounts can be provided for a variety of purposes, such as to entice consumers to make larger purchases, to get rid of excess inventory, or to draw in new clients. Discounts can be represented as a set monetary amount or as a %, as in the example above. For instance, a shop may give customers $10 off any purchase of more than $50.
Given that, one-day discount rate of 45% is applied.
Thus,
Discount = 60.20 * 0.45 = 27.09
Price after discount = 60.20 - 27.09 = 33.11
Hence, the price after discount is $33 and option 1 is the correct answer.
Learn more about discount here:
https://brainly.com/question/16999193
#SPJ1
50 points!!!
7. Write and solve an inequality for the value of x.

Answers
The value of x must be between -18 and -6. The solution has been obtained using Triangle inequality theorem.
What is Triangle inequality theorem?
The triangle inequality theorem explains how a triangle's three sides interact with one another. This theorem states that the sum of the lengths of any triangle's two sides is always greater than the length of the triangle's third side. In other words, the shortest distance between any two different points is always a straight line, according to this theorem.
We are given three sides of a triangle as 8, 6 and x+20
Using Triangle inequality theorem,
⇒8+6 > x+20
⇒14 > x+20
⇒-6 > x
Also,
⇒x+20+6 > 8
⇒x+26 > 8
⇒x > -18
Also,
⇒x+20+8 > 6
⇒x+28 > 6
⇒x > -22
From the above explanation it can be concluded that x is less than -6 but greater than -22 and -18.
This means that x must lie between -18 and -6.
Hence, the value of x must be between -18 and -6.
Learn more about Triangle inequality theorem from the given link
https://brainly.com/question/1163433
#SPJ1
what is the y-intercept
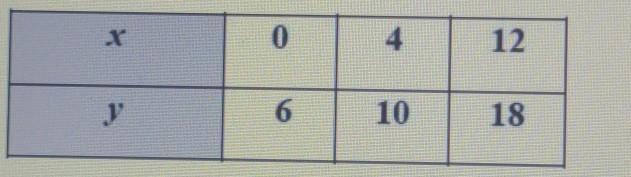
Answers
Answer:
(0,6)
Step-by-step explanation:
The y intercept is where the line crosses the y axis or the coordinate where x = 0.
Here, when x is equal to 0, y is equal to 6 meaning that the y intercept is at (0,6)
Neal estimated √50 by determining that the two perfect squares nearest 50 are 49 and 64. select the two consecutive whole numbers that the √50 is between to complete the sentence. √50 is between and .
Answers
Two consecutive whole numbers representing the estimated square root of 50 are 7 and 8.
Number need to estimate square root = 50
To estimate √50,
Neal found that the two perfect squares nearest 50 are 49 and 64.
Since 50 is closer to 49 than to 64,
Square root of 49 is equal to 7
Square root of 64 is equal to 8.
We know that √50 is closer to the square root of 49 which is 7.
Estimated two consecutive whole numbers are 7 and 8.
Therefore, estimated √50 is between the two consecutive whole numbers 7 and 8.
Learn more about estimation here
brainly.com/question/11679843
#SPJ4
The above question is incomplete, the complete question is:
Neal estimated √50 by determining that the two perfect squares nearest 50 are 49 and 64. Select the two consecutive whole numbers that the √50 is between to complete the sentence.
i know this is a simple question but i am confused hah, can someone help me

Answers
Answer:
469.875 square feet
Step-by-step explanation:
All you have to do for this question is multiply 3.75 bags of soil * 125.3 feet per bag.
\(3.75 * 125.3 = 469.875\) square feet

Fill in the blanks. the vector x = c1 −1 1 e−9t c2 5 3 e7t is a solution of the initial-value problem x' = 1 10 6 −3 x, x(0) = 2 0
Answers
The vector x = [c1 - e^-9t, c2 + 3e^7t, c1 + 5e^7t] is a solution of the initial-value problem x' = [1/10, 6, -3]x, x(0) = [2, 0, 1].
To verify that the given vector x is a solution to the initial-value problem, we need to take its derivative and substitute it into the differential equation, and then check that it satisfies the initial condition.
Taking the derivative of x, we have:
x' = c1(-1/10)e^(-9t) + c2(35)e^(7t) -1/10
5c2e^(7t)
Substituting x and x' into the differential equation, we have:
x' = Ax
x' = [ 1 10 6 −3 ] [ c1 −1 1 e−9t c2 5 3 e7t ] = [ (−1/10)c1 + 5c2e^(7t) , c1/10 − c2e^(7t) , 6c1e^(-9t) + 3c2e^(7t) ]
So, we need to verify that the following holds:
x' = Ax
That is, we need to check that:
(−1/10)c1 + 5c2e^(7t) = c1/10 − c2e^(7t) = 6c1e^(-9t) + 3c2e^(7t)
To check that the above equation holds, we first observe that the first two entries are equal to each other. Therefore, we only need to check that the first and third entries are equal to each other, and that the initial condition x(0) = [c1, 0] is satisfied.
Setting the first and third entries equal to each other, we have:
(−1/10)c1 + 5c2e^(7t) = 6c1e^(-9t) + 3c2e^(7t)
Multiplying both sides by 10, we get:
-c1 + 50c2e^(7t) = 60c1e^(-9t) + 30c2e^(7t)
Adding c1 to both sides, we get:
50c2e^(7t) = (60c1 + c1)e^(-9t) + 30c2e^(7t)
Dividing both sides by e^(7t), we get:
50c2 = (60c1 + c1)e^(-16t) + 30c2
Simplifying, we get:
50c2 - 30c2 = (60c1 + c1)e^(-16t)
20c2 = 61c1e^(-16t)
This equation must hold for all t. Since e^(-16t) is never zero, we must have:
20c2 = 61c1
Therefore, c2 = (61/20)c1. Substituting this into the initial condition, we have:
x(0) = [c1, 0] = [2, 0]
Solving for c1 and c2, we get:
c1 = 7/2 and c2 = -3/2
Thus, the solution to the initial-value problem is:
x(t) = [ (7/2) −1 1 e^(-9t) (−3/2) 5 3 e^(7t) ]
and we can verify that it satisfies the differential equation and the initial condition.
To know more about vector,
https://brainly.com/question/31737683
#SPJ11
You perform a Chi-Square test and obtain a p-value lower than 0.01. What does that mean?
Answers
Performing a Chi-Square test is a statistical tool used to determine if there is a significant difference between observed and expected data. The test helps to analyze categorical data by comparing observed frequencies to the expected frequencies. The p-value in a Chi-Square test refers to the probability of obtaining the observed results by chance alone.
If a p-value lower than 0.01 is obtained in a Chi-Square test, it means that the results are statistically significant. In other words, there is strong evidence to reject the null hypothesis, which states that there is no significant difference between the observed and expected data. This means that the observed data is not due to chance alone, but rather to some other factor or factors.
The mean, or average, is not directly related to the Chi-Square test or the p-value. The Chi-Square test is specifically used to determine the significance of the observed data. However, the mean can be used as a measure of central tendency for continuous data, but it is not applicable to categorical data.
In conclusion, obtaining a p-value lower than 0.01 in a Chi-Square test means that there is strong evidence to reject the null hypothesis, and that the observed data is statistically significant.
learn more about Chi-Square here: brainly.com/question/24976455
#SPJ11
5. Twenty students in Mr. Martin's class each took a survey about the number of minutes they played outside. The box
plots represent the amount of time the students spent outside playing in the summer and in the winter. Which statement is
best supported by the data?
SUMMER WINTER
30
45
60
NUMBER OF MINUTES
75
90
A. The range of number of minutes outside is the same in the
summer and in the winter.
B. The median number of minutes outside in the summer is
equal to the maximum number of minutes outside in
the winter.
C. The interquartile range for the number of minutes outside is
the same in the summer and in the winter.
D. The minimum number of minutes outside in the summer is
the same as the first quartile in the winter.
Answers
The statement "The median number of minutes outside in the summer is equal to the maximum number of minutes outside in the winter" is best supported by the data (option B).
How to find the maximum number of minutes outside?Looking at the plot;
Winter: Minimum= 0 Maximum= 60 Median= 30
Range = 60 - 0 = 60
Summer: Minimum= 20 Maximum= 90 Median= 60
Range = 90 - 20 = 70
So the median number of minutes outside in the summer is
equal to the maximum number of minutes outside in the winter.
Learn about Mean and Median here https://brainly.com/question/26177250
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached image.

a score of x = 70 on an exam with µ = 82 and σ = 8, or a score of x = 60 on an exam with µ = 72 and σ = 12?
Answers
A score of x = 60 on an exam with μ = 72 and σ = 12 is comparatively better than a score of x = 70 on an exam with μ = 82 and σ = 8.
To compare the two scores, we can convert them to z-scores, which tell us how many standard deviations a particular value is from the mean. The formula for z-score is:
z = (x - μ) / σ
where x is the value, μ is the mean, and σ is the standard deviation.
For the first score of x = 70 on an exam with μ = 82 and σ = 8, the z-score is:
z = (70 - 82) / 8 = -1.5
For the second score of x = 60 on an exam with μ = 72 and σ = 12, the z-score is:
z = (60 - 72) / 12 = -1.0
The z-score for the first score is lower than the z-score for the second score, which means that the first score is further below its mean than the second score is below its mean. Therefore, we can say that a score of x = 60 on an exam with μ = 72 and σ = 12 is comparatively better than a score of x = 70 on an exam with μ = 82 and σ = 8.
For more questions on Z-Score
https://brainly.com/question/28000192
#SPJ4
A landscaper buried a water line around a rectangular lawn to serve as a supply line for a sprinkler system. The length of the lawn is 6 times its width. If 630 feet of pipe was used to do the job, what is the length and the width of the lawn
Answers
Answers:
Length = 270 feet
Width = 45 feet
========================================================
Work Shown:
x = width
6x = length, since it is 6 times the width
P = perimeter of rectangle
P = 2*(Length + Width)
P = 2*(6x + x)
P = 2*(7x)
P = 14x
Plug in the given perimeter P = 630 and solve for x.
P = 14x
14x = P
14x = 630
x = 630/14
x = 45
The width is 45 feet.
The length must be 6x = 6*45 = 270 feet.
The required length and width of the lawn is given as Length = 270 feet and Width = 45 feet.
Given that,
A landscaper buried a water line around a rectangular lawn to serve as a supply line for a sprinkler system. The length of the lawn is 6 times its width. If 630 feet of pipe was used to do the job, what is the length and the width of the lawn is to be determined.
Perimeter is the measure of the figure on its circumference.
Here,
let the length be l and the width be w,
According to the question,
l = 6w
and
Perimeter of the lawn = 630
2 [l + w] = 630
2 [6w + w] = 630
14w = 630
w = 45
Now,
l = 45[6] = 270
Thus, the required length and width of the lawn is given as Length = 270 feet and Width = 45 feet.
learn more about perimeter here:
brainly.com/question/6465134
#SPJ2
1. Which function is quadratic?
A 3x – 2y = 5
B 5x2 + x = y - 4
Answers
Because the formula of quadratic equations is y = ax² + bx + c where you can see the only equation with the power of two is equation B
Equation B into quadratic equation
5x² + x = y - 4
y = 5x² + x +4
Function 5x² + x = y - 4 is quadratic .
Hence option B is correct .
Given , Linear and Quadratic function.
Standard form of quadratic function : y = ax² + bx +c
a = coefficient of x² .
b = coefficient of x .
c = constant .
Rearranging the function,
5x² + x = y - 4
y = 5x² + x - 4
Comparing the equation with standard form,
a = 5
b = 1
c = -4
Hence option B is correct .
Know more about quadratic equation,
https://brainly.com/question/15952797
#SPJ6
What is m∠ abd? justify using geometry vocabulary.
Answers
In the given figure, the measure of angle ABD is 120 degrees
From the given figure
The measure of angle CBD = 60 degrees
We know the sum of angles on a straight line add up to 180 degrees.
Here the line AC is straight line
Therefore, the sum of the measure of angle ABD and measure of angle CBD is equal to 180 degrees, so the angle ABD and angle CBD are supplementary angles
Angle ABD + Angle CBD = 180 degree
Substitute the values in the equation
∠ABD + 60 = 180
∠ABD = 180 - 60
∠ABD = 120 degree
Therefore, the angle ABD is 120 degrees
Learn more about supplementary angle here
brainly.com/question/13045673
#SPJ4

Look at the graph, how many factors would it have?

Answers
Here is some info that might help
-2 factors is a hint
+0 +2 +4 is a fractor of 4/1
if not 41

find the surface area of the prism to the nearest tenth.

Answers
To determine the surface area of the prism we need add the following areas:
• Two triangles with base of 6 in and height 4 in.
,• Two rectangles with length 10 in and width 5 in
,• One rectangle with length 10 in and width 6 in.
Then the surface area is:
\(\begin{gathered} SA=2(\frac{1}{2}\cdot6\cdot4)+2(10\cdot5)+10\cdot6 \\ SA=24+100+60 \\ SA=184 \end{gathered}\)Therefore, the surface area is 184 square inches
Use the graph to evaluate the limits. lim f(x) and lim f(x) X→-1+ x→-1 -3 -2 2- 1- -N 2 O A. -7; -5 OB. -7; -2 O C. -2; -7 O D. -5; -2
Answers
The correct option is (OB) -7; -2.
By analyzing the graph, it is observed that as x approaches -1 from the right side (i.e., x → -1+), lim f(x) = -7. And as x approaches -1 from the left side (i.e., x → -1-), lim f(x) = -2.
Limits are values that a function approaches as the input value gets closer to a certain point. The limit can be either a real number or infinity. The limit of a function is defined in a variety of ways, but a common approach is to define it as the value that the function approaches as the input approaches a certain point. The left and right limits of a function are computed using a similar method, except the input approaches the point from either the left or right side, respectively.
The graph of a function f(x) is shown in the figure, and we have to evaluate the limits of the function as x approaches -1. The limits of a function are the values that the function approaches as the input value approaches a particular point. It can either be a real number or an infinity. The given function has a jump discontinuity at x = -1. At x = -1, the left-hand limit and the right-hand limit do not exist, but the overall limit does exist, which is a finite number. As x approaches -1 from the right side (i.e., x → -1+), the value of the function approaches -7. And as x approaches -1 from the left side (i.e., x → -1-), the value of the function approaches -2. Therefore, we can conclude that the limits of the given function as x approaches -1+ and x approaches -1- are -7 and -2, respectively. In summary,lim f(x) = -7 and lim f(x) = -2 as x approaches -1+ and x approaches -1-, respectively. Hence, the correct option is (OB) -7; -2.
To know more about discontinuity visit
brainly.com/question/28914808
#SPJ11
please help me thank you :)

Answers
Answer:
use google
Step-by-step explanation:
what is 6.3 x 10 to the negative eighth power in standard form
Answers
Answer:
6.3e-8
Step-by-step explanation:
Hoped this helped :)
how are you supposed to multiply fraction?