What is a slope? how do figure it out?
Answers
Slope:
Slope is define as steepness of the line and commonly know as rise over run . it defineas ratio of change in y with respect to x.
To figur out the slope :
\(m=\frac{\Delta y}{\Delta x}\)\(\begin{gathered} \Delta y=y_2-y_1 \\ \Delta x=x_2-x_1 \end{gathered}\)slope is:
\(\begin{gathered} m=\frac{y_2-y_1}{x_2-x_1} \\ \end{gathered}\)\(\begin{gathered} (x_1,y_1) \\ (x_2,y_2) \end{gathered}\)Are point that is exist this line.
Related Questions
What are mZR and m2S? S T T R 1000 940 9 mZR mZS = o
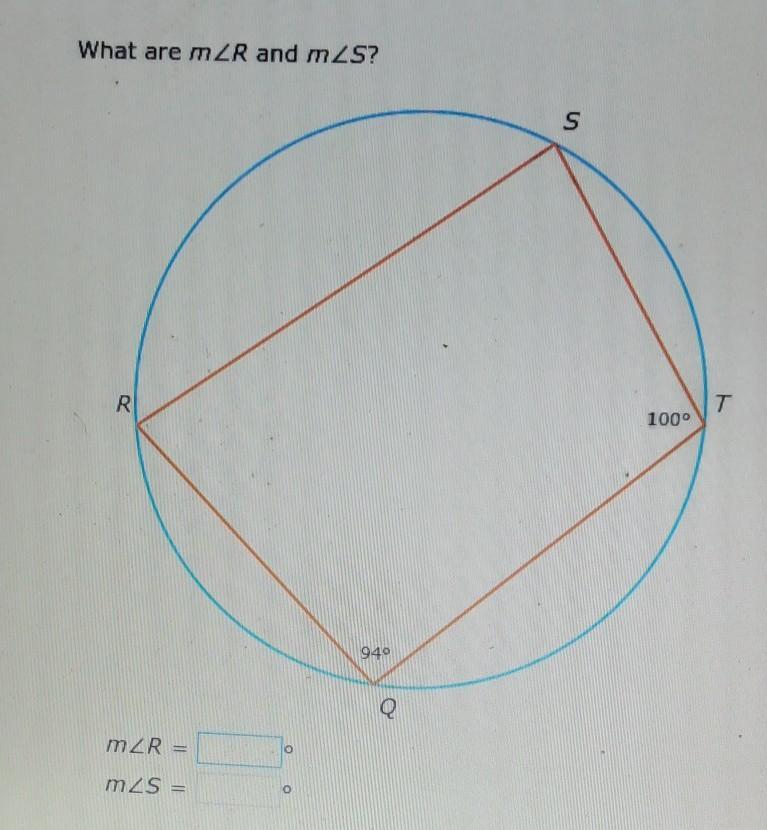
Answers
The measure of the angles R and S are 80° and 86° respectively.
A 4-sided polygon with four inner angles totaling 360 degrees is referred to as a quadrilateral.
A circle is a rounded shape whose edge is made up of a series of points that are all the same distance from the circle's center. The radius of the circle is this predetermined distance.
Quadrilateral QRST is inscribed in a circle.
The opposite angles of the quadrilateral inscribed in a circle are supplementary to each other.
Therefore,
m∠T + m∠R = 180°
100° + m∠R = 180°
Subtracting 100° from each side of the equation,
100° + m∠R - 100° = 180° - 100°
m∠R = 80°
Similarly,
m∠Q + m∠S = 180°
94° + m∠S = 180°
Subtracting 94° from each side of the equation,
94° + m∠S - 94° = 180° - 94°
m∠S = 86°
Learn more about angles here:
brainly.com/question/25770607
#SPJ9
PLEASE HELP PLEASEEEEE
Part A: Explain why the x-coordinates of the points where the graphs of the equations y = 5−x and y = 2x + 1 intersect are the solutions of the equation 5−x = 2x + 1.
Part B: Make tables to find the solution to 5−x = 2x + 1. Take the integer values of x between −3 and 3.
Part C: How can you solve the equation 5−x = 2x + 1 grap hically?
Answers
Answer:
y = 5 - x → standard form y = -x + 5
y = 2x + 1
A: If two sides of an equation are set equal to each other, their value is a point of intersection because they will both equal a certain value.
B:
3 → 5 - 3 = 2(3) + 1 → 2 = 6 + 1 → 2 ≠ 7
2 → 5 - 2 = 2(2) + 1 → 3 = 4 + 1 → 3 ≠ 5
1 → 5 - 1 = 2(1) + 1 → 4 = 2 + 1 → 4 ≠ 3
0 → 5 - 0 = 2(0) + 1 → 5 = 0 + 1 → 5 ≠ 1
-1 → 5 - (-1) = 2(-1) + 1 → 6 = -2 + 1 → 6 ≠ -1
-2 → 5 - (-2) = 2(-2) + 1 → 7 = -4 + 1 → 7 ≠ -3
-3 → 5 - (-3) = 2(-3) + 1 → 8 = -6 + 1 → 8 ≠ -5
algebraically ↓
-x + 5 = 2x + 1 → 4 = 3x → x = 4/3
C: graphically
graph both equations and find point of intersection
We know these points are the solutions to \(5-x=2x+1\) because by setting the two equations equal to each other, we find where they intersect, and those points are the solutions to the equation.
Part B\(\begin{array}{|c|c|c|c|}\cline{1-4}\bf x&\bf5-x&\bf2x+1&\bf5-x=2x+1\\\cline{1-4}-3&8&-5&8\neq-5\\\cline{1-4}-2&7&-3&7\neq-3\\\cline{1-4}-1&6&-1&6\neq-1\\\cline{1-4}0&5&1&0\neq1\\\cline{1-4}1&4&3&4\neq3\\\cline{1-4}2&3&5&3\neq5\\\cline{1-4}3&2&7&2\neq7\\\cline{1-4}\end{array}\)
Part B and a halfSince none of those values are correct solutions, let's solve this equation algebraically, even though the question doesn't ask for us to do so.
\(\begin{aligned}5-x&=2x+1\\-x&=2x+1-5\\-x-2x&=1-5\\-3x&=-4\\x&=\boxed{\frac{4}{3}}\end{aligned}\)
Part CWe can solve the equation graphically by graphing both \(y=5-x\) and \(y=2x+1\), then finding where they meet. This is shown in the attachment below.

Can someone give me the correct answers for this with explanation on what I did wrong and how to fix it (first part)
Don’t worry about question 6

Answers
write the decimalas a percent 4.68
Answers
Answer:
468% is the percent of 4.68
Step-by-step explanation:
4.68 x 100 = 468
A nine-month old baby drank an average of 7 1/4 oz during each of four feedings. If the baby drank 7 1/2oz, 7 3/8oz, & 6 3/8oz in the first three feedings, how many ounces were taken during the fourth feeding?
A) 7 3/8
B) 6 3/8
C) 6 3/4
D) 7 3/4
Show work please
Answers
Answer: D) 7 3/4
Step-by-step explanation:
With averages, we add all the values and divide by the number of values. Here, we know three out of the four days, let's label the day we don't know x. There are four days, so we can divide by four. 7 1/4 is the average, so we can set the equation equal to 7 1/4.
7 1/4 = (7 1/2 + 7 3/8 + 6 3/8 + x) / 4
Let's multiply both sides by 4 to get rid of the fraction. Let's also add what is in the parentheses
29 = 21 1/4 + x
Now we can isolate x by subtracting 29-21 1/4
so
x = 7 3/4 thus the answer is D
Answer:
D) 7 3/4
Step-by-step explanation:
Let x = amount of last feeding.
7 1/4 = (7 1/2 + 7 3/8 + 6 3/8 + x)/4
4 × 7 1/4 = 7 1/2 + 7 3/8 + 6 3/8 + x
28 + 1 = 7 4/8 + 7 3/8 + 6 3/8 + x
29 = 20 10/8 + x
(20 10/8 is the same as 20 + 10/8 = 20 + 8/8 + 2/8 = 20 + 1 + 1/4 = 21 + 1/4 = 21 1/4)
29 = 21 2/8 + x
29 = 21 1/4 + x
x = 29 - 21 1/4
x = 28 4/4 - 21 1/4
x = 7 3/4
Answer: 7 3/4
If x varies directly as y, find x when y = 8 a) x = 6 when y = 32 b) x = 14 when y = -2
Answers
a) The value of x is 42.6 when k =16/3 is directly proportional to y.
b) The value of x is -56 when k is -7 is directly proportional to y.
What kind of variation is one where x and y are directly proportional?
If x = ky for some constant k can be used to indicate the relationship between the variables y and x, then we may say that y varies directly with y or that x is directly proportional to y.x varies directly as y
x α y
x = ky
a) x=6 ; y = 32
x = ky
6 = k(32)
k = 16/3
if y = 8
then,
x = (16/3) * 8
= 128/3
x = 42.6
Hence, the value of x is 42.6 when k =16/3 is directly proportional to y.
b) x= 14 and y = -2
x = ky
14 = k(-2)
k = -7
if y = 8
then,
x = ky
x= (-7) 8
x = -56
Hence, the value of x is -56 when k is -7 is directly proportional to y.
To know more about proportional check the below link:
https://brainly.com/question/870035
#SPJ1
solve pls brainliest

Answers
In coordinates, the first number is the x and the second one is y. In (4,2), 4 is the x and 2 is the y. The x axis goes from left to right and the y axis goes from up to down.

JKLM is a rhombus.
m/JMN = (-x+69)*
mZLMJ = (-6x +166)
K
N
M
Find the mZLKN.
label optional

Answers
The angle LKN in the rhombus is 62 degrees.
How to find angles in a rhombus?A rhombus is a quadrilateral that has 4 sides equal to each other. The sum of angles in a rhombus is 360 degrees.
Opposite angles are equal in a rhombus. The diagonals bisect each other at 90 degrees. Adjacent angles add up to 180 degrees.
Therefore, let's find ∠LKN as follows:
m∠JMN = (-x + 69)
m∠LMJ = (-6x + 166)
Therefore,
1 / 2 (-6x + 166) = -x + 69
-3x + 83 = -x + 69
-3x + x = 69 - 83
-2x = -14
x = -14 / -2
x = 7
Therefore,
∠LKN = 1 / 2 (-6x + 166)
∠LKN = 1 / 2 (-6(7) + 166)
∠LKN = 1 / 2 (-42 + 166)
∠LKN = 62 degrees
learn more on rhombus here: https://brainly.com/question/30995617
#SPJ1
write the number 16, 107, 320 in expanded
form.
Answers
398383i4irujidifififif
Picture included!
Find the unknowns in the graph below:

Answers
All the values of x, y and z are,
z = 12.99
y = 7.01
x = 28.3 degree
We have to given that;
In a triangle,
Two angles are, 61.7 degree and 90 degree
And, One side is, 14.76.
Now, We can formulate;
sin 61.7° = Perpendicular / Hypotenuse
sin 61.7° = z / 14.76
0.88 = z / 14.76
z = 0.88 x 14.76
z = 12.99
And, By Pythagoras theorem we get;
14.76² = z² + y²
14.76² = 12.99² + y²
217.85 = 168.74 + y²
y² = 217.85 - 168.74
y² = 49.1
y = 7.01
And, By sum of all the angles in triangle, we get;
x + 61.7 + 90 = 180
x + 151.7 = 180
x = 180 - 151.7
x = 28.3 degree
Learn more about the triangle visit;
brainly.com/question/1058720
#SPJ1
Find the solution for a 2x2 matrix A:
[4 4
0 1] to the nth power = [ ]
Answers
Answer:
Step-by-step explanation:
Answer:
A^n = [4^n 4^n
0 1]
Step-by-step explanation:
To find the solution for the 2x2 matrix A:
[4 4
0 1] to the nth power = [ ]
We can use matrix multiplication to raise A to the nth power. Let's start with n = 1:
A^1 = [4 4
0 1]
Now, let's solve for A^2 by multiplying A^1 by A:
A^2 = A x A^1
= [4 4 [4 4
0 1] 0 1]
= [16 16
0 1]
Next, let's solve for A^3:
A^3 = A x A^2
= [4 4 [16 16
0 1] 0 1]
= [64 64
0 1]
We can see a pattern emerging:
A^1 = [4 4
0 1]
A^2 = [16 16
0 1]
A^3 = [64 64
0 1]
We can generalize this pattern as follows:
A^n = [4^n 4^n
0 1]
Therefore, the solution for the 2x2 matrix A raised to the nth power is:
A^n = [4^n 4^n
0 1]
Can someone help please
ASAP

Answers
Answer:
see explanation
Step-by-step explanation:
using the tangent ratio in the right triangle
tan A = \(\frac{opposite}{adjacent}\) = \(\frac{BC}{AB}\) = \(\frac{5}{11}\) , then
∠ A = \(tan^{-1}\) ( \(\frac{5}{11}\) ) ≈ 24.4° ( to 1 decimal place )
tan C = \(\frac{opposite}{adjacent}\) = \(\frac{AB}{BC}\) = \(\frac{11}{5}\) , then
∠ C = \(tan^{-1}\) ( \(\frac{11}{5}\) ) ≈ 65.6° ( to 1 decimal place )
using Pythagoras' identity in the right triangle
the square on the hypotenuse is equal to the sum of the squares on the other two sides, that is
AC² = AB² + BC² = 11² + 5² = 121 + 25 = 146 ( take square root of both sides )
AC = \(\sqrt{146}\) ≈ 12.08 ( to 2 decimal places )
Felix is constructing a three-dimensional figure. First he draws the views for the figure. A bottom row of 6 cubes, second row of 3 cubes, and top row of 3 cubes. A column of 2 cubes. A bottom row of 6 cubes, and second row of 2 cubes. Column of 3 cubes. Which views can Felix use to construct the same figure? A bottom row of 6 cubes, second row of 3 cubes, and top row of 1 cube. A bottom row of 6 cubes and second row of 2 cubes. A bottom row of 6 cubes, second row of 3 cubes, and top row of 1 cube. A bottom row of 6 cubes and second row of 2 cubes. A bottom row of 6 cubes, second row of 3 cubes, and top row of 1 cube. A column of 2 cubes. A column of 3 cubes. A bottom row of 6 cubes and second row of 2 cubes. A column of 2 cubes. A column of 3 cubes.
Answers
A view which Felix can use to construct the same figure include the following: A. a bottom row of 6 cubes, second row of 3 cubes, and top row of 1 cube.
What is an isometric sketch?In Mathematics and Geometry, an isometric sketch is sometimes referred to as an isometric drawing and it can be defined as a graphical (pictorial) representation of a physical object or geometric shape in technical and engineering drawings, especially by drawing all its three dimensions (3D) at full scale;
Front viewEnd viewPlanIn this context, we can reasonably infer and logically deduce that the front view is a view which Felix can use to construct the same three-dimensional figure because its orientation influences the other views.
Read more on front view and dimensions here: https://brainly.com/question/29242295
#SPJ1

A construction company will be penalized each day of delay in construction for bridge. The penalty will be $4000 for the first day and will increase by $10000 for each following day. Based on its budget, the company can afford to pay a maximum of $ 165000 toward penalty. Find the maximum number of days by which the completion of work can be delayed.
Answers
Answer:
The answer toy our problem is, The maximum number of days by which the completion of work can be delayed is 15.
Step-by-step explanation:
We are given that the penalty amount paid by the construction company from the first day as sequence, 4000, 5000, 6000, ‘ and so on ‘. The company can pay 165000 as penalty for this delay at maximum that is
\(S_{n}\) = 165000.
Let us find the amount as arithmetic series as follows:
4000 + 5000 + 6000
The arithmetic series being, first term is \(a_{1}\) = 4000, second term is \(a_{2}\) = 5000.
We would have to find our common difference ‘ d ‘ by subtracting the first term from the second term as shown below:
\(d = a_{2} - a_{1} = 5000 - 4000 = 1000\)
The sum of the arithmetic series with our first term ‘ a ‘ which the common difference being, \(S_{n} = \frac{n}{2} [ 2a + ( n - 1 )d ]\) ( ‘ d ‘ being the difference. )
Next we can substitute a = 4000, d = 1000 and \(S_{n}\) = 165000 in “ \(S_{n} = \frac{n}{2} [ 2a + ( n - 1 )d ]\) “ which can be represented as:
Determining, \(S_{n} = \frac{n}{2} [ 2a + ( n - 1 )d ]\)
⇒ 165000 = \(\frac{n}{2}\) [( 2 x 4000 ) + ( n - 1 ) 1000 ]
⇒ 2 x 165000 = n(8000 + 1000n - 1000 )
⇒ 330000 = n(7000 + 1000n)
⇒ 330000 = 7000n + \(1000n^2\)
⇒ \(1000n^2\) + 7000n - 330000 = 0
⇒ \(1000n^2\) ( \(n^2\) + 7n - 330 ) = 0
⇒ \(n^2\) + 7n - 330 = 0
⇒ \(n^2\) + 22n - 15n - 330 = 0
⇒ n( n + 22 ) - 15 ( n + 22 ) = 0
⇒ ( n + 22 )( n - 15 ) = 0
⇒ n = -22, n = 15
We need to ‘ forget ‘ the negative value of ‘ n ‘ which will represent number of days delayed, therefore, we get n=15.
Thus the answer to your problem is, The maximum number of days by which the completion of work can be delayed is 15.
If the median is 3.5, we can assume the mean is ____________than 3.5
Answers
We cannot make a general assumption about whether the mean is greater or less than 3.5 based solely on the fact that the median is 3.5.
What is mean?The mean is a measure of central tendency that represents the average value of a set of numbers. It is also called the arithmetic mean or simply the average.
According to question:We cannot make a general assumption about whether the mean is greater or less than 3.5 based solely on the fact that the median is 3.5.
The mean and the median are two different measures of central tendency, and they can have different values depending on the distribution of the data. In general, if a data set is symmetric and bell-shaped, the mean and the median are close to each other. However, if the data set is skewed, the mean and the median may be different.
For example, consider the following two data sets:
Set 1 data: 1, 2, 3, 4, and 5.
The median is 3.
The mean is (1 + 2 + 3 + 4 + 5) / 5 = 15 / 5 = 3.
Data set 2: 1, 2, 3, 4, 10
The median is 3.
The mean is (1 + 2 + 3 + 4 + 10) / 5 = 20 / 5 = 4.
In data set 1, the mean is the same as the median. In data set 2, the mean is greater than the median because the value 10 is an outlier that pulls the mean up.
Therefore, without additional information about the distribution of the data, we cannot make a general assumption about whether the mean is greater or less than 3.5 based solely on the fact that the median is 3.5.
To know more about mean visit:
https://brainly.com/question/10853033
#SPJ1
Which two expressions are equivalent?

Answers
Answer:
option 3
Step-by-step explanation:
12 - (y*2) = 12 - (2*y) Commutative property
2*y = y*2
Otto had two days to paint 9 paintings. He painted 5 1\5 yesterday. How many paintings does Otto need to paint today?
Answers
Answer:
He needs to paint 3 4/5 today.
Step-by-step explanation:
9 - 5 1/5 = 3 4/5
Otto will need to paint 3 4/5 today.
Answer:
3 1/2
If he
1/2 + 1/2 equals one .
Therefore, it being he needs to finish
write the equation of th eline that is parallel to x=8 and that passes through the point (-3,-2)
Answers
In order to find the parallel line, it has to have the same slope. Different b value (mx+b, but the m has to be the same).
Since the question is asking for a parallel line, you know that it also has to be vertical, to keep it consistent.
Since it is asking for the line that passes through (-3, -2), you are looking at the x value which is -3, therefore x=-3
finding an angle measure given extended triangles
answer pls ? & dnt play around .. i really need this done :/

Answers
Answer:
x = 180 - 32 - 43 - 72 = 33°
Given f(x) = ex and g(x) = x -2, what is the range of (gºf)(x)?
Answers
Answer:
y>-2
Step-by-step explanation:
Answer on E2020
Answer:
The correct answer is D) y>-2
Step-by-step explanation:
Edge 2021.
\(\int\limits^5_1 {x^2+2x-tanx} \, dx\)
Answers
The definite integral for this problem has the result given as follows:
\(\int_1^5 x^2 + 2x - \tan{x} dx = 212 - \ln{|\sec{5}|} + \ln{|\sec{1}|}\)
How to solve the definite integral?The definite integral for this problem is defined as follows:
\(\int_1^5 x^2 + 2x - \tan{x} dx\)
We have an integral of the sum, hence we can integrate each term, and then add them.
For the first two terms, applying the power rule, the integrals are given as follows:
Integral of x² = x³/3.Integral of 2x = 2x²/2 = x².The integral of the tangent is given as follows:
ln|sec(x)|
Then the integral is given as follows:
I = x³/3 + x² - ln|sec(x)|, from x = 1 to x = 5.
Applying the Fundamental Theorem of Calculus, the result of the integral is obtained as follows:
I = 5³/3 + 5² - ln|sec(5)| - (1³/3 + 1² - ln|sec(1)|)
I = 625/3 - 1/3 + 5 - 1 - ln|sec(5)| + ln|sec(1)|
I = 208 + 5 - 1 - ln|sec(5)| + ln|sec(1)|
I = 212 - ln|sec(5)| + ln|sec(1)|.
More can be learned about definite integrals at https://brainly.com/question/22008756
#SPJ1
Need some more help with Algebra

Answers
Answer:
5 nickels12 dimesStep-by-step explanation:
You have 17 nickels and dimes totaling $1.45 in value, and you want to know the number of each.
SetupLet d represent the number of dimes. Then 17-d is the number of nickels and the value in cents is ...
10d +5(17 -d) = 145
Solution5d +85 = 145 . . . . . . . simplify
5d = 60 . . . . . . . . . . subtract 85
d = 12 . . . . . . . . . divide by 5
17 -d = 17 -12 = 5 . . . . . number of nickels
Joseph has 5 nickels and 12 dimes.
The accompanying technology output was obtained by using the paired data consisting of foot lengths (cm) and heights (cm) of a sample of 40 people. Along with the paired sample data, the technology was also given a foot length of 20.4cm to be used for predicting height. The technology found that there is a linear correlation between height and foot length. If someone has a foot length of 20.4 cm, what is the single value that is the best-predicted height for that person?
Answers
The best-predicted height for someone with a foot length of 20.4 cm is approximately 65.83 cm.
To find the best-predicted height for someone with a foot length of 20.4 cm, we need to use the linear regression equation that relates foot length and height. The linear regression equation is of the form:
y = a + bx
where y is the predicted height, x is the foot length, a is the y-intercept, and b is the slope of the regression line.
From the given information, we know that the technology found a linear correlation between height and foot length. This means that we can use the paired data to calculate the values of a and b in the regression equation.
Using the paired data and technology, we can obtain the following regression equation:
height = 34.774 + 1.4966 (foot length)
Now we can substitute the given foot length of 20.4 cm into the equation to obtain the predicted height:
height = 34.774 + 1.4966 (20.4)
height = 65.83 cm
Therefore, the best-predicted height for someone with a foot length of 20.4 cm is approximately 65.83 cm.
Know more about linear regression here:
https://brainly.com/question/29665935
#SPJ11
unction g is a transformation of the parent tangent function such that
. Which graph represents function g?
A.
The graph shows trigonometric functions intercept the x-axis at minus 3, 0.2, and 3.5 units also pass parallel to the g of the x-axis.
B.
The trigonometric functions intercept the x-axis at minus 4.2, minus 1.1, 2, and 5 units also pass parallel to the g of the x-axis.
C.
The trigonometric functions intercept the x-axis at minus 3.5, minus 0.2, and 3 units also pass parallel to the g of the x-axis.
D.
The trigonometric functions intercept the x-axis at minus 5, minus 2, 1, and 4.2 units also pass parallel to the g of the x-axis.
Answers
Answer:
A.
The graph shows trigonometric functions intercept the x-axis at minus 3, 0.2, and 3.5 units also pass parallel to the g of the x-axis.
PLEASE HURRY IM TIMED
If significant digits are used to compute the product of 0.105 and 1000.2000, how many significant digits are there in the answer?
A. 0
B. 1
C. 2
D. 3
Answers
The product of 0.105 and 1000.2000 has three significant digits.
The answer is D. 3.
To determine the number of significant digits in the product of 0.105 and 1000.2000, we need to consider the rules for significant figures in multiplication.
In multiplication, the result should have the same number of significant digits as the measurement with the fewest significant digits. Let's analyze the given numbers:
0.105 has three significant digits (leading zeros are not significant).
1000.2000 has eight significant digits.
When multiplying these numbers, the product is 105.02100. The measurement with the fewest significant digits is 0.105 with three significant digits. Therefore, the product should also have three significant digits to maintain accuracy and precision.
Hence, the answer is D. 3. The product of 0.105 and 1000.2000 has three significant digits. It's important to consider significant figures in calculations to ensure the appropriate level of precision and avoid introducing misleading or inaccurate information.
To learn more about the significant digits;
https://brainly.com/question/28993414
#SPJ1
Two minor league baseball players got a total of 390 hits. Washington had 2 more hits than Sanchez. Find the number of hits for each player.
Washington had
hits. Sanchez had
hits
Answers
9514 1404 393
Answer:
Washington had 196 hitsSanchez had 194 hitsStep-by-step explanation:
Let s represent the number of hits Sanchez had. Then Washington had (s+2) hits, and their hit total was ...
s +(s+2) = 390
2s = 388 . . . . . . subtract 2
s = 194 . . . . . . . . divide by 2
Sanchez had 194 hits; Washington had 196.
What is B H and area of the parallelogram

Answers
Answer:
see below
Step-by-step explanation:
The base is 16ft
The height is 10 ft
We can find the area by
A = bh
A = 10*16 = 160 ft^2
What is the next term in the pattern? 1,1,5,17,71,247
Answers
Answer: 1085
Step-by-step explanation:
in the same sq garden plot (w/ an area of 400 sq ft) deer fencing priced at $1.50 per ft is to be installed around the plot. if sales tax is 7% how much will the fencing material cost? do not round
Answers
Given that in the same square garden plot (with an area of 400 sq ft);
\(\text{Area A = 400ft}^2=l^2\)The length of the sides of the square garden is;
\(\begin{gathered} l^2=400 \\ l=\sqrt[]{400} \\ l=20ft \end{gathered}\)The perimeter of the square field is;
\(undefined\)
Look at rectangle PQRS below. If point S is reflected over the y-axis, what would be the coordinates of the reflection of
point S?
a) ( -1,3)
b) (-4,3)
c) (4,-3)
d) (4,-6)

Answers
Answer:
it's c
Step-by-step explanation:
Answer:
C
Step-by-step explanation: