what is 5x-2y= -4 in slope intercept form
Answers
Answer:
Step-by-step explanation:

Answer:
12
Step-by-step explanation:
Related Questions
Help fast please!!!!

Answers
Answer:
0.98
Step-by-step explanation:
Compliment of getting a $20 = 1 - 0.02 = 0.98
ASAP HELP PLEASE PLEASE

Answers
Answer:
2079
Step-by-step explanation:
is the correct answer 2079
Find equations of the normal plane and osculating plane of the curve at the given point. x = 5 sin(3t), y = t, z = 5 cos(3t): (0, π,-5) find equation of the normal plane and osculating plane of the curve at the given point.x= 5 sin(3t), y= t, z= 5 cos(3t); (0, phi, -5) normal plane =osculating plane=
Answers
The equation of the osculating plane is 24x + 12√10(y-π) - 3z - 6π√10 = 0.
Given curve, x=5sin(3t), y=t, z=5cos(3t); (0, π,-5).
To find the normal plane equation, the unit normal vector of the curve at the point must first be found. The unit tangent and unit binormal vectors are both derived from the unit tangent vector.
To calculate the tangent vector, the following steps are taken:
Equation of the curve is given as,
x=5sin(3t),
y=t,
z=5cos(3t).
Differentiating above equation with respect to t, we get;
dx/dt = 15 cos(3t)
dy/dt = 1
dz/dt = -15 sin(3t)
The unit tangent vector T is given by,
T = 1/√(dx/dt² + dy/dt² + dz/dt²) (dx/dt i + dy/dt j + dz/dt k)
Substituting the given values, we get
T = (3√10/10) i + (1/√10) j - (3/√10) k
Since we have to find the normal vector, we will differentiate the unit tangent vector,T, to get the unit normal vector N.
Let's differentiate T to obtain N:
dn/dt = 1/√(dx/dt² + dy/dt² + dz/dt²) [d²x/dt² i + d²y/dt² j + d²z/dt² k] + {(-1/2)(2t)(2t')/√(dx/dt² + dy/dt² + dz/dt²)³} [dx/dt i + dy/dt j + dz/dt k]
On substituting, we get,
N = (-9/√10) i + (3√10/10) j + (9/√10) k
Therefore, the normal plane equation is given by,(-9/√10)(x) + (3√10/10)(y-π) + (9/√10)(z+5) = 0.
To find the osculating plane equation, the coordinates of the point of tangency (P) and the principal normal vector, N, are required.
The equation of the osculating plane is then written as follows:
xT + yN = c,
where c is a constant value that is calculated by substituting the coordinates of P into the equation.Let us calculate the value of P and N,
To find the value of P, we substitute t=π in the given curve,
Thus,
x(π) = 5sin(3π) = 0,y(π) = π,z(π) = 5cos(3π) = -5
Therefore, the point of tangency P is (0, π, -5).
From the above derivation, we know that the unit normal vector N is(-9/√10) i + (3√10/10) j + (9/√10) k
Therefore, the unit principal normal vector is given by,
B = T x N= [(3√10/10) i + (1/√10) j - (3/√10) k] x [- (9/√10) i + (3√10/10) j + (9/√10) k]
= [(3√10/10) (9/√10) + (3/√10) (3/√10)] i + [(9/√10) (1/√10) - (3√10/10) (- 3/√10)] j + [(1/√10) (- 3/√10) - (3√10/10) (3√10/10)] k
= (24/√10) i + (12√10/10) j - (3/√10) k
The osculating plane equation is given by,
xT + yB = c
Now substituting x=0, y=π and z=-5 in above equation, we get
c = π(12√10/10) = (6π√10/5)
For similat question on derivation
https://brainly.com/question/28527987
#SPJ11
On the first day, 8 adult tickets were sold and 13 student tickets were sold for a total of $75. On day two, 10 adult tickets were sold and 9 student tickets were sold for a total of $72. What is the cost of an adult ticket? What is the cost of a student ticket?
Answers
Step-by-step explanation:
8x + 13y = 75 (×10)
10x + 9y = 72 (×8)
80x + 130y = 750
-) 80x + 72y = 576
58y = 174
y = 3
10x + 9(3) = 72
10x + 27 = 72
10x = 72 - 27
10x = 45
x = 4.5
adult = $4.50
student = $3
A survey on a sample of 35 new cars b eing sold at a lo cal auto dealer was conducted to see which of three p opular options: Air-conditioning (A), Blueto oth (B), and Rear Camera (C), were already installed. The survey found: 18 had A, 13 had B, 12 had C,5 had A and B, 8 had A and C, 6 had B and C, 4 had all three options.
Find the numb er of cars that had:
(a) A and B but not C,
(b) A and C but not B,
(c) B and C but not A;
(d) only one of the options;
(e) at least one option;
(f ) exactly two options;
(g) none of the options.
Answers
5/14= h/16. WHAT IS H?
Answers
Answer:
40/7 = h
Step-by-step explanation:
Answer:
x = \(5\frac{5}{7}\)
Step-by-step explanation:
Consider the interaction of two species of animals in a habitat. We are told that the change of the populations x(t) and y(t) can be modeled by the equations dt
dx
=6x−2.5y
dt
dy
=−0.8x+3y
1. What kind of interaction do we observe?
Answers
The interaction observed between species X and species Y is commensalism, which is an interaction between two species in which one species benefits from the other without causing any harm to it. Commensalism is a type of symbiotic relationship
Given that the change in populations of two species of animals in a habitat can be modeled by the following equations:
\frac{dx}{dt}=6x-2.5y \frac{dy}{dt}=-0.8x+3y
The interaction that we observe between the two species can be explained as follows:
Species X has a positive coefficient in the equation of its population, which means that the population size of this species increases as it is isolated from the other species (y=0).
This indicates that species X is an intraspecific interaction, which means that it can survive and increase in numbers without the presence of another species.
Species Y, on the other hand, has a negative coefficient in the equation of its population, which means that its population size decreases when it is isolated from the other species (x=0).
This indicates that species Y is an interspecific interaction, which means that it needs the presence of another species (species X) to survive and increase in numbers.
In conclusion, we can say that the interaction observed between species X and species Y is commensalism, which is an interaction between two species in which one species benefits from the other without causing any harm to it. Commensalism is a type of symbiotic relationship.
Learn more about: commensalism
https://brainly.com/question/15045964
#SPJ11
A local tutorial franchise offers an SAT Prep course. Students begin by taking a pre-test. After taking the course, students take the SAT. The pre-test score and SAT score were recorded for 8 randomly selected students. The results were tabulated, and they produced the following results: Test Statistic: -2.06, P-value: 0.0391 At the 0.05 level of significance, test the claim that the Prep course produces an overall increase in scores. (Treat the pre-test as Population #1.)
Answers
To test the claim that the Prep course produces an overall increase in scores, we can perform a paired t-test. The null hypothesis, denoted as H₀, assumes that there is no overall increase in scores, while the alternative hypothesis, denoted as H₁, assumes that there is an overall increase in scores.
Given the test statistic of -2.06 and a p-value of 0.0391, we compare the p-value to the significance level of 0.05. Since the p-value (0.0391) is less than the significance level (0.05), we reject the null hypothesis.
Therefore, we have sufficient evidence to support the claim that the Prep course produces an increase in scores.
To learn more hypothesis click here:brainly.com/question/29576929
#SPJ11
Write a quadratic function that only has one root
Answers
Answer:
y= x squared.
Step-by-step explanation:
When graphed, the parabola only has an x-intercept at (0,0). Since a root is another word for an x-intercept, it only has one root.
I hope this helps, and I hope you have a good day.
What is the difference quotient for the function f (x) = negative startfraction 1 over 5 x minus 12 endfraction?
Answers
The difference quotient of f(x) is \(\frac{-\frac{1}{h}+ 5}{5x+ h -12}\) .
According to the given question.
We have a function
f(x) = -1/(5x -12)
As we know that, the difference quotient is a measure of the average rate of change of the function over and interval.
The difference quotient formula of the function y = f(x) is
[f(x + h) - f(x)]/h
Where,
f(x + h) is obtained by replacing x by x + h in f(x)
f(x) is a actual function.
Therefore, the difference quotient formual for the given function f(x)
= [f(x + h) - f(x)]/h
= \(\frac{\frac{-1}{5(x+h)-12} -\frac{-1}{5x-12} }{h}\)
= \(\frac{\frac{-1}{5x + 5h -12}+\frac{1}{5x-12} }{h}\)
= \(\frac{\frac{-1+5h}{5x + 5h-12} }{h}\)
= \(\frac{-1+5h}{(5x +h-12)(h)}\)
= \(\frac{-1+5h}{5xh + h^{2} -12h}\)
= \(\frac{h(-\frac{1}{h}+5) }{h(5x+h-12)}\)
= \(\frac{-\frac{1}{h}+ 5}{5x+ h -12}\)
Hence, the difference quotient of f(x) is \(\frac{-\frac{1}{h}+ 5}{5x+ h -12}\) .
Find out more information about difference quotient here:
https://brainly.com/question/18270597
#SPJ4
The points T, U, V and W all lie on the same line segment, in that order, such that the ratio of TU:UV: VW is equal to 2:5:5.2:5:5. If TW=60, find UV.
Answers
Given information:
Points T, U, V, and W all lie on the same line segment, and
\(TU:UV:VW = EditCopy equationRemove\) \(2:5:5.2:5:5.\)
If \(TW = 60\), find UV.
Solution:
As we know,
\(TU:UV:VW = 2:5:5\)
Thus,
\(TU/UV = 2/5UV/VW\)
\(= 5/5 = 1\)
We know that
\(TU + UV + VW = TW + TV\)
Substituting values,
we get
\(2k + 5k + 5k = 60 + TV\)
\(12k = 60 + TVk = 5 + TV/12\)
Therefore, \(UV = 5k\)
Using the value of k,
we get
\(UV = 5 × (5 + TV/12) = 25 + 5TV/12\)
Hence,
\(UV = 25 + 5TV/12,\)
when\(TW = 60\) is given.
Answer:
\(2\(TU:UV:VW = 2:5:5.2:5:5. TU/UV = 2/5UV/VW = 5/5 = 112k = 60 + TVk = 5 + TV/125 + 5TV/12\)\)
To know more about line segment,visit:
https://brainly.com/question/30072605
#SPJ11
The length of the line segment UV is 24.59 units (approx).
Given that T, U, V and W are points that lie on the same line segment in that order such that the ratio of TU : UV : VW is equal to 2 : 5 : 5.2 : 5 : 5.
If TW = 60, we need to find UV.We know that the ratio of TU : UV : VW is equal to 2 : 5 : 5.2 : 5 : 5.
Let TU = 2x, UV = 5x and VW = 5.2x
We know that TW = TU + UV + VW
Substitute the values of TU, UV and VW in the above equation.
60 = 2x + 5x + 5.2x60
= 12.2xx = 60 / 12.2
= 4.918UV
Distance between U and V is UV = 5x = 5 × 4.918 = 24.59 (approx)
Therefore, the length of the line segment UV is 24.59 units (approx).
To know more about length, visit:
https://brainly.com/question/32060888
#SPJ11
Someone please help for 15 points!!!
Answers
Answer:
With what nothing there
Step-by-step explanation:
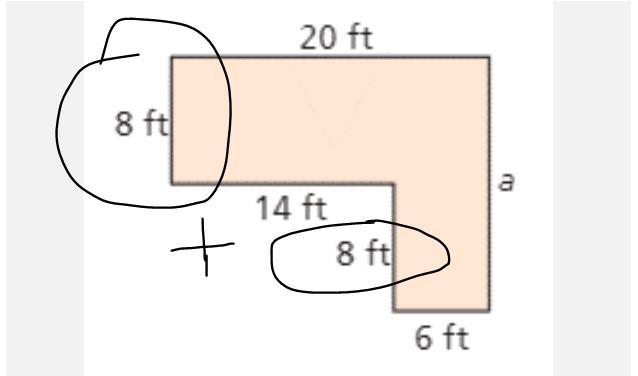
Mrs. Rios put a wallpaper border around the room shown below. She used 70 feet of wallpaper border. What is the unknown side length?
Answers
Answer: 16 feet
Step-by-step explanation:
Looking at the shape, one can notice that the unknown side can be found by adding the sides that are circled because they will give the same distance.
The length of the unknown side is therefore:
= 8 + 8
= 16 feet
Helpppppp pleaseeee thank you

Answers
The second YES
The third NO
The forth YES
Find the value of x so that line m is parallel to line l.

Answers
Explanation:
The angles shown are same side interior angles.
For line L to be parallel to line M, the same side interior angles must be supplementary, or they must add to 180.
28+(3x+14) = 180
28+3x+14 = 180
3x+42 = 180
3x = 180-42
3x = 138
x = 138/3
x = 46
Step-by-step explanation:
the angles are same side interior angles and because of that they are supplementary and add up to 180°
(3x + 14) + 28 = 180°
3x + 14 + 28 = 180
3x + 42=180
3x=180-42
3x= 138
divide by 3
x = 46
Use the order pairs to write a function rule. Give the tule in slope-intercept form.
{(-12,1.5),(-1,-1.25),(5,-2.75),(8,-3.5)}
Answers
to get the equation of any straight line, we simply need two points off of it, so hmmm let's use say (-1 , -1.25) and (8 , -3.5)
\((\stackrel{x_1}{-1}~,~\stackrel{y_1}{-1.25})\qquad (\stackrel{x_2}{8}~,~\stackrel{y_2}{-3.5}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{-3.5}-\stackrel{y1}{(-1.25)}}}{\underset{run} {\underset{x_2}{8}-\underset{x_1}{(-1)}}}\implies \cfrac{-3.5+1.25}{8+1}\implies \cfrac{-2.25}{9}\implies -\cfrac{~~ \frac{225}{100}~~}{\frac{9}{1}} \\\\\\ -\cfrac{225}{100}\cdot \cfrac{1}{9}\implies -\cfrac{9}{4}\cdot \cfrac{1}{9}\implies -\cfrac{1}{4}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-1.25)}=\stackrel{m}{-\cfrac{1}{4}}(x-\stackrel{x_1}{(-1)}) \\\\\\ y+1.25=-\cfrac{1}{4}(x+1)\implies y+\cfrac{5}{4}=-\cfrac{1}{4}x-\cfrac{1}{4} \\\\\\ y=-\cfrac{1}{4}x-\cfrac{1}{4}-\cfrac{5}{4}\implies y=-\cfrac{1}{4}x-\cfrac{6}{4}\implies y=-\cfrac{1}{4}x-\cfrac{3}{2}\)
23 times 36485290/36488719967+465778265478+124364886-8887777771830
Answers
Answer:
44
Step-by-step explanation:
Answer:
hahaha you're terriable at this
Step-by-step explanation:
find the value of x
(7x + 23)
(21x - 11)
Answers
Answer:
=30x
=10x
Step-by-step explanation:
7x + 23 = 30x
21x - 11 = 10x
p (x) = - 2/3x^2 compare the graph of f (x) = x ^2
Answers
Answer:
p(x) is reflected over the x axis and is shrunken vertically by a factor of 2/3.
Step-by-step explanation:
Hope this helps.
Estimate the difference to the nearest tentu 72.78-6.28
Answers
To estimate the difference to the nearest tenth for 72.78 - 6.28, we need to perform the following steps:Step 1: Round the decimal values to the nearest tenth 72.78 rounds to 72.8, and 6.28 rounds to 6.3.
Step 2: Subtract the rounded values 72.8 - 6.3 = 66.5 Therefore, the estimated difference to the nearest tenth for 72.78 - 6.28 is 66.5. The difference can be further rounded to a whole number if required.In 100 words:To find the estimated difference to the nearest tenth for 72.78 - 6.28, we first round the decimal values to the nearest tenth. We round 72.78 to 72.8 and 6.28 to 6.3. Then, we subtract the rounded values to get the estimated difference. This gives us the result of 72.8 - 6.3 = 66.5.
Therefore, the estimated difference to the nearest tenth for 72.78 - 6.28 is 66.5. We can round this value to the nearest whole number if required.
To know more about Whole number visit-
https://brainly.com/question/29766862
#SPJ11
Find the measure of the missing angle.

Answers
Answer:
a = 34
Step-by-step explanation:
Tell me in the comments if you want an explanation!
Hope This Helps! •v•
.Reasoning Determine the value(s) of k for which 3x² + kx + 12 = 0 has each type of solution.
a. no real solutions.
Answers
The quadratic equation 3x² + kx + 12 = 0 will have no real solutions when the discriminant (b² - 4ac) is negative.
The discriminant of the quadratic equation is given by the formula
Δ = b² - 4ac, where a = 3, b = k, and c = 12.
For the equation to have no real solutions, the discriminant must be negative. Therefore, we have:
b² - 4ac < 0
k² - 4(3)(12) < 0
k² - 144 < 0
To find the values of k that satisfy this inequality, we can solve for k:
k² < 144
|k| < \(\sqrt{144}\)
|k| < 12
This means that the value of k must lie between -12 and 12 (excluding -12 and 12) for the quadratic equation 3x² + kx + 12 = 0 to have no real solutions.
Learn more about quadratic equations here:
https://brainly.com/question/27924357
#SPJ4
If you were required to survey Fresno City College students regarding their employment status, which sampling technique would you use? Explain.
Answers
If I were required to survey Fresno City College students regarding their employment status, I would use a stratified random sampling technique.
Stratified random sampling involves dividing the population into subgroups, or strata, based on certain characteristics that are relevant to the survey. In this case, the relevant characteristic is employment status. The population consists of all Fresno City College students, and the two strata are employed and unemployed students.
Once the population has been divided into strata, a random sample is taken from each stratum. The sample size for each stratum is proportional to the size of the stratum in the population. For example, if 60% of Fresno City College students are employed, then 60% of the sample should consist of employed students.
Using a stratified random sampling technique ensures that the sample is representative of the population and that each subgroup is represented in the sample. It also reduces sampling error and increases the precision of the estimates.
Look at this table: x 19 5 19 y 2 5 8 Is this relation a function? yes no
Answers
Answer:
no
Step-by-step explanation:
Answer: No
Step-by-step explanation:
Solve the equation -4x+3y=12 for y.
Answers
$10 for 4 cans of soup what is the ratio
Answers
The ratio of cost to the number of cans = 5: 2
What is the ratio:A ratio is a mathematical concept that represents the relationship between two or more values.
In the given problem, the ratio represents the relationship between the cost of the soup and the number of cans purchased.
Ratios are commonly used in mathematics, finance, and other fields to express comparisons and relationships between different quantities.
Here we have
$10 for 4 cans of soup
The required ratio can be formed as follows
=> 10: 4
=> 10/2: 4/2 [ Divided by 2 ]
=> 5: 2
Therefore,
The ratio of cost to the number of cans = 5: 2
Learn more about Ratios at
https://brainly.com/question/26172684
#SPJ1
use stokes' theorem to evaluate counterclockwise line integralf · dr where f = yz, 2xz, exy and c is the circle x2 y2 = 25, z = 9, traversed counterclockwise when viewed from above.
Answers
Using Stokes' theorem, we can evaluate the counterclockwise line integral of the vector field F = (yz, 2xz, exy) around the circle x^2 + y^2 = 25, z = 9 when viewed from above. The result of the line integral is 900πe.
Stokes' theorem relates the line integral of a vector field around a closed curve to the surface integral of the curl of the vector field over the surface bounded by that curve. In this case, we are given the vector field F = (yz, 2xz, exy) and the circle C defined by the equation x^2 + y^2 = 25, z = 9. The circle C lies in the xy-plane and is viewed counterclockwise from above.
To apply Stokes' theorem, we first need to calculate the curl of F. The curl of F is given by the determinant:
curl(F) = (∂/∂x, ∂/∂y, ∂/∂z) x (yz, 2xz, exy) = (0, -ex, -e + 2x).
Next, we find the surface S bounded by the circle C. Since C lies in the xy-plane, S is the portion of the plane z = 9 that is enclosed by the circle C. The normal vector n to S is (0, 0, -1) since the surface is oriented downward.
Now, we can calculate the surface integral of curl(F) over S. Since the curl of F is (0, -ex, -e + 2x) and the normal vector is (0, 0, -1), the surface integral simplifies to ∫∫S (0, -ex, -e + 2x) · (0, 0, -1) dA = ∫∫S (e - 2x) dA.
Since S is a circle of radius 5 centered at the origin, we can use polar coordinates to evaluate the surface integral. Let r be the radial distance and θ be the angle. The limits of integration are 0 ≤ r ≤ 5 and 0 ≤ θ ≤ 2π. The element of area dA in polar coordinates is r dr dθ.
Evaluating the surface integral, we have ∫∫S (e - 2x) dA = ∫0^5 ∫0^2π (e - 2r cosθ) r dθ dr.
Integrating with respect to θ first, we get ∫0^5 2πr(e - 2r) dr = 2π(e∫0^5 r dr - 2∫0^5 r^2 dr).
Evaluating the integrals, we have 2π(e(5^2/2) - 2(5^3/3)) = 2π(e(25/2) - (250/3)) = 900πe/6 - 500π = 900πe - 3000π/6 = 900πe - 500π.
Therefore, the counterclockwise line integral of F around the circle C is 900πe - 500π, which simplifies to 900πe.
To learn more about Stokes' theorem click here, brainly.com/question/32258264
#SPJ11
To which subset(s) of real numbers does V30 belong?
Rational
Negative Integer
Integer
Irrational

Answers
Step-by-step explanation:
√30 is an irrational number
it belong to Irrational subset
which number produces an irrational answer when added to 3/4
Answers
Answer
pi.
Step-by-step explanation:
If you add pi (3.14) to 3/4, you will get an irrational answer.
what is the critival value for constructing a 98confidwence interval for a mean from a sampkle size of n = 15
Answers
The critical value for constructing a 98% confidence interval for a mean from a sample size of n = 15 is 2.602.
The range of values that is likely to contain the population parameter with a specific degree of certainty is known as the confidence interval. It is the range of values in which a population parameter is predicted to exist based on a sample of data. In statistical research, confidence intervals are frequently used to indicate the accuracy of an estimate or the variability of a particular statistic.
The critical value is the number used to determine if the null hypothesis should be accepted or rejected in a statistical hypothesis test. It is frequently determined using a table of critical values that corresponds to a specific level of significance and degrees of freedom.
The significance level is typically established at 5% or 0.05.
The formula to compute the critical value for a confidence interval is as follows:
Critical value = Zα/2, where Zα/2 is the Z-score associated with a level of significance of α/2.
In this case, the critical value for constructing a 98% confidence interval for a mean from a sample size of n = 15 is 2.602.
Learn more about: confidence interval - https://brainly.com/question/31325787
#SPJ11
The critical value for constructing a 98% confidence interval for a mean from a sample size of n = 15 can be found using the t-distribution table. Here are the steps to find the critical value:
1. Determine the degrees of freedom (df) for your sample size: df = n - 1 = 15 - 1 = 14.
2. Identify the confidence level: 98%.
3. Find the corresponding t-value in the t-distribution table for 98% confidence level and 14 degrees of freedom.
Upon looking up the t-distribution table, the critical value (t-value) for a 98% confidence interval with 14 degrees of freedom is approximately 2.977.
So, the critical value for constructing a 98% confidence interval for a mean from a sample size of n = 15 is 2.977.
To learn more about " Critical value for constructing a 98 confidence interval " visit : https://brainly.com/question/27125917
#SPJ11