what is (567x237)x(467x939)
i will mark brainliest
Answers
Answer:
58926938427
Step-by-step explanation:
Answer:
Folow the PEMDAS rules wich show the order in which to do things:
Parenthesis first, then Exponent, then Multiplication/Division and finally Additiion and Subtraction. Therefore we solve whats in parenthesis first then work from there
567x237 is 134,379 and 467x939 is 438,513
now that we solved whats in parenthesis multiply the remaining values:
134,379x438,513=58,926,938,427
58,926,938,427 is correct
Step-by-step explanation:
Related Questions
00:00
Select all the values of p that are solutions for this inequality
10p - 8 >12
A. -1
B. 0
C. 1
D. 2
E. 3
Answers
Answer:
The answer is D. and E.
Step-by-step explanation:
The answer is D and E because 10 multiplied by 2 is 20 and 20 is bigger then 12 and 10 times 3 is 30 which is also bigger than 12.
P.S Can I have brainliest?
From the region (2, ∞) of the inequality the values -1, 0, and 2 are not in the region, but the value 3 is in the region so p = 3 is the solution to the inequality option (E) is correct.
What is inequality?It is defined as the expression in mathematics in which both sides are not equal they have mathematical signs either less than or greater than, known as inequality.
We have inequality:
10p - 8 >12
10p > 12 + 8
10p > 20
p > 2
p ∈ (2, ∞)
Thus, from the region (2, ∞) of the inequality the values -1, 0, and 2 are not in the region, but the value 3 is in the region so p = 3 is the solution to the inequality option (E) is correct.
Learn more about the inequality here:
brainly.com/question/19491153
#SPJ2
Assume x and y are two odd numbers and x/y is an integer.
Which of the following statements are true?
I. x + y is odd
2. xy is odd.
3. x/y is odd
4. x-y is odd
Answers
Answer:
Let us check these out one at a time:
1. x + y is odd. FALSE. The sum of 2 odd numbers is even.
2. xy is odd. TRUE. The product of 2 odd numbers is odd.
3. x/y is odd. TRUE. The ratio of 2 odd numbers is odd, if the ratio is an integer.
4. x - y is odd. FALSE. The difference of 2 odd numbers is even.
Only statements 2 and 3 are TRUE, so that makes (C) the correct answer.
On a coordinate plane, a line with positive slope goes through points A and B. Point A is at (0, negative 2) and point B is at (3, 0). Use the graph of the line shown to determine its slope. The slope of line AB is .
Answers
According to the given information, the slope of line AB is \(\frac{2}{3}\).
What is the slope?
The slope of a line is a measure of how steep the line is. It tells us how much the y-coordinate of the line changes for each unit of change in the x-coordinate.
To visualize a slope, imagine a line on a coordinate plane. If the line is steep, it means that for each unit of increase in the x-coordinate, the y-coordinate changes by a larger amount. Conversely, if the line is less steep, it means that for each unit of increase in the x-coordinate, the y-coordinate changes by a smaller amount.
To find the slope of a line that passes through two given points, we use the slope formula:
\(slope = \frac{(change in y) }{(change in x)}\)
In this case, we have points A(0, -2) and B(3, 0).
So the change in y is 0 - (-2) = 2, and the change in x is 3 - 0 = 3.
Therefore, the slope of line AB is:
\(slope = \frac{(change in y) }{(change in x)} = \frac{2}{3}\)
Since the slope is positive, we know that the line slants upwards as we move from left to right on the coordinate plane.
To know more about slope visit:
brainly.com/question/3493733
#SPJ1
2+2=
a. 3
b. 5
c. 4
d. 7
Answers
Answer:
C
Step-by-step explanation:
2
+2
-----
4
The graph below is a polynomial function in the form f(x)=(x−a)(x−b). Find suitable real numbers a and b that describe the graph.

Answers
a and b are the values for x when y=0
GHS has vertices (3.0.5.3 and 54 State the coordinates of the image of GHS after the transformation below D₂ o T(-3,1) Your answer
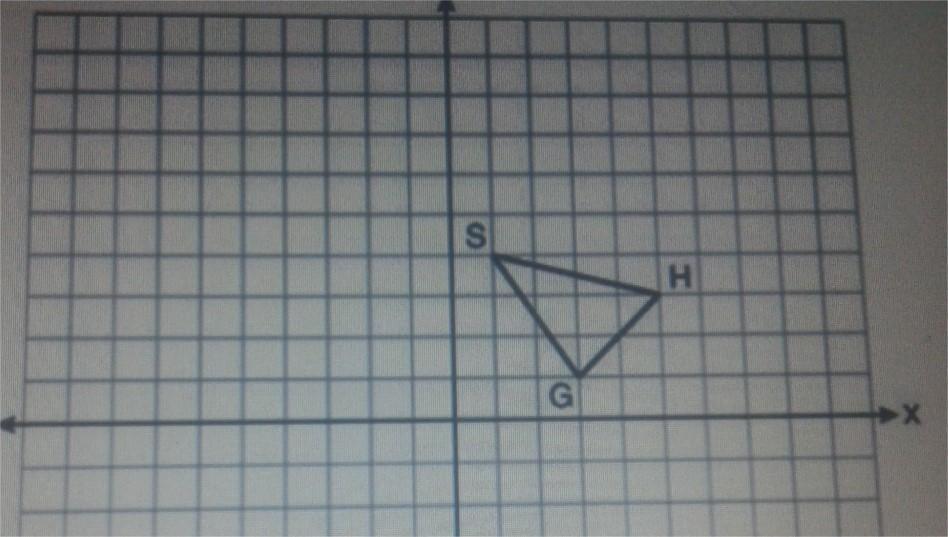
Answers
We have a triangle GHS which will be transformed by a dilation by a factor of 2, with center at (0,0) and a translation of (-3,1).
We can find the coordinates of a point (x,y) after the dilation of factor 2 as:
\(P=(x,y)\longrightarrow P^{\prime}=(2x,2y)\)Then, the translation can be described as:
\(P^{\prime}=(2x,2y)\longrightarrow P^{\prime}^{\prime}=(2x-3,2y+1)\)Then, for points G(3,1), H(5,3) and S(1,4), the transformations will result in:
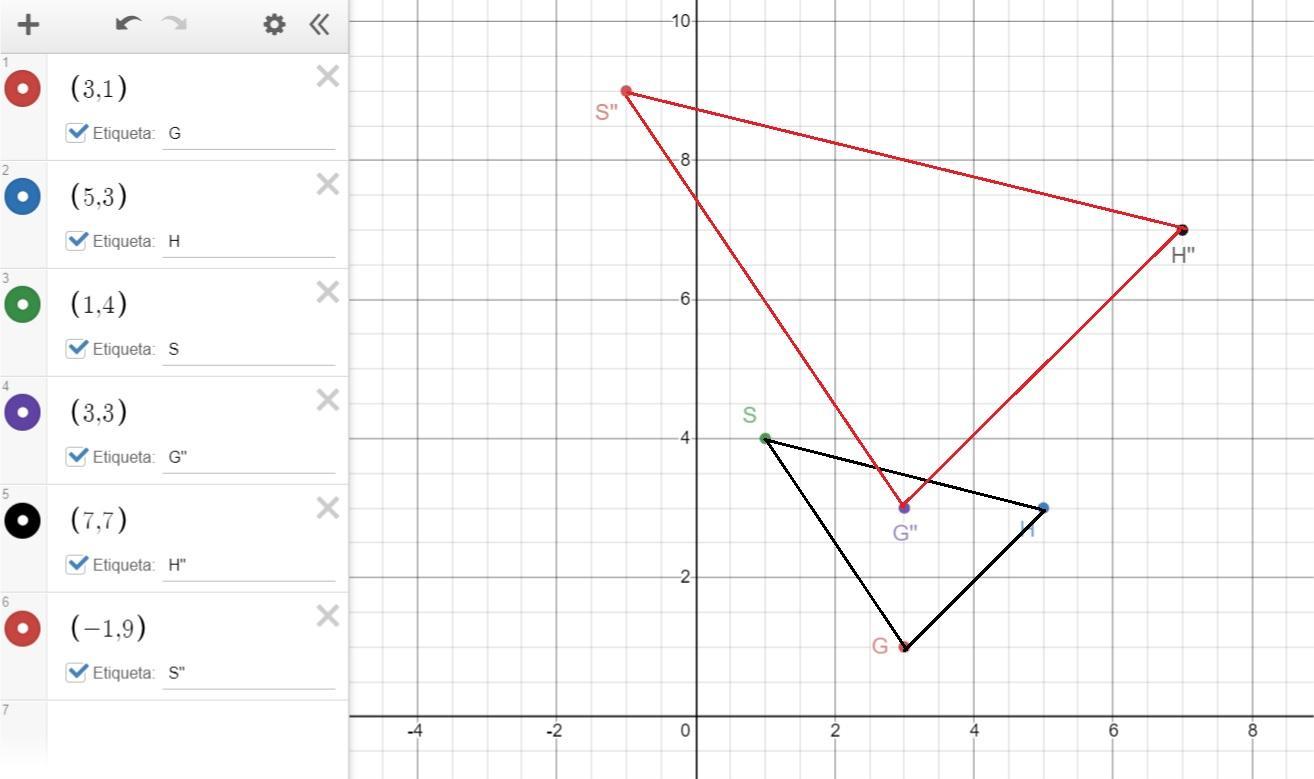
\(\begin{gathered} G=(3,1)\longrightarrow G^{\prime\prime}=(2\cdot3-3,2\cdot1+1)=(3,3) \\ H=(5,3)\longrightarrow H^{\prime\prime}=(2\cdot5-3,2\cdot3+1)=(7,7) \\ S=(1,4)\longrightarrow S^{\prime\prime}=(2\cdot1-3,2\cdot4+1)=(-1,9) \end{gathered}\)We can see the transformation in the graph as:
Answer:
Coordinates after the transformation:
G''=(3,3)
H''=(7,7)
S''=(-1,9)
Stephen has a rectangular rug with a perimeter of 16 feet the width of the rug is 5 feet what is the length of the rug
Answers
The length of Stephen's rug is 3 feet.
How can you use the perimeter and width of Stephen's rug to find the length?To find the length of Stephen's rug, we can use the formula for the perimeter of a rectangle, which is P = 2L + 2W, where P is the perimeter, L is the length, and W is the width. In this case, we know that the perimeter of the rug is 16 feet and the width is 5 feet. So, we can plug in these values into the formula and solve for L:
Let's use the formula for the perimeter of a rectangle to solve the problem: Perimeter = 2 x (Length + Width)
We know that the perimeter of the rug is 16 feet and the width is 5 feet. Plugging those values into the formula, we get: 16 = 2 x (Length + 5)
Simplifying the equation, we can divide both sides by 2:
8 = Length + 5
16 = 2L + 2(5)
16 = 2L + 10
2L = 6
L = 3
Therefore, the length of Stephen's rug is 3 feet.
To know more about Perimeter visit:
brainly.com/question/15287805
#SPJ1
Please help urgent thank you

Answers
If he wants an average of 84, he needs to get at least 93 points.
What score does he need to get in the next test?Remember that the average value between 3 values A, B, and C is:
(A + B + C)/3
Here we know that the first two scores are 76 and 83 points, let's say that the third score is x, if we want to have an average of 84 or more, then we need to solve:
(76 + 83 + x)/3 = 84
159 + x = 252
x = 252 - 159
x = 93
So he needs to get at least 93 points in the next exam.
Learn more about averages at:
https://brainly.com/question/20118982
#SPJ1
Solve the equation 12v+10v+14=80
Answers
Answer:V=3
Step-by-step explanation:
Step 1: Simplify both sides of the equation.
12v+10v+14=80
(12v+10v)+(14)=80
(Combine Like Terms)
22v+14=80
22v+14=80
Step 2: Subtract 14 from both sides.
22v+14−14=80−14
22v=66
Step 3: Divide both sides by 22.
22v/22=66/22
V=3
:)
r3 – [q + (r – s)2 ]
Answers
The expression is simplified to r²( r + 1) - (q - s²)
What are algebraic expressions?Algebraic expressions are mathematical expressions made up of variables and constants.
They are mostly made up of algebraic operations such as addition, subtraction, division, multiplication, bracket, parenthesis, etc
Given the expression;
r3 – [q + (r – s)2 ]
With the knowledge of BODMAS, we expand the bracket
r³ - q + ( r + s²)
r³ - q + r² - s²
Now, let's collect like terms
r³ + r² - q - s²
(r³ + r²) - (q - s²)
Factor out r, we then have;
r²( r + 1) - (q - s²)
The expression is simplified to r²( r + 1) - (q - s²)
Thus, the expression is simplified to r²( r + 1) - (q - s²)
Learn more about algebraic expressions here:
https://brainly.com/question/4344214
#SPJ1
(1 point) A bucket that weighs 3.6 pounds and a rope of negligible weight are used to draw water from a well that is 78 feet deep. The bucket is filled with 38 pounds of water and is pulled up at a rate of 2.9 feet per second, but water leaks out of a hole in the bucket at a rate of 0.1 pounds per second. Find the work done pulling the bucket to the top of the well. Your answer must include the correct units. (You may enter lbf or lb*ft for ft-lb.)
Answers
Answer:
The total work done in pulling the bucket to the top of the well is approximately 3,139.1 ft·lb
Step-by-step explanation:
The given parameters are;
The mass of the bucket, W = 3.6 pounds
The depth of the well, h = 78 feet deep
The mass of water in the bucket = 38 ponds
The rate at which the water is pulled up = 2.9 feet per second
The rate at which water is leaking from the bucket, \(\dot m\) = 0.1 pounds per second
We separate and find the work done for lifting the bucket and the water individually, then we add the answers to get the solution to the question as follows;
The work done in lifting bucket empty from the well bottom, \(W_b\) = W × h
∴ \(W_b\) = 3.6 pounds × 78 feet = 280.8 ft-lb
The work done in lifting bucket empty from the well bottom, \(W_b\) = 280.8 ft-lb
The time it takes to lift the bucket from the well bottom to the top, 't', is given as follows;
Time, t = Distance/Velocity
The time it takes to pull the bucket from the well bottom is therefore;
t = 78 ft./(2.9 ft./s) ≈ 26.897
The time it takes to pull the bucket from the well bottom to the top, t ≈ 26.897 s
The mass of water that leaks out from the bucket before it gets to the top, m₂, is therefore;
m₂ = \(\dot m\) × t
∴ m₂ = 0.1 lbs/s × 26.897 s = 2.6897
The mass of the water that leaks, m₂ = 2.6897 lbs
The mass of water that gets to the surface m₃ = m - m₂
∴ m₃ = 38 lbs - 2.6897 lbs ≈ 35.3103 lbs
Given that the water leaks at a constant rate the equation representing the mass of the water as it is lifted can b represented by a straight line with slope, 'm' given as follows;
The slope of the linear equation m = (38 lbs - 35.3103 lbs)/(78 ft. - 0 ft.) = 0.03448\(\overline 3\) lbs/ft.
Therefore, the equation for the weight of the water 'w' can be expressed as follows;
w = 0.03448\(\overline 3\)·y + c
At the top of the well, y = 0 and w = 38
∴ 35.3103 = 0..03448\(\overline 3\) × 0 + c
c = 35.3103
∴ w = 0.03448\(\overline 3\)·y + 35.3103
The work done in lifting the water through a small distance, dy is given as follows;
(0.03448\(\overline 3\)·y + 38) × dy
The work done in lifting the water from the bottom to the top of the well, \(W_{water}\), is given as follows;
\(W_{water} = \int\limits^{78}_0 {0.03448\overline 3 \cdot y + 35.3103 } \, dy\)
\(\therefore W_{water} = \left [ {\dfrac{0.03448\overline 3 \cdot y^2}{2} + 35.3103 \cdot y\right ]^{78}_0\)
\(W_{water}\) = (0.034483/2 × 78^2 + 35.3103 × 78) - (0.034483 × 0 + 38 × 0) ≈ 2,859.1
The work done in lifting only the water, \(W_{water}\) ≈ 2,859.1 ft-lb
The total work done, in pulling the bucket to the top of the well, W = \(W_b\) + \(W_{water}\)
∴ W = 2,859.1 ft.·lb + 280.8 ft.·lb ≈ 3,139.1 ft·lb
The total work done, in pulling the bucket to the top of the well, W ≈ 3,139.1 ft·lb.
I need help plz help me!!!!

Answers
Can you guys help me pls

Answers
Explanation: When answering a question like this check to see if the line is a negative slope : or a positive slope:
use the steps: RISE-over-RUN
FOR EXAMPLE- this would be rise 3 run 1
3/1 or 3 :)
Find the value of x in the parallelogram

Answers
The value of x in the parallelogram is 112°.
In a parallelogram, adjacent angles are always supplementary. This means that the sum of two adjacent angles in a parallelogram is always 180 degrees.
To understand this concept, let's consider a parallelogram ABCD. The opposite sides of a parallelogram are parallel and equal in length, and the opposite angles are congruent. Adjacent angles are those that share a side. Let's say angle A and angle B are adjacent angles in the parallelogram.
Since opposite angles of a parallelogram are congruent, we have angle A is congruent to angle C, and angle B is congruent to angle D.
Now, let's consider angle A and angle B. The sum of angle A and angle B is equal to the sum of angle C and angle D because opposite angles are congruent.
Therefore, we can conclude that angle A + angle B = angle C + angle D = 180 degrees.
This property holds true for all parallelograms. So, in any parallelogram, the adjacent angles are always supplementary, meaning their sum is 180 degrees.
For the given question, we know x° + 68° = 180°.
Then x° = 180° - 68°
x° = 112°
For more such questions on parallelogram
https://brainly.com/question/20526916
#SPJ8
The expression (picture below) is equivalent to...
PLEASE HELP! I REALLY NEED IT!
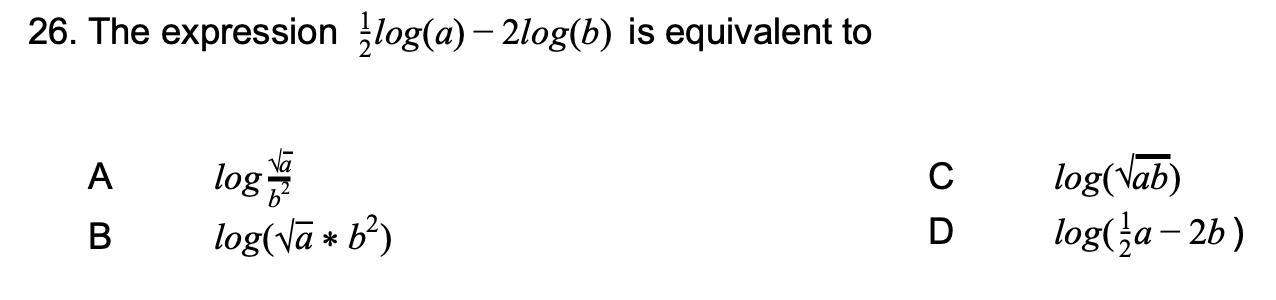
Answers
Answer:
Step-by-step explanation:
go to this website Cymath.com
2radical3+3radical2
Rationalize the denominator (simplify)
(3-√2
Answers
Step-by-step explanation:
ucixidepchflgkckcudkchdkgldjcisifiic
Crystal has 6 3/4 pints of lemonade that she will pour into mugs for her classmates at the end of the year party
Each mug holds 3/8 of a pint. if she pours all of the lemonade how many mugs she need, including any mug that maybe only partially filled
Answers
Answer:
18 mugs
Step-by-step explanation:
first let's convert 6 3/4 into eights. 6 3/4 as an improper fraction is 27/4, which we multiply by 2 to get 54/8. now we do 54 divided by 3, since we can now ignore the denominator. 54 divided by 3 = 18. This is divided evenly so the "including mugs that are partially filled" is a red herring.
Reuben made a shirt using 7/8yards of red fabric and 1/4yards of yellow fabric. How many more yards of red fabric did Reuben use?
Answers
Answer and Step-by-step explanation:
To find out how many more yards of red fabric Reuben used, we need to subtract the amount of yellow fabric from the amount of red fabric. Since the two fractions have different denominators, we need to find a common denominator before subtracting them. The least common multiple of 8 and 4 is 8, so we can rewrite both fractions with a denominator of 8:
7/8 - 1/4 = 7/8 - (1/4) * (2/2) = 7/8 - 2/8 = (7 - 2)/8 = 5/8
So, Reuben used 5/8 yards more red fabric than yellow fabric.
Question: 18 of 19
Lesson 18
Find the component form of the following vectors. Round your answers to the tenth.
Magnitude of v = 50, direction angle 0 = 50°
Choice 'A' OV
Choice 'B'O V
Choice 'C'OV
Choice 'D' OV
(38.3, 32.1)
(33.8, 31.2)
(32.1, 38.3)
(31.2, 33.8)
4

Answers
The component form of the following vectors is Option A. V = (38.3, 32.1).
To find the component form of a vector given its magnitude and direction angle, we can use trigonometry.
The component form of a vector in two dimensions is represented as (x, y), where x is the horizontal component and y is the vertical component.
In this case, the magnitude of the vector is given as 50, and the direction angle θ is 50°. We can use this information to calculate the horizontal and vertical components.
The horizontal component (x) can be found using the formula x = magnitude * cos(θ), and the vertical component (y) can be found using y = magnitude * sin(θ).
Let's calculate the components:
x = 50 * cos(50°) ≈ 38.3
y = 50 * sin(50°) ≈ 32.1
Rounding the answers to the nearest tenth, we get the component form of the vector V as (38.3, 32.1).
Therefore, the correct answer is A. V = (38.3, 32.1).
Know more about the vectors here:
https://brainly.com/question/30854499
#SPJ8
The question is incomplete. Find the full content below:
Find the component form of the following vectors. Round your answers to the tenth.
Magnitude of v = 50, direction angle θ = 50°
A. V = (38.3, 32.1)
B. V = (33.8, 31.2)
C. V = (32.1, 38.3)
D. V = (31.2, 33.8)
Geometry Section 58C/School Year/
For the three-part question that follows, provide your answer to each part in the given workspace. Identify each part with a coordinating response. Be sure to clearly label each part of your response as Part A
Part B, and Part C
Part A: How many triangles can be formed if the measurements of a triangle are a 27,6-15, A-557
Part B: Explain how to determine the answer to Part A
Part C: Find all possible solutions for this triangle.
BiFont Family -AA-A
11
P Type here to search
ii
LE
8
DELL
I
PREVIOUS
19 of 23
NEXT
nomad
SAVE & EXT
3:00 PM
3/14/2023

Answers
1. Triangle inequality theorem.
3. The missing lengths and angles are:
<B = 27.07, <C = 98 and c = 32.64.
1. According to triangle inequality theorem, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
2. To determine the number of triangles that can be formed, we can use the given measurements and check if the triangle inequality theorem is satisfied.
3. We have,
a = 27, b = 15, and A = 55°,
Using the Law of Sines,
sin A/ a = sin B/ b
sin 55 /27 = sin B / 15
0.81915204428 / 27 = sin B /15
0.4550844690444 = sin B
<B = 27.07
Now, <C = 180 - <A - <B = 180 - 55 - 27.07 = 98
Now, Using the Law of Sines
sin A/ a = sin C/ C
0.81915204428 / 27 = sin 98 / c
0.030338964602963 = 0.99026807 /c
c = 32.64
Learn more about Sine Law here:
https://brainly.com/question/13098194
#SPJ1
Maria is studying the phenomenon of pyramid power. She has read that items placed inside pyramids show amazing properties. Maria is going to see if the pyramid phenomenon will work on her young plants. She will construct an all-glass pyramid as shown.
The pyramid is regular with a square base, and all eight edges are the same length. From the possible solutions below, which amount is the closest estimate of the amount of glass Maria will need to construct her pyramid?
a) 1935 cm squared
b) 3353 cm squared
c) 5289.25 cm squared
d) 8642.5 cm squared

Answers
The solution that is the closest estimate of the amount of glass Maria will need to construct her pyramid would be =5289.25 cm squared. That is option C.
How to calculate the area of a square based pyramid?To calculate the area of a square based pyramid, the formula that should be used would be given below as follows:
\(area = {a}^{2} + 2a \sqrt{ \frac{a2}{4} } + {h}^{2} \)
Where:
a= 44cm
height= 44²-22²= 38.1cm
Area= 44²+ 2(44) × √44²/4 + 38.1²
= 1936+88 × √ 484+1452
= 2024× √1936
= 5807.61 cm².
Therefore the closest estimate to the final answer would be 5289.25 cm squared
Learn more about area here:
https://brainly.com/question/28470545
#SPJ1
Which angles below are equal to ∠CDB?

Answers
Answer:
(x) ∠CAB
Step-by-step explanation:
In ΔCOD and ΔBOA
\(\frac{OA}{OB} = \frac{OD}{OC} \\\\\implies \frac{OC}{OB} = \frac{OD}{OA}\)
Also,
∠COD = ∠BOA (vertically opposite angles)
⇒ ΔCOD and ΔBOA are similar
⇒ ∠CDO = ∠BAO
⇒ ∠CDB = ∠BAC
⇒ ∠CDB = ∠CAB
Katelyn had 2 dogs and 3 cats. Which of the following shows the ratio written correctly for the number of dogs to cats?
A) 3:2
B) 3-2
C) 2:3
D) 3 x 2
Answers
Answer:
2:3
Step-by-step explanation:
Ratio is indicated by :
Its dogs to cats, right so ratio is number of dogs:number of cats which is 2:3
Hope this helps plz mark brainliest if correct :D
Answer:
2:3
Step-by-step explanation:
2 is first and 3 is the second number so you put them in order
please help me solve that question

Answers
Step-by-step explanation:
\(\sin(\theta + \phi) = 2\cos(\theta - \phi)\)
Using the addition identity formulas, we can write
\(\sin{\theta}\cos{\phi} + \cos{\theta}\sin{\phi} = 2\cos{\theta}\cos{\phi} + 2\sin{\theta}\sin{\phi}\)
Dividing both sides by \(\cos{\phi}\), we get
\(\sin{\theta} + \cos{\theta}\tan{\phi} = 2\cos{\theta} + 2\sin{\theta}\tan{\phi}\)
Dividing both sides by \(\sin{\theta}\), we get
\(\tan{\theta} + \tan{\phi} = 2 + 2\tan{\theta}\tan{\phi}\)
or
\(\tan{\theta}(1 - 2\tan{\phi}) = 2 - \tan{\phi}\)
Rearranging the terms,
\(\tan{\theta} = \dfrac{2 - \tan{\phi}}{1 - 2\tan{\phi}}\)
pls helllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllp
The cost of 4 ice cream cones from the snack bar was $10.40. If each ice cream cone costs the same amount, which model correctly illustrates the relationship? Check all that apply.
y = 10.4 x
y = 2.6 x
y = 4 x
Cost of Ice Cream Cones
A 2-column table with 3 rows. Column 1 is labeled number of ice cream cones with entries 13, 26, 39. Column 2 is labeled Total cost (in dollars) with entries 5, 10, 15.
Cost of Ice Cream Cones
A 2-column table with 3 rows. Column 1 is labeled number of ice cream cones with entries 5, 10, 15. Column 2 is labeled Total cost (in dollars) with entries 13, 26, 39.
Cost of Ice Cream Cones
On a coordinate plane, the x-axis is labeled number of ice cream cones and the y-axis is labeled total cost (in dollars). A line goes through points (0, 0) and (5, 13).
Cost of Ice Cream Cones
On a coordinate plane, the x-axis is labeled number of ice cream cones and the y-axis is labeled total cost (in dollars). A line goes through points (3, 1) and (18, 7).
Answers
Step-by-step explanation:
The model that illustrates the relationship is 4x=10.404x=10.40
The cost of each ice cream was x=\$2.60x=$2.60
Step-by-step explanation:
Let
x----> the cost of one ice cream
we know that
The linear equation that represent this situation is
4x=10.404x=10.40
solve for x
Divide by 4 both sides
x=10.40/4x=10.40/4
x=\$2.60x=$2.60
Answer:
First answer is y = 2.6 (or answer two)
Second answer is Cost of Ice Cream Cones
A 2-column table with 3 rows. Column 1 is labeled number of ice cream cones with entries 5, 10, 15. Column 2 is labeled Total cost (in dollars) with entries 13, 26, 39. (or the first mini graph-ish thingy, i don't remember what to call it)
Third answer is
Cost of Ice Cream Cones
On a coordinate plane, the x-axis is labeled number of ice cream cones and the y-axis is labeled total cost (in dollars). A line goes through points (0, 0) and (5, 13). (or the first graph)
Step-by-step explanation:
Correct on edge 2021
and i did the calculations
I hope this helped have a great day!
You have a bag of different flavored candies. The probabilities of randomly selecting a particular flavor of candy are shown below:
Cherry | .245
Lime | .325
Lemon | .180
Orange | .215
Grapefruit | .035
Your buddy Earl likes the lime candies. He eats a bunch of them and hands the bag back to you. The complement of the event P(selecting a Lime candy from the bag) would:
A. become 0
B. stay the same
C. There isn't enough information to answer this question
D. increase
E. decrease
(according to a different site E. decrease isn't the answer)
Answers
The complement of the event P(selecting a Lime candy from the bag) would increase.
The probability of event P(selecting a Lime candy from the bag) would decrease after Earl eats a bunch of lime candies.
In essence, the complement of the event P(selecting a Lime candy from the bag), which is synonymous to the chance of not picking a Lime candy from the bag increases.
Read more:
https://brainly.com/question/52529
The currency exchange rate is 1 United States Dollar equals 0.87 Euro. If Anna buys a dress that costs her $65 in US Dollars, how much will it cost her in Euros?
Answers
Answer:
56.55
Step-by-step explanation:
65*.87
Since speed is equal to distance divided by time, what would distance be equal to?
Answers
The in this case, the distance covered by the car would be 120 miles. The equation Distance = Speed * Time allows us to determine the distance covered by an object when the speed and time taken are known.
To determine distance, we can rearrange the formula for speed:
Speed = Distance / Time. By multiplying both sides of the equation by Time, we can isolate Distance.
Distance = Speed * Time
The formula indicates that distance is equal to the product of speed and time. By multiplying the rate at which an object moves (speed) by the duration of travel (time), we can determine the total distance covered during that period.
The equation Distance = Speed * Time represents the relationship between distance, speed, and time.
It states that the distance covered is equal to the product of the speed at which an object is moving and the time it takes to travel that distance.
For example, if a car is traveling at a constant speed of 60 miles per hour for 2 hours, the distance it would cover can be calculated as follows:
Distance = 60 miles/hour * 2 hours = 120 miles.
For more such questions on Distance:
https://brainly.com/question/28551043
#SPJ8
AB and CD are tangents of circle O find each of the following

Answers
The lines CA and CD are tangents to the circle O, hence; EA = 4, AB = 15, m∠ABO = 90°, m∠ODC = 90°, and m∠EAB = 30°.
Tangent to a circle theoremThe tangent to a circle theorem states that a line is tangent to a circle if and only if the line is perpendicular to the radius drawn to the point of tangency
If OB = 6 and AB = 8, then;
OA = √(8² + 6²) {by Pythagoras rule}
OA = √100
OA = 10
EA = OA - OE(radius)
EA = 10 - 6 = 4
If DE = 16 and EA = 9, then;
OA = (diameter/2) + EA
OA = 8 + 9 = 17
AB = √(17² - 8²)
AB = √225
AB = 15
OB is perpendicular to line CA tangent to the circle so m∠ABO = 90°
OD is perpendicular to the line CD tangent to the circle so m∠ODC = 90°
If m∠DOB = 120° then;
120° = m∠ABO + m∠EAB {exterior angle of a triangle is equal to the two opposite interior angles}
m∠EAB = 120° - 90°
m∠EAB = 30°
In conclusion, for the lines tangent to the circle, we have that;
EA = 4, AB = 15, m∠ABO = 90°, m∠ODC = 90°, and m∠EAB = 30°
Know more about tangent to a circle here:https://brainly.com/question/11067500
#SPJ1
what is between fractions 6/6 and 6/7
Answers
The fraction 13/7 lies between the fractions 6/6 and 6/7.
We have,
Between the fractions 6/6 and 6/7, there are infinitely many fractions.
To find a fraction that lies between these two fractions, we can take their average.
The fraction 6/6 simplifies to 1, and the fraction 6/7 cannot be simplified further.
To find the average, we add the two fractions and divide the sum by 2:
(6/6 + 6/7) / 2
To add the fractions, we need a common denominator, which is the least common multiple (LCM) of 6 and 7, which is 42.
Converting the fractions to have a common denominator:
(6/6) x (7/7) + (6/7) x (6/6) / 2
Simplifying the expression:
(42/42 + 36/42) / 2
Combining the numerators:
(78/42) / 2
Dividing:
78/42 = 13/7
Thus,
The fraction 13/7 lies between the fractions 6/6 and 6/7.
Learn more about fractions here:
https://brainly.com/question/24370499
#SPJ1