what is 2(3x+4)=x-7
Answers
Related Questions
PLEASE answer pic provided

Answers
Answer:
50 to 60 seconds is the answer
As the CAPS document outlines, the Content Specification and Content Clarification for Patterns, Functions, and Algebra shows sequenced mathematics content topics and a content area spread. In the Intermediate Phase, select one topic and report on the topic sequence and content area spread. Your report should demonstrate mathematics concepts and procedures’ hierarchical and logical progression.
Answers
Answer:
Step-by-step explanation:
In the Intermediate Phase of mathematics education, one topic that demonstrates a hierarchical and logical progression in patterns, functions, and algebra is the concept of "Linear Equations."
The topic of Linear Equations in the Intermediate Phase builds upon the foundation laid in earlier grades and serves as a stepping stone towards more advanced algebraic concepts. Here is an overview of the topic sequence and content area spread for Linear Equations:
Introduction to Variables and Expressions:
Students are introduced to the concept of variables and expressions, learning to represent unknown quantities using letters or symbols. They understand the difference between constants and variables and learn to evaluate expressions.
Solving One-Step Equations:
Students learn how to solve simple one-step equations involving addition, subtraction, multiplication, and division. They develop the skills to isolate the variable and find its value.
Solving Two-Step Equations:
Building upon the previous knowledge, students progress to solving two-step equations. They learn to perform multiple operations to isolate the variable and find its value.
Writing and Graphing Linear Equations:
Students explore the relationship between variables and learn to write linear equations in slope-intercept form (y = mx + b). They understand the meaning of slope and y-intercept and how they relate to the graph of a line.
Systems of Linear Equations:
Students are introduced to the concept of systems of linear equations, where multiple equations are solved simultaneously. They learn various methods such as substitution, elimination, and graphing to find the solution to the system.
Word Problems and Applications:
Students apply their understanding of linear equations to solve real-life word problems and situations. They learn to translate verbal descriptions into algebraic equations and solve them to find the unknown quantities.
The content area spread for Linear Equations includes concepts such as variables, expressions, equations, operations, graphing, slope, y-intercept, systems, and real-world applications. The progression from simple one-step equations to more complex systems of equations reflects a logical sequence that builds upon prior knowledge and skills.
By following this hierarchical progression, students develop a solid foundation in algebraic thinking and problem-solving skills. They learn to apply mathematical concepts and procedures in a systematic and logical manner, paving the way for further exploration of patterns, functions, and advanced algebraic topics in later phases of mathematics education.
At the start of a game of marbles, Peter and Jack had 160 marbles in all. In the first round, Peter lost 3/5 of his marbles to Jack. In the second round, James lost 3/7 of his marbles to Peter. At the end of the second round of the game, they had the same number of marbles. How many marbles did each of them have at first?
Answers
Answer: Therefore, at the start of the game, Peter had 80 marbles and Jack had 80 marbles.
Step-by-step explanation:
HELP ME FIGURING OUT THE ANSWER !! ASAP !!

Answers
Answer C -16 is the answer
I got that answer by doing ( -8 x 2 ).
Simply it’s ( -8 x 2= -16 ) |AB| essentially means you’re multiplying the two numbers.
Miranda has a home-based business making and selling scented soaps. She initially spent $60 to purchase soap-making equipment, and the materials for each kilogram of soap cost $13. Miranda sells the soap for $19 per kilogram. Eventually, she will sell enough soap to cover the cost of the equipment. How much soap will that be?
Answers
The total amount of soap that needs to be sold in order to cover the cost of the equipment is 10 kilograms.
What are equations?Two things are equal, according to an equation. The equals sign "=" will appear as in the formula: x + 2 = 6.
According to that equation, what is on the right is equivalent to what is on the left (x + 2).
A mathematically based fact or rule is called a formula.
Typically, it will have: two or more variables (x, y, etc.) with the equals symbol (=) representing values we don't yet know
A statement like "this equals that" is an equation.
Let the amount of soap in kilogram = x.
Given that, She initially spent $60 to purchase soap-making equipment, and the materials for each kilogram of soap cost $13. This is represented as:
A = 60 + 13x
She sells the soap for $19"
S = 19x
To cover the cost the initial investment must be equal to the number of soap sold:
60 + 13x = 19x
60 = 6x
x = 10
Hence, the total amount of soap that needs to be sold in order to cover the cost of the equipment is 10 kilograms.
Learn more about equations here:
https://brainly.com/question/29657983
#SPJ1
The perimeter of a rectangle is 79cm. One side is three times the length of the other. From an equation and hence find the length of each side
Answers
Answer:
Step-by-step explanation:
Make the length of one side = 'x'
The other side = 3xPerimeter = 2 x one side + 2 x the other side
79 cm = 2(x) + 2(3x)
79 cm = 2x + 6x
8x = 79
x = 9.875
One side = 9.875 cm
Other side = 29.625 cm
Matthew is saving money for a pet turtle the data in the table represents the total amount of money in dollars that he saved by the end of each week.
Answers
NO LINKS!!
Write a mathematical model for the problem and solve it.
The sum of two consecutive natural numbers is 575. Find the numbers. (Enter your answers as a comma-separated list.)
Answers
Answer:
Step-by-step explanation:
To find the two consecutive natural numbers whose sum is 575, we can set up the following equation:
x + (x+1) = 575
where x and x+1 are the two consecutive natural numbers.
We can solve this equation by combining like terms:
2x + 1 = 575
Subtracting 1 from both sides, we get:
2x = 574
Dividing both sides by 2, we get:
x = 287
Therefore, the two consecutive natural numbers are 287 and 288. Our final answer is 287, 288.
Answer:
287,288
Step-by-step explanation:
Question
The sum of two consecutive natural numbers is 575. Find the numbers
soln
x +( x + 1) = 575
x + x + 1 = 575
2x + 1 = 575
2x = 575 – 1
2x = 574
\( \frac{2x}{2} = \frac{574}{2} \)
x = 287
since we got x as 287, lets solve(x+1)
by substituting
287 + 1 = 288
hence the consecutive numbers are 287,288
Check
287 + 288 = 575
we are correct.
i hope this helps
a) Rationalise the denominator of a,b,c

Answers
Answer:
See below
Step-by-step explanation:
a)
\( \frac{20}{ \sqrt{10} } = \frac{20 \sqrt{10} }{ \sqrt{10} \times \sqrt{10} } = \frac{20 \sqrt{10} }{10} = 2 \sqrt{10} \)
b)
\( \frac{ \sqrt{2} }{2 \sqrt{5} - 1 } \\ \\ = \frac{ \sqrt{2} \times (2 \sqrt{5} + 1 )}{(2 \sqrt{5} - 1)(2 \sqrt{5} + 1) } \\ \\ = \frac{ \sqrt{2} \times 2 \sqrt{5} + \sqrt{2} \times 1 }{(2 \sqrt{5} ) ^{2} - (1)^{2}} \\ \\ = \frac{ 2 \sqrt{10} + \sqrt{2}}{20 - 1} \\ \\ = \frac{ 2 \sqrt{10} + \sqrt{2}}{19} \\ \\ equating \: it \: with \: \\ \frac{ a + \sqrt{b}}{c} \\ \\ a = 2 \sqrt{10} \\ \\ b = 2 \\ \\ c = 19\)
Answer:
The above answer is correct
Algebra!!!
3 Questions Only take if you know ALL Answers
PLZZZ QUICK

Answers
Answer:
1. -7.5
2. $1
3. 40
Step-by-step explanation:
For number 1, it can be solved by using the PEMDAS method, or see explanation below:
6x - 4x - 36 = 6 - 2x
2x - 36= -2x + 6
4x + 36 = 6
4x = -30
x = -15/2 or -7.5
For number 2, substitute 3 into both equations:
f(x) =1.50(3) + 2.00
and
f(x) = 2.00(3) + 1.50
This would get $6.50 and $7.50, which, if subtracted, gets $1.
For number 3, do something similar to the previous problem. Substitute 3 for x. It would be 5(2^3), or 40.
Hope this helps!
Kaya babysits to add money to her savings. She draws a graph to show how much she can earn by babysitting. What is the equation of Kaya's line in slope-intercept form
Answers
Answer:
Step-by-step explanation:

Which set of numbers may represent the lengths of the sides of a triangle? (A) {2,5,9} (B) {6,6,7} (C) {6,4,2} (D) {7,8,1}
Answers
Answer:
(B) {6,6,7}
Step-by-step explanation:
A criterion to determine if each triplet represents a triangle is the Law of Cosine, which states that:
\(a^{2} = b^{2}+c^{2}-2\cdot b \cdot c \cdot \cos \theta\)
Where \(a\), \(b\) and \(c\) are sides of the triangle and \(\theta\) is the angle opposite to side \(a\). Now, let is clear the cosine function:
\(2\cdot a \cdot b\cdot \cos \theta = b^{2}+c^{2}-a^{2}\)
\(\cos \theta = \frac{b^{2}+c^{2}-a^{2}}{2\cdot b \cdot c}\)
Cosine is a bounded function between -1 and 1, a triplet corresponds to a triangle if and only if result is located between upper and lower bounds. Now let is evaluate each triplet:
a) \(a = 2\), \(b = 5\), \(c = 9\)
\(\cos \theta =\frac{5^{2}+9^{2}-2^{2}}{2\cdot (5)\cdot (9)}\)
\(\cos \theta = 1.133\) (Absurd)
The triplet does not represent a triangle.
b) \(a = 6\), \(b = 6\), \(c = 7\)
\(\cos \theta =\frac{6^{2}+7^{2}-6^{2}}{2\cdot (6)\cdot (7)}\)
\(\cos \theta = 0.583\) (Reasonable)
The triplet represents a triangle.
c) \(a = 6\), \(b = 4\), \(c = 2\)
\(\cos \theta = \frac{4^{2}+2^{2}-6^{2}}{2\cdot (4)\cdot (2)}\)
\(\cos \theta = -1\) (Absurd)
The triplet does not represent a triangle, but a straight line.
d) \(a = 7\), \(b = 8\), \(c = 1\)
\(\cos \theta = \frac{8^{2}+1^{2}-7^{2}}{2\cdot (8)\cdot (1)}\)
\(\cos \theta = 1\) (Absurd)
The triplet does not represent a triangle, but a straight line.
Hence, the correct answer is B.
Find the linear function with the following properties.
f(−3)=−12
f(−7)=4
Answers
Answer:
To find the linear function with the given properties, we need to determine the slope and y-intercept of the function.
We can use the slope-intercept form of a linear function, which is:
y = mx + b
where m is the slope and b is the y-intercept.
First, we can find the slope using the two given points:
slope = (y2 - y1) / (x2 - x1)
slope = (4 - (-12)) / (-7 - (-3))
slope = 16 / (-4)
slope = -4
Now that we have the slope, we can use one of the given points to find the y-intercept. Let's use the point (-3, -12):
y = mx + b
-12 = (-4)(-3) + b
-12 = 12 + b
b = -24
Therefore, the linear function that satisfies the given properties is:
f(x) = -4x - 24
f(x) = -4x - 24
Step by step Explanation:
To find the linear function f(x) with the given properties, we can use the point-slope form of a linear equation:
y - y1 = m(x - x1)
where m is the slope of the line and (x1, y1) is a point on the line.
Using the two given points, we can find the slope of the line:
m = (y2 - y1) / (x2 - x1)
m = (4 - (-12)) / (-7 - (-3))
m = 16 / (-4)
m = -4
Now we have the slope of the line, and we can use one of the given points to find the y-intercept:
f(x1) = y1
f(-3) = -12
So when x = -3, y = -12. We can use this point to find the y-intercept:
y - y1 = m(x - x1)
y - (-12) = -4(x - (-3))
y + 12 = -4(x + 3)
y = -4x - 24
Therefore, the linear function f(x) that satisfies the given properties is:
f(x) = -4x - 24
what is refraction
Answers
Answer:
I hope this will be the answer... ✌️

\(\large{\pmb{\underline{\underline{\sf{Refraction:-}}}}}\)
Refraction is the bending of a light or sound wave, or the way the light bends when entering the eye to form an image on the retina.
\(\large{\pmb{\underline{\underline{\sf{Examples~ Of~ Refraction:-}}}}}\)
Bending of the sun's rays as they enter raindrops, forming a rainbow.\({\huge{\underline{\small{\mathbb{\pink{HOPE \ THIS \ HELPED \ UH:)}}}}}}\)
Cheers !! :3
Is (-5, -5) a solution to this system of equations?
=
y = -x - 7
y = x-3
yes
no
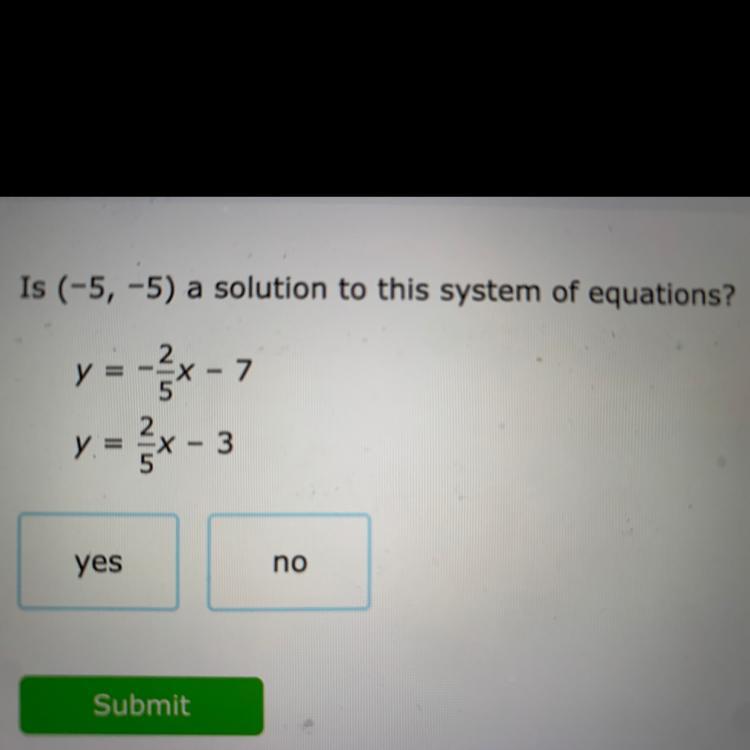
Answers
Answer:
no
Step-by-step explanation:
equate the two equations (make them equal to each other)
-2/5x - 7 = 2/5x - 3
get rid of the fractions by multiplying everything by 5
5(-2/5x - 7 = 2/5x - 3)
-2x - 35 = 2x - 15
solve
-2x - 35 = 2x - 15
-2x - 2x = -15 + 35
-4x = 20
x = -5
plug in "x" to one of the starting equations (I'm using the second one)
y = 2(-5) - 15
y = -10 - 15
y = -25
an easier way would be to plug in the point for "x" and "y"
-5 = 2(-5) - 15
-5 = -10 - 15
-5 = -25 FALSE
FIRST ONE TO GET ME THE CORRECT ANSWER WILL WIN BRAINIEST

Answers
9514 1404 393
Answer:
59 3/4
Step-by-step explanation:
The change from the opening price is ...
-50 1/2 +110 1/4 = 60 -1/4 = 59 3/4 . . . change from opening price
Owen and his children went into a restaurant where they sell hotdogs for $4 each and tacos for $2.50 each. Owen has $60 to spend and
buy a minimum of 18 hotdogs and tacos altogether. If x represents the number of hotdogs purchased and y represents the number of tac
purchased,
Answers
Answer:
Hotdogs is 10
and Tacos 8 in numbers purchased
Step-by-step explanation:
Step one:
given data
Le x represents the number of hotdogs purchased
and y represents the number of tac
hotdogs = $4 each
and tacos = $2.50 each
The total amount at hand = $60
Step two:
The systems of the equations for the situation is given as
4x+2.5y= 60---------1
x+y=18-----------------2
Required
The number of Hotdogs and Tacos purchased
from 2
x= 18-y
put x= 18-y in eqn 1
4(18-y)+2.5y= 60
72-4y +2.5y=60
collect like terms
-4y+2.5y=60-72
-1.5y= -12
divide both sides by -1.5
y= -12/-1.5
y= 8
put y= 8 in eqn 2
x+8=18
x= 18-8
x= 10
11. If AB LCD, mZDCE = (7x + 2) and mZECB= (x + 8), find the measure of ZDCE.
AC B.

Answers
Since AB is parallel to CD, we have alternate interior angles forming when transversal CE intersects the parallel lines. Therefore,
mZDCE = mZECB (Alternate Interior Angles)
(7x + 2) = (x + 8) (Substitute in the given angle measures)
Solving for x, we get:
7x + 2 = x + 8
6x = 6
x = 1
Now, we can use x to find the measure of angle ZDCE:
mZDCE = (7x + 2)
= (7*1 + 2)
= 9
Therefore, the measure of angle ZDCE is 9 degrees.
An examination paper has 150 multiple-choice questions of one mark each, with each question having four choices. Each incorrect answer fetches -0.25 mark. Suppose 1000 students choose all their answers randomly with uniform probability. The sum total of the expected marks obtained by all these students is?
Answers
The sum of expected marks is given as follows:
9375.
How to obtain the expected marks?Each question has four choices, hence the probability of choosing the correct choice is given as follows:
p = 1/4 = 0.25.
Then the expected number of correct answers is given as follows:
E(X) = 0.25 x 150
E(X) = 37.5.
Then the expected grade for a single student is given as follows:
37.5 - 0.25(150 - 37.5) = 9.375.
The expected sum for the 1000 students is then given as follows:
1000 x 9.375 = 9375.
Learn more about the concept of probability at https://brainly.com/question/24756209
#SPJ1
You put a $275 plate set on layaway and put down a 25% deposit. What is the balance?
Answers
Find the standard form of the equation of the line through (8,-3) that is parallel to the line 3y=4x+8
Answers
The standard form of the equation of the line passing through (8,-3) that is parallel to the line 3y=4x+8 is 4x - 3y = 41
How to represent equation in standard form?The equation of the line in standard form can be represented as follows:
Ax + By = C
where
A, B and C are constantTherefore, the standard form of the equation of the line through (8,-3) that is parallel to the line 3y = 4x + 8 is a s follows;
Parallel lines have the same slope.
Hence,
3y = 4x + 8
y = 4 / 3 x + 8 / 3
The slope of the line is 4 / 3. Hence, the line passes through (8, -3). let's find the y-intercept.
y = 4 / 3 x + b
-3 = 4 / 3 (8) + b
b = -3 - 32 / 3
b = -9 - 32/ 3
b = -41 / 3
Hence,
y = 4 / 3 x - 41 / 3
multiply through by 3
3y = 4x - 41
Therefore, the standard form is 4x - 3y = 41
learn more on standard form here: https://brainly.com/question/11479371
#SPJ1
A movie theater charges $7.50 for adults and $4.50 for children. For a recent showing of the movie "Maleficent," the
theater sold 43 tickets and made a total of $238.50. How many children's tickets and how many adult tickets were sold?
Answers
Answer
9 and 10
Step-by-step explanation:
Which statements are true? Check all that apply.
0 is greater than Negative two-thirds.
Two-thirds is equal to Negative two-thirds.
Negative 1 less-than negative one-third
Negative two-thirds greater-than one-third
Negative one-third greater-than negative two-thirds
(PLEASE DO NOT ANSWER IF YOU AREN'T GOING TO PUT A REAL ANSWER!!!!!)
Answers
Answer:
0 is greater than Negative two-thirds.
Negative 1 less-than negative one-third
Negative one-third greater-than negative two-thirds
Step-by-step explanation:
Two-thirds is equal to Negative two-thirds and Negative two-thirds greater-than one-third are incorrect.
Answer:
a c e
Step-by-step explanation:
What is x? Because I don’t know g how to work it out

Answers
Answer:
45 degrees
Step-by-step explanation:
The 4 angles of a quadrilateral will add to 360.
We know 1 of them (angle B) is 90 degrees.
We can set up an equation to solve the others.
2x+3x+x+90 = 360
Now solve for x.
Start by combining the x terms together.
6x+90 = 360
6x = 360-90
6x = 270
(6x/6) = 270/6
x = 45 degrees
Check back to see if that makes sense and if the equation equals 360 when x is 45:
2x+3x+x+90 = 360
2(45)+3(45)+45+90=360.
1. Out of 318 seventh and eighth grade CAVA students there were 48 students that chose Music as their elective
course and the rest chose World Language. There were a total of 124 eighth grade students and 108 of them
chose World Language as their elective.
Use this information to complete the two-way table completely.
Enter your answer by filling in the boxes to complete the table (5 pts)
Answer:
8th Grade
7th Grade
Totals
Music
48
World Language
108
Totals
124
318

Answers
The students in 8th class who choose music are 16 in number,
The students in 7th class who choose music are 32 in number
The total who choose world language is 270
The totals who are in 7th grade be 194
The number of students who choose world language in 7th class are 162
Let x be the students in 8th class who choose music
x+108=124
x=124-108
x=16 students
Now y be the students in 7th class who choose music
16+y=48
y=48-16
y=32
Let z be the total who choose world language
48+z=318
z=318-48
z=270
Now the totals who are in 7th grade be A
124+A=318
A=318-124
A=194
B be the number of students who choose world language in 7th class
Now 32+B=194
B=194-32
B=162
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
Samuel cut a cone from a piece of wood shaped as a cylinder. He measured the circumference of the base of the cylinder and found that it measured 3πinches. The height of the cylindrical piece of wood was 6 inches. What is the approximate volume of Samuel's cone if it has the same base area and height as the cylinder?
Answers
Answer:
The approximate volume of the cone is 14 cube inches.
Step-by-step explanation:
Circumference of the base of the cylinder = 3π inches
Height of the cylindrical piece of wood = 6 inches
volume of a cone = \(\frac{1}{3}\)\(\pi\)\(r^{2}\)h
But,
circumference = 2πr
3π = 2πr
r = \(\frac{3}{2}\)
= 1.5 inches
Radius of the base of the cylinder is 1.5 inches.
So that;
volume of cone = \(\frac{1}{3}\) x \(\frac{22}{7}\) x \((\frac{3}{2}) ^{2}\) x 6
= \(\frac{1}{3}\) x \(\frac{22}{7}\) x \(\frac{9}{4}\) x 6
= 14.143
volume of cone = 14.143 cube inches
The approximate volume of the cone is 14 cube inches.
Find the best approximation to a solution of the following systems of equations. What the value for y? 2x+y=-5– 2 = 82x + 3y = 1 3 O-3 4 -4
Answers
The system of equations is inconsistent and has no solution.
Here's a step by step process to check for consistency:
2x + y = -5
82x + 3y = 1
Subtracting the first equation from the second gives us:
80x + 2y = 6, which can not be true for any values of x and y.
Therefore, the system of equations has no solution and no approximation of y can be made.
The arrangement of conditions gave doesn't have an answer, since it prompts clashing responses. Basically, when we plug in values for x, the conditions offer us two unique responses for y, and that implies there is definitely not a solitary point that fulfills the two conditions. This makes it difficult to track down an incentive for y that would make the two conditions right. It's like attempting to adjust two teeter-totters simultaneously with loads, yet the loads are different on each side, making it difficult to adjust the two sides. For this situation, there is no arrangement, so finding an incentive for y that works for the two equations is impractical.
To learn more about best approximation, refer:
https://brainly.com/question/9149066
#SPJ4
2. Solve the following addition problem. Remember to carry as necessary.
6 cu yd 9 cu ft
134 cu in
+ 1 cu yd 12 cu ft
200 cu in
Answers
The solution to the given addition problem is 150.6 ft^9.
Converting everything to the same unit is the simplest solution to this problem.
The conversions are:
1 cubic yard = (27 cubic feet)
1 cubic inch = (0.000578704 cubic feet)
The addition can be performed as,
(6 cu yd × 9 cu ft × 134 cu in) + (1 cu yd × 12 cu ft × 200 cu in)
= [6(27 cu ft) × 9 cu ft × 134(0.000578704 cu ft)] + [1(27 cu ft) × 12 cu ft × 200(0.000578704 cu ft)]
= 150.6 ft^9
The result of the addition is 150.6 ft^9.
To know more about conversion of measurement visit:
https://brainly.com/question/12906576
#SPJ13
Sixty men can build a wall in 40days but though they begin the work together, 55 men quit every ten days. The Time needed to build the wall is?
Answers
It would take 370 days to build the wall with the given conditions.
If 60 men can build a wall in 40 days, then the total man-days required to build the wall is:
60 men x 40 days = 2400 man-days
However, 55 men quit every ten days, which means that after 10 days, there are only 60 - 55 = 5 men left to work on the wall. After 20 days, there are only 5 - 55 = -50 men left, which means that the remaining 5 men cannot work any faster than they were already working. Therefore, we can assume that the remaining 5 men complete the wall on their own.
The number of man-days required for the first 10 days is:
60 men x 10 days = 600 man-days
The number of man-days required for the second 10 days is:
5 men x 10 days = 50 man-days
The total number of man-days required for the first 20 days is:
600 man-days + 50 man-days = 650 man-days
The remaining work can be completed by the 5 men in:
2400 man-days - 650 man-days = 1750 man-days
Therefore, the total time needed to build the wall is:
20 days + 1750 man-days / 5 men = 20 + 350 days = 370 days
For such more questions on conditions
https://brainly.com/question/18395678
#SPJ8
Name the property shown by each statement. FAST PLSS!!!!!!!

Answers
Answer:
The answer is the Associative Property of Addition.
Step-by-step explanation:
When you add, you can group the numbers in any combanation.
Such as a + ( b + c ) = ( a + b ) + c
2p = a
3q = b
2 = c
So, if you were to write it out it would match perfectly into the format.