what is (19-y)+5y=55
Answers
Answer:
y = 9
Step-by-step explanation:
19-y+5y= 55
19+4y = 55
4y = 55 - 19
4y = 36
y = 36/4
y = 9
Related Questions
Chau will rent a car for the weekend. He can choose one of two plans. The first plan has an initial fee of $44 and costs an
additional $0.11 per mile driven. The second plan has an initial fee of $49 and costs an additional $0.07 per mile driven.
for what amount of driving to the two plans cost the same amount?
What is the cost when the two plans cost the same?
Answers
Answer:
I don't know
Step-by-step explanation:
i don't know
what is a correct name fo the angle shown. R S RTS SRT
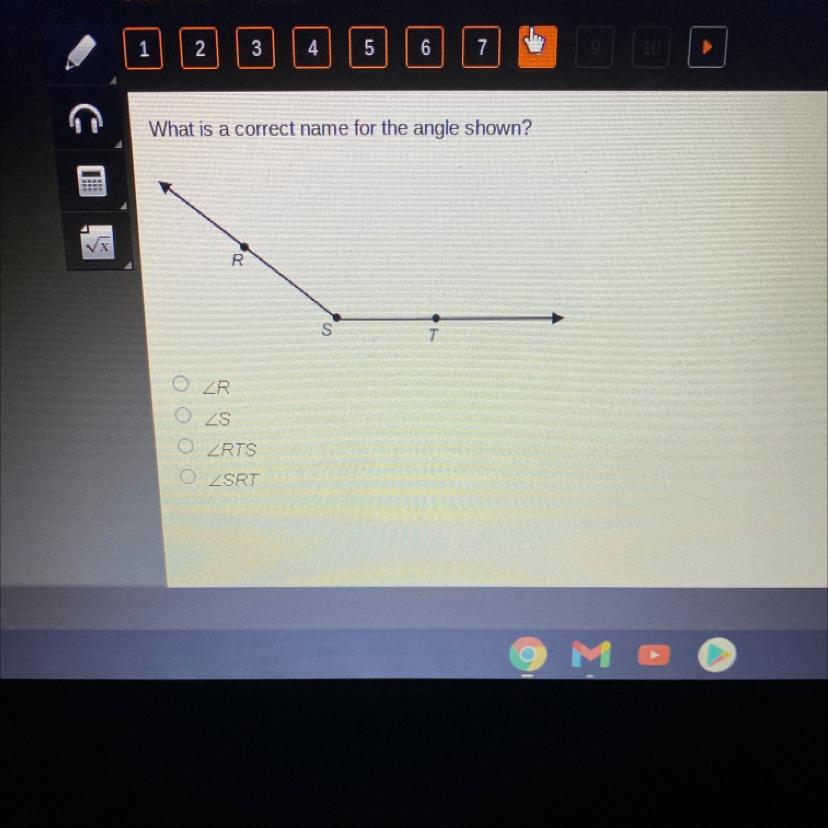
Answers
The equation is __ ( type your answer in standard form)

Answers
Answer:
In standard form, the answer should be : 2y + x = 6.
Step-by-step explanation:
See attached image.

First, find the slope of the line between the two points using
\(m = \dfrac{y_2-y_1}{x_2-x_1}\)
Then use one point to calculate the b for \(y=mx+b\).
Step 1: slope
\(\begin{aligned}m&=\dfrac{7-4}{-4-2}\\[0.5em]&=\dfrac{3}{-6}\\[0.5em]&=-\dfrac{1}{2}\end{aligned}\)
Step 2: calculate b
Right now we have \(y=\frac{1}{2}x+b\), so we'll plug in (2,4) for the x and y:
\(\begin{aligned}\\4&=-\frac{1}{2}(2)+b\\[0.5em]4&=-1+b\\[0.5em]5&=b\end{aligned}\)
Now we build our slope-intercept equation: \(y=-\frac{1}{2}x+5\)
But, this isn't standard form. We need to clear out the fraction and then move the x-term to the left.
Can you take it from there?
HURRY!!!!!!!!!!!!!!!
The table shows the proportional relationship between the number of tickets required per game at a carnival. Games 4 7 10 Tickets 20 35 50 Determine the constant of proportionality.
Correct answer will get brainiest
Answers
Answer:
Therefore, the constant of proportionality for the given proportional relationship is 5.
Step-by-step explanation:
To determine the constant of proportionality in the given proportional relationship, we can use the formula:
Constant of Proportionality = Tickets / Games
Let's plug in the values from the table:
For the first set of values (4 games and 20 tickets):
Constant of Proportionality = 20 / 4 = 5
For the second set of values (7 games and 35 tickets):
Constant of Proportionality = 35 / 7 = 5
For the third set of values (10 games and 50 tickets):
Constant of Proportionality = 50 / 10 = 5
In all three cases, the constant of proportionality is equal to 5.
Therefore, the constant of proportionality for the given proportional relationship is 5.
sound travels about 340m/s the function d(t)=340t gives the distance d(t) in meters that sound travel in t seconds how far does it travel in 37 s
Answers
What is the intermediate step in the form
(x+a)^2=b as a result of completing the square for the following question
Answers
The intermediate step in completing the square is\($x^2 + 2ax + (a^2) = b - a^2 + (a^2)$\)
To complete the square for the equation \($(x+a)^2=b$\), we can follow these steps:
1. Expand the left side of the equation: \($(x+a)^2 = (x+a)(x+a) = x^2 + 2ax + a^2$\).
2. Rewrite the equation by isolating the squared term and the linear term: \($x^2 + 2ax = b - a^2$\).
3. To complete the square, take half of the coefficient of the linear term, square it, and add it to both sides of the equation:
\($x^2 + 2ax + (a^2) = b - a^2 + (a^2)$\).
4. Simplify the right side of the equation: \($x^2 + 2ax + (a^2) = b$\).
This step can be represented as: \(\[x^2 + 2ax + (a^2) = b - a^2 + (a^2)\]\)
This intermediate step helps us rewrite the equation in a form that allows us to factor it into a perfect square.
For more such questions on intermediate step: https://brainly.com/question/30458168
#SPJ11
Find the value of x.
B
X+2
3
E
2
X
С
A
x = [?]
![Find the value of x.BX+23E2XAx = [?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/rksolRb1pogicf7WytENm6MIVx1C7XI3.png)
Answers
Answer:
answer is given in up paper. where ans is -1/2
![Find the value of x.BX+23E2XAx = [?]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/ojq3K4drS9dIBM9aDbw8xuiE0W2jevx7.jpeg)
Find m and c for this line
Y+3x=1
Answers
Answer:
m = -3 ; c = 1
Step-by-step explanation:
y = -3x + 1
y = mx + c
m = -3
c = 1
Question 7:
In the morning, the temperature starts out around 50°F. As
the day goes on, the temperature rises first slowly, then more
quickly. It stays constant for an hour before dropping slowly.
Select the graph that best represents this description.
10 AM
10 AM
127
Time
Time
BE
10 AM
12
4
Time
Time

Answers
Answer:Graph A.
Step-by-step explanation:
Graph A.
Step-by-step explanation:
We will try to understand the graph plotted for the change in temperature for whole day.
In the morning, temperature starts out around 50°F. As the day goes on, the temperature rises first slowly- Slope of the first line will be less.
Then temperature rises more quickly - Slope of the second line will be more than first line.
It stays constant for an hour- third line will be parallel to the x-axis for one hour gap.
Then the temperature dropped down slowly - Last line of the graph will go down.
By the understanding we made for the graph we find graph A is the answer.
2^3 • 3 evaluate the expression plz help me
Answers
Answer:
24
Step-by-step explanation:
2^3 * 3 = 8 * 3 = 24
Hope this helped!
Answer:
24
Step-by-step explanation:
2^3 is equal to 2 times 2 times 2 which is 8 and 8 times 3 is 24
A salesperson at a jewelry store earns 3% commission each week. Last week, Heidi sold $750
worth of jewelry. How much did she make in commission? How much did the jewelry store make
from her sales?
Heidi earned $ in commission.
Answers
Good morning helpppp new !!!

Answers
Answer:
c= 17
Step-by-step explanation:
c² = a² + b²
c= ?
a = 8
b= 15
c² = (8)² + (15)²
c² = 64 + 225
c² = 289
\( \sqrt{c ^{2} } = \sqrt{289} \\ \\ c = 17\)
Part a:Cell phone usage grew about 23% each year from 2010 to 2016. If cell phone usage in 2010 was 43 million, write a function f(x) to model U.S. cell phone usage over that time period, where x is the number of years since 2010.
Part b estimate the cell phone usage in 2013.round to the nearest ten thousand.
Answers
Answer:
The function f(x) to model U. S. cell phone usage over the time period of 2010 to 2016 can be expressed as f(x) = 43 * (1.23^x), where x is the number of years since 2010. Part b: The estimated cell phone usage in 2013 can be calculated by substituting x = 3 into the function f(x) = 43 * (1.23^x). This yields an estimated cell phone usage of 68.4 million in 2013, which can be rounded to the nearest ten thousand to 68 million.
Step-by-step explanation:
15. Graph 6 and 6 on the number line.
A++
-6 5 4 3 2 1 0 +1 +2 +3 +4 +5 +6
Page 6
Wilson says both 6 and 6 have an absolute value of 6. Is
Wilson correct? Use the number line and words to explain why
or why not.
Answers
Yes, Wilson is right since "negative numbers" don't exist when you find the absolute value.
How Do You Define Absolute Value?Without taking into account direction, absolute value describes how far a number is from zero on the number line.A number's absolute value can never be negative.A number or phrase is most frequently represented by the absolute value sign, which consists of two vertical straight lines, around it|-6| = 6 denotes that "6 is -6 in absolute terms.""The absolute value of the phrase -2 minus x" is what |-2 - x| denotes.The meaning of -|x| is "the opposite of the absolute value of x."The number line can be used to graph equalities and inequalities that contain expressions with absolute value in addition to displaying the distance from zero.Therefore, Wilson is correct as there is no negative term in absolute value.
To learn more about the number line, refer to https://brainly.com/question/25230781
#SPJ1
8x^{3} -27-4x^{2} +6x+9
Answers
Answer:solution
Step-by-step explanation:
2 (4x^3-2x^2+3x-9)
The formulas for total revenue and total cost, in hundreds of dollars, for selling and producing q hundred Items are: total revenue: TR(q) = 30q total cost: Tc(q) = q^3-15q^2+75q+10. (a) Find the smallest quantity at which marginal cost is equal to 15 dollars per Item. (b) Recall: Fixed cost is given by FC = TC(0). Variable cost is given by VC(q) = TC(q) - FC. Average variable cost is given by AVC(q) = VC(q)/q. Find a positive value of q at which average variable cost is equal to marginal cost. (c) Find the longest interval on which marginal revenue exceeds marginal cost. (d) Recall that profit is given by P(q) = TR(q)-TC(q) and On an interval of quantities where MR(q) < MC(q), profit is decreasing. On an interval of quantities where MR(q) > MC(q), profit is increasing Use the sketch you drew in part (c) to find the quantity at which profit is greatest. What is the maximum value of profit?
Answers
(a). The smallest quantity at which marginal cost is equal to 15 dollars per item is 2.76. (b). The positive value of q at which average variable cost is equal to marginal cost is \(\frac{15}{2}\). (c). The longest interval on which marginal revenue exceeds marginal cost is (1.8377, 8.1622). (d). The profit is increasing at 8.1622 at p(q) is maximum. (e). The maximum value of profit is 78.2455 dollars.
The total revenue: TR(q) = 30q
The total cost: Tc(q) = \(q^3-15 q^2+75 q+10$\)
The change in cost is referred to as the change in the cost of production when there is a need for change in the volume of production.
(a). Marginal cost MC\(=\frac{\partial}{\partial q}(T C)$\)
\($$=3q^2-30 q+75 \text {. }$$\)
According to question.
\($$\begin{aligned}& 3 q^2-30 q+75=15 \\& 3 q^2-30 q+60=0 \\& q^2-10 q+20=0 \\& q= \frac{10 \pm \sqrt{100-80}}{2} \\&= \frac{10 \pm 2 \sqrt{5}}{2}=5 \pm \sqrt{5}\end{aligned}\)
\($$$\therefore \quad q=5+\sqrt{5} \quad$ and $q=5-\sqrt{5}$\)
we have to find smallest quantity.
\($$\therefore \quad q=5-\sqrt{5}=2.76 \text {. }$$\)
b)
\($$\begin{aligned}& F C=T C(0)=10 \\& V C(q)=T C(q)-F C \\& =q^3-15 q^2+75 q . \\& \text { AVC(q) }=\frac{V C(q)}{q}=q^2-15 q+75 .\end{aligned}$$\)
When AVC(q)=MC(q)
\($$\begin{array}{ll}\Rightarrow & q^2-15 q+7 ;=3 q^2-30 q+75 \\\Rightarrow & 2 q^2-15 q=0 .\ \Rightarrow q(2 q-15)=0 . \\\Rightarrow & q=0, \frac{15}{2} \quad \Rightarrow \quad q=\frac{15}{2}\end{array}$$\)
Therefore, the positive value of q at which average variable cost is equal to marginal cost is \(\frac{15}{2}\).
(c).
\(& M R(q)=\frac{d}{d q}(T R)=30 . \\\)
\(& M C(q)=3 q^2-30 q+75 . \\\)
Let MR(a)>MC(q)
\(& \Rightarrow \quad 30 > 3 q^2-30 q+75 \text {. } \\\)
\(& \Rightarrow \quad 3 q^2-3 p q+45 < 0 \\\)
\(& \Rightarrow \quad q^2-10 q+15 < 0 \text {. } \\\)
\(& \because \quad q=\frac{10 \pm \sqrt{100-60}}{2} \Rightarrow q=\frac{10 \pm 2 \sqrt{10}}{2} \\\)
\(& q=(5 \pm \sqrt{10}) \\\)
\(& \Rightarrow \quad(q-5+\sqrt{10})(q-5-\sqrt{10}) < 0 . \\\)
\(& \Rightarrow \(q-5+\sqrt{10}) < 0 \quad \& \quad(q-5-\sqrt{10}) > 0 \text {. } \\\)
\(& \text { or } \quad(q-5+\sqrt{10}) > 0 \quad \& \quad(q-5-\sqrt{10}) < 0 \text {. } \\\)
\(& \therefore \quad \text { other } q < 5-\sqrt{10}=1.8377 ., q > 5+\sqrt{10}=8.1622 \text {. } \\\)
\(& \Rightarrow \quad q < 1.8377 \& q > 0.1622 \text {. } \\\)
\(& \text { or } q > 5-\sqrt{10} \quad \& \quad q < 5+\sqrt{10} \text {. } \\\)
\(& \Rightarrow q > 1.8377 \quad < q < 8.1622 \text {. } \\\)
The Interval is (1.8377, 8.1622).
(d). P(q) =TR(q)-TC(q)
\(& =30 q-\left(q^3-15 q^2+75 q+10\right) \\& =-q^3+15 q^2-75 q-10+30 q \\& =-q^3+15 q^2-45 q-10 .\)
on (1.8377,8.1622). we have to find a point such that p"(q)=0 and p"(q)<0.
\(& p^{\prime}(q)=-3 q^2+30 q-45 \\\)
\(& \Rightarrow \quad-3\left(q^2-10 q+15\right)=0 \\\)
\(& \Rightarrow \quad q^2-10 q+15=0 . \\\)
\(& \quad q=1.8377 \text { and } \quad q=8.1622 . \\\)
\(& \Rightarrow \quad p^{\prime \prime}(q)=-6 q+30 . \\\)
\(& p^{\prime \prime}(1.8377)=-6(1.8377)+30 \\\)
\(&=18.9738 \\\)
\(& p^{\prime \prime}(8.1622)=-6(8.1622)+30 . &=-18.9732 < 0 .\)
at 8.1622, p(q) is maximum.
(e).
Max profit-P(8.1622)
=78.2455 dollars
Therefore, the maximum value of profit is 78.2455 dollars.
For more such questions on Marginal cost
https://brainly.com/question/16027422
#SPJ4

(Angles in
The figure shows a parallelogram ABCD where BÂD = 64°
Elies on AB such that AÐE = 49°.
C С
D
49
Calculate
(i) ABC,
(ii) CỘE.
64
B
A
E

Answers
Answer:
m<ABC = 116°
m<CDE = 67°
Step-by-step explanation:
✔️m<ABC = 180 - m<BAD (adjacent angles of a parallelogram are supplementary)
m<ABC = 180 - 64° (Substitution)
m<ABC = 116°
✔️m<CDA = m<CDE + m<ADE (angle addition postulate)
m<CDA = m<CDE + 49°
m<CDA = m<ABC (opposite angles of a parallelogram are congruent)
m<CDE + 49° = 116° (substitution)
m<CDE = 116° - 49° (Substraction property of equality)
m<CDE = 67°
Solve these please!!!

Answers
The area of the figure ABDECA, and the coordinates of the points on the quadrilateral are;
1. The area is about 15.16 units²
2. The coordinates of the points are;
(i) B(5, 8)
(ii) C(8.58, 4)
(ii) D(8,58, 1.21)
What is a quadrilateral?A quadrilateral is a four sided polygon.
1. The coordinate of the point C can be found as follows;
Let (x, y) represent the coordinates of the C, we get;
(x + 8)/2 = 5
x = 2 × 5 - 8 = 2
(y + 8)/2 = 6
y = 2 × 6 - 8 = 4
The coordinates ot the point C (2, 4)
The length of the segment BC = √((8 - 2)² + (8 - 4)²) = 2·√(13)
Length of the side AB = √((8 - 6)² + (8 - 11)²) = √(4 + 9) = √(13)
The area of the triangle ABC = (1/2) × 2·√(13) × √(13) = 13
CE is perpendicular to DE, let (a, b), represent the coordinates of the point E, therefore;
(4 - y)/(2 - x) = -(5 - x)/(6 - y)
y - 4 = (-4/7)(x - 2)
y - 6 = (7/4)(x - 5)
(-4/7)(x - 2) + 4 = (7/4)(x - 5) + 6
x = (17/5) = 3.4
y = (7/4)((17/5) - 5) + 6 = 3.2
The coordinates of the point E is (3.4, 3.2)
The length of the side DE = √((5 - 3.4)² + (6 - 3.2)²) = √(10.4)
Length of the side CE = √((3.2 - 2)² + (3.4 - 4)²) = √(1.8)
Area of the triangle ΔCDE = (1/2) × √(10.4) × √(1.8)
Area of the figure is therefore;
13 + (1/2) × √(10.4) × √(1.8) ≈ 15.16 square units2. The equation of the line AB is; y - 6 = (1/3)·(x - (-1))
y - 6 = (1/3)·(x + 1)
y = (1/3)·(x + 1) + 6
The slope of the segment AE = (4 - 6)/(3 - (-1)) = -1/2
Slope of the segment BE = -1/(-1/2) = 2
Equation of BE is; y - 4 = 2·(x - 3)
y = 2·(x - 3) + 4 = (1/3)·(x + 1) + 6
Therefore, x = 5
y = (1/3)·(5 + 1) + 6 = 8
The coordinates of the point B is (5, 8)(ii) Area of the triangle EBC = 24 unit²
EB = (1/2) × √((5 - 3)² + (8 - 4)²) = √20
Therefore;
BC = 24/(√20) = 12/√5 = 12·√5/5 = √(28.8)
(x - 5)² + (y - 8)² = 28.8
y = 4, therefore;
(x - 5)² + (4 - 8)² = 28.8
(x - 5)² = 28.8 - (4 - 8)² = 12.8
x = √(12.8) + 5
The coordinates of the point C is C(√(12.8) + 5, 4) ≈ (8.58, 4)(iii) The equation of the segment AD is; y - 4 = (-1/2)(x - 3)
x = √(12.8) + 5
Therefore;
y - 4 = (-1/2)((√(12.8) + 5) - 3)
y = (-1/2)((√(12.8) + 5) - 3) + 4 ≈ 1.21
The coordinate of the pint D is about; D(8,58, 1.21)Learn more on parallel and perpendicular lines here: https://brainly.com/question/29526529
#SPJ1
For positive integer n, the factorial notation n! represents the product of the integers from n to 1. (For example, 6!= 6.5.4.3. 2. 1.) What value of N satisfies the following equation? 5!.9!= 12. N! (A)10 (B)11 (C)12 (D)13 (E)14
Answers
The value of N that satisfies the following equation, 5!9!= 12N!, is 10.
Factorial notation (n!) means to multiply a series of descending natural numbers. Also stated in the problem that for positive integer n, the factorial notation n! represents the product of the integers from n to 1.
Take for example 6! which can be written as 6 x 5 x 4 x 3 x 2 x 1 = 720.
Given the equation 5!9!= 12N!, expand the factorial notation.
(5 x 4 x 3 x 2 x 1)(9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1) = (4 x 3) N!
N! = (5 x 2 x 1)(9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1)
N! = 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
N = 10
Therefore, the value of N that satisfies the following equation, 5!9!= 12N!, is 10.
Learn more about factorial here: https://brainly.com/question/16868621
#SPJ4
PLEASE HELP ME THANKS!

Answers
Answer:
i think it is B. x^ab, but i could be wrong
Step-by-step explanation:
pemdas so take
x^(a+b)
x^(ab)
x^ab
probably wrong
Someone please help!!!!!

Answers
Where the friend made the error was in step 2. She should have squared the 4 first before multiplying by 2. The correct answer is 44
How to simplify mathematical expressions?We want to simplify the mathematical expression;
2(10 - 6)² + 3*4
The correct steps are as follows;
Step 1; Using BODMAS Acronym, let us deal with the bracket first to get;
2(4)² + 3*4
Step 2; Still dealing with the bracket, we will now have;
2(16) + 3*4
Step 3; Still dealing with the bracket, we will now have; 32 + 3*4
Step 4; Next sign to be used is multiplication sign and as such we now have; 32 + 12
Step 5; Using the addition sign, we now have 44
Thus, where the friend made the error was in step 2. She should have squared the 4 first before multiplying by 2.
Read more about Simplifying Mathematical Expressions at; https://brainly.com/question/723406
#SPJ1
Which statement is true about comparing 5.37 and 5.4?
5.4 is greater because 43
5.37 is greater because 7>4.
5.4 is greater because it has fewer digits.
5.37 is greater because it has more digits.
Answers
What is the next term in the pattern? 1,1,5,17,71,247
Answers
Answer: 1085
Step-by-step explanation:
Peter had 208 Canadian stamps and 186 Mexican stamps for sale. The stamps were mixed up and sold in packets of 6. How many packets of stamps were there? How many stamps were left over?
Answers
Answer:
65 packets and 4 stamps
Step-by-step explanation:
The first thing we see is that the stamps are mixed... which means they must be added.
208 + 186 = 394 stamps total
Now we see that each packet has 6 stamps. So we divide the number of stamps in total by 6.
394/6= 65.66667
Now we see from that number that the stamps can't quite make 66 packets, so there are 65 packets.
Now we find the number of stamps left over by multiplying the number of packets by 6.
65 x 6= 390
Now we take the total number of stamps minus the number of stamps in packets.
394 - 390 = 4
Therefore, there are four stamps left over.
Hope this helps!
If 18 pound of fertilizer covers 25 square feet of ground, how much fertilizer, in pounds, is needed to cover 1 square foot of ground?
Answers
Answer:
you need exactly 0.72 fertilizer but since its pounds, you round up so the answer is 1 pound.
Step-by-step explanation:
The amount of fertilizer required to cover 1 square foot of ground is 0.72
What is Proportion?
The proportion formula is used to depict if two ratios or fractions are equal. The proportion formula can be given as a: b::c : d = a/b = c/d where a and d are the extreme terms and b and c are the mean terms.
Given data ,
Amount of fertilizer required to cover 25 square foot ground = 18 pound
Amount of fertilizer required to cover 1 square foot ground = Amount of fertilizer required / total square foot ground
Amount of fertilizer required to cover 1 square foot ground = 18 / 25
Therefore , Amount of fertilizer = 0.72 pound
Hence , the amount of fertilizer required to cover 1 square foot of ground is 0.72
To learn more about proportion click :
https://brainly.com/question/27796974
#SPJ2
A study on the latest fad diet claimed that the amounts of weight lost by all people on this diet had a mean of 22.3 pounds and a standard deviation of 5.7 pounds. Step 2 of 2: If a sampling distribution is created using samples of the amounts of weight lost by 74 people on this diet, what would be the standard deviation of the sampling distribution of sample means
Answers
Answer:
The standard deviation of the sampling distribution of sample means would be of 0.6626 pounds.
Step-by-step explanation:
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
Standard deviation of 5.7 pounds.
This means that \(\sigma = 5.7\)
If a sampling distribution is created using samples of the amounts of weight lost by 74 people on this diet, what would be the standard deviation of the sampling distribution of sample means?
Sample of 74 means that \(n = 74\)
The standard deviaiton is:
\(s = \frac{\sigma}{\sqrt{n}} = \frac{5.7}{\sqrt{74}} = 0.6626\)
The standard deviation of the sampling distribution of sample means would be of 0.6626 pounds.
Are x = -4 and x = 6 solutions to 5x + 7 < 22?
TRUE OR FALSE
Answers
Answer:
x=-4 is true, x=6 is not
Step-by-step explanation:
5x + 7 < 22
Plug in our X values
5(-4) + 7 < 22 ?
solve
-20 + 7 < 22
-13 < 22 ?
x=-4 is true.
Repeat steps from ^
5(6) + 7 < 22
30 + 7 < 22
37 < 22 ?
x=6 is not true.
Hope this helped
Answer:
False
Step-by-step explanation:
5(-4) + 7 < 22
-20 + 7 < 22
-14 < 22
5(6) + 7 < 22
30 + 7 < 22
37 < 22
The statement would be false because when applying 6 to the equation, the equation becomes false.
On the other hand, when applying -4 to the equation, the equation becomes true, but since both -4 and 6 HAVE to be BOTH solutions to the equation, the statement becomes false.
In a clinical trial of a drug intended to help people stop smoking, subjects were treated with the drug for weeks, and subjects experienced abdominal pain. If someone claims that more than % of the drug's users experience abdominal pain, that claim is supported with a hypothesis test conducted with a significance level. Using as an alternative value of p, the power of the test is . Interpret this value of the power of the test.

Answers
The power of 0.95 shows that there is a 95% chance of rejecting the alternative hypothesis of p = 0.16 where the true proportion is actually 0.08. That is if the proportion of users who experience abdominal pain is actually 0.08, then there is a 8% chance of supporting the claim that the proportion of users who experience abdominal pain is more than 0.08.
How to Interpret the Power of a Hypothesis?Given that the alternative value of p is 0.16, it means that the power of the test is 0.95.
This means that if the true proportion of drug users experiencing abdominal pain is indeed 0.16, then by conducting the hypothesis test with a significance level of 0.05, we will correctly reject the null hypothesis and support the claim that more than 8% (0.08) of the drug's users experience abdominal pain with a probability of 0.95.
In other words, the power of 0.95 indicates that the test has a high chance (95%) of correctly detecting a true difference and correctly concluding that the proportion of drug users experiencing abdominal pain is greater than 8% when the true proportion is actually 16%. It demonstrates the test's ability to identify and support the alternative hypothesis when it is true.
It's important to note that the power of the test is influenced by factors such as sample size, significance level, effect size, and variability. In this case, with a power of 0.95, there is a high probability of detecting the claimed difference if it truly exists.
Read more about Power of Hypothesis at: https://brainly.com/question/32018073
#SPJ1
given that y= 4cm and O=52° work out x rounded to 1 dp right angle trigonometry
Answers
Answer:
4+52=56
\(y = 4cm and o = 52 work out x\)
56
Find the size of unknown angles

Answers
Step-by-step explanation:
2x+3x+x+20=180
6x+20=180
6x=160
x=160/6
x=26.667
Answer:
2X=53.2 , 3X=79.8 , X+20=46.6
Step-by-step explanation:
3X+2X+X+20=180
therefore,
6X+20=180
6X =180-20
6X =160
X = 160 over 6
X =26.6
now,
3X = 26.6 x3
=79.8
2X =26.6 x2
=53.20
X+20 =26.6+20
=46.6
Im not sure if it's right. Because the total does not make 180 degrees.