What is 12.18 x 103 =
Answers
Answer:
1,254.54
Step-by-step explanation:
Answer:
1,254.54
Step-by-step explanation:
Related Questions
Abbey Road Motors pays a percent commission to its sales people. They are paid
a percent of the profit the dealership makes on a car. If the profit is under $1,000,
the commission rate is 20%. If the profit is at least $1,000 and less than or equal to
$2,000, the commission rate is 20% of the first $1,000 and 24% of the remainder of
the profit. If the profit is above $2,000, the rate is 20% of the first $1,000 of profit,
24% of the next $1,000 of profit, and 29% of the amount of profit over $2,000. If p
represents the profit, express the commission c(p) algebraically as a split function.
Answers
Answer:
c(p) = {0.2 p ⇒ p < 1000
0.24 p - 40 ⇒ 1000 ≤ p ≤ 2000
0.29 p - 140 ⇒ p > 2000}
Step-by-step explanation:
* Lets explain how to solve the problem
- The profit is represented by p
1. If the profit is under $1,000, the commission rate is 20%
∵ The profit is p < 1000
∵ 20% of p = = 0.2 p
∵ c(p) is the function of the commission
∴ c(p) = 0.2 p when p < 1000
2. If the profit is at least $1,000 and less than or equal to $2,000, the
commission rate is 20% of the first $1,000 and 24% of the remainder
of the profit
- At least means greater than or equal
∵ The profit 1000 ≤ p ≤ 2000
- The commission is divided into 20% of first $1000 and 24% of
the reminder
∵ 20% of 1000 = = 200
∵ The remainder of the profit = p - 1000
∵ 24% of the remainder profit =
= 0.24(p - 1000) = 0.24 p - 240
∴ The total commission = 200 + 0.24 p - 240
∴ The total commission = 0.24 p - 40
∴ c(p) = 0.24 p - 40 when 1000 ≤ p ≤ 2000
3. If the profit is above $2,000, the rate is 20% of the first $1,000
of profit, 24% of the next $1,000 of profit, and 29% of the amount
of profit over $2,000
∵ The profit p > 2000
- The commission is divided into 20% of first $1000 and 24% of the
next $1,000 of profit, and 29% of the amount of profit over $2,000
∵ 20% of 1000 = = 200
∵ 24% of 1000 = = 240
- The amount of profit over $2,000 = p - 2000
∵ 29% of the amount of profit over $2,000 =
= 0.29(p - 2000)
= 0.29 p - 580
∴ The total commission = 200 + 240 + 0.29 p - 580
∴ The total commission = 0.29 p - 140
∴ c(p) = 0.29 p - 140 when p > 2000
* The commission function is:
c(p) = {0.2 p ⇒ p < 1000
0.24 p - 40 ⇒ 1000 ≤ p ≤ 2000
0.29 p - 140 ⇒ p > 2000}* Lets explain how to solve the problem
- The profit is represented by p
1. If the profit is under $1,000, the commission rate is 20%
∵ The profit is p < 1000
∵ 20% of p = = 0.2 p
∵ c(p) is the function of the commission
∴ c(p) = 0.2 p when p < 1000
2. If the profit is at least $1,000 and less than or equal to $2,000, the
commission rate is 20% of the first $1,000 and 24% of the remainder
of the profit
- At least means greater than or equal
∵ The profit 1000 ≤ p ≤ 2000
- The commission is divided into 20% of first $1000 and 24% of
the reminder
∵ 20% of 1000 = = 200
∵ The remainder of the profit = p - 1000
∵ 24% of the remainder profit =
= 0.24(p - 1000) = 0.24 p - 240
∴ The total commission = 200 + 0.24 p - 240
∴ The total commission = 0.24 p - 40
∴ c(p) = 0.24 p - 40 when 1000 ≤ p ≤ 2000
3. If the profit is above $2,000, the rate is 20% of the first $1,000
of profit, 24% of the next $1,000 of profit, and 29% of the amount
of profit over $2,000
∵ The profit p > 2000
- The commission is divided into 20% of first $1000 and 24% of the
next $1,000 of profit, and 29% of the amount of profit over $2,000
∵ 20% of 1000 = = 200
∵ 24% of 1000 = = 240
- The amount of profit over $2,000 = p - 2000
∵ 29% of the amount of profit over $2,000 =
= 0.29(p - 2000)
= 0.29 p - 580
∴ The total commission = 200 + 240 + 0.29 p - 580
∴ The total commission = 0.29 p - 140
∴ c(p) = 0.29 p - 140 when p > 2000
* The commission function is:
c(p) = {0.2 p ⇒ p < 1000
0.24 p - 40 ⇒ 1000 ≤ p ≤ 2000
0.29 p - 140 ⇒ p > 2000}
When a process is said to be at six sigma level, what does it
mean? (7 points)"
Answers
Answer:
Step-by-step explanation: It means a high level of quality, with 3.4 defects per million opportunities. It is this sigma level that leads to the term Six Sigma, which is a philosophy of delivering near perfect products or services by eliminating variabilities that lead to defects.
Jayesh records
the number of minutes he practices the
violin each day for a week. He wants to
know on which day he practiced the most
minutes. Should he draw a line plot or a line
graph? Explain.
Answers
A line plot would be more appropriate for Jayesh's situation
What is plots?A plot refers to a graphical representation of data or mathematical functions. The most common types of plots include scatter plots, line plots, bar graphs, histograms, and pie charts. Scatter plots are used to show the relationship between two variables, while line plots and bar graphs are used to display categorical or numerical data. Histograms show the distribution of numerical data, and pie charts show the proportion of different categories in a whole.
According to the given information:
Jayesh should draw a line plot to determine on which day he practiced the most minutes. A line plot, also known as a dot plot, is a simple and effective way to display small sets of data. It shows the frequency of each value in a data set by placing a dot above the corresponding value on a number line. In Jayesh's case, he can use a line plot to record the number of minutes he practices the violin each day for a week, and then identify the day on which he practiced the most minutes by simply looking for the highest dot on the plot.
On the other hand, a line graph is used to display trends or patterns in data over time or other continuous variables. It connects data points with straight lines, and is best used when there is a large set of data points or when the data is continuous. Therefore, a line plot would be more appropriate for Jayesh's situation since he is only tracking the minutes practiced each day, and not looking for a trend over time.
To know more about Plot visit :
https://brainly.com/question/29573088
#SPJ1
a radioactive substance decays exponentially. a scientist begins with 180 milligrams of a radioactive substance. after 33 hours, 90 mg of the substance remains. how many milligrams will remain after 43 hours?
Answers
The required weight after 43 hours is 72. 96mg
How to determine the valueFrom the information given, we have that;
A Scientist begins with 180 milligrams of a radioactive substance
Let us take Po = 180 milligrams
Using the expression;
\(P(t) = Poe^k^t\)
Substituting the values of t = 33, P = 90mg and Po = 180
90 = 180e^33t
\(e^3^3^t = \frac{1}{2}\)
Take the log of both sides
\(33ln(e^k) = ln (\frac{1}{2} )\)
\(k = -\frac{ln 2}{33}\)
k = - 0. 0210
The equation becomes: P(t) = 150e^-0.0210
Substitute t as 43
\(P(43) = 180e^-^0^.^0^2^1^0 ^*^4^3\)
P(43) = 72. 96 mg
Hence, 72. 96 mg will remain after 43 hours.
Learn more about radioactive decay here:
https://brainly.com/question/11117468
#SPJ4
May I please have the correct answer please? I will give you whatever you want

Answers
= 1/4^3
=1/4x4x4
=1/64
What's X?
Thank youuu

Answers
Answer:
35°
Step-by-step explanation:
Please see the attached picture for full solution.

Jeremy likes to paint. He estimates the number of paintings he completes using the function P of w equals one third times w plus four, where w is the number of weeks he spends painting. The function J(y) represents how many weeks per year he spends painting. Which composite function would represent how many paintings Jeremy completes in a year
Answers
Therefore , the solution of the given problem of function comes out to be it is compatible with P(J(y)) = 1/3J(y) +4.
What is meant by the word function?Math is a science that studies numbers, their variants, math and the tissues in the area, shapes, and both their real and possible locations. 'Function' refers to the relationship between a set of inputs, which each have a corresponding output. A function is a relationship between inputs in which each input yields a single variable, distinct output.
Here,
Given:
The quantity of paintings is returned by the function P, which accepts a number of months as an argument.
The function J returns the number of weeks in a year after accepting an undefined parameter.
P(weeks annually) = P(J(y)) seems to be the composites function that will provide the annual number of paintings.
Choice C is compatible with P(J(y)) = 1/3J(y) +4.
Therefore , the solution of the given problem of function comes out to be it is compatible with P(J(y)) = 1/3J(y) +4.
To know more about function visit:
https://brainly.com/question/28193995
#SPJ4
it takes carlos 9 minutes to drive from home to work at an average rate of 22 miles per hour. how many minutes will it take carlos to cycle from home to work along the same route at an average rate of 6 miles per hour?
Answers
It will take Carlos 33 minutes to cycle from home to work along the same route at an average distance rate of 6 miles per hour.
To find out how many minutes it will take Carlos to cycle from home to work, we'll need to determine the distance of the route first, and then calculate the time it takes to cover that distance at the average cycling speed.
To solve this problem, we can use the formula:
time = distance/speed
1. Find the distance: Since Carlos drives from home to work in 9 minutes at an average rate of 22 miles per hour, we can calculate the distance using the formula: distance = rate × time.
First, convert the time from minutes to hours: 9 minutes ÷ 60 minutes/hour = 0.15 hours.
Now, calculate the distance: distance = 22 miles/hour × 0.15 hours = 3.3 miles.
2. Calculate the cycling time: Now that we know the distance is 3.3 miles, we can find out how long it will take Carlos to cycle at an average rate of 6 miles per hour.
Use the formula: time = distance ÷ rate.
time = 3.3 miles ÷ 6 miles/hour = 0.55 hours.
Now, convert the time back to minutes: 0.55 hours × 60 minutes/hour = 33 minutes.
So, it will take Carlos 33 minutes to cycle from home to work along the same route at an average rate of 6 miles per hour.
Learn more about distance:
brainly.com/question/15172156
#SPJ11
What is the average rate of change of f(x) = −x2 + 3x + 6 over the interval −3 ≤ x ≤ 3? A. −2 B. −1 C. 3 D. 6
Answers
A function is a relation between a set of inputs and a set of possible outputs, where each input is uniquely associated with a single output.the average rate of change of f(x) over the interval \([-3, 3]\) is:
\((6 - (-12)) / 6 = 18/6 = 3\) Thus, option C is correct.
What is the average rate of change of f(x)?The average rate of change of a function over an interval is given by the difference in the function values at the endpoints of the interval, divided by the length of the interval.
Therefore, to find the average rate of change of \(f(x) = − + 3x + 6\) over the interval \(−3 ≤ x ≤ 3\), we need to evaluate the function at the endpoints of the interval and then divide by the length of the interval.
\(f(-3) = + 3(-3) + 6 = -9 - 9 + 6 = -12\)
\(f(3) = + 3(3) + 6 = -9 + 9 + 6 = 6\)
The length of the interval is 3 - (-3) = 6.
Therefore, the average rate of change of f(x) over the interval \([-3, 3]\) is:
\((6 - (-12)) / 6 = 18/6 = 3\)
Learn more about function here:
brainly.com/question/12431044
#SPJ1
i need help with these


Answers
V = area of cross-section x length
= (7x3) x 2
= 42 unit^3
Q to R - cosine rule comes to mind
PQ is 8mm (radius along with PR)
QR = the square root of:
8^2 + 8^2 - 2 x 8 x 8 x cos120 = 8root 3
Or 13.8564....
(root means square root)
Thus, QR = 13.86mm
A = 120/360 x 3.14 x 8 x 8
= 66.9866....
Area of sector is 67 to the nearest mm^2
Hope this helps!
Multiply
-3.7
A. -21
B. -11
C. 21
D. 11
Answers
Answer:
A
Step-by-step explanation:
negative times a postive is always negative unless squared
Answer:
A. -21
Step-by-step explanation:
Note that when you multiply a negative with a positive number, your answer will be negative. Multiply as usual:
-3 * 7 = -21
A. -21 is your answer.
~
if a positive association exists between two quantitative variables, the slope will be negative the slope will be 0. the slope will be positive we do not know if the slope will be positive or negative
Answers
If a positive association exists between two quantitative variables, the slope will be positive.
Why the slope will be positive?
A quantitative variable is a variable that takes on numerical values that are either counted or measured. The weight of a newborn baby, the height of a tree, the number of questions answered correctly on a quiz, and the number of students in a classroom are all examples of quantitative variables.
A positive association exists when two variables increase in tandem with one another. When one variable increases, the other variable also increases. Alternatively, when one variable decreases, the other variable also decreases.
A linear relationship between two variables is defined by the slope of the line connecting them. The slope of the line can be found by calculating the change in y (the dependent variable) divided by the change in x (the independent variable).The slope of a line will be positive if there is a positive association between two quantitative variables. A negative association will be indicated by a negative slope. If there is no association, the slope will be zero, and if it cannot be determined, we will not know if the slope will be positive or negative.
Learn more about Quantitative Variable.
brainly.com/question/30366950
#SPJ11
solve for x please hurry i will mark brainiest when it shows up if you answer correctly

Answers
The value of missing length x in the congruent triangles is determined as 3.6.
option D.
What is the length of segment of x?The length of segment x is calculated by applying congruency theorem as follows;
Consider triangle ABC,
AQ/AT = AB / AC
The given parameters include;
length AQ = 5
length AT = 6
length AB = 5 + 3 = 8
length AC = 6 + x
The value of missing length x is calculated as follows;
5/6 = 8/(6 + x )
5(6 + x) = 6(8)
30 + 5x = 48
5x = 48 - 30
5x = 18
x = 18/5
x = 3.6
Learn more about congruent lines here: https://brainly.com/question/30295250
#SPJ1
According to the nutrition facts for these potato chips, a serving has 170
mg of sodium, or 7% of the daily recommended value for an average adult.
Based on this information, how many milligrams of sodium should an
average adult consume in a day?
O2428.57 or about 2400 mg
2 1500 mg
amin B6 10%
247.2 or about 300 mg
Answers
Answer:
2428.57mg
Step-by-step explanation:
170 mg of sodium =7%
170/7% = 2428.57mg
HELP!! I NEED HELP WITH MY MATH

Answers
Answer:
partA option B is the correct answer
partB option A is the correct answer
on the 1st of January a student puts N10 in a box. on the 2nd she puts N20 in the box. putting the same number of 10 naira notes as the day of the month. how much money will be in the box if she keeps doing this for the first 10 days of January and the whole of January
Answers
Answer:
N550
N4960
Step-by-step explanation:
10 days
First day: N10
Second day: N20
Third day: N30
...
Tenth day: N100
Sum of sequence: 10 + 20 + 30 + 40 + ... + 80 + 90 + 100
sum = (n/2)[2a+(n−1)d]
a = 10; n = 10; d = 10
sum = (10/2) × [2(10) + (10 - 1)(10)]
sum = 5[20 + 9(10)]
sum = 5[110]
sum = 550
Answer: N550
31 days
First day: N10
Second day: N20
Third day: N30
...
Thirty-first day: N100
Sum of sequence: 10 + 20 + 30 + 40 + ... + 290 + 300 + 310
sum = (n/2)[2a+(n−1)d]
a = 10; n = 31; d = 10
sum = (31/2) × [2(10) + (31 - 1)(10)]
sum = 15.5[20 + 30(10)]
sum = 15.5[320]
sum = 4960
Answer: N4960
Solve the system of linear equations using elimination.
-5x + 3y = -19
-x – 3y = -11
Answers
What the first person said
How many significant figures are in 0.0624000?
Answers
Answer:
Use notes and youll get an answer
Step-by-step explanation:
(6-4x+2u)(-8) use distributive property to remove parenthesis
Answers
Answer:
-16u+32x−48
Step-by-step explanation:
(6-4x+2u)(-8)
Rearrange terms.
(2u-4x+6)(-8)
Re-order terms so constants are on the left.
-8(2u-4x+6)
Distribute.
-16u+32x−48
Hope this helps :)
A police car drives for 11/12 hours with a constant speed of 84 mph and then for another 2 hours 15 minutes with a constant speed of 72 mph. What distance did it go?
Answers
Answer:
1170 miles
Step-by-step explanation:
multiply 12 x 84 to get 1008 keep that 1008 for later. divide 72 by 60 you should get 1.2, times 1.2 and 15 and you should get 18 keep the 18. times 2 by 72 and get 144. add 144 and 18 to get 162. add 162 and 10008 to get 1170. the awnser is 1170 miles.
suppose that for some hypothesis test on the mean of a normally distributed population, standard deviation known, the p-value is computed as 0.11. if a level of significance of 0.05 is used, is rejecting the null hypothesis in favor of the alternative the correct decision?
Answers
If the p-value for a hypothesis test is greater than the chosen level of significance, then the null hypothesis cannot be rejected.
In this case, the p-value is 0.11 and the level of significance is 0.05. Since the p-value is greater than the level of significance, we cannot reject the null hypothesis.
Therefore, we do not have sufficient evidence to conclude that the population mean is different from the hypothesized value. In other words, we do not have enough evidence to support the alternative hypothesis.
Thus, rejecting the null hypothesis in favor of the alternative hypothesis is not the correct decision in this case.
Learn more about hypothesis test, here:
brainly.com/question/14587073
#SPJ11
Think About a Plan Triangle A B C is a right triangle with right angle C . Show that cos ² B/2=a+c/2 c
b. How can you find the ratio or ratios you need to substitute in the identity?
Answers
To show that cos²(B/2) = (a + c)/(2c), we can use the identities involving the sides of a right triangle and trigonometric functions.
In a right triangle ABC with right angle C, we can relate the sides using the Pythagorean theorem and trigonometric functions. Let's consider the following ratios:
sin(B) = a/c,
cos(B) = b/c.
We can express sin(B) in terms of cos(B/2) using the half-angle identity:
sin(B) = 2sin(B/2)cos(B/2).
Squaring both sides of the equation gives:
sin²(B) = 4sin²(B/2)cos²(B/2).
Next, we can express sin²(B) using the Pythagorean identity:
sin²(B) = 1 - cos²(B).
Substituting this into the equation gives:
1 - cos²(B) = 4sin²(B/2)cos²(B/2).
Rearranging the equation, we have:
cos²(B/2) = (1 - cos²(B))/(4sin²(B/2)).
Using the ratio sin(B) = a/c, we can substitute sin²(B/2) = (a/c)²/2, which simplifies to a²/(2c²).
Similarly, using cos(B) = b/c, we can substitute cos²(B) = (b/c)².
Substituting these ratios in the equation, we obtain:
cos²(B/2) = (1 - (b/c)²)/(4(a²/(2c²))),
= (c² - b²)/(8a²).
Simplifying further, we get:
cos²(B/2) = (a² + c² - b²)/(8a²),
= (a + c)/(2c).
Therefore, we have shown that cos²(B/2) = (a + c)/(2c).
Learn more about right triangle here:
https://brainly.com/question/29285631
#SPJ11
5) Using the definition, prove that in a metric space \( (X, d) \), \( A \subseteq X \quad A \) is open if and only if \( A^{c} \) is closed.
Answers
Combining both directions of the proof, we have shown that in a metric space ((X, d)), (A \subseteq X) is open if and only if (A^c) is closed.
To prove that in a metric space ((X, d)), (A \subseteq X) is open if and only if (A^c) is closed, we need to show both directions of the implication:
If (A) is open, then (A^c) is closed.
If (A^c) is closed, then (A) is open.
Let's start with the first direction:
If (A) is open, then (A^c) is closed:
Assume (A) is open. To prove that (A^c) is closed, we need to show that its complement, ((A^c)^c = A), is open.
Since (A) is open, for every point (x \in A), there exists a neighborhood around (x) that is fully contained within (A). In other words, for each (x \in A), there exists an open ball (B(x, r_x)) such that (B(x, r_x) \subseteq A).
Now, consider any point (y \in A^c). We want to show that there exists a neighborhood around (y) that is fully contained within (A^c).
Let's define (r_y) as the smallest radius among all the open balls centered at points in (A) (i.e., (r_y = \min{r_x : x \in A})). Since (A) is open, (r_y > 0) because each (B(x, r_x)) fully lies in (A), and therefore no point on the boundary of (A) can be contained in any (B(x, r_x)).
Now, consider the open ball (B(y, r_y/2)) centered at (y) with a radius of (r_y/2). We claim that this open ball is fully contained within (A^c).
To prove this, consider any point (z) in (B(y, r_y/2)). By the definition of the open ball, we have (d(z, y) < r_y/2). Now, since (r_y) is the smallest radius among all open balls centered at points in (A), it follows that (d(z,x) \geq r_y/2) for all (x \in A). Thus, (z) cannot be in (A) and must be in (A^c).
Therefore, we have shown that for every point (y \in A^c), there exists an open ball (B(y, r_y/2)) fully contained within (A^c). This implies that (A^c) is open, and hence, the complement of (A^c), which is (A), is closed.
Now let's move to the second direction:
If (A^c) is closed, then (A) is open:
Assume (A^c) is closed. To prove that (A) is open, we need to show that for every point (x \in A), there exists a neighborhood around (x) that is fully contained within (A).
Consider any point (x \in A). Since (x \notin A^c), it follows that (x) is in the interior of (A^c) (because if (x) were on the boundary or exterior of (A^c), it would be in the closure of (A^c) and thus not in the interior).
As (x) is in the interior of (A^c), there exists an open ball (B(x, r)) centered at (x) such that (B(x, r) \subseteq A^c).
That means every point (y) within the open ball (B(x, r)) is in (A^c), implying that (y) is not in (A). Therefore, (B(x, r)) is fully contained within (A).
Hence, for every point (x \in A), there exists an open ball (B(x, r)) fully contained within (A), which proves that (A) is open.
learn more about metric space here
https://brainly.com/question/33724940
#SPJ11
assume that you want to construct a value weighted index using these securities and that you want the initial value of your index to be 100 billion. what should be the devisor?
Answers
Answer: 1735259
Step-by-step explanation:
I think I did this before.
The Divisor is 100 billion / M.
A value-weighted index is a stock market index in which stocks are weighted according to the market capitalization of the corporation. To answer the given question, we need to understand what a value-weighted index is and what divisor to be considered to get an initial value of 100 billion.
A value-weighted index is a stock market index in which stocks are weighted according to the market capitalization of the corporation. Large corporations have a greater influence on the index’s value than small corporations. The index is computed by dividing the total market value of the stocks in the index by a divisor to arrive at an index value. The divisor is constantly changing since changes in market value alter it.
The devisor is calculated by dividing the initial value of the index by the sum of the market capitalizations of the stocks in the index, that is,If V is the initial value of the index andM1, M2, ……, Mn are the market capitalizations of the n stocks in the index, then the divisor D is given by:
D=V / (M1 + M2 + ... + Mn)
For the given problem, the divisor can be computed as follows:
Assuming the total market value of stocks to be M,
where, V = 100 billion.
Then,
Divisor = 100 billion / M.
To learn more about the value-weighted index refer to:
https://brainly.com/question/30745513
#SPJ11
Bret buys a dining table that costs $150 before tax. The sales tax is 8%. How much sales tax did he pay?
Answers
Answer:
$12
Step-by-step explanation:
to find sales tax you multiply the cost by the percentage
you do 150 * 8%
thats also 150 * 0.08
150 * 0.08 is 12
so you pay $12 in tax
Bret paid $12 as sales tax.
What is a expression? What is a mathematical equation? What is Equation Modelling? What is denominator?A mathematical expression is made up of terms (constants and variables) separated by mathematical operators. A mathematical equation is used to equate two expressions. Equation modelling is the process of writing a mathematical verbal expression in the form of a mathematical expression for correct analysis, observations and results of the given problem. In a fraction say (x/y), [y] is called denominator.
We have Bret buys a dining table that costs $150 before tax. The sales tax is 8%.
Assume that he paid $[x] as sales tax. Then, we can write -
[x] = 8% of 150
[x] = (8/100) x 150
[x] = 12
Therefore, Bret paid $12 as sales tax.
To solve more questions on Equations, Equation Modelling and Expressions visit the link below -
brainly.com/question/14441381
#SPJ2
What is the value of w in this equation?
15 + w = 75
Answers
Answer:
\(w=60\)
Step-by-step explanation:
\(15+w=75\)
Subtract 15 from both sides of the equation.
\(15+w-15=75-15\)
\(w=60\)
Answer:W=60
Step-by-step explanation:
Simplify both sides of the equation.
W+15=75
Then Subtract 15 from both sides.
W+15-15=75-15
15-15=0 leaving w on its own. 75-15=60
W=60
A fitness center is interested in finding a 90% confidence interval for the mean number of days per week that Americans who are members of a fitness club go to their fitness center. Records of 257 members were looked at and their mean number of visits per week was 2.6 and the standard deviation was 1.3. Round answers to 3 decimal places where possible. a. (1 pt) Fill in the blank: To compute the confidence interval use a distribution. b. (6 pts) With 90% confidence the population mean number of visits per week is between and visits. c. (1 pt) If many groups of 257 randomly selected members are studied, then a different confidence interval would be produced from each group. About percent of these confidence intervals will contain the true population mean number of visits per week and about percent will not contain the true population mean number of visits per week.
Answers
A fitness center is interested in finding a 90% confidence interval for the mean number of visits per week that Americans who are members of a fitness club go to their fitness center, a distribution is used.
To compute a confidence interval, a distribution is used. In this case, since the sample size is large (257 members), the distribution used is the standard normal distribution. The formula to calculate the confidence interval is:
Confidence Interval = sample mean ± (critical value) * (standard deviation / √n)
The critical value is determined based on the desired level of confidence. For a 90% confidence level, the critical value corresponds to the 5th percentile and the 95th percentile of the standard normal distribution.
Using the given information, the sample mean is 2.6, the standard deviation is 1.3, and the sample size is 257. Plugging these values into the formula, we can calculate the lower and upper bounds of the confidence interval.
The resulting confidence interval will provide an estimate of the range within which the true population mean number of visits per week is likely to fall, with 90% confidence.
If many groups of 257 randomly selected members are studied, each group will produce a different confidence interval. The true population mean number of visits per week will be contained within a certain percentage of these intervals, which is determined by the chosen confidence level (90% in this case). The remaining percentage of intervals will not contain the true population mean. The exact percentages can be calculated based on the properties of confidence intervals and the concept of coverage probability.
Learn more about mean here:
https://brainly.com/question/31101410
#SPJ11
Please help!!! thank you!!! *will give brainliest*
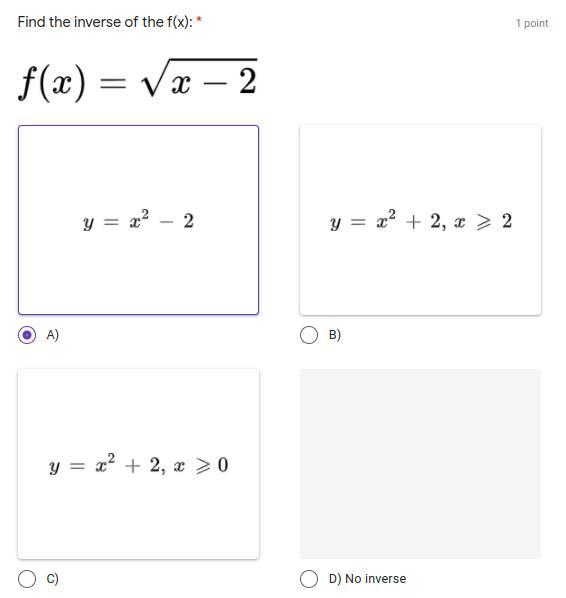
Answers
Answer: Choice C
\(y = x^2+2, \ x \ge 0\)
=============================================
Work Shown:
\(f(x) = \sqrt{x-2}\\\\y = \sqrt{x-2}\\\\x = \sqrt{y-2} \ \text{ swap x and y}\\\\x^2 = y-2 \ \text{ square both sides}\\\\y = x^2+2\\\\f^{-1}(x) = x^2+2\\\\\)
Since the range of f(x) is \(y \ge 0\) this means the domain of the inverse will be \(x \ge 0\)
The domain and range swap when you go from the original function to the inverse, or vice versa (due to x and y swapping)
So we must state the inverse is \(y = x^2+2 , \ x \ge 0\)
Consider this equation.
cos(θ) = 4sqrt41/41
If θ is an angle in quadrant IV, what is the value of sin(θ) ?

Answers
Answer:
A. -5√41/41Step-by-step explanation:
Let the horizontal leg = 4√41 and the hypotenuse = 41 as
cosine = adjacent leg / hypotenuse.Then the vertical leg is:
√(41² - 16*41) = √25*41 = 5√41Since the vertical leg is below the x-axis, its value is -5√41
Then we have:
sin (θ) = -5√41/41Correct choice is A
Answer:
Step-by-step explanation: i just take the test

please help me out here :’(

Answers
Answer:
Step-by-step explanation:
We are going to use the areas given to find the lengths of the sides of each of their respective squares. For the purple square, the area is 35 units squared. Because the formula for the area is A = s * s, then we can fill in the value for the area and solve for s, the side length, of the purple square.
\(35=s^2\) and
\(s=\sqrt{35}\). That side length also serves as the height of the right triangle. Now on to the blue square on the bottom. It has an area of 50 units squared, so
\(50=s^2\) and
\(s=\sqrt{50}\). We could feasibly simplify that, but it's not necessary, really. That side serves as the base of the right triangle. Now we can use Pythagorean's Theorem to find the length of the hypotenuse of the right triangle, which also serves as the side of the big blue square. We will call the side of the big blue square x.
\(x^2=(\sqrt{35})^2+(\sqrt{50})^2\) and
\(x^2=35+50\) and
\(x^2=85\) and
\(x=\sqrt{85}\). That is the side length of the large blue square. The area for the square is s * s, and since we know the side length to be √85:
\(A=(\sqrt{85})(\sqrt{85})\) so
A = 85 units squared