What are the two modes? What mode does your calculator need to be set on? How do you change the mode?
Answers
Related Questions
When x = 4, what is 6x – 18?
Answers
Hey there!☺
\(Answer:\boxed{6}\)
\(Explanation:\)
If x is equal to 4, then you will have to multiply 6 by x which is 4.
\(6*4=24\)
Now subtract 18 from 24.
\(24-18=6\)
\(6x-18=6\)
6 is your answer.
Hope this helps!☺
the diffrence of 54 and 32 mutlipted by the diffrence of 8 and 5
Answers
Answer:
66
Step-by-step explanation:
the difference of 54 and 32 is 54 - 32 = 22
the difference of 8 and 5 is 8 - 5 = 3
then
22 × 3 = 66
Given the following definitions: U = {1, 2, 3, 4, 5, 6, 7} A = {1, 2, 4, 5} B = {1, 3, 5, 7} How many elements are in A ∩ B' ?
Answers
Only 1 and 5
If f(x) =\(\sqrt{x} +3\) , what is the equation for f–1(x)?
Answers
Answer: \(f^{-1}(x) = (x-3)^2\)
Step-by-step explanation:
We are given that \(f(x) = \sqrt{x} + 3\). A trick to solve for the inverse is to switch the f(x) and x in the equation. This gives us
\(x = \sqrt{f(x)} + 3\)
Now, we can solve for this f(x) which gives us
\(x = \sqrt{f(x)} + 3\\x -3 = \sqrt{f(x)}\\(x -3)^2 = f(x)\)
Then we simply let that \(f(x)\) be \(f^{-1}(x)\). Thus, we have \(f^{-1}(x) = (x-3)^2\)
What makes a zero? Using zero to simplify algebraic expressions

Answers
It should be noted that an algebraic expression will be equal to zero when the difference is between the same expressions.
How to illustrate the information?It should be noted that an algebraic expression simply means the expression that's used to show the relationship between the variables
In this case, the should be noted that an algebraic expression will be equal to zero when the difference is between the same expressions.
An example is illustrated as:
= 2x - 2x
= 0
Learn more about algebra on:
brainly.com/question/22399890
#SPJ1
Please help
will mark BRAINLIEST

Answers
The angle sum property of a triangle and the angle formed between a tangent and a radius of a circle indicates.
m∠ADC = 58°
What is a tangent to a circle?A tangent to a circle is a straight line which touches the circumference of a circle at only one point.
The vertical angles theorem indicates that we get;
∠1 ≅ ∠2
Therefore; m∠1 = m∠2
The tangent to a circle indicates that we get;
The angle formed at vertex B and Q are 90 degrees angles and the triangles ABP and AQP are right triangles, which indicates that the acute angles of each of the right triangles are complementary, therefore;
m∠1 + 26° = 90°
m∠1 = 90° - 26° = 64°
Therefore, m∠2 = m∠1 = 64°
m∠2 = m∠CAD = 64°
The segments AC and AD are radial lengths therefore, the triangle ΔACD is an isosceles triangle.
m∠ADC ≅ m∠ACD (Base angles of an isosceles triangle)
The angles ∠ADC and ∠ACD are therefore;
m∠CAD + m∠ADC + m∠ACD = 180° (Angle sum property of a triangle)
m∠CAD + m∠ADC + m∠ADC = 180°
m∠CAD + 2 × m∠ADC = 180°
64° + 2 × m∠ADC = 180°
m∠ADC = (180° - 64°)/2 = 58°
m∠ADC = 58°
Learn more on the angle sum property of a triangle here: https://brainly.com/question/22262639
#SPJ1
Does anyone know this answer??

Answers
Answer:
96.25%
Step-by-step explanation:
The empirical rule regarding mean and standard deviation is that
Around 68% of scores are between 40 and 60.Around 95% of scores are between 30 and 70.Around 99.7% of scores are between 20 and 80.Therefore between mean and +2 standard deviation or between mean and -2 standard deviation you will find approximately 95/2 = 47.5% of the values
Between mean and ± 3 standard deviations you will find approximately 97.5/2 = 48.75% of the values
Therefore between 2 standard deviations above and 3 standard deviations below you will find approximately 47.5 + 48.75 = 96.25% of values
ANSWER PLEASE! ITS HARD!!Graph the image of triangleXYZ after a dilation with a scale factor of
1
4
and the origin as its center. Then enter an algebraic rule to describe the dilation. Express any fractions in the rule for the dilation in simplest form.



Answers
Relax this isn't really that hard. We're given a triangle with coordinates
X(4,4), Y(12,12), Z(4,12)
and we're told to dilate it around the origin by scale factor 1/4. The origin part makes it easy; this just means we multiply all the coordinates by 1/4.
So our new triangle is
X'(1,1), Y'(3,3), Z'(1,3)
which we plot in red.
Is that third page asking for the lengths? We have
X'Y' is the hypotenuse of a right triangle with legs 2 and 2, so
|X'Y'| = 2√2
|Y'Z'| is 3-1 = 2
|Z'X'| = 2
The rule is
(x,y) → (x/4, y/4)
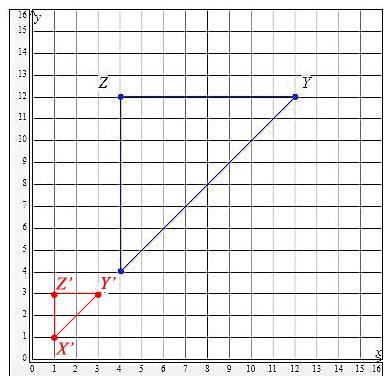
Scale factors are used to enlarge or reduce the size of a shape
The coordinates of the dilated triangle are (1,1), (3,3) and (1,3)
The coordinates of the triangle are given as:
\(X = (4,4)\)
\(Y = (12,12)\)
\( Z = (4,12)\)
The scale factor of dilation is given as:
\(k=\frac 14\)
The coordinates of the new triangle after dilation are calculated as follows:
\(X' = (4,4) \times \frac 14\)
\(X' = (1,1)\)
\(Y' = (12,12) \times \frac 14\)
\(Y' = (3,3)\)
\(Z' = (4,12) \times \frac 14\)
\(Z' = (1,3)\)
So, the dilation rule is:
\((x,y) \to \frac 14(x,y)\)
Hence, the coordinates of the dilated triangle are (1,1), (3,3) and (1,3)
See attachment for the image of the triangle
Read more about dilations at:
https://brainly.com/question/10253650

The volume of a cone is 13.4m cubed and the radius is 3.2m what is the height
Answers
Answer:
The height is 1.25m.
Step-by-step explanation:
Volume = 1/3 πr²h
Given:
V = 13.4 m³
r = 3.2 m
Asked: height (h)
Substitute the formula with the given values then solve
13.4m³ = 1/3π(3.2m)²h
13.4(3) = 10.24πh
40.2 = 10.24πh
h = 40.2/10.24π
h = 1.25m
The height of the cone is 1.25 meters.
We know that the volume of the cone is given by
V = (1 / 3) * π * r ^2 * h................equation 1
where,
V is the volume of the cone.
r is the radius of the cone's base
h is the height
The volume and radius of the cone are given,
V = 13.4 m
r = 3.2m
substituting these values in equation 1 we get,
13.4 = (1 / 3) * 3.14 * 3.2 ^ 2 * h
on simplifying further
13.4 = 10.717 * h
h = 1.25m
The height of the cone is 1.25 meters.
Learn more about the total Surface Area of the Cone :
https://brainly.com/question/15153049
5.275 to 2 decimal places
Answers
Answer:
5.29
..................................
Tina pet sits to earn extra money. She charges a flat service fee of $20, plus $15 per day. If one of her customers spent less than $125, which of the following inequalities could be used to solve for x, the number of days the customer paid for pet sitting?
Answers
Therefore, **x < 7** is the inequality that may be utilized to find x
What is inequality?A mathematical statement known as an inequality compares two expressions using an inequality sign, such as (less than), > (greater than), or (less than or equal to).
For instance, the inequality x + 2 5 signifies that "x + 2 is less than 5".
Let x represent how many days the client paid for pet sitting.
$15 per day plus a $20 fixed service fee equals the total cost of pet sitting.
We are aware that the customer's purchase was under $125. Consequently, we can write:
20 + 15x < 125
Putting this disparity simply:
15x < 105
x < 7
To know more about inequality visit:
brainly.com/question/11536194
#SPJ1
The weight of oranges growing in an orchard is normally distributed with a mean
weight of 5.5 oz. and a standard deviation of 1.5 oz. Using the empirical rule,
determine what interval would represent weights of the middle 95% of all oranges
from this orchard.
Answers
Answer:
5.5-1.5= 4.
4*0.95= 3.8
so the mid weight is 3.8oz.
6x^2=-3x+1 to the nearest hundredth
Answers
The solutions to the quadratic equation 6x² = -3x + 1 to the nearest hundredth are -0.73 and 0.23.
What are the solutions to the quadratic equation?Given the quadratic equation in the question:
6x² = -3x + 1
To solve the quadratic equation 6x² = -3x + 1, we can rearrange it into standard form, where one side is set to zero:
6x² + 3x - 1 = 0
Now we can solve the equation using the quadratic formula, which states that for an equation in the form ax² + bx + c = 0, the solutions for x are given by:
\(x = \frac{-b \±\sqrt{b^2-4ac} }{2a}\)
Here; a = 6, b = 3, and c = -1.
Let's substitute these values into the quadratic formula:
\(x = \frac{-b \±\sqrt{b^2-4ac} }{2a}\\\\ x= \frac{-3 \±\sqrt{3^2-4\ *\ 6\ *\ -1} }{2*6}\\\\x = \frac{-3 \±\sqrt{9+24} }{12}\\\\x = \frac{-3 \±\sqrt{33} }{12}\\\\x = -0.73, \ x=0.23\)
Therefore, the values of x are -0.73 and 0.23.
Learn more about quadratic equations here: brainly.com/question/1863222
#SPJ1
The two top concert tours in 2016 were concert A and concert B. Based on average ticket prices, it cost a total of $1707 to purchase six tickets for concert A and six tickets for concert B. Three tickets for concert B cost a total of $687. How much did an average ticket cost for each tour?
Answers
The average ticket cost for each concert is given as follows:
Concert A: $188.83.Concert B: $95.67.How to obtain the ticket costs?The ticket costs are obtained by a system of equations, for which the variables are given as follows:
Variable a: cost for Concert A.Variable b: cost for Concert B.It cost a total of $1707 to purchase six tickets for concert A and six tickets for concert B, hence:
6a + 6b = 1707
a + b = 284.5.
Three tickets for concert B cost a total of $687, hence the cost for concert B is of:
3b = 687
b = 287/3
b = $95.67.
Replacing into the first equation, the cost for concert A is given as follows;
a = 284.5 - 95.67
a = $188.83.
More can be learned about a system of equations at https://brainly.com/question/30374328
#SPJ1
.54 oz of premium walnuts costs $12.95. what is cost per ounce
Answers
The cost per ounce of the premium walnut is $0. 23
What is proportion?To determine the value of the cost, we need to note that proportion is simply described as the comparison of numbers such that they are made equal to another.
From the information given, we have that;
54 ounces of premium walnuts costs $12.95
This is represented as;
54 ounces = $12. 95
Then 1 = x
cross multiply the values, we get;
x = $12.95/54
Divide the values, we get;
x = $0. 23
Hence, the value is $0. 23 per premium walnut
Learn more about proportion at: https://brainly.com/question/1781657
#SPJ1
Peterson Packaging Inc. does not currently pay dividends. The company will start with a $0.70 dividend at the end of year three and grow it by 10% for each of the next six years. After six years of growth, it will fix its dividend at $1.36 forever. If you want a 15% return on this stock, what should you pay today given this future dividend stream?
Answers
solve for x
(look at photo)

Answers
By definition of proportion, the value of x is,
⇒ x = 80
We have to given that;
In a triangle,
Perpendicular = 60
Now, By Pythagoras theorem we get;
60² = 36² + y²
3600 = 1296 + y²
y² = 3600 - 1296
y² = 2304
y = 48
Hence, By definition of proportion;
⇒ x / 48 = 60 / 36
⇒ x = 80
Thus, By definition of proportion, the value of x is,
⇒ x = 80
Learn more about the proportion visit:
https://brainly.com/question/1496357
#SPJ1
Smallest successive composites with gap
17, 73, 2, 19
Answers
Answer:
Well, the smallest successive composites with gap 17, 73, 2, and 19 would have to be:
1. $341 = 11 \times 31$
2. $458 = 2 \times 299$
3. $460 = 2^2 \times 5 \times 23$
4. $479 = 13 \times 37$
5. You buy a boat for $35,000 that * 10 points
depreciates in value at about 17%
per year. How much will it be worth
in 3 years?
Your answer
Answers
Answer:
9000
Step-by-step explanation:
how much money deposited now will provide payment of Rs. 15000 at the end of each half year for 10 years, if interest is 16% compounded six-monthly
Answers
The interest is 16% compounded semi-annually, is Rs. 121,179.10.
To determine how much money needs to be deposited now to provide a payment of Rs. 15,000 at the end of each half year for 10 years, we will use the formula for the present value of an annuity.
Present value of an annuity = (Payment amount x (1 - (1 + r)^-n))/rWhere:r = interest rate per compounding periodn = number of compounding periodsPayment amount = Rs. 15,000n = 10 x 2 = 20 (since there are 2 half years in a year and the payments are made for 10 years)
So, we have:r = 16%/2 = 8% (since the interest is compounded semi-annually)Payment amount = Rs. 15,000Using the above formula, we can calculate the present value of the annuity as follows:
Present value of annuity = (15000 x (1 - (1 + 0.08)^-20))/0.08 = Rs. 121,179.10Therefore, the amount that needs to be deposited now to provide payment of Rs. 15,000 at the end of each half year for 10 years, if the interest is 16% compounded semi-annually, is Rs. 121,179.10.
For more such questions on semi-annually
https://brainly.com/question/30573341
#SPJ8
Points A, B, C, and D are on circle O, as shown.
Answers
Given data:
The given figure of the circle.
The angle DCA is,
\(\begin{gathered} \angle DCA=\frac{1}{2}\angle AOD \\ =\frac{1}{2}(114^{\circ}) \\ =57^{\circ} \end{gathered}\)BD is diameter , it means the angle BCD is 90 degrees, the angle DBC is,
\(\begin{gathered} \angle DBC=90^{\circ}-40^{\circ} \\ =50^{\circ} \end{gathered}\)The angle BOC is,
\(\begin{gathered} \angle BOC=180^{\circ}-2\angle\text{OBC} \\ =180^{\circ}-2\angle DBC \\ =180^{\circ}-2(50^{\circ}) \\ =80^{\circ} \end{gathered}\)Thus, the third option is correct.
A crane is being created by four steel members (bold) and a cable, as shown in the diagram below. It is known that AC = 10 ft. AB = 8 ft, m/A=
40°, m/ CBD-65°, and m/ D=45°.
(a) Determine the length of support member BC to the nearest hundredth of a foot.
(b) Determine the length of the cable CD to the nearest hundredth of a foot.

Answers
Using law of cosine and Pythagorean theorem, the length of BC is 18 foot and CD is 12.3 foot
What is the length of BCa) To find the length of support member BC, we can use the Law of Cosines:
BC^2 = AC^2 + AB^2 - 2 * AC * AB * cos(m/C)
where m/C is the measure of angle C. We know that m/A = 40° and m/D = 45°, so m/C must be the supplementary angle to the sum of these angles:
m/C = 180° - (m/A + m/D) = 180° - (40° + 45°) = 95°
Substituting known values into the Law of Cosines equation, we have:
BC^2 = 10^2 + 8^2 - 2 * 10 * 8 * cos(95°)
BC^2 = 100 + 64 + 160
BC^2 = 324
BC = sqrt(324) = 18
So, the length of support member BC is 18 feet to the nearest hundredth of a foot.
b) To find the length of cable CD, we can use the Pythagorean Theorem:
CD^2 = BC^2 + AC^2 - 2 * BC * AC * cos(m/A)
Substituting known values into the equation, we have:
CD^2 = 18^2 + 10^2 - 2 * 18 * 10 * cos(40°)
CD^2 = 324 + 100 - 360 * cos(40°)
CD^2 = 424 - 360 * cos(40°)
Using the cosine formula, we can find the value of cos(40°):
cos(40°) = cos(90° - 40°) = sin(40°)
And using a reference table or calculator, we find that sin(40°) = 0.766
So, substituting the value of cos(40°) back into the equation for CD^2, we have:
CD^2 = 424 - 360 * 0.766
CD^2 = 424 - 276.56
CD^2 = 147.44
CD = sqrt(147.44) = 12.3
So, the length of cable CD is 12.3 feet to the nearest hundredth of a foot.
Learn more on cosine law here;
https://brainly.com/question/4372174
#SPJ1
Find the values of x for which the denominator is equal to zero for 2x^2+5/x^2-2x .
x = 0, x = 2
x = 1, x = 2
none
x = 2
Answers
Let's see
\(\\ \rm\rightarrowtail x^2-2x=0\)
\(\\ \rm\rightarrowtail x(x-2)=0\)
\(\\ \rm\rightarrowtail x=0\:or\:x-2=0\)
\(\\ \rm\rightarrowtail x=0\:or\:x=2\)
\( \green{••••••••••••••••••••••} \blue{••••••••••••••••••••••••••}\)
\( \sf {x^2 - 2x = 0} \)
\( \sf {x ( x - 2) = 0} \)
\( \sf {x = 0 \: or \: x-2 = 0} \)
\( \sf \green{ {x = 0 \: or \: x = 2}} \)
#CarryOnLearning
#LibreAngMatuto
Help fast please !! Represent the following sentence as an algebraic expression, where "a number" is the letter x. 4 is added to twice a number.
Answers
Case #3 Travel
A travel agency surveyed 140 families about
their favorite vacation spots.
Is it reasonable to say that 24 more
families chose Hawaii over Florida?
Explain.
Answers
Yes. It is reasonable to say that 24 more families chose Hawaii over Florida.
To say that 24 more families chose Hawaii over Florida implies that the number of families that chose Hawaii is greater than the families that chose Florida by 24.For example, if 30 families chose Florida, then the number of families that chose Hawaii will be 54 (30 + 24).Thus, it is very reasonable to conclude from the survey that 24 more families chose Hawaii over Florida.
Link to related question on making conclusions from mathematical calculations at https://brainly.com/question/22224175
Select the correct answer from each drop-down menu.
The area of the shaded square is
square inches. The length of the unshaded rectangle is
inches.
The estimated value of the length of the shaded square is
inches. The estimated value of the area of the unshaded rectangle is
square inches.
Answers
The completed statement with regards to the area of the square and the rectangle are;
The estimated value of the length of the shaded square is 5·√5 inches. The estimated value of the area of the unshaded rectangle is 175 square inches.
What is the area of a square?The area of a square is the product of the side lengths which are congruent, therefore;
Area of a square = Side length, s × Side length, s = s²
The possible figure in the question includes;
A shaded square that is 125 square inches
An adjacent unshaded rectangle, that share a side with the square that has a side length of 7·√5 inches
Please find attached the possible drawing of the figure in the question, (not drawn to scale) obtained from a similar question posted online, created with MS Word.
Therefore;
The side length of the square = √(125) inches = 5·√5 inches
The estimated value of the side length of the square is; 5·√5 inches
The area of a rectangle = Length × Width
The length of the rectangle = 7·√5 inches
The width of the rectangle = 5·√5 inches
Therefore;
The area of the unshaded rectangle, therefore is; 5·√5 × 7·√5 = 175
The estimated area of the unshaded rectangle is 175 square inches
Learn more on the area of a rectangle here: https://brainly.com/question/26303775
#SPJ1

find the number of ways that the digit 0,1,2and3 can be permuted to give rise to a number greater than 2000
Answers
12 or 128
by the way question is not complete
the answer is 128 , if repetition is allowed
and answer is 12 , if repetition is not allowed
3 Jack walk from Santa Clara to Polo Allo. Il took I hour 25 min to walk from Santa Clot to Los Altos. Than it took 25 minute of wal from los altos to Palo buto. He arrived in Palo alto at 2:45 P.M. of what time die Santa Clara ? he leave Santa clara
Answers
The time Jack left Santa Clara is 1 : 55 pm
What is word problem?A word problem in math is a math question written as one sentence or more. These statements are interpreted into mathematical equation or expression.
The time for Jack to walk to lose Altos is 25 min and he uses another 25mins to work to Palo alto.
Therefore, the total time he spent is
25mins + 25 mins = 50 mins
He arrived Palo at 2 :45 pm, therefore the time he left Santa Clare will be ;
2:45 pm = 14 :45
= 14:45 - 50mins
= 13:55
= 1 : 55pm
Therefore he left at 1:55 pm
learn more about word problem from
https://brainly.com/question/21405634
#SPJ1
What is the meaning of "\( \varphi (x,y)\) be \( y\wedge \phi (x)\) "?
![What is the meaning of "[tex] \varphi (x,y)[/tex] be [tex] y\wedge \phi (x)[/tex] "?](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/IEnaK9Mnw3ftGn7VoWymvKjzqCukNTp6.png)
Answers
The given passage provides a proof that the Separation Axioms follow from the Replacement Schema.
The proof involves introducing a set F and showing that {a: e X : O(x)} is equal to F (X) for every X. Therefore, the conclusion is that the Separation Axioms can be derived from the Replacement Schema.In the given passage, the author presents a proof that demonstrates a relationship between the Separation Axioms and the Replacement Schema.
The proof involves the introduction of a set F and establishes that the set {a: e X : O(x)} is equivalent to F (X) for any given set X. This implies that the conditions of the Separation Axioms can be satisfied by applying the Replacement Schema. Essentially, the author is showing that the Replacement Schema can be used to derive or prove the Separation Axioms. By providing this proof, the passage establishes a connection between these two concepts in set theory.
Learn more about axioms here:
https://brainly.com/question/2857184
#SPJ8
Gravel is being dumped from a conveyor belt at a rate of 35 ft3/min, and its coarseness is such that it forms a pile in the shape of a cone whose base diameter and height are always equal. How fast is the height of the pile increasing when the pile is 9 ft high? (Round your answer to two decimal places.)
Answers
Answer:
dh/dt ≈ 0.55 ft/min
Step-by-step explanation:
The volume is given by the formula ...
V = (1/3)πr²h
We have r = h/2, so the volume as a function of height is ...
V = (1/3)π(h/2)²h = (π/12)h³
Then the rates of change are related by ...
dV/dt = (π/4)h²·dh/dt
dh/dt = (4·dV/dt)/(πh²) = 4(35 ft³/min)/(π(9 ft)²)
dh/dt ≈ 0.55 ft/min