What are the solutions of the equation 3x + 8x=12
Answers
Answer: 0.917
Step-by-step explanation:
3x+8x=12
11x=12
1x=(11x/12)
1x=0.91666
1x=0.917
Related Questions
Which type of triangle will always have at least 1-fold reflectional symmetry?
right triangle
obtuse triangle
acute triangle
isosceles triangle
Answers
Answer:
Isosceles triangle I think
Step-by-step explanation:
The triangle that will always have at least 1-fold reflectional symmetry is the isosceles triangle. That is option D.
What is reflectional symmetry?Reflectional symmetry is found in geometric shapes that can be folded over onto itself along a line.
The isosceles triangle has only one line of symmetry or 1-fold reflectional symmetry.
Therefore, the triangle that will always have at least 1-fold reflectional symmetry is the isosceles triangle.
Learn more about symmetry here:
https://brainly.com/question/1002723
#SPJ9
i dont understand :/

Answers
Answer:
Step-by-step explanation:
same
Can the sum of the magnitudes of two vectors ever be equal to the magnitude of the sum of the same two vectors?.
Answers
No, the sum of the magnitudes of two vectors can never be equal to the magnitude of the sum of the same two vectors.
The magnitude of the sum of two vectors is determined by the vector addition process, which takes into account both the magnitudes and the directions of the vectors. The magnitude of the sum of two vectors is generally greater than or equal to the sum of their individual magnitudes.
Mathematically, for two vectors A and B, the magnitude of the sum (|A + B|) is given by the triangle inequality:
|A + B| ≤ |A| + |B|
Equality in the triangle inequality occurs only when the vectors are collinear, meaning they have the same direction or are in opposite directions. In such cases, the vectors can be scaled such that their magnitudes add up to the magnitude of their sum. However, in general, when vectors have different directions, the sum of their magnitudes will always be greater than the magnitude of their sum.
learn more about vectors here:
https://brainly.com/question/30958460
#SPJ11
Can somebody help me, please

Answers
Answer:
uh I don't even know what this is
Answer: x = 500
Step-by-step explanation:
Use the Pythagorean Theorem
a²+b²=c²
300² + 400² = x²
90000 + 160000 = x²
250000 = x²
√250000 = √x²
500 = x
hope i explained it :)
What is the likely means of measurement for the data in the chart below?
a. 100-meter run data
b. seconds
c. stop watch
d. 7 observations

Answers
Answer:
C
Step-by-step explanation:
I might be wrong. I hope it helps:)
Ms. Sanchez’s guests drank 5 3/4 gallons of pink lemonade in 1/4 hour. What was the average rate in gallons per hour which her guests drank the pink lemonade
Answers
Answer:
23 gallons per hour
Step-by-step explanation:
5 3/4 * 4 = 23
times the amount drank in 1/4 hours by 4 to get the amount drank in 1 hour
(1/4 * 4 = 1 hour (example))
The answer is 23
Suppose the distance an athlete throws a hammer follows a normal distribution with mean 50 feet and standard deviation 5 feet. What is the probability he throws it between 50 feet and 60 feet? Give your answer to 4 decimal places.?
Answers
If the distance an athlete throws a hammer follows a normal distribution with mean= 50 feet and standard deviation= 5 feet, then the probability he throws it between 50 feet and 60 feet is 0.4772
To find the probability he throws it between 50 feet and 60 feet, follow these steps:
We know that z = (x - μ) / σ, where μ = mean, σ = standard deviation and x = given value. Here, μ = 50 and σ = 5So, the z-score for 50 feet is:z = (x - μ) / σ ⇒z = (50 - 50) / 5 ⇒z = 0/5⇒ z = 0. The z-score for 60 feet is: z = (x - μ) / σ ⇒z = (60 - 50) / 5 ⇒z = 10 / 5 ⇒z = 2To find the probability that the athlete throws the hammer between 50 feet and 60 feet, we need to find the area under the normal distribution curve between these two z-scores using a standard normal distribution table. The area under the curve between z = 0 and z = 2 is 0.4772.Hence, the probability he throws a hammer between 50 feet and 60 feet is 0.4772
Learn more about normal distribution:
brainly.com/question/23418254
#SPJ11
please answer
4. Suppose that for 3MA Forecast, my Mean Absolute Deviation (MAD) is \( 3.0 \) and my Average Error (AE) is \( -2.0 \). Does my forecast fail the bias test? a. Yes b. No
Answers
The answer is: a. Yes, the forecast fails the bias test.
To determine whether the forecast fails the bias test, we need to compare the Average Error (AE) with zero.
If the AE is significantly different from zero, it indicates the presence of bias in the forecast. If the AE is close to zero, it suggests that the forecast is unbiased.
In this case, the Average Error (AE) is -2.0, which means that, on average, the forecast is 2.0 units lower than the actual values. Since the AE is not zero, we can conclude that there is a bias in the forecast.
Therefore, the answer is:
a. Yes, the forecast fails the bias test.
Learn more about bias test from
https://brainly.com/question/32000527
#SPJ11
An item is priced at $14.32. If the sales tax is 5%, what does the item cost including sales tax? If necessary, round to the nearest cent
Answers
$15.03
hope this helps !
freda is laying mulch in her garden. the garden is 8 feet by 12 feet and the mulch should be 3 inches deep. how much mulch does she need?
Answers
Answer:
288
Step-by-step explanation:
8x12x3
which choice is equvalent to the expression below 5^9.96
a. 5^9 • 5^96/10 • 5^9/100
b. 5^9•5^9/10•5^6/100•5^9/1000
c. 5^9+5^9/10+6^6/100
d. 5^9+9/10+9/10+6/1000
Answers
Answer:
B
Step-by-step explanation:
5^9•5^9/10•5^6/100•5^9/1000 = 5^(9+0.9+0.06+0.009) = 5^9.969
Another model for a growth function for a limited population is given by the Gompertz function, which is a solution of the differential equation dP/dt = c ln(K/P) P where c is a constant and K is the carrying capacity.
Answers
The rate of population growth is proportional to the logarithm of the ratio of the carrying capacity to the current population.
The Gompertz function is a solution of the differential equation:
dP/dt = c ln(K/P) P
where P(t) is the population at time t, c is a constant, and K is the carrying capacity, i.e., the maximum population that can be sustained by the available resources.
To solve this differential equation, we can use separation of variables:
dP/P ln(K/P) = c dt
Integrating both sides, we get:
∫ dP/P ln(K/P) = ∫ c dt
Integrating the left-hand side requires a substitution. Let u = ln(K/P), then du/dP = -1/P and the integral becomes:
-∫ du/u = -ln|u| = -ln|ln(K/P)|
The right-hand side is just:
c t + C
where C is an arbitrary constant of integration.
Putting these together, we get:
-ln|ln(K/P)| = ct + C
Taking the exponential of both sides, we get:
|ln(K/P)| = e^(-ct-C)
Using the absolute value is unnecessary, since ln(K/P) is always positive, so we can drop the absolute value and write:
ln(K/P) = e^(-ct-C)
Solving for P, we get:
P = K e^(-e^(-ct-C))
This is the Gompertz function, which gives the population as a function of time, under the assumption that the rate of population growth is proportional to the logarithm of the ratio of the carrying capacity to the current population.
To learn more about unnecessary visit:
https://brainly.com/question/29972055
#SPJ11
Can any kind soul help me ASAP!

Answers
Answer:
the answer is B
x = 1
Step-by-step explanation:
the symmetry is in the middle of the curve like a mirror and the equation of the mirror or symmetry line is x=1
A baker initially makes 10 loaves of bread and sells 2 loaves each day.
How many loaves of bread does the baker have at the end of the second day?
Answers
Answer:6
Step-by-step explanation:
day one-2 bread
day two-4 bread
10-4=6
6 at the end of the day
The number of loaves of bread remaining at the end of second day = 6 loaves of bread
What is an Equation?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the equation be represented as A
Now , the value of A is
Let number of loaves of bread remaining at the end of second day be A
The total number of loaves of bread = 10 loaves
The number of loaves of bread sold each day = 2 loaves
Substituting the values in the equation , we get
So , the number of loaves of bread remaining at end of first day = 10 - 2 = 8
Now , the number of loaves of bread remaining at end of second day = 8 -2
The number of loaves of bread remaining at the end of second day = 6
Therefore , the value of A is 6 loaves of bread
Hence , the equation is A = 6 loaves
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ5
336,765=3,14×0.55×(l+0.55) please help
Answers
Answer:
l = 194999.45
Step-by-step explanation:
I'm going to assume that you meant 3.14 by 3,14.
336,765 = 3.14 × 0.55 × (l + 0.55)
336,765 ÷ (3.14 × 0.55) = l + 0.55
(336,765 ÷ (3.14 × 0.55)) - 0.55 = l
l = 194999.45
The diagram shows part of a fan. OFG and OAD are sectors, centre 0, with radius 18 cm and sector angle 40° B, C, H and E lie on a circle, centre O and radius 6 cm. Calculate the shaded area.
Answers
The area of a shape is the amount of space on it:
The shaded area is 314 square centimeters
How to determine the shaded areaStart by calculating the area of sectors OFG and OAD using:
\(A = \frac{\theta}{360} * \pi r^2\)
So, we have:
\(OFG = \frac{40}{360} * \pi * 18^2\)
\(OFG = 36\pi\)
Also, we have:
\(OAD = \frac{40}{360} * \pi * 18^2\)
\(OAD = 36\pi\)
Next, calculate the area of the sectors BOE and COH
Note that the radius of these sectors is 6 cm.
So, we have:
\(COH =BOE = \frac{140}{360} * \pi * 6^2\)
\(COH = BOE = 14\pi\)
The shaded area is then calculated as:
\(Shaded = OFG + OAD + COH + BOE\)
This gives
\(Shaded =36\pi + 36\pi + 14\pi + 14\pi\)
\(Shaded =100\pi\)
The equation becomes
\(Shaded =100 * 3.14\)
\(Shaded = 314\)
Hence, the shaded area is 314 square centimeters
Read more about areas at:
https://brainly.com/question/14989383
What is 3/6 + 2/6
• 5/12
•3/8
•5/6
Answers
What do 32x4x3x2÷5 equal 20 points and brainliest if right.
Answers
Answer:
153.6
Step-by-step explanation:
Answer:
153.6
Step-by-step explanation:
32x4=128
128x3=384
384x2=768
768/5=153.6
The pearson correlation is calculated for a sample of n = 25 individuals. what value of df should be used to determine whether or not the correlation is significant?
Answers
The correlation is a significant non-zero value.
The number of samples is n.
n = 25
The correlation of the coefficient is r.
r = -0.40
When correlation is significant,
\(H _{0} : p = 0\)
When correlation is non-zero,
\(H _{ \alpha } : p ≠0\)
The test statistic is,
\(TS = \frac{r \times \sqrt{n - 2} }{ \sqrt{1 - r {}^{2} } } \)
\( = \frac{0.4 \times \sqrt{25 - 2} }{ \sqrt{1 - ( - 0.4) ^{2} } } \)
\( = \frac{ - 1.918 }{ \sqrt{0.84} } \)
= -2.093
The test statistic is -2.093.
The correlation is,
\(H _{ \alpha } : - 2.93 ≠0\)
The correlation is not equal to zero and is significant.
Therefore, the correlation is a significant non-zero value.
To know more about correlation, refer to the below link:
https://brainly.com/question/13956667
#SPJ4
Use the Lagrange coefficient method to find the sub-values of x and y respectively? (10%) max f(x.y.z)=x²z+yz s.t 2x+y+z=5
Answers
Using the Lagrange coefficient method, the sub-values are x = 1 and y = 3 - λ, where λ can have any value.
To find the sub-values of x and y using the Lagrange coefficient method, we need to set up the Lagrange function by incorporating the given objective function and constraint equation. Let's proceed step by step.
Define the objective function and constraint equation:
Objective function: f(x, y, z) = x²z + yz
Constraint equation: g(x, y, z) = 2x + y + z - 5 = 0
Set up the Lagrange function:
L(x, y, z, λ) = f(x, y, z) - λ * g(x, y, z)
L(x, y, z, λ) = x²z + yz - λ(2x + y + z - 5)
Find the partial derivatives
∂L/∂x = 2xz - 2λ = 0 -- (1)
∂L/∂y = z - λ = 0 -- (2)
∂L/∂z = x² + y - λ = 0 -- (3)
∂L/∂λ = -(2x + y + z - 5) = 0 -- (4)
Solve the system of equations
From equation (2), we get z = λ.
Substituting z = λ in equation (3), we have x² + y - λ = 0.
Rearranging equation (1), we get x = λ/z = λ/λ = 1.
Substituting x = 1 in equation (4), we have 2(1) + y + λ = 5.
Simplifying, we get y + λ = 3.
Now, we have the following equations
x = 1 -- (5)
y + λ = 3 -- (6)
z = λ -- (7)
2(1) + y + λ = 5 -- (8)
From equation (6), we can solve for λ:
y = 3 - λ -- (9)
Substituting equation (9) into equation (8):
2(1) + (3 - λ) + λ = 5
2 + 3 - λ + λ = 5
5 = 5
The equation 5 = 5 is always true. It indicates that λ can have any value.
Determine the sub-values of x and y:
From equation (5), we have x = 1.
Substituting y = 3 - λ (from equation (9)), we have y = 3 - λ.
Substituting z = λ (from equation (7)), we have z = λ.
Therefore, the sub-values of x and y are x = 1 and y = 3 - λ, respectively.
To know more about Lagrange coefficient method:
https://brainly.com/question/32251301
#SPJ4
Goodnight thanks Brainly!!
Answers
Answer:
Good Night comrade !!
Step-by-step explanation:
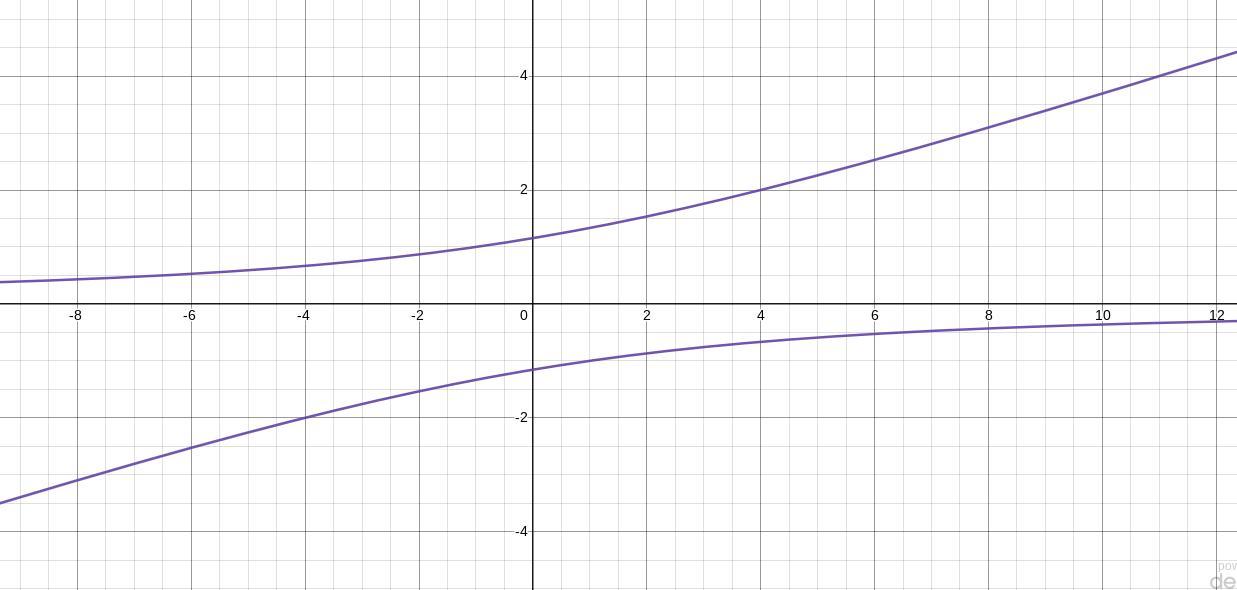
sketch the graph of xy = 3y² - 4
Answers
Answer:
xy = 3y² - 4
Step-by-step explanation:
Hope it is helpful....
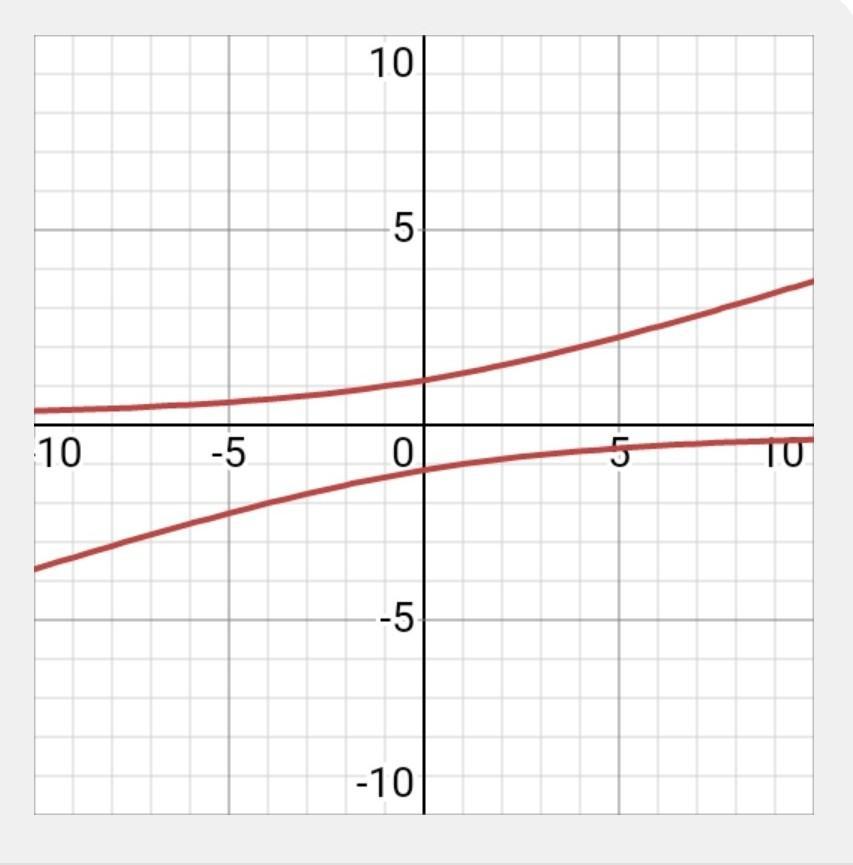
In the file i have attached, you will find the equation graphed, hope this helps.
C.
The high temperature this Sunday is expected to be 5 degrees warmer than the
high temperature this Saturday. Using the line c = 2t - 89, how many more
cups of lemonade should Lin expect to sell on Sunday than Saturday? Explain or
show your reasoning.
Answers
Answer: 10 more
Step-by-step explanation:
Because 2 x 79 -89 =69
69-59=10
Use the method of variation of parameters to determine the general solution of the given differential equation. y" - 2y" -y + 2y = est NOTE: Use C₁, C2, and cg as arbitrary constants. y(t) = C₁ e + c₂ et + c3 € e²t + est (9 e¹ - 5) 45 t X
Answers
The general solution for the given differential equation is: \(y(t) = y_h(t) + y_p(t)\)
\(= (C_1 + C_2t)e^t + C_3e^t + (C_4t - (1/2)e^st)te^t\)
To find the general solution of the given differential equation using the method of variation of parameters, we assume a solution of the form y(t) = C₁\(e^(rt),\) where C₁ is an arbitrary constant and r is a constant to be determined.
The characteristic equation for the homogeneous equation is obtained by substituting y(t) = \(e^(rt)\)into the homogeneous equation:
\(r^2 - 2r - 1 + 2 = 0\)
Simplifying the equation, we have:
\(r^2 - 2r + 1 = 0\)
\((r - 1)^2 = 0\)
This equation has a repeated root r = 1.
Therefore, the homogeneous solution is given by y_h(t) = (C₁ + C₂t)e^t, where C₁ and C₂ are arbitrary constants.
Next, we find the particular solution using the method of variation of parameters. We assume the particular solution has the form y_p(t) = \(u_1(t)e^t + u_2(t)te^t.\)
To find u₁(t) and u₂(t), we substitute y(t) and its derivatives into the differential equation:
y" - 2y' - y + 2y =\(e^st\)
Taking the derivatives of \(y_p(t)\), we have:
\(y_p'(t) = u_1'(t)e^t + u_1(t)e^t + u_2'(t)te^t + u_2(t)te^t + u_2(t)e^t\)
\(y_p"(t) = u_1"(t)e^t + 2u_1'(t)e^t + u_1(t)e^t + u_2"(t)te^t + 2u_2'(t)e^t + 2u_2(t)e^t + u_2(t)e^t\)
Substituting these derivatives into the differential equation, we get:
u₁"(t)e^t + 2u₁'(t)e^t + u₁(t)e^t + u₂"(t)te^t + 2u₂'(t)e^t + 2u₂(t)e^t + u₂(t)e^t - 2(u₁'(t)e^t + u₁(t)e^t + u₂'(t)te^t + u₂(t)te^t + u₂(t)e^t) - (u₁(t)e^t + u₂(t)te^t) + 2(u₁(t)e^t + u₂(t)te^t) = e^st
Simplifying and grouping the terms, we have:
u₁"(t)\(e^t\)+ 2u₂'(t)\(e^t\) = 0
\(u_1"(t)e^t + 2u_2"(t)e^t - 2u_1'(t)e^t - 2u_2'(t)te^t = e^st\)
To solve this system of equations, we can equate the coefficients of like terms on both sides. We have:
For e^t:
u₁"(t) - 2u₁'(t) = 0 ...(1)
For te^t:
2u₂"(t) - 2u₂'(t) = e^st ...(2)
Solving equation (1), we find the general solution:
u₁(t) = C₃e^t, where C₃ is an arbitrary constant.
Solving equation (2), we use the method of undetermined coefficients to find a particular solution for u₂(t). Assume u₂(t) = C₄t + C₅. Substituting this into equation (2), we get:
2(C₄) - 2(C₄ + C₅) = \(e^st\)
Simplifying, we have:
-2C₅ = \(e^st\)
Therefore, C₅ = -1/2e^st.
The particular solution for u₂(t) is u₂(t) = C₄t - \((1/2)e^st,\) where C₄ is an arbitrary constant.
Finally, the general solution for the given differential equation is:
\(y(t) = y_h(t) + y_p(t)\)
= (C₁ + C₂t)\(e^t\)+ C₃\(e^t\) + (C₄t - \((1/2)e^st)te^t\)
This is the general solution of the given differential equation using the method of variation of parameters. The arbitrary constants are C₁, C₂, C₃, and C₄.
Learn more about Differential equations here:
https://brainly.com/question/1164377
#SPJ11
Question 1
If your train travels at 65 miles per
hour for 3.5 hours, how far will it
go?
Answers
If your train travels at 65 miles per hour for 3.5 hours, it go 227.5 miles.
What is Speed ?
Velocity is the pace and direction of an object's movement, whereas speed is the time rate at which an object is travelling along a path. In other words, velocity is a vector, whereas speed is a scalar value.
Given:
Speed S = 65 miles per hour
Time T = 3.5 hours
We know that,
S= D/T Where D is the distance traveled.
Therefore,
65 miles per hour = D/ 3.5 hours
D = 65 x 3.5 miles
=227.5 miles
To learn more about velocity click on the link below:
https://brainly.com/question/21729272
#SPJ1
The length of a cell phone is 1. 21. 2 inches and the width is 3. 43. 4 inches. The company making the cell phone wants to make a new version whose length will be 1. 681. 68 inches. Assuming the side lengths in the new phone are proportional to the old phone, what will be the width of the new phone?.
Answers
Assuming the side lengths in the new phone are proportional to the old phone Then the width of the new phone will be 4.760 inches
Define Proportions
A direct proportion is a relation between variables where their ratio is a constant value.
The original length of a cell phone was L=1.2 inches and the original width was 3.4inches.
A new version of the cell phone is to be released with proportional dimensions with respect to the original cell phone.
We are given the length of the new phone L'=1.68 inches. The ratio of the lengths is 1,2/1.68=0.71428
The new width should be W'=3.4/0.71428=4.760 inches
The width of the new phone will be 4.760 inches
learn more about length here
https://brainly.com/question/20063943
#SPJ4
a group of wine enthusiasts taste-tested a pinot noir wine from oregon. the evaluation was to grade the wine on a 0-to-100-point scale. a wine rated above 90 is considered truly exceptional. the results follow: a. compute the sample mean, the sample standard deviation, and the sample median. you may use excel for the calculations; if you do so, please upload your excel sheet with your homework solutions. b. construct a histogram and a boxplot for these data and comment on any important features that you notice. you can create by hand, or using excel or minitab. include histograms and boxplots in the pdf document submission c. what proportion of the taste-tasters considered this particular pinot noir truly exceptional?
Answers
The sample mean is 89.45, the sample standard deviation is 2.327, and the sample median is 91 and the leaf plot of the data is illustrated below.
The sample standard deviation is a measure of how much the ratings vary from the sample mean. It tells us how spread out the data is. A larger standard deviation means the data is more spread out, while a smaller standard deviation means the data is more tightly clustered around the mean.
To calculate the sample standard deviation, we first need to calculate the variance. The variance is the average of the squared differences between each rating and the mean. The formula for variance is:
variance = (sum of (rating - mean)²) / (number of ratings - 1)
In this case, the sum of the squared differences is 301.9, and there are 39 degrees of freedom (40 ratings minus 1), so the variance is 7.741. To get the sample standard deviation, we take the square root of the variance. In this case, the sample standard deviation is approximately 2.78.
The sample median is the middle rating when the ratings are arranged in order from lowest to highest. In this case, there are 40 ratings, so the median is the average of the 20th and 21st ratings, which are both 91.
Finally, we can determine what proportion of the taste-tasters considered this particular pinot noir truly exceptional (above 90 points). To do this, we count the number of ratings that are above 90 and divide by the total number of ratings. In this case, there are 30 ratings above 90, so the proportion is 30/40, or 0.75. This means that 75% of the taste-tasters considered this pinot noir truly exceptional.
To know more about standard deviation here
https://brainly.com/question/16555520
#SPJ4
Complete Question:
A group of wine enthusiasts taste-tested a pinot noir wine from Oregon. The evaluation was to grade the wine on a 0-to-100-point scale. The results follow. Construct a stemand- leaf diagram for these data and comment on any important features that you notice. Compute the sample mean, the sample standard deviation, and the sample median. A wine rated above 90 is considered truly exceptional. What proportion of the taste-tasters considered this particular pinot noir truly exceptional?
94 90 92 91 91 86 89 91 91 90
90 93 87 90 91 92 89 86 89 90
88 95 91 88 89 92 87 89 95 92
85 91 85 89 88 84 85 90 90 83


There are 630 calories in seven ounces of a certain ice cream. How many calories are
there in two pounds?
1 pound = 16 ounces
Before
you try that problem, answer the question below.
How many ounces will you need to find the number of
calories for?
What’s the answer?
Answers
Answer:
Hello mate here’s the answer 32 ounces
Step-by-step explanation:
2 pounds = 2x1(1 pound)
=2x(16 ounces)
=32 ounces
where does the line cross in the equation y=2x=12
Answers
Work out the equation of the line which has a gradient of 1/2 and passes through the point (2, -5)
Answers
Answer:
y=½x-6
Step-by-step explanation:
m= ½
equation of the line: y-y1=m(x-x1)
y+5=½(x-2)
y=½x-6
Answer:
\(y =\dfrac{1}{2}x-6\)
Step-by-step explanation:
Point-slope formula
\(y-y_1=m(x-x_1)\)
where:
\(m\) = slope (gradient)\((x_1,y_1)\) = point on the lineGiven:
Gradient (m) = ¹/₂Point = (2, -5)Substitute the given values into the formula:
\(\begin{aligned}y-y_1 & =m(x-x_1)\\\\\implies y-(-5) & =\dfrac{1}{2}(x-2)\\\\y+5 & =\dfrac{1}{2}x-1\\\\y & =\dfrac{1}{2}x-1-5\\\\y & =\dfrac{1}{2}x-6\end{aligned}\)