Answers
Answer:
As shown in picture, the graph starts from 0 and goes to + infinity.
=> Domain: [0, + infinity)
=> Range: [0, + infinity)
Hope this helps!
:)
Related Questions
What is the approximate length of minor arc JH? Round to the nearest tenth of a centimeter. 3. 5 cm 6. 9 cm 21. 6 cm 46. 8 cm.
Answers
WILL MARK BRAINLIEST!!!!20 POINTS!!!!URGENT!!!

Answers
Answer:
the firsts third and last one
Step-by-step explanation:
hope this helped
A sofa is 7 feet 5 inches long. How many inches is the sofa?
Answers
89 inches!
Because each foot is 12 inches and 12*7=84 and 84+5=89!
+18 pts
An observer (O) spots a plane (P) taking off from a local airport and flying at a 33° angle horizontal to her line of sight and located directly above a tower (T). The observer also notices a bird (B) circling directly above her. If the distance from the plane(P) to the tower (T) is 7,000 feet, how far is the bird (B) from the plane (P)? Round to the nearest whole number.
Help please !
Answers
Find attached to this answer, the appropriate diagram that would help us better understand the question
Answer:
10779 feet
Step-by-step explanation:
We would be using the Trigonometric function called Tangent to solve this question.
tan θ = Opposite side / Adjacent side
From the attached diagram,
θ = 33°
Opposite side = 7000 feet
Adjacent side = the distance of bird (B) from the plane (P) = unknown
tan 33° = 7000 feet / Adjacent side
Cross multiply
tan 33° × Adjacent side = 7000 feet
divide both sides by tan 33°
Adjacent side = 7000 feet / tan 33°
Adjacent side = 10779.054747 feet.
Approximately = 10779 feet.
Therefore, the distance of bird (B) from the plane (P) to the nearest whole number is 10779 feet.

Find the angle measure and round to the nearest Tenth.
cos0 = 7/10
x = ? degrees
Answers
Given f (x) = x2 + 5x + 6, what is [picture included] equal to?
h2 + 14h
2x + h + 5
h + 4
9 + h
![Given f (x) = x2 + 5x + 6, what is [picture included] equal to? h2 + 14h 2x + h + 5 h + 4 9 + h](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/SGIFk4uiNO6yoLEmhBpOoJsAMqETru3R.png)
Answers
The difference quotient evaluated in x = 2 gives:
[ f(2 + h) - f(2)]/h = h + 9
So the last option is the correct one.
How to find the difference quotient evaluated in 2?
Here we know the function:
f(x) = x^2 + 5x + 6
And we want to find the difference quotient:
[ f(2 + h) - f(2)]/h
Let's evaluate the function:
f(2 + h) = (2 + h)^2 + 5*(2 + h) + 6
= 2^2 + h^2 + 4h + 10 + 5h + 6
= h^2 + 9h + 20
f(2) = 2^2 + 5*2 + 6
f(2) = 4 + 10 + 6 = 20
Then we have:
[ f(2 + h) - f(2)]/h
[h^2 + 9h + 20 - 20]/h
[h^2 + 9h ]/h
Taking the quotient we get:
[h^2 + 9h ]/h = h + 9
So the correct option is the last one.
Learn more about the difference quotient:
https://brainly.com/question/24922801
#SPJ1
There are 79 students at arlington high school who play a winter sport of those athletes 11 are on the hockey team. what is the probability that a randomly selected winter athlete is on the ice hockey team?
Answers
In this case, the probability that a randomly selected winter athlete is on the ice hockey team is equal to `11/79`, which can be expressed as a fraction or a decimal.
There are 79 students in Arlington High School playing winter sports. Of those athletes, 11 are on the ice hockey team. Therefore, the probability that a randomly selected winter athlete is on the ice hockey team is equal to:
`P(H) = 11/79`
In probability theory, probability is the measure of the likelihood of an event happening.
It is denoted as P(A), where A is the event whose probability is calculated.
The probability of an event occurring is a number between 0 and 1.
The probability of event A is expressed as P(A), where 0 ≤ P(A) ≤ 1.
To learn more on probability :
https://brainly.com/question/13604758
#SPJ11
the volume of the small cube below is 1cm^3 estimate the volume of the cuboid

Answers
The volume of the cuboid to be approximately 1.8cm³.
In this case, we are given that the volume of the small cube is 1cm³. Therefore, using the formula, we can solve for the length of its side as follows:
1cm³ = s³
Taking the cube root of both sides: ∛(1cm³) = ∛(s³) 1cm = s
Hence, the length of the side of the small cube is 1cm.
Then, we can estimate the other two dimensions of the cuboid as follows:
• The width (w) could be a little more than the length of the side of the small cube, say 1.2a.
• The height (h) could also be a little more than the length of the side of the small cube, say 1.5a.
Therefore, using the formula for the volume of a cuboid, we can estimate the volume of the cuboid as follows:
V = lwh V = a × 1.2a × 1.5a V = 1.8a³
Substituting the value of 'a' as 1cm, we get:
V ≈ 1.8cm³
To know more about volume here
https://brainly.com/question/11168779
#SPJ1
A population of 60 foxes in a wildlife preserve quadruples in size every 12 years. The function y = 60.4*, where x is the number of 12-year periods, models the population growth. How many foxes will there be after 24 years? After 24 years there will be foxes. (Type a whole number.)
Answers
Answer:
960 foxes after 24 years
Step-by-step explanation:
given
y = 60 × \(4^{x}\) models the situation
there are 2 12- year periods in 24 years , then x = 2 , so
y = 60 × 4² = 60 × 16 = 960
there will be 960 foxes after 24 years
I need help what is the answer?

Answers
Answer:
#3
Step-by-step explanation:
QUICK PLSSS im bout to be grounded

Answers
Answer:
35
Step-by-step explanation:
what temperature is halfway between -23°F and +23°F
Answers
Answer:
The is 0 ur welcome
Step-by-step explanation:
ur welcome pls 5 star it
two concentric circles have radii 11 and 22 two points on the outer circle are chosen independently and uniformly at random. what is the probability that the chord joining the two points intersects the inner circle?
Answers
Answer: Two concentric circles have radii $1$ and $2$. Two points on the outer circle are chosen independently and uniformly at random. What is the probability that the chord joining the two points intersects the inner circle?
$\textbf{(A)}\ \frac{1}{6}\qquad \textbf{(B)}\ \frac{1}{4}\qquad \textbf{(C)}\ \frac{2-\sqrt{2}}{2}\qquad \textbf{(D)}\ \frac{1}{3}\qquad \textbf{(E)}\ \frac{1}{2}\qquad$
Solution
Let the center of the two circles be $O$. Now pick an arbitrary point $A$ on the boundary of the circle with radius $2$. We want to find the range of possible places for the second point, $A'$, such that $AA'$ passes through the circle of radius $1$. To do this, first draw the tangents from $A$ to the circle of radius $1$. Let the intersection points of the tangents (when extended) with circle of radius $2$ be $B$ and $C$. Let $H$ be the foot of the altitude from $O$ to $\overline{BC}$. Then we have the following diagram.
[asy] scale(200); pair A,O,B,C,H; A = (0,1); O = (0,0); B = (-.866,-.5); C = (.866,-.5); H = (0, -.5); draw(A--C--cycle); draw(A--O--cycle); draw(O--C--cycle); draw(O--H,dashed+linewidth(.7)); draw(A--B--cycle); draw(B--C--cycle); draw(O--B--cycle); dot("$A$",A,N); dot("$O$",O,NW); dot("$B$",B,W); dot("$C$",C,E); dot("$H$",H,S); label("$2$",O--(-.7,-.385),N); label("$1$",O--H,E); draw(circle(O,.5)); draw(circle(O,1)); [/asy]
We want to find $\angle BOC$, as the range of desired points $A'$ is the set of points on minor arc $\overarc{BC}$. This is because $B$ and $C$ are part of the tangents, which "set the boundaries" for $A'$. Since $OH = 1$ and $OB = 2$ as shown in the diagram, $\triangle OHB$ is a $30-60-90$ triangle with $\angle BOH = 60^\circ$. Thus, $\angle BOC = 120^\circ$, and the probability $A'$ lies on the minor arc $\overarc{BC}$ is thus $\dfrac{120}{360} = \boxed{\textbf{(D)}\: \dfrac13}$.
See Also
May I get help please

Answers
y =4
your answer will be 4
Answer:
y = 4Step-by-step explanation:
The line that is parallel to the line y = 9, and passes through (-2, 4)
Given line is horizontal line, and the parallel line is also horizontal
Since it passes through point with y-coordinate of 4, this is the line:
y = 4Please help me with this question please help

Answers
Let Ln denote the left-endpoint sum using n subintervals. Compute the indicated left sum for the given function on the indicated interval. (Round your answer to four decimal places.) L4 for f(x) =-11 on [4, 5]
Answers
the left-endpoint sum using four subintervals for the function f(x) = -11 on the interval [4, 5] is -2.75.
To compute the left-endpoint sum using n subintervals, we partition the interval [4, 5] into n equal subintervals of length Δx = (5-4)/n = 1/n. Then, we evaluate the function at the left endpoint of each subinterval and multiply by the width of the subinterval, and finally sum up these values.
For the function f(x) = -11 on [4, 5], we have:
Δx = 1/n
x0 = 4
xi = x0 + iΔx = 4 + i/n, for i = 1, 2, ..., n.
The left endpoint of each subinterval is xi-1, so we have:
L_n = Δx [ f(x0) + f(x1) + ... + f(x_{n-1}) ]
= Δx [ f(4) + f(4 + 1/n) + f(4 + 2/n) + ... + f(4 + (n-1)/n) ]
= (1/n) [ -11 + (-11) + ... + (-11) ] (there are n terms)
= -11/n
To find L4, we plug in n=4 into the formula we just derived:
L4 = -11/4 = -2.75 (rounded to four decimal places)
To know more about left-endpoint sum, refer here:
https://brainly.com/question/22709871
#SPJ11
Bacteria growth. A colony of bacteria is grown under ideal conditions in a laboratory so that the population increases exponentially with time. At the end of 3 h there are 10,000 bacteria. At the end of 5 h there are 40,000 bacteria. How many bacteria were present initially
Answers
Answer:
1250 bacteria
Step-by-step explanation:
The formula for Exponential Growth is given as:
P(t)= Poe^rt
Where
P(t) = Population after time t
Po = Initial Population
r = growth rate
t = time
Hence, solving for the above question , we have to find Po
Making Po the subject of the formula
Po = P(t)/e^rt
Step 1
Find the Exponential growth rate
At the end of 3 h there are 10,000 bacteria.
Hence:
Po = 10000/e^3r.... Equation 1
At the end of 5 h there are 40,000 bacteria.
Po = 40000/e^5r..... Equation 2
Equating both equations together,
10000/e^3r = 40000/e^5r
Hence:
e^5r/e^3r = 40000/10000
e^2r = 4
Take the In of both sides
In (e^2r) =In 4
2r= In 4
r = In 4/2
r = In 2
Step 2
Solve for Po(Initial Population)
Using Equation 2
Po = 40000/e^5r..... Equation 2
r = In2
Po = 40000/e^5 × In 2
Po = 40000/2⁵
Po = 1250 bacteria.
Therefore, they was 1250 bacteria initially
What is pooled mean standard error?
Answers
The pooled mean standard error is a measure of the variability associated with the difference between two group means in a statistical hypothesis test with equal variances.
The pooled mean standard error is a measure of the variability or uncertainty associated with the difference between two group means in a statistical hypothesis test, where the two groups have equal variances. Specifically, it is the standard error of the difference between the means of two independent samples, calculated by combining the standard errors of the two sample means into a single estimate.
The formula for the pooled mean standard error is:
SEp = \(\sqrt{ [ (s1^2/n1) + (s2^2/n2) ]}\)
where SEp is the pooled mean standard error, s1 and s2 are the standard deviations of the two samples, n1 and n2 are the sample sizes, and sqrt represents the square root function.
The pooled mean standard error is used in the calculation of the t-statistic in a two-sample t-test, which is used to test the hypothesis that there is a significant difference between the means of the two groups. By accounting for the variability of both groups, the pooled mean standard error provides a more accurate estimate of the standard error of the difference between the means, which in turn allows for more precise hypothesis testing.
Learn more about standard error here:
https://brainly.com/question/30667112
#SPJ4
the weights of maine lobsters at the time of their catch are normally distributed with a mean of 1.8 lb and a standard deviation of 0.25 lb. what is the probability that a randomly selected lobster weighs
Answers
The probability that a randomly selected lobster weighs more than 2.5 lb is 0.0026.
Let X be the weight of a randomly selected Maine lobster. We know that X is normally distributed with mean μ = 1.8 lb and standard deviation σ = 0.25 lb.
We need to find the probability that a randomly selected lobster weighs
a) less than 1.5 lb
b) between 1.6 and 2 lb
c) more than 2.5 lb
To solve these problems, we need to standardize the variable X using the standard normal distribution
Z = (X - μ) / σ
a) To find the probability that a randomly selected lobster weighs less than 1.5 lb, we need to find P(X < 1.5). Standardizing X, we have
Z = (1.5 - 1.8) / 0.25 = -1.2
Using a standard normal distribution table or calculator, we find that P(Z < -1.2) = 0.1151.
Therefore, the probability that a randomly selected lobster weighs less than 1.5 lb is 0.1151.
b) To find the probability that a randomly selected lobster weighs between 1.6 and 2 lb, we need to find P(1.6 < X < 2). Standardizing X, we have
Z1 = (1.6 - 1.8) / 0.25 = -0.8
Z2 = (2 - 1.8) / 0.25 = 0.8
Using a standard normal distribution table or calculator, we find that P(-0.8 < Z < 0.8) = 0.5328
Therefore, the probability that a randomly selected lobster weighs between 1.6 and 2 lb is 0.5328.
c) To find the probability that a randomly selected lobster weighs more than 2.5 lb, we need to find P(X > 2.5). Standardizing X, we have:
Z = (2.5 - 1.8) / 0.25 = 2.8
Using a standard normal distribution table or calculator, we find that P(Z > 2.8) = 0.0026.
Learn more about probability here
brainly.com/question/11234923
#SPJ4
the diagram shows a prism work out the volume???
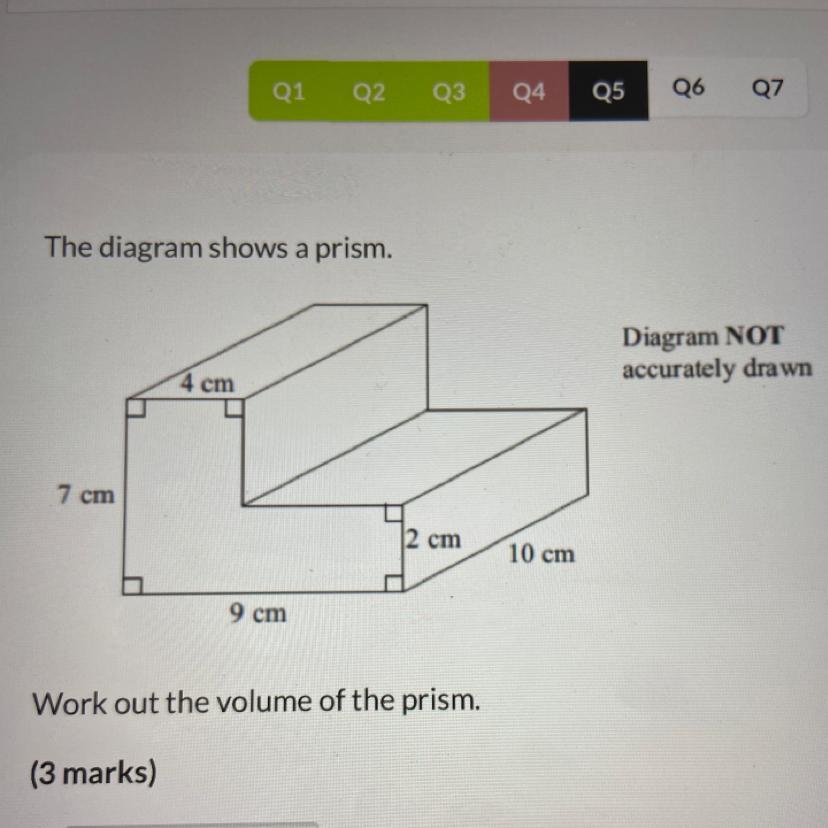
Answers
Answer:
Volume is equal to
L×W×H
=(10×9×7)cm
=90×7
=630
The volume of the prism is 980cm3.
We are given that;
The dimensions= 4*7*9*2*10cm
Now,
A rectangular prism is a three-dimensional shape that has two at the top and bottom and four are lateral faces.
The volume of a rectangular prism=Length X Width X Height
Volume of upper prism;
=5*4*40
=800cm3
Volume of lower prism;
=2*9*10
=180cm3
Total volume= upper volume + lower volume
=980cm3
Therefore, by the rectangular prism the answer will be 980cm3.
Learn more about a rectangular prism;
https://brainly.com/question/21308574
#SPJ2
What is distance between (-4,6) and (3, -7)?
Answers
Answer:
Let(-4,6)and (3,-7) be named as A and B
A(-4,6) (x1,y1)
B(3,-7) (x2,y2)
distance between AB= square root(x2-x1)^2+(y2-y1)^2
AB= square root(3-(-4)^2+(-7)-6)^2
AB= square root(3+4)^2+(-13)^2
AB= square root(7)^2+169
AB= square root(49+169)
AB= square root218
AB=14.76 Answer!!!
A unit rate is a rate in which the unit in the denomonater is
A:1
B:2
C:0
D:3
Answers
Answer:
the answer is A hope this helped
Step-by-step explanation:
The following equations are given
Equation #1 3x+z+y=8
Equation #2 5y-x=-7
Equation #3 3z+2x-2y=15
Equation #4 4x+5y-2z=-3
a. is it possible to solve for any of the variables using only Equation #1 and Equation #27 Explain your answer. If possible, solve for the variables using only equations #1 and #2
b. is it possible to solve for any of the variables using only Equation #1, Equation #2, and Equation #37 Explain your answer if possible, solve for the variables using only equations #1, #2, and #3
c. if you found solutions in part b, do these solutions also hold for Equation #4?
Answers
The required values are x = 2, y = -1 and z = 3
What are system of equations?In mathematics, a set of simultaneous equations, also known as a system of equations or an equation system, is a finite set of equation for which common solutions are sought.
The given set of equations are :
Equation #1 3x+z+y=8
Equation #2 5y-x=-7
Equation #3 3z+2x-2y=15
Equation #4 4x+5y-2z=-3
a. It is not possible to solve for any of the variables using only Equation #1 and Equation #2
As there are 3 variables x,y and z in the given system of equations so we need 3 equations.
If we take only Equation #1 and Equation #2 , Equation #1 contains 3 variables and Equation #2 contains only 2 variable.
b. it is possible to solve for any of the variables using only Equation #1, Equation #2, and Equation #3
As there are 3 variables x,y and z in the given system of equations so we need 3 equations.
So, taking Equation #1, Equation #2, and Equation #3
Equation #1 3x+z+y=8
Equation #2 5y-x=-7
Equation #3 3z+2x-2y=15
From, Equation #1 we have
z =8 - 3x - y
Put this in Equation #3 we get,
7x +5y = 9
Solving Equation #1, Equation #2 we get,
x = 2, and
y = -1
Again put the values of x and y in Equation #1 we get,
z = 3
Hence , the required values are x = 2, y = -1 and z = 3
More about system of equations :
https://brainly.com/question/2273153
#SPJ1
Scott Mason purchased a 4 unit apartment building as an investment before he retired. From the rent he collects each month, Scott pays out $500 for expenses. How much rent must he charge (in dollars) for each of the 4 apartments if he wants to make $600 profit each month? The amount of rent is the same for each of the apartments.
Answers
Scott Mason is interested in making a $600 profit each month from his four-unit apartment building that he bought as an investment. The amount of rent for each of the four apartments will be the same. He currently pays out $500 for expenses monthly.
Therefore, the total amount of money he needs to make a month will be $500 + $600 = $1100. To determine how much rent he must charge, Scott must divide the total amount he needs by the number of apartments he has. Scott will have to make $1100 each month. Therefore, he must charge $1100 / 4 = $275 in rent for each of his four apartments. The amount of rent that Scott must charge for each apartment will be $275. This is calculated by adding the total amount of money he needs, which is $1100, and then dividing this amount by the number of apartments he has, which is 4. Therefore, each of the apartments will have to pay $275 in rent each month for Scott to make a profit of $600 each month.
To know more about apartments visit:
https://brainly.com/question/28718606
#SPJ11
\(2^{5} x 2^{3}\)
Answers
Answer:
2 5 x8
Step-by-step explanation:
i cant write it how it's supposed to be but u get it am sure its just 2 then 5 on top then just x8
sorry if i confused u hoped this helped..!!<3
![[tex]2^{5} x 2^{3}[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/8tUI5niGx7vAR6RZLVbU8mZmlIE86SQo.png)
What is x when f(x)=0?
Answers
Anything multiplied my 0 is indeed, 0. So f • 0 = 0.
Hope this helps! :D
Solve for the missing side or angle

Answers
The missing angle is 21.
In △ABC, ∠ABC = 60○
P is a point inside △ABC such that ∠APB = ∠BPC = ∠CPA, PA = 8, and PC = 6. Find PB.
Answers
A given shape that is bounded by three sides and has got three internal angles is referred to as a triangle. Thus the value of PB is 8.0 units.
A given shape that is bounded by three sides and has got three internal angles is referred to as a triangle. Types of triangles include right angle triangle, isosceles triangle, equilateral triangle, acute angle triangle, etc. The sum of the internal angles of any triangle is \(180^{o}\).
In the given question, point P is such that <APB = <APC = <BPC = \(120^{o}\). Also, line PB bisects <ABC into two equal measures. Thus;
<ABP = \(30^{o}\)
Thus,
<ABP + <APB + <BAP = \(180^{o}\)
30 + 120 + <BAP = \(180^{o}\)
<BAP = \(180^{o}\) - 150
<BAP = \(30^{o}\)
Apply the Sine rule to determine the value of PB, such that;
\(\frac{AP}{Sin B}\) = \(\frac{BP}{Sin30}\)
\(\frac{8}{Sin30}\) = \(\frac{BP}{Sin 30}\)
BP = \(\frac{8*Sin30}{Sin 30}\)
= \(\frac{4}{0.5}\)
BP = 8.0
Therefore, the value of BP = 8 units.
For more clarifications on applications of the Sine rule, visit: https://brainly.com/question/15018190
#SPJ1

What is the difference between a discrete
probability distribution and a continuous
probability distribution?
Give your own example of each. What is the
expected value, and what does it measure?
How is it computed for a discrete probability
distribution?
Answers
A discrete probability distribution is a statistical distribution that relates to a set of outcomes that can take on a countable number of values, whereas a continuous probability distribution is one that can take on any value within a given range.Therefore, the main difference between the two types of distributions is the type of outcomes that they apply to.
An example of a discrete probability distribution is the probability of getting a particular number when a dice is rolled. The possible outcomes are only the numbers one through six, and each outcome has an equal probability of 1/6. Another example is the probability of getting a certain number of heads when a coin is flipped several times.
On the other hand, an example of a continuous probability distribution is the distribution of heights of students in a school. Here, the range of heights is continuous, and it can take on any value within a given range.
The expected value of a probability distribution measures the central tendency or average of the distribution. In other words, it is the long-term average of the outcome that would be observed if the experiment was repeated many times.
For a discrete probability distribution, the expected value is computed by multiplying each outcome by its probability and then adding the results. In mathematical terms, this can be written as E(x) = Σ(xP(x)), where E(x) is the expected value, x is the possible outcome, and P(x) is the probability of that outcome.
For example, consider the probability distribution of the number of heads when a coin is flipped three times. The possible outcomes are 0, 1, 2, and 3 heads, with probabilities of 1/8, 3/8, 3/8, and 1/8, respectively. The expected value can be computed as E(x) = (0*1/8) + (1*3/8) + (2*3/8) + (3*1/8) = 1.5.
Therefore, the expected value of the distribution is 1.5, which means that if the experiment of flipping a coin three times is repeated many times, the long-term average number of heads observed will be 1.5.
express in two line copy(-2)×(+3)
(with photo)
Answers
Answer:
Step-by-step explanation:
The product of a negative two and a positive three is equal to negative six (-6).
