Answers
To find the x-intercept(s), we can use the quadratic formula:
\(x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}\)This formula is applied when we have a polynomial of the form:
\(ax^2+bx+c=0\)We have that our case is:
\(\frac{1}{4}x^2+\frac{3}{2}x-\frac{1}{8}=0\)To find the x-intercepts of the parabola. However, we can find the least common multiple of the denominators to have an easier equation to solve. Then, we have:
\(\operatorname{lcm}(4,2,8)=8\)Then, we can multiply each side of the equation by 8 as follows:
\(8(\frac{1}{4}x^2+\frac{3}{2}x-\frac{1}{8}=0)\)\(\frac{8}{4}x^2+\frac{8\cdot3}{2}x-\frac{8\cdot1}{8}=8\cdot0\Rightarrow2x^2+12x-1=0\)Now, we have that:
a = 2
b = 12
c = -1
Then, we have:
\(x=\frac{-12\pm\sqrt[]{12^2^{}-4(2)(-1)}}{2\cdot2}\)\(x=\frac{-12\pm\sqrt[]{144+8}}{4}\Rightarrow x=\frac{-12\pm\sqrt[]{152}}{4}\)Then
\(\sqrt[]{152}=\sqrt[]{2^2\cdot2\cdot19}=2\cdot\sqrt[]{38}\)Then, the two x-intercepts are:
\(x=\frac{-12\pm2\cdot\sqrt[]{38}}{4}\)\(x=\frac{-12+2\cdot\sqrt[]{38}}{4}\Rightarrow x=-\frac{12}{4}+\frac{2\cdot\sqrt[]{38}}{4}=-3+\frac{\sqrt[]{38}}{2}\)And
\(x=\frac{-12-2\cdot\sqrt[]{38}}{4}\Rightarrow x=-\frac{12}{4}-\frac{2\cdot\sqrt[]{38}}{4}=-3-\frac{\sqrt[]{38}}{2}\)Therefore:
The smallest x-intercept is:
\(-3-\frac{\sqrt[]{38}}{2}\)The largest x-intercept is:
\(-3+\frac{\sqrt[]{38}}{2}\)Finding the value of the vertex
To find the vertex of the parabola, we can find its x-value, and y-value using the following formulas:
\(x_v=-\frac{b}{2a},y_v=c-\frac{b^2}{4a}_{}\)In the original equation, we have:
a = 1/4
b = 3/2
c = -1/8
Then, we have:
\(x_v=-\frac{\frac{3}{2}}{2(\frac{1}{4})_{}}=-\frac{\frac{3}{2}}{\frac{2}{4}}=-\frac{3}{2}\frac{4}{2}=-\frac{3\cdot4}{4}\Rightarrow x_v=-3\)And
\(y_v=-\frac{1}{8}-\frac{(\frac{3}{2})^2}{4(\frac{1}{4})}=-\frac{1}{8}-\frac{\frac{9}{4}}{1}=-\frac{1}{8}-\frac{9}{4}=-(\frac{1}{8}+\frac{9}{4})=-(\frac{4+72}{32})\)Finally:
\(y_v=-\frac{76}{32}\Rightarrow y_v=-\frac{19}{8}\)Therefore, the vertex of the parabola is:
\((-3,-\frac{19}{8})\)In summary, we have:
The coordinates for the vertex are:
\((-3,-\frac{19}{8})\)The smallest x-intercept (only the
Related Questions
What is the first term of the quotient of the following division problem?
(x³ - 1) = (x + 2)
O -0.5
O 1
O x²
Ox^4
Answers
The solution to the algebraic problem is \(x^{2}\)
What is an Algebraic Equation?
An algebraic equation is a mathematical statement that sets two expressions equal to each other. An algebraic equation is typically made up of a variable, coefficients, and constants.
Solution:
(\(x^{3}\) – 1) = (x+2)
On dividing (\(x^{3} - 1\)) by (x+2)
The first term of the quotient will be x^2 by following the Long Division Method of Algebraic Division.
To learn more about Algebraic Equation from the given link
https://brainly.com/question/4541471
#SPJ9
How many solutions does this system of equations have y = -1/3x + 7. y = -2x^3 + 5x^2 + x - 2
Answers
The system of equations has one solution.
How many solutions does this system has?To check this, we can graph the two equations of the system:
y = (-1/3)x + 7
y = -2x³ + 5x² + x - 2
On the same coordinate axis, and check how many times do the graphs intercept.
The graph can be seen in the image at the end, there you can see that there is only one intecept point. Thus, the system of equations has only one solution.
Learn more about systems of equations at:
https://brainly.com/question/13729904
#SPJ1
A
X
Find the value of x.
D
X+2
x = [?]
B
3
E
2
C
![AXFind the value of x.DX+2x = [?]B3E2C](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/NizqkSoyno5R9ihZJuX6BBJHmDyqL8LN.png)
Answers
Answer:
x = 4
Step-by-step explanation:
if a line is parallel to a side of a triangle and it intersects the other two sides then id divides those sides proportionally.
DE is such a line , then
\(\frac{BD}{AD}\) = \(\frac{BE}{EC}\) ( substitute values )
\(\frac{x+2}{x}\) = \(\frac{3}{2}\) ( cross- multiply )
3x = 2(x + 2)
3x = 2x + 4 ( subtract 2x from both sides )
x = 4
Consider matrix A.
What matrix results from the elementary row operations represented by −2R2+3R1?
Answers
Answer:
\(A = \left[\begin{array}{ccc}-3&3&2\\-25&-13&0\end{array}\right]\)
Step-by-step explanation:
Given the matrix
\(A = \left[\begin{array}{ccc}-3&3&2\\8&-1&3\end{array}\right] \\R1 = -3, 5, 2\\R2 = 8, -1, 3\\\\\)
Before we can get the resulting matrix after the elementary operation, we need to get the new second row using the formula −2R2+3R1?
when R1= -3, R2 = 8
−2R2+3R1? = −2(8)+3(-3)
−2(8)+3(-3) = -16-9
−2(8)+3(-3) = -25
R1= 5, R2 = -1
−2R2+3R1? = −2(-1)+3(5)
−2(-1)+3(5) = 2-15
−2(-1)+3(5) = -13
when R1= 2, R2 = 3
−2R2+3R1? = −2(3)+3(2)
−2(3)+3(2) = -6-6
−2(3)+3(2) = 0
Hence the new R2 are -25, -13, 0
The resulting matrix will be:
\(A = \left[\begin{array}{ccc}-3&3&2\\-25&-13&0\end{array}\right]\)
Answer:
-25 17 0
8 -1 3
Step-by-step explanation:
a set of average city temperatures in december are normally distributed with a mean of 16.3°C and a standard deviation of 2°C. what proportion of temperatures are between 12.9°C and 14.9°C?
Answers
Answer:
19.74% of temperatures are between 12.9°C and 14.9°C
Step-by-step explanation:
Problems of normally distributed samples are solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
In this question, we have that:
\(\mu = 16.3, \sigma = 2\)
What proportion of temperatures are between 12.9°C and 14.9°C?
This is the pvalue of Z when X = 14.9 subtracted by the pvalue of Z when X = 12.9.
X = 14.9
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{14.9 - 16.3}{2}\)
\(Z = -0.7\)
\(Z = -0.7\) has a pvalue of 0.2420
X = 12.9
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{12.9 - 16.3}{2}\)
\(Z = -1.7\)
\(Z = -1.7\) has a pvalue of 0.0446
0.2420 - 0.0446 = 0.1974
19.74% of temperatures are between 12.9°C and 14.9°C
The value of X is _____.
Answers
Answer:
96
Step-by-step explanation:
The sum of the external angles of any convex polygon is 360°. Then the value of x° is ...
x° = 360° -130° -134°
x° = 96°
The value of x is 96.
if h(x) is the inverse of f(x), what is the value of h(f(x))?01xf(x)
Answers
From the given question:
If h(x) is the inverse of f(x), then the value of h(f(x)) will be x
For example:
\(\begin{gathered} f(x)=3x+4 \\ h(x)=\frac{x-4}{3} \\ h(f(x))=h(3x+4) \\ =\frac{(3x+4-4)}{3} \\ =\frac{3x}{3} \\ =x \end{gathered}\)Hence, the correct option is C.
Amadi has jar with one dollar and two dollar coins in it.
There are coins in total.
A jar of one and two dollar coins.
The ratio of one dollar coins to two dollar coins is .
How many coins are two dollar coins
Answers
Without knowing the total number of coins or the ratio between one dollar and two dollar coins in the jar, we cannot accurately determine the number of two dollar coins.
Amadi has a jar with both one dollar and two dollar coins. The question is asking how many of the coins in the jar are two dollar coins.
To determine the number of two dollar coins, we need more information. The question does not provide any details about the total number of coins or the ratio between one dollar and two dollar coins in the jar. Without this information, it is not possible to give an accurate answer.
If we assume that the jar contains a total of 100 coins, we can use algebra to solve for the number of two dollar coins.
Let's say the number of two dollar coins is x. Then, the number of one dollar coins would be 100 - x.
Since the value of the two dollar coins is double the value of the one dollar coins, we can set up the equation 2x + 1(100 - x) = total value of coins.
Simplifying the equation, we get 2x + 100 - x = total value of coins.
Combining like terms, we have x + 100 = total value of coins.
Since we don't know the total value of coins, we cannot solve for x. Therefore, we cannot determine the number of two dollar coins without additional information.
For more such questions on dollar
https://brainly.com/question/30057220
#SPJ8
2/5 divided by 3/5 in simplest form
Answers
Answer:
2/3
Step-by-step explanation:
Extending so that I can send.
Answer:
2/3
Step-by-step explanation:
The product of two numbers is 155952. If one number is 342, find the other
number.
Answers
Answer:
456
Step-by-step explanation:
Product means an answer derived from multiplication. Therefore, if the product is 155952, and one value is 342, then the following equation is true:
342x = 155952, or 342 * x = 155952
Divide 155952 by 342 to get: 456.
Check the work in the equation:
342(456) = 155952
155952 = 155952, which is true, so the answer is 456.
If I helped, please make this answer brainliest! ;)
1. If <1 is 120 degrees , what is the measure of <2?
Answers
Answer:
240
Step-by-step explanation:
2 is 1 + 1 so 120 + 120 must be the equivalent of 2.
If the triangles third vertex has a coordinate (0,y) which is possible value of Y
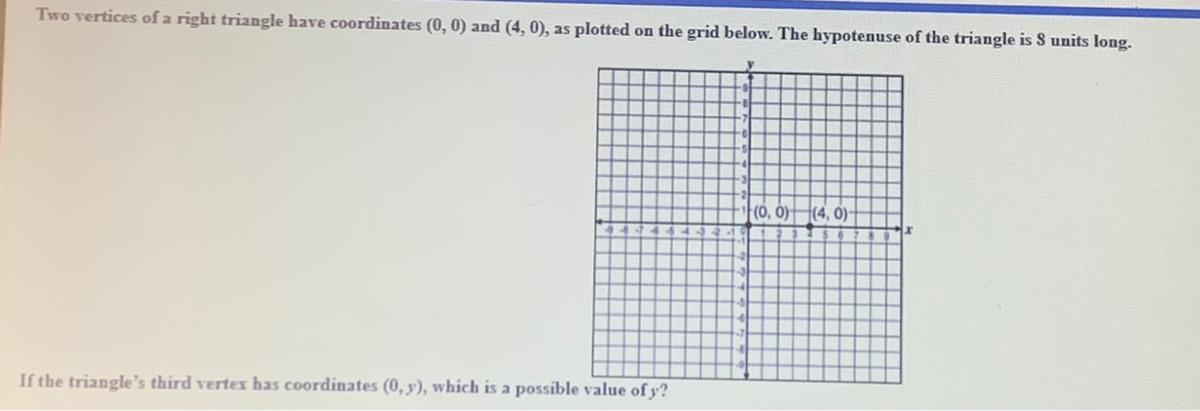
Answers
Explanation
the coordinate (0,y) makes a triangle
then
\(\begin{gathered} \text{hypotenuse}=8 \\ \text{side}_1=\Delta x=4-0=4 \\ \text{side}_{2_{}}=\Delta y=y-0=y \end{gathered}\)now, we can use the Pythagorean theorem to find y. P.T states that the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse,so in this case.
\(\text{side}^2_1+side^2_2=hypotenuse^2\)replace.
\(\begin{gathered} \text{side}^2_1+side^2_2=hypotenuse^2 \\ 4^2+y^2=8^2 \\ 16+y^2=64 \\ y^2=64-16(\text{subtract 16 in both sides)} \\ y^2=48 \\ \text{square root in both sides} \\ y=\sqrt[]{48} \\ \text{apply properties of the root} \\ y=\sqrt[]{16\cdot3} \\ y=\sqrt[]{16}\cdot\sqrt[]{3} \\ y=4\sqrt[]{3} \end{gathered}\)therefore, a posible value for y is
\(y=4\sqrt[]{3}\)I hope this helps you
What is the vertical displacement of the basic graph to produce a graph of
OA Sunits down
B. 2 units down
OC units down
OD
units up
SUBMIT
Answers
The vertical displacement is of 2 units down, the correct option is B.
What is the vertical displacement?Remember that for a function f(x), a vertical displacement of N units is written in general form as:
g(x) = f(x) + N
If N > 0, the translation is upwards.
if N < 0, the translation is downwards.
Here we assume that we start with the parent cosine function:
y = cos(x)
And the transformed function is:
y = -2 - cos(x - π)
So we have some transformations, but the vertical translation is of 2 units down. So the correct option is B.
Learn more about translations at:
https://brainly.com/question/24850937
#SPJ1
Trevor sees 8 red birds. He sees 5 more red birds than blue birds. How many blue birds Trevor see?
Answers
Will give Brainly if correct
Answers
Answer: -8
Step-by-step explanation: When it says f(x), all you have to do is find value x on the coordinate plane and look up or down until you find a point that runs through that x value. In this case, if you draw a line on x=5, you can see that it goes across a point that has a y value of -8, which is your answer.
A llne passes through the two glven points. Is it vertical, horizontal, or neither?
(1, 0), (0, 0)
O Vertical
Horizontal
Neither
Answers
Answer:
Horizontal: if y is equal to 0, then there is no vertical movement
4. Find the sum of the first 21 terms in a series where a = 20 and t21= 400.
5. Find the sum of the first 100 terms in a series where a = 0 and t100= 99.
6. Find the sum of the first 50 terms in a series where a = 4 and t50= 196.
7. Find the sum of the first 100 terms in a series where a = 0 and t100= 99.
8. Find the sum of the first 10 terms in an arithmetic series where t7= 7 and t10= 13.
9. Find the sum of the first 10 terms in an arithmetic series where t5= 15 and t10= 45.
10. Find the sum of the first 30 positive multiples of 5.
Answers
The first 100 terms of a series add up to 4950, and the first 21 terms of a series where a = 20 and t21 = 400 add up to 4410
what is arithmetic progression ?An arithmetic progression is when the difference between each phrase that follows another in a sequence is always the same. For instance, the sequence 5, 7, 9, 11, 13, and 15 is an example of an arithmetic progression with a 2 tolerance. A progression having a set tolerance between any two consecutive numbers is known as a "arithmetic progression" (A.P.). Two alternative types of mathematical progression exist: finite-length mathematical series A series that has a limited number of terms is a finite geometric progression. One may calculate the early, late, tolerance, and number of terms in a series using the terms in the series.
given
1) n6 = 6 where a = 5 and d = 5 = 105
2)n6 =6 where a = 9 and d = 12 = 234
3) n5= 5 where a = 5.7 and d = 1.4 = 42.5
4) a = 20 and t₂₁ = 400 ,
= 380
Therefore, Sum of 21 terms = 4410
5) In series a = 0 and t₁₀₀ = 99 = 4950
The first 100 terms of a series add up to 4950, and the first 21 terms of a series where a = 20 and t21 = 400 add up to 4410
To know more about arithmetic progression visit:
https://brainly.com/question/16947807
#SPJ1
please please please
Answers
Answer:
don't give up try and you will find the answers
4x+5(7x-3)=9(x-5)
x????
Answers
Answer:
x=-1
Step-by-step explanation:
4x+35x-15=9x-45
39x-15=9x-45
39x-9x=-45+15
30=+-30
x=-1
Answer:
\( \sf \: x = - 1\)
Step-by-step explanation:
Given equation,
→ 4x + 5(7x - 3) = 9(x - 5)
Now the value of x will be,
→ 4x + 5(7x - 3) = 9(x - 5)
→ 4x + 35x - 15 = 9x - 45
→ 39x - 15 = 9x - 45
→ 39x - 9x = -45 + 15
→ 30x = -30
→ x = -30 ÷ 30
→ [ x = -1 ]
Hence, the value of x is -1.
Question 10 of 25 What is the recursive formula for this geometric sequence? -2,-16, -128, -1024,... A. ○ B. C. (a, D. 3₁ = :-2 an = 2n-1 = = -2 an = an-1.8 • a₁ = 8 an = an-1• (-2) (a₁ = -8 30 = 20-1.2 SUBMIT
Answers
Answer:
\(a_{n}\) = 8\(a_{n-1}\) ; a₁ = - 2
Step-by-step explanation:
a recursive formula in a geometric sequence allows a term to be found by multiplying the preceding term by the common ratio r
here r = \(\frac{a_{2} }{a_{1} }\) = \(\frac{-16}{-2}\) = 8 , then
\(a_{n}\) = 8\(a_{n-1}\) ; a₁ = - 2
20ft flag pole has a rope tied from to top to the ground. The rope makes a 35° angle with the ground. How long is the rope?
Answers
the length of the rope is approximately 11.9 feet.
What is right angle triangle?
The term "right-angled triangle" refers to any triangle with an internal angle that is either a right angle or 90 degrees in value. The right triangle or the 90-degree triangle are other names for this triangle because of this. Right triangles have "opposite" and "adjacent" sides, which refer to the sides that are across from and next to respective angles, respectively. When a right triangle is formed, the hypotenuse is its longest side.
We can consider the flagpole, the ground, and the rope as forming a right triangle. The angle between the flagpole and the rope is 90 degrees, and the angle between the rope and the ground is 35 degrees. Therefore, the angle between the flagpole and the ground is 90 - 35 = 55 degrees.
Let's call the length of the rope "r". We can use the trigonometric function tangent to find r:
tan(35°) = opposite/adjacent = r/20
Multiplying both sides by 20, we get:
r = 20 tan(35°)
Using a calculator, we get:
r ≈ 11.9 feet
Therefore, the length of the rope is approximately 11.9 feet.
Learn more about right angle triangle, by the following link
https://brainly.com/question/64787
#SPJ1
Kayla walks 4 2/5 miles each day. How far does she walk?
Answers
A population numbers 12,000 organisms initially and grows by 17.5% each year.
Suppose P represents population, and t the number of years of growth. An exponential model for the population can be written in the form P = a â‹… b t where
P =
Answers
A population numbers 12,000 organisms initially and grows by 17.5% each year. The growth function of the population is P = 12,000 x 1.175^t
An exponential growth function can be written as:
P = A (1 + r)ⁿ
Where:
P = quantity after n periods
n = number of periods
r = growth rate per period
A = initial quantity
In the given problem, the period is the number of years t
A = 12,000
r = 17.5% = 0.175
Hence, the growth function:
P = 12,000 (1 + 0.175)^t
P = 12,000 x 1.175^t
Your question is incomplete, but most probably your question was:
A population numbers 12,000 organisms initially and grows by 17.5% each year. Suppose P represents population, and t the number of years of growth, write the function in terms of t.
Learn more about growth model here:
https://brainly.com/question/20291621
#SPJ4
PLSS HELP
GIVING 36 POINTS
Answers
Answer:
a
Step-by-step explanation:
the data is represented in the dot plot
Answer:
answer is 77.67
Step-by-step explanation:
explain by the x axis is 68 to y axis is 84 so the median is 77.67
what is the property of 3x(5x7)=(3x5)7
Answers
The property you are referring to is called the associative property of multiplication. According to this property, when multiplying three numbers, the grouping of the numbers does not affect the result. In other words, you can change the grouping of the factors without changing the product.
In the equation you provided: 3x(5x7) = (3x5)7
The associative property allows us to group the factors in different ways without changing the result. So, whether we multiply 5 and 7 first, or multiply 3 and 5 first, the final product will be the same.
Use the Distributive Property to rewrite the algebraic expression.
7(x + 2) (I will give brainliest)
Answers
Answer:
7x+14
Step-by-step explanation:
7 times x = 7x
7 times 2 = 14
put it together 7x+14
Answer:
7x+14
you multiply 7 by x and 2
A diving board is 12.4 feet above the ground. The bottom of the pool is 16.9 feet below the ground. Use the equation from the previous question to solve the equation. Circle your answer
Answers
Answer:
12.4+16.9= 29.3 feet
Step-by-step explanation:
hope this helps
Graph the equation −3x+5y=7 by plotting points using the line tool.
Answers
A graph of the linear equation -3x + 5y = 7 in slope-intercept form is shown in the image attached below.
What is a graph?In Mathematics, a graph is a type of chart that is typically used for the graphical representation of data points or ordered pairs on both the horizontal and vertical lines of a cartesian coordinate respectively.
Next, we would rearrange and simplify the given given linear equation in slope-intercept form in order to enable us plot it on a graph:
-3x + 5y = 7
5y = 3x + 7
y = 3x/5 + 7/5
Lastly, we would use an online graphing calculator to plot the given function as shown in the graph attached below.
In conclusion, the slope of this linear equation is equal to 3/5 and it does not represent a proportional relationship.
Read more on a graph here: brainly.com/question/4546414
#SPJ1
the temperature is -56F. How many degreees below zero is the temperature?
Answers
The number of degrees below zero is given by A = 56° F
What is Modulus Function?Regardless of the sign, a modulus function returns the magnitude of a number. The absolute value function is another name for it.
It always gives a non-negative value of any number or variable. Modulus function is denoted as y = |x| or f(x) = |x|, where f: R → (0,∞) and x ∈ R.
The value of the modulus function is always non-negative. If f(x) is a modulus function , then we have:
If x is positive, then f(x) = x
If x = 0, then f(x) = 0
If x < 0, then f(x) = -x
Given data ,
Let the initial temperature be represented as T
Let the number of degrees below zero be A
Now , the value of T is
T = -56° F
From the modulus function , we get
The value of the modulus function is always non-negative.
So , the measure of A = | T |
A = | -56 |
A = 56° F
Hence , the number of degrees below zero is 56° F
To learn more about modulus function click :
https://brainly.com/question/13682596
#SPJ9
Prove the Converse of the Pythagorean Theorem
In this activity, you will prove and apply the converse of the Pythagorean theorem. Recall that the
converse states that if the square of the length of the longest side of a triangle is equal to the sum of
the squares of the other two sides, then the triangle is a right triangle.
Open the GeoGebra activity to complete each step below. For help, watch these short videos about
using GeoGebra to measure and create points, lines, and anglese.
Question 1
Part A
Draw AABC with vertices at A(1,6), B(1, 1) and C(5,1). In this triangle, AB²+ BC² = AC².
Next, use the GeoGebra tools to draw ADEF such that AB = DE, m/E
Paste a picture of your drawing in the answer box.
= 90°, and EF
BC.
B I U X² X2 15px
AVA
E E g = = 三 四 V 田
=
Answers
The based on this example, we can see that the converse of the Pythagorean theorem does not hold for this particular triangle.
To prove the converse of the Pythagorean theorem, we need to show that if the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.
In the given triangle AABC, with vertices at A(1,6), B(1,1), and C(5,1), we can calculate the lengths of the sides using the distance formula or Pythagorean theorem.
AB = sqrt((1-1)^2 + (6-1)^2) = sqrt(25) = 5
BC = sqrt((5-1)^2 + (1-1)^2) = sqrt(16) = 4
AC = sqrt((5-1)^2 + (6-1)^2) = sqrt(40) = 2sqrt(10)
Now, let's check if AB^2 + BC^2 = AC^2:
AB^2 + BC^2 = 5^2 + 4^2 = 25 + 16 = 41
AC^2 = (2sqrt(10))^2 = 4(10) = 40
Since AB^2 + BC^2 is not equal to AC^2, the given triangle AABC does not satisfy the condition for the converse of the Pythagorean theorem.
For more such questions on Pythagorean theorem:
https://brainly.com/question/28981380
#SPJ8