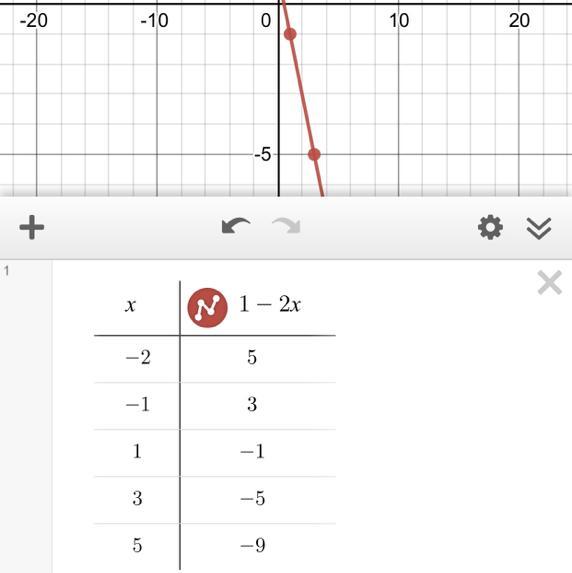
Using y = 1 − 2x, plot the ordered pairs from the table. Then graph the function represented by the ordered pairs and tell whether the function is linear or nonlinear.
Helppp plzz due in 20 min

Answers
Related Questions
Point A is at-4 and point B is at 6. Which describes one way to find the point that divides AB into a 3:2 ratio?
A
B
-5-4-3 -2 -1 0 1 2 3 4 5 6 7 8
O For a ratio of 3:2, divide AB into 3 equal parts. Each equal part is 3 units, so the point that divides AB into a 3:2
ratio is 0.
O For a ratio of 3:2, divide AB into 3 equal parts. Each equal part is 3 units, so the point that divides AB into a
3:2 ratio is 3.
O For a ratio of 3:2, divide AB into 5 equal parts. Each equal part is 2 units, so the point that divides AB into a
3:2 ratio is 1.
O For a ratio of 3:2, divide AB into 5 equal parts. Each equal part is 2 units, so the point that divides AB into a
3:2 ratio is 2.
Answers
Each equal part is 2 units, so the point that divides AB into a 3:2 ratio is 2. Therefore, option D is correct.
Given that the point A is at -4 and the point B is at 6.
We need to find the point that divides AB into a 3:2 ratio.
One way to find the point that divides AB into a 3:2 ratio is to divide AB into 5 equal parts.
Each equal part is 2 units, so the point that divides AB into a 3:2 ratio is 2.
Therefore, option D is correct.
Option A is incorrect because the point that divides AB into a 3:2 ratio is not 0.Option B is incorrect because the point that divides AB into a 3:2 ratio is not 3.Option C is incorrect because the point that divides AB into a 3:2 ratio is not 1.
For more such questions on divides , Visit:
https://brainly.com/question/30126004
#SPJ8
10005²³ x + cos x = 11 sin²x = 9
Answers
a) What is the area of the top face of this
cuboid?
b) What is the area of the bottom face of
this cuboid?
4 cm
9 cm
7 cm
Answers
The area of both the top face and the bottom face of the cuboid is 63 square centimeters (cm²).
To find the area of each face of the cuboid, we'll use the formulas for finding the area of a rectangle (which is the shape of each face of the cuboid).
Given dimensions:
Length (L) = 9 cm
Width (W) = 7 cm
Height (H) = 4 cm
a) Area of the top face of the cuboid:
The top face is a rectangle with dimensions 9 cm (length) and 7 cm (width).
Area = Length × Width
Area = 9 cm × 7 cm
Area = 63 square centimeters (cm²)
b) Area of the bottom face of the cuboid:
The bottom face is also a rectangle with dimensions 9 cm (length) and 7 cm (width).
Area = Length × Width
Area = 9 cm × 7 cm
Area = 63 square centimeters (cm²)
Therefore, the area of both the top face and the bottom face of the cuboid is 63 square centimeters (cm²).
To know more about cuboid here
https://brainly.com/question/26403859
#SPJ2
Felipe pays $1.50 per carton for fresh eggs from the farmers market and $2 for a water. If Felipe spends a total of $9.50, how many cartons of eggs did he buy
Answers
Answer:
7.50
Step-by-step explanation:
i'm dumb
Answer:
He can buy 5 cartons of eggs
Step-by-step explanation:
Take $9.50 and subtract $2
Then divide that answer by $1.50
2x1+0x2+3x3=3
4x1-3x2+7x3=5
8x1-9x2+15x3=10
solve the system using Gaussian or Gauss-Jordan elimination
Answers
[1] … … 2x₁ + 0x₂ + 3x₃ = 3
[2] … … 4x₁ - 3x₂ + 7x₃ = 5
[3] … … 8x₁ - 9x₂ + 15x₃ = 10
Since [1] is already free of x₂, you might as well start by eliminating x₂ from the other two equations. Add -3 times [2] to [3] :
-3 (4x₁ - 3x₂ + 7x₃) + (8x₁ - 9x₂ + 15x₃) = -3 (5) + 10
-12x₁ + 9x₂ - 21x₃ + 8x₁ - 9x₂ + 15x₃ = -15 + 10
-4x₁ - 6x₃ = -5
[4] … … 4x₁ + 6x₃ = 5
Now eliminate x₃ in [1] and [4]. Add -2 times [1] to [4] :
-2 (2x₁ + 3x₃) + (4x₁ + 6x₃) = -2 (3) + 5
-4x₁ - 6x₃ + 4x₁ + 6x₃ = -6 + 5
0 = -1
which is a contradiction. This means the system has no solution.
Which statements are true for solving the equation 0.5 – |x – 12| = –0.25? Check all that apply.
The equation will have no solutions.
A good first step for solving the equation is to subtract 0.5 from both sides of the equation.
A good first step for solving the equation is to split it into a positive case and a negative case.
The positive case of this equation is 0.5 – |x – 12| = 0.25.
The negative case of this equation is x – 12 = –0.75.
The equation will have only 1 solution
Answers
The true statement is:
"A good first step for solving the equation is to subtract 0.5 from both sides of the equation."
Which statements are true for solving the equation?We have the absolute value equation:
0.5 - |x - 12| = 0.25
Now, if we subtract 0.5 from both sides, we get:
-|x - 12| = 0.25 - 0.5 = -0.25
Now we can multiply both sides by -1 to get:
|x - 12| = 0.25
Now we need to split in the negative and positive parts:
x - 12 = 0.25
x - 12 = -0.25
And now we can solve these two to get the two solutions:
x = 0.25 + 12 = 12.25x = -0.25 +12 = 11.75Now that we performed the whole solution, the statement that is true is:
"A good first step for solving the equation is to subtract 0.5 from both sides of the equation."
Al the other ones are false.
If you want to learn more about absolute value equations:
https://brainly.com/question/1622683
#SPJ1
Answer:
For edge the answer is b and e
Step-by-step explanation:
Simplify the intersection(-∞, -7] ∩ [-7,9)How to solve
Answers
The intersection of sets for two given sets is the set that contains all the elements that are common to both sets. The symbol for intersection of sets is "∩"
In this instance, ( -∞, -7] ∩ [-7,9) is -7, since only -7 is both common on both sets.
I don’t know the answer please help me out

Answers
Explanation:
1/3 x 45 is 15, so the comparison is correct because 15 is less than 45.
the rest of the choices are incorrect because:
B. 60 < 60 x 3/4 is wrong because 60 x 3/4 = 45 which is LESS than 60, not greater
C. 20 x 1/5 >20 is wrong because 20 x 1/5 = 4 which is LESS than 20, not greater
D. 25 < 2/3 x 25 is wrong because 2/3 x 25 = 16 2/3 which is LESS than 25, not greater
Have a nice day (brainliest pls tysm!)
I don’t understand this question.

Answers
Answer:
-7.89 is the answer
mark me the brainlets
Step-by-step explanation:
graph h(x)=(x-1)^2-9
Answers
The graph of h(x) = (x-1)^2 - 9 is a U-shaped parabola that opens upwards, with the vertex at (1, -9), and it extends indefinitely in both directions.
The function h(x) = (x-1)^2 - 9 represents a quadratic equation. Let's analyze the different components of the equation to understand the behavior of the graph.
The term (x-1)^2 represents a quadratic term. It indicates that the graph will have a parabolic shape. The coefficient in front of the quadratic term (1) implies that the parabola opens upwards.
The constant term -9 shifts the graph downward by 9 units. This means the vertex of the parabola will be at the point (1, -9).
Based on this information, we can draw the following conclusions:
The graph will be a U-shaped curve with the vertex at (1, -9).
The vertex represents the minimum point of the parabola since it opens upward.
The parabola will be symmetric with respect to the vertical line x = 1 since the coefficient of the quadratic term is positive.
The graph will extend indefinitely in both directions.
To accurately plot the graph, you can choose several x-values, substitute them into the equation to find the corresponding y-values, and then plot the points on the graph. Alternatively, you can use graphing software or calculators that can plot the graph of the equation for you.
Remember to label the axes and indicate the vertex at (1, -9) to provide a complete representation of the graph of h(x) = (x-1)^2 - 9.
for such more question on parabola
https://brainly.com/question/9201543
#SPJ8
TIME REMAINING
01:48:30
On a coordinate plane, 2 lines are shown. Line H J has points (negative 4, negative 2) and (0, 4). Line F G has points (negative 4, 1) and (0, negative 2).
Which statement best explains the relationship between lines FG and HJ?
They are perpendicular because their slopes are equal.
They are perpendicular because their slopes are negative reciprocals.
They are not perpendicular because their slopes are equal.
They are not perpendicular because their slopes are not negative reciprocals.
Answers
Answer:
Its b i bealive
Step-by-step explanation:
!!MATH!! !!100 POINTS!! !!WILL MARK BRAINLIEST!!

Answers
Answer:
PQO = 180
OQR = 180
PQR = 220
Step-by-step explanation:
brainliest
A rule for creating a pattern is given below. The rule begins with a number called the input and creates a number called the output. Rule: Multiply the input by 6 to get the output. Which input and output table works for the rule? Choose 1 answer:
Answers
2 is the input value, while 6 is the result.
We know the rule is Multiply the input by 6 to get the output.
= (2*5)-4
=10-4
=6.
A function rule is the equation-based relationship between dependent and independent variables. How to calculate the value of the dependent variable, say y, in terms of the independent variable, say x, is explained by the function rule of a particular function. A function table includes a function rule as well as input and output values. If we plug in various values for the input, we obtain corresponding values of output according to the function rule. The relationship between the input values x and the output values y always follows a pattern that is specified by the function rule.
Hence, the input and output value of a table is 2 and 6.
To know more about Input and output rule, visit:
brainly.com/question/28352674
#SPJ1
A passenger car will go 444 miles on 18.5 gallons of gasoline in city drinking. what's the rate in miles per gallon.
Answers
In order to calculate the rate in miles per gallon, we just have to divide the given distance ( 444 miles) by the gallons (18.5 gallons), then we get:
rate in in miles per gallon = 444 miles/18.5 gallons = 24 miles/galons
Then, the rate in miles per gallon is 24 miles/galons
Need Help please, here is screenshot

Answers
1)
The axis of symmetry is x = -6.
2)
Vertex is (-6, 26).
3)
f(x) has a maximum value.
4)
f(x) is concave down.
What is an equation?An equation is a mathematical statement that is made up of two expressions connected by an equal sign.
Example:
2x + 3 = 7 is an equation.
We have,
f(x) = -x² - 12x - 10
This is in the form of ax² + bx + c.
a = -1, b = -12, c = -10
The axis of symmetry is x = -b/2a
x = 12/(-2)
x = -6
Now,
f(x) = -x² - 12x - 10
f(x) = -(x² + 12x + 10)
f(x) = - { (x² + 12x + 36) - 36 + 10}
f(x) = -(x + 6)² + 26
This is in the form of f(x) = a (x - h)² + k
a = -1, h = -6, k = 26
Vertex = (h, k) = (-6, 26)
Now,
f(x) = -x² - 12x - 10
f'(x) = -2x - 12
f''(x) = -2
It is a negative value.
This means f(x) has a maximum value.
Now,
From the graph, we see that f(x) is concave down.
Learn more about equations here:
https://brainly.com/question/17194269
#SPJ1

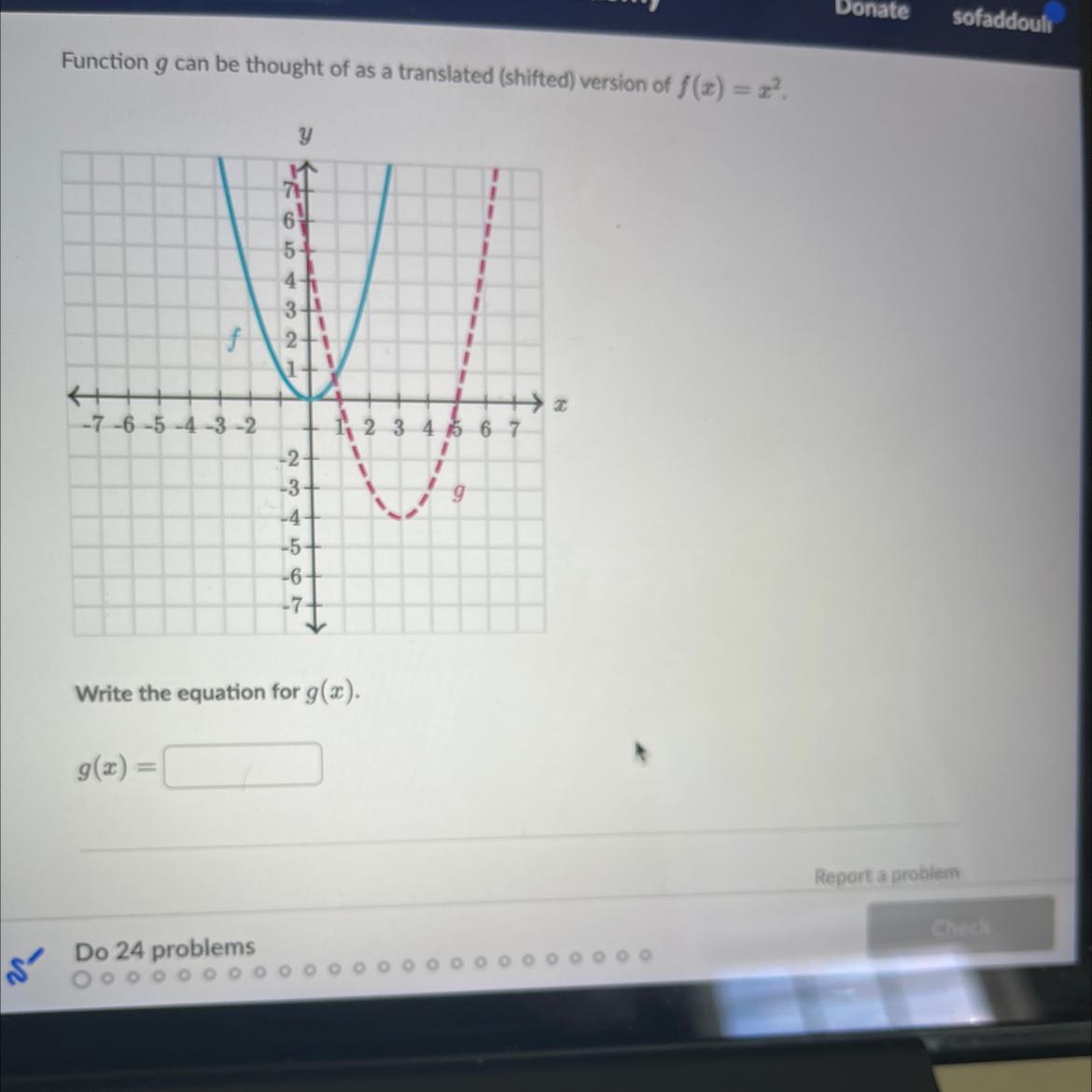
I need to know how to format a function equation after it has been translated
Answers
Given:
We're given the graph of f(x) = x²
If 3 paintings cost $30, then how much does 1 painting cost?
Answers
Answer:
10$
Step-by-step explanation:
because 10$ + 10$ + 10$ equals 30$ so one is 30$
I GIVE BRAINLIEST FOR EXPLANATION AND CORRECT ANSWER EXTRA POINTS 3

Answers
Answer:
\(x=8\)
Step-by-step explanation:
The best way to go about this is to use a trig identity. You have the unknown opposite the angle and the hypotenuse, so its best to use the sine identity: \(sin(x)=\frac{O}{H}\), where O is the opposite side, and H is the hypotenuse.
Set up the equation as:\(sin(27)=\frac{x}{17}\), and solve for X.
I got x=7.718, rounded to x=8.
If I helped, a brainliest answer would be greatly appreciated!
Ejemplo: catalina compro una piscina para
ponerla en el jardín de su casa.
-Piscina cilíndrica 206cm de diámetro y 60cm
de profundidad además construirá una zona de
cemento y cerco de seguridad alrededor de la
piscina.
¿Cuál es el volumen máximo de agua que
puede contener la piscina? (considere T=3)
¿cuál es la extensión del cerco de seguridad?
(considere П=3)
Answers
The length of the fence must be 618cm
The volume that it can hold is 1,909,620 cm³
How to find the volume and the length of the fence?First, the fence is just equal to the circumference of the cylinder, remember that the circumfernce of a circle of diameter D is:
C = П*D
Here we use П = 3, then:
C = П*206cm
C = 3*206cm = 618cm
Now the volume, for a cylinder of diameter D and height H, the volume is:
V = П*(D/2)²*H
Replacing the values that we know we will get:
V = 3*(206cm/2)²*60cm = 1,909,620 cm³
Learn more about cylinders at:
https://brainly.com/question/9554871
#SPJ1
Logan walks his dog every day. They walk by the river 5 days a week and they walk around the block two days a week. When they walk by the river, they see a dog 85% of the time. When they walk around the block, they see other dogs 30% of the time. Determine the probability that Logan and his dog will see another dog on their walk tomorrow. Hint: Draw a tree diagram to represent this situation. (Which way do they walk? Do they see a dog?)
Answers
The probabilities of walking tomorrow by the river and the block are 5/7 and 2/7, respectively. On the other hand, the probabilities of seeing another dog by the river and the block are 0.85 and 0.3, respectively.
Therefore,
\(P(anotherDog)=\frac{5}{7}\cdot0.85+\frac{2}{7}\cdot0.3=\frac{97}{140}\approx0.693\)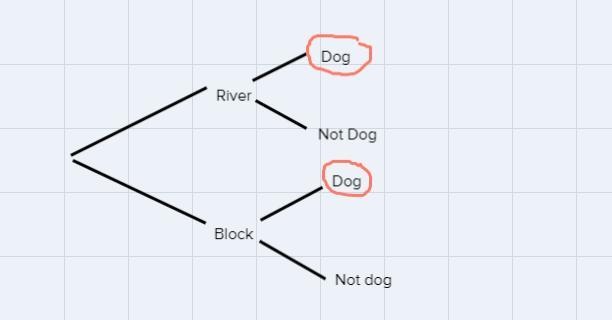
Magan went shopping for a new camera because of a sale. The price on the tag was $21, but Magan paid $12.60 before tax. Find the percent discount.
Answers
Answer:
40%
Step-by-step explanation:
To find the percent discount, take the original price and subtract the discounted price.
21 - 12.60=8.4
Divide this by the original price.
8.4/21 = .4
Change this to percent form.
.4 = 40%
Answer:
8.4
Step-by-step explanation:
The price of a bag = 21
Magan paid 12.60
00. 21
12.00
- - - - - - - - -
8.4
Suppose sam deposited 1000$ every month in the beginning for his retirement fund for 20 years at 5% compounded monthly. What is value of N
Answers
To find the value of N, we need the future value of the retirement fund. If you provide the desired future value, I can calculate the exact value of N.
To find the value of N, we need to calculate the number of monthly deposits Sam made for his retirement fund over 20 years.
Sam deposited $1000 every month for 20 years, which is a total of 20 x 12 = 240 deposits. Each deposit has a compounded interest rate of 5% per year, compounded monthly.
The formula to calculate the future value of a series of monthly deposits is given by:
FV = P * [(1 + r)^n - 1] / r
Where:
FV is the future value of the investment,
P is the monthly deposit amount,
r is the monthly interest rate, and
n is the number of deposits.
In this case, P = $1000, r = 5% / 12 = 0.05 / 12 = 0.00417 (monthly interest rate), and FV is the value of the retirement fund after 20 years.
By rearranging the formula, we can solve for n:
n = log((FV * r) / (P * r + FV)) / log(1 + r)
Plugging in the values, we get:
n = log((FV * 0.00417) / (1000 * 0.00417 + FV)) / log(1 + 0.00417)
For more such questions on future value
https://brainly.com/question/24703884
#SPJ8
Fill in the blank for this question!

Answers
While an absolute value may be any number, the output from an absolute value expression is always greater than or equal to zero
How to Interpret an Absolute Value Function?The absolute value | x | of a real number x is defined as the non-negative value of x without regard to its sign. For example, the absolute value of 3 is 3, and the absolute value of −3 is also 3. The absolute value of a number may be thought of as its distance from zero along real number line.
The absolute value of any number is seen to be always greater than or equal to zero. Both a number and its opposite are the same distance from zero on the number line. Since they have the same distance from zero, they have the same absolute value.
Read more about Absolute Value Function at: https://brainly.com/question/3381225
#SPJ1
Find the probability that a randomly
selected point within the square falls in the
red-shaded circle.
6
18
18
P =

Answers
The probability of landing on the red shaded circle is 6/18
Concept of probabilityProbability simply measures the chances at which an event could occur in a sample or population.
Mathematically, Probability is calculated thus:
P(X) = required outcome/ Total possible outcomesHere ,
Required = red circle = 6Entire circle = 18P(red circle ) = 6/18
Therefore, the probability is 6/18
Learn more on probability:https://brainly.com/question/24756209
#SPJ1
10 cm
a
6 cm
What is the length of the missing leg?
a =
centimeters
Answers
Answer:
10×6
= 60
Step-by-step explanation:
maaf kalau salah
Given the two rectangles below. Find the area of the shaded region.

Answers
Answer:
The area of the shaded region is 36.
Step-by-step explanation:
First, let's find the area of the rectangle as a whole, which will be 5*10 = 50. How did we get 50? The right side is 5 (from 2+3), and the top is 10 (3+7). Multiplying those numbers together will give you the area.
Now, the problem asks to find the shaded region. Let's solve for the area of the non-shaded region: (7*2) = 14.
Now, we can subtract the whole rectangle area minus the non-shaded region to find the shaded region:
50 - 14 = 36
please please help last text then finals l give brainliest

Answers
1. The x - intercepts of the parabola are
x = 2.5 s and x = 7.5 s2. The meaning of the x-intercepts are the plane takes of at x = 2.5 s and lands at x = 7.5 s
3. The vertex of the parabola is at (5, 80).
What is a parabola?A parabola is a curved shape
1. Given the parabola above, to find the x - intercepts, we proceed as follows.
The x-intercepts are the points at which the graph cuts the x-axis.
They are
x = 2.5 s and x = 7.5 s2. The meaning of the x-intercepts in this problem are the points where the plane takes off and lands on the ground.
The plane takes of at x = 2.5 s and lands at x = 7.5 s
3. The vertex is the maximum point on the graph.
So, we see that the vertex is at x = 5 s and y = 80 ft
So, the vertex is at (5, 80).
Learn more about parabola here:
https://brainly.com/question/28094027
#SPJ1
Given that f(x) = 4x√3x + 3 and g(x) = 2√x+1, find (f/g)(x)

Answers
Answer:
\(2x\sqrt{3}.\)
Step-by-step explanation:
\(\frac{f}{g}(x)=\frac{4x\sqrt{3x+3}}{2\sqrt{x+1}}=\frac{2*2*x*\sqrt{3}*\sqrt{x+1}}{2*\sqrt{x+1}}=2x\sqrt{3}.\)
HEEELPPPPPPPP Rearrange the formula v = 2gh for h. A) h = v 2g B) h = 2v g C) h = v2 g D) h = v2 2g

Answers
Rearranging the equation, making h the subject of the formula, h = v² / 2g
How to rearrange formula?we rearrange equations and formulas by using inverse operations to make one variable the subject of the formula.
In order to change the subject of, or rearrange, a formula items in the formula need to be arranged so a different variable is the subject.
In our case the the formula needs to be rearrange to make h the subject of the formula.
Therefore,
v = √2gh
square both sides of the equation
v² = (√2gh)²
v² = 2gh
divide both sides by 2g
v² / 2g = 2gh / 2g
h = v² / 2g
Therefore,
h = v² / 2g
learn more on rearranging formula here: https://brainly.com/question/11067695
#SPJ1
Suppose a baker claims that the average bread height is more than 15cm. Several of this customers do not believe him. To persuade his customers that he is right, the baker decides to do a hypothesis test. He bakes 10 loaves of bread. The mean height of the sample loaves is 17 cm with a sample standard deviation of 1.9 cm. The heights of all bread loaves are assumed to be normally distributed. The baker is now interested in obtaining a 95% confidence interval for the true mean height of his loaves. What is the lower bound to this confidence interval? 2 cm (round to 2 decimal places) What is the upper bound to this confidence interval? cm (round to 2 decimal places) For the following situations, use RStudio to find the appropriate t-critical values that would be needed to construct a confidence interval. Round all critical values to the second decimal place. 1. n = 15, confidence level is 95%, x= 35 and s = 2.7, t-critical value- 2, n = 37, confidence level is 99%, x= 82 and s = 5.9 t-critical value- 2 3, n 1009, confidence level is 90%, x 0.9 and s-0.04 t- critical value = 2 2
Answers
The correct answer is Confidence interval lower bound: 32.52 cm,Confidence interval upper bound: 37.48 cm
To calculate the confidence interval for the true mean height of the loaves, we can use the t-distribution. Given that the sample size is small (n = 10) and the population standard deviation is unknown, the t-distribution is appropriate for constructing the confidence interval.
The formula for a confidence interval for the population mean (μ) is:
Confidence Interval = sample mean ± (t-critical value) * (sample standard deviation / sqrt(sample size))
For the first situation:
n = 15
Confidence level is 95% (which corresponds to an alpha level of 0.05)
x = 35 (sample mean)
s = 2.7 (sample standard deviation)
Using RStudio or a t-table, we can find the t-critical value. The degrees of freedom for this scenario is (n - 1) = (15 - 1) = 14.
The t-critical value at a 95% confidence level with 14 degrees of freedom is approximately 2.145.
Plugging the values into the formula:
Confidence Interval = 35 ± (2.145) * (2.7 / sqrt(15))
Calculating the confidence interval:
Lower Bound = 35 - (2.145) * (2.7 / sqrt(15)) ≈ 32.52 (rounded to 2 decimal places)
Upper Bound = 35 + (2.145) * (2.7 / sqrt(15)) ≈ 37.48 (rounded to 2 decimal places)
Therefore, the lower bound of the confidence interval is approximately 32.52 cm, and the upper bound is approximately 37.48 cm.
For the second situation:
n = 37
Confidence level is 99% (which corresponds to an alpha level of 0.01)
x = 82 (sample mean)
s = 5.9 (sample standard deviation)
The degrees of freedom for this scenario is (n - 1) = (37 - 1) = 36.
The t-critical value at a 99% confidence level with 36 degrees of freedom is approximately 2.711.
Plugging the values into the formula:
Confidence Interval = 82 ± (2.711) * (5.9 / sqrt(37))
Calculating the confidence interval:
Lower Bound = 82 - (2.711) * (5.9 / sqrt(37)) ≈ 78.20 (rounded to 2 decimal places)
Upper Bound = 82 + (2.711) * (5.9 / sqrt(37)) ≈ 85.80 (rounded to 2 decimal places)
Therefore, the lower bound of the confidence interval is approximately 78.20 cm, and the upper bound is approximately 85.80 cm.
For the third situation:
n = 1009
Confidence level is 90% (which corresponds to an alpha level of 0.10)
x = 0.9 (sample mean)
s = 0.04 (sample standard deviation)
The degrees of freedom for this scenario is (n - 1) = (1009 - 1) = 1008.
The t-critical value at a 90% confidence level with 1008 degrees of freedom is approximately 1.645.
Plugging the values into the formula:
Confidence Interval = 0.9 ± (1.645) * (0.04 / sqrt(1009))
Learn more about Confidence interval here:
https://brainly.com/question/15712887
#SPJ8