Using the t-table, please find the t-value for 90% confidence and nu space equals space 9?
Answers
The t-value for 90% confidence and nu=9 is 1.833.
To find the t-value using the t-table, we need to know the degrees of freedom (nu) and the desired confidence level. In this case, nu=9 and the confidence level is 90%.
Using a two-tailed t-table, we find the critical value of t for a 90% confidence interval and 9 degrees of freedom to be 1.833. This means that there is a 90% probability that the true population mean falls within 1.833 standard errors of the sample mean.
This value is important when constructing confidence intervals or conducting hypothesis tests with small sample sizes. A t-value is used to assess whether the difference between sample means is significant or due to chance.
A larger t-value indicates a larger difference between the sample means and a higher likelihood of statistical significance.
For more questions like Sample mean click the link below:
https://brainly.com/question/31101410
#SPJ11
Related Questions
If the sum of squares of the roots of the equation x² - 3ax + a² = 0 is equal to 4, find the value of a.
Answers
The value of a is 2/√7.
The given quadratic equation is x² ₋ 3ax ₊ a² = 0
sum of the roots of the equation = 4
here, A = 1
B = 3a
C = a²
Let α and β be the roots of the equation.
α ₊ β = ₋B/A
= ₋3a/1
= ₋3a
⇒ α×β = C/A
= a²/1
= a²
⇒α² ₊ β² = (α ₊ β )² ₋ 2αβ
= (₋3a)² ₋ 2(a²)
= 9a² ₋ 2a²
therefore, 7a² = 4
a² = 4/7
a = √4/7
a = 2/√7
Hence we found the value of a as 2/√7.
learn more about Quadratic equations here:
brainly.com/question/1214333
#SPJ9
Simultaneous equations.
3x+2y=11
x-y=2
I've been stuck on this wuestion for so long please help me.
Answers

Answer:
i think it is x=6/25 and y= 16/25
Step-by-step explanation:
Find the area of the surface obtained by rotating the curve y=1+5x2 from x=0 to x=2 about the y -axis. computed using the method of disks or washers via an integral
Answers
The surface area obtained by rotating about the y -axis is 168.159.
What is Integration?In mathematics, integration is a technique for combining or adding the parts to arrive at the total. It is a form of differentiation in reverse where we break down functions into their component elements. This technique is employed to determine the summation on a sizable scale.
We have the function y=1+5x² from x=0 to x=2 about the y -axis.
So, the Surface are is
S = 2π ∫ R(x) √ (1+ f'(x)²}
Then, f'(x) = 10x
Then, S = 2π ∫ R(x) √ (1+ f'(x)²}
= 2π ∫ (1+5x²) √ (1+100x²)
= 1/150 (401 (√401-1)) π
= 168.159
Learn more about Integration here:
https://brainly.com/question/18125359
#SPJ9
Elyse is building a square raised-bed garden with 4-foot sides. She measured the diagonal to be 4 to the square root of 2 feet. Is her garden square?
Answers
Elyse's garden is not a square because the length of the diagonal is not identical to the length of the sides.
what is square ?The geometric form known as a square has four equal-length sides and four right angles (90-degree angles). Each corner of a square connects to the other corner perpendicularly, and the diagonals (lines dividing the corners) are equally long. You can calculate a square's area by multiplying one of its edges by itself. The method for calculating a square's area is:
given
The square of the hypotenuse, or longest side, in a right triangle, is equivalent to the sum of the squares of the other two sides. Since the square's edges are all equal in this instance, the Pythagorean theorem is expressed as:
\(a^2 + a^2 = d^2\)
We can construct the equation if Elyse determined the diagonal to be 4 times the square root of 2 feet.
a sqrt = 4sqrt(2) (2)
When we simplify this solution, we obtain:
where an is the square's longest edge and d is the diagonal's length.
When we simplify this solution, we obtain:
\(2a^2 = d^2\)
a = 4 feet
Since the length of each diagonal can be determined using the Pythagorean theorem and Elyse's garden has sides measuring 4 feet, we can determine if her garden is square by computing the diagonal using the formula we created earlier:
5.656854249 feet is = to d = a sqrt(2)/4sqrt(2).
Elyse's garden is not a square because the length of the diagonal is not identical to the length of the sides.
To know more about square visit:
https://brainly.com/question/14198272
#SPJ1
a.) determine "a" in the given functions, so that "f" is continuous
b.) is "f" derivable overall with respect to the calculated "a" value?
f(x)= e-a, x<0 In(x+1), x ≥ 0
Answers
The value of "a" that makes the function "f" continuous can be determined by equating the two expressions for "f" at the point where x changes from negative to non-negative. In this case, that point is x = 0.
For "f" to be continuous at x = 0, we need to ensure that the left-hand limit and the right-hand limit of "f" are equal at x = 0.
Taking the left-hand limit as x approaches 0, we have lim(x→0-) \(e^(-a)\) = \(e^(-a)\).
Taking the right-hand limit as x approaches 0, we have lim(x→0+) ln(x+1) = ln(1) = 0.
Setting these two limits equal to each other, we get e^(-a) = 0.
Since\(e^(-a)\) is never equal to 0 for any real value of "a", there is no value of "a" that makes "f" continuous at x = 0. Therefore, "f" is not continuous overall for any value of "a".
Regarding the differentiability of "f", we can see that the second expression ln(x+1) is differentiable for x ≥ 0. However, the first expression \(e^(-a)\) is a constant function, and all constant functions are differentiable. Therefore, "f" is differentiable overall regardless of the value of "a".
Learn more about expression here:
https://brainly.com/question/15994491
#SPJ11
can sombody help me fast ? !

Answers
Answer:
i think D
Step-by-step explanation:
Which of the following is not an item in the income statement? SELECT ONLY ONE a. Discount allowed b. Furniture & Fixture c. Furniture & Fixture d. Discount received
Answers
The item that is not an item in the income statement is b. Furniture & Fixture as it is considered a fixed asset and is reported on the balance sheet instead.
The income statement, also known as the profit and loss statement, provides a summary of a company's revenues, expenses, gains, and losses over a specific period. It helps to assess the financial performance of a business. The income statement typically includes various items such as revenues, cost of goods sold, operating expenses, interest income or expense, and other gains or losses.
a. Discount allowed is a revenue item that represents the discounts given to customers as an incentive for early payment or other reasons. It is usually reported as a deduction from sales revenue.
c. Furniture & Fixture is not typically included in the income statement. Instead, it is considered a non-operating or non-recurring item and is generally classified as a fixed asset on the balance sheet. Fixed assets represent long-term investments made by a company for its operations.
d. Discount received is also not an item in the income statement. It represents the discounts received by a company from its suppliers for early payment or other reasons. Similar to discount allowed, it is usually reported as a deduction from the respective expense account.
In summary, b. Furniture & Fixture is the item that is not included in the income statement. It is considered a fixed asset and is reported on the balance sheet instead.
To know more about fixed assets, refer here:
https://brainly.com/question/14392032#
#SPJ11
Somebody help please I don’t understand

Answers
The constant of proportionality for respective problems is 2/7, 15, 2.75, 13, 4/3.
A) In the first block,
Using points we can find the equation of line ,
Using the formula (y - y₀) = m (x - x₀)
where m is the slope of the equation
The equation of line becomes 2x = 7y
⇒ y = 2/7x
⇒ 2/7 is the constant of proportionality
B) From the graph given,
Again Using the formula (y - y₀) = m (x - x₀)
If we consider two points,
(2,30) and (4,60)
The equation of line becomes
15x = y
Here, the constant of proportionality is 15.
C) It is given the equation is y = 2.75x
The constant of proportionality here is 2.75
D) It is given that,
The price of 5 games is $65.00
The price of 1 game will be 65 / 5
= $13.00
The equation becomes
y = 13x
So, the constant of proportionality becomes 13.
E) Let us consider 2 points (3,12) and (6,24)
The equation of line using the formula (y - y₀) = m (x - x₀) becomes 4x = 3y
⇒ y = 4/3 x
The constant of proportionality becomes 4/3.
To learn more about Constant of proportionality from given link
https://brainly.com/question/28413384
#SPJ1
if a coin is flipped 10 times what is the probability of approximately 5 heads, that is, exactly 4 or 5 or 6 heads?
Answers
The probability of getting approximately 5 heads (that is, exactly 4 or 5 or 6 heads) in 10 coin flips is 0.656 or about 65.6%.
The probability of approximately 5 heads in 10 coin flips can be calculated using the binomial distribution formula. This formula states that the probability of getting exactly k successes (in this case, heads) in n independent trials (coin flips) with a probability p of success on each trial (0.5 for a fair coin) is:
P(k successes) = (n choose k) * p^k * (1-p)^(n-k)
Where "n choose k" is the binomial coefficient, which represents the number of ways to choose k items from a set of n items (in this case, the number of ways to get k heads in n coin flips).
For this problem, we want to find the probability of getting either exactly 4, 5, or 6 heads in 10 coin flips. So we need to calculate the probability of each of these outcomes separately and then add them together:
P(4 heads) = (10 choose 4) * 0.5^4 * 0.5^6 = 0.205
P(5 heads) = (10 choose 5) * 0.5^5 * 0.5^5 = 0.246
P(6 heads) = (10 choose 6) * 0.5^6 * 0.5^4 = 0.205
The total probability of approximately 5 heads is the sum of these probabilities:
P(4 or 5 or 6 heads) = P(4 heads) + P(5 heads) + P(6 heads) = 0.656
Learn more about binomial distribution here:
brainly.com/question/31197941
#SPJ11
Starlin's goal is to spend less than $415 on a trip. So far, he has spent $25 on gas for his car. He will spend $100 each day on other expenses.
Let d represent the number of days for Starlin's trip.
Drag and drop the answer into the box to correctly complete the statement.
response - correct
Starlin's trip must last fewer than ___ days.
4
Answers
Answer: less than 4 days
Step-by-step explanation:
415 - 25 = 390
if ur spending 100 each day then
day 1 = 290
day 2 = 190
day 3 = 90
he needs to spend less than 4 days
I got 5x+8 but I don’t know what to do after this, please help!

Answers
who out there plays imvu
Answers
Answer:
what?
Step-by-step explanation:
Answer:
I play imvu and troll
Step-by-step explanation:
PPL BE THICC
Trent and his family are heading to Perfect Putt Mini-Golf. They plan to purchase the group
package. With the package, the cost per person is $3 less than the normal cost for an
individual. There are 6 people in Trent's family. His mom called ahead and found that the total
cost for the family will be $30.
Which equation can you use to find the normal cost, x, for an individual?
A. 3(x-6)= 30
B. 6x-3 = 30
C. 6(x-3) = 30
D. 3x-6=30
Answers
Answer:
C
Step-by-step explanation:
Step by step explanation:
Find x, if 1/3 of x is equal to 21
Answers
Answer:
63
Step-by-step explanation:
21 x 3 = 63
i think this is right l:
The solution for the given algebraic equation is 63
How do I calculate x in the given equation ?Bring the variable to one side of the equation and all the remaining values to the other side by performing arithmetic operations on both sides of the equation. To determine the answer, simplify the values.Find the value of x that would make the equation you're looking at true. Consider the following equation: x + 1 Equals 3. If you were asked to solve it, you would need to discover some value for x that adds up to three.In algebra, the letter "x" is frequently used to represent an unknown value. It is referred to as a "variable" or "unknown" at times.
\(\frac{1}{3} x = 21\)
x = 3*21 =63
To learn more about algebraic equation refer,
https://brainly.com/question/2164351
#SPJ2
what is greater: 19/5, 27/5, 10/3, 14/5
Answers
Answer:
I think the greater fraction is 27/5
Answer:
27/5Step-by-step explanation:
what is greater: 19/5, 27/5, 10/3, 14/5
fractions are divisions, we divide to see the greater
19/5= 3.8
27/5= 5.4
10/3= 3.33
14/5= 2.8
Help 9th grade math please please please

Answers
Answer:
A.) This system has no solutions.
Step-by-step explanation:
y = 1/2x + 4
-1/2x + y = -5
-1/2x + (1/2x + 4) = -5
4 = -5
The system has no solutions, if we graph it, we get that it has the same slope with two different y-intercepts, these two are parallel. These two points will never meet at a point.

Answer:
use the relationship between coefficients of a pair of linear equations for no solutions i.e. a1/a2 equal to b1/b2 not equal to c1/c2 .
Here, a is coefficient of x and b is coefficient of y and c is constant term in both equation but make sure that you put the values of a1,a2,b1,b2,c1 and c2 after converting both equation in the form ax+by+c=0 with proper sign and here y=1/2(x) +4 is equation 1 and other is equation 2
5.93 A roulette payoff revisited. Refer to the previous exercise. In part (d), the central limit theorem was used to approximate the probability that Sam ends the year ahead. The estimate was about 0.10 too large. Let’s see if we can get closer using the Normal approximation to the binomial with the continuity correction. (a) If Sam plans to bet on 520 roulette spins, he needs to win at least $520 to break even. If each win gives him $35, what is the minimum number of wins m he must have? (b) Given p = 1/38 = 0.026, what are the mean and standard deviation of X, the number of wins in 520 546 roulette spins? (c) Use the information in the previous two parts to compute P(X ≥ m) with the continuity correction. Does your answer get closer to the exact probability 0.396?
Answers
a) The minimum number of wins he needs is 15. b) The standard deviation of X is σ = sqrt(Var(X)) ≈ 3.641. c) Standard normal table ≈ 0.411.
In part (a), we can use the formula for a binomial distribution to find the minimum number of wins Sam needs to break even. Let X be the number of wins in 520 spins, then X ~ Bin(520, 1/38). To break even, Sam needs to win at least $520, which means he needs at least m wins where 35m ≥ 520, or m ≥ 14.86. Since m must be an integer, the minimum number of wins he needs is 15.
In part (b), we can use the mean and variance of a binomial distribution to find the mean and standard deviation of X. The mean of X is E(X) = np = 520*(1/38) ≈ 13.684, and the variance of X is Var(X) = np(1-p) = 520*(1/38)*(37/38) ≈ 13.255. Therefore, the standard deviation of X is σ = sqrt(Var(X)) ≈ 3.641.
In part (c), we can use the Normal approximation to the binomial with the continuity correction to find P(X ≥ 15). Using the continuity correction, we can convert the discrete probability P(X ≥ 15) to a continuous probability P(X > 14.5). Standardizing X, we get Z = (14.5 - 13.684) / 3.641 ≈ 0.224. Using a standard normal table, we can find that P(Z > 0.224) ≈ 0.411. Therefore, P(X > 14.5) ≈ 0.411.
This answer is closer to the exact probability of 0.396 than the previous estimate of 0.10 too large, but it still overestimates the probability slightly. This could be due to the fact that the Normal approximation to the binomial assumes a continuous distribution, while the binomial distribution is discrete. Nonetheless, the Normal approximation with continuity correction is a useful tool for approximating probabilities in situations where the sample size is large.
To learn more about standard deviation click here
brainly.com/question/23907081
#SPJ11
Michael has a bag of marbles. The frequency of selecting each color is recorded in the table below.
Outcome Frequency
Green 4
Black 6
Orange 5
Based on the given frequency, determine the experimental probability of selecting an orange marble.
0.27
0.33
0.40
0.67
Answers
The probability of selecting an orange marble is 0.33.
Option B is the correct answer.
What is probability?It is the chance of an event to occur from a total number of outcomes.
The formula for probability is given as:
Probability = Number of required events / Total number of outcomes.
We have,
The number of times each marble is selected.
Green = 4
Black = 6
Orange = 5
Total number of times all marbles are selected.
= 4 + 6 + 5
= 15
Now,
The probability of selecting an orange marble.
= 5/15
= 1/3
= 0.33
Thus,
The probability of selecting an orange marble is 0.33.
Learn more about probability here:
https://brainly.com/question/14099682
#SPJ1
find the linear approximation l(x) to y = f(x) near x = a for the function. f(x) = 1 x , a = 4
Answers
The linear approximation, denoted as l(x), to the function f(x) = 1/x near x = 4 is given by the equation l(x) = f(a) + f'(a)(x - a). In this case, a = 4, so we need to find f(a), f'(a), and substitute them into the equation to obtain the linear approximation.
First, we find f(a) by substituting a into the function f(x). Thus, f(4) = 1/4.
Next, we need to determine f'(a), which represents the derivative of f(x) with respect to x, evaluated at x = a. The derivative of f(x) = 1/x is found by applying the power rule of differentiation. The derivative f'(x) = -1/x^2. Substituting a = 4, we get f'(4) = -1/(4^2) = -1/16.
Now, we can substitute f(a) and f'(a) into the linear approximation equation. Therefore, l(x) = 1/4 - (1/16)(x - 4).
In summary, the linear approximation l(x) to the function f(x) = 1/x near x = 4 is given by l(x) = 1/4 - (1/16)(x - 4). This approximation provides an estimate of the function's behavior in the vicinity of x = 4 using a linear equation.
To derive the linear approximation, we first determine f(a) by substituting a = 4 into the original function f(x) = 1/x. This yields f(4) = 1/4. Then, we find f'(x), the derivative of f(x) with respect to x, using the power rule of differentiation. The derivative f'(x) = -1/x^2. Evaluating this at x = 4 gives us f'(4) = -1/(4^2) = -1/16. Finally, we substitute f(a) and f'(a) into the linear approximation equation l(x) = f(a) + f'(a)(x - a) to obtain the final expression l(x) = 1/4 - (1/16)(x - 4). This equation provides an approximate representation of the original function near x = 4, allowing us to estimate its behavior using a simpler linear function.
Learn more about linear approximation here: brainly.com/question/30403460
#SPJ11
if the equation y=4x-5 is changed to y=1/4x-5 how is the graph affected
1) the line is shifted up
2) the line is closer to verticale
3) the line is closer to horizontal
4) the line is decreasing from left to right
5) the line is decreasing from right to left
Answers
3) the line is closer to horizontal
it has flipped from 4/1 to 1/4
4/1 means up 4 and over one(just 4x)
1/4 means up one and over four(1/4x)
The line is still going the same direction, it has just
moved closer to being a horizontal line
Find the slope of the line.

Answers
Answer:
4/1 is the answer
Step-by-step explanation:
hope this helps
5w+4w=18 simplify
how do you do this??
Answers
Answer:
Solved: w = 2
Step-by-step explanation:
Combine like terms
5w+4w = 9w
Isolate or make w alone
9w= 18 so divide both sides by 9 to make w alone
9w ÷ 9 = w
18 ÷ 9 = 2
w = 2
Answer:
you just add 5w and 4w and taht is 9w
\(9x = 18 \\ w = 18 \div 9 \\ w = 2\)
Please answer question

Answers
Answer:
346.4 cm^2
Step-by-step explanation:
area = base * height/2
We can use UW as the base.
U + V + W = 180
24 + V + 36 = 180
V = 120
\( \dfrac{\sin W}{UV} = \dfrac{\sin V}{UW} \)
\( \dfrac{\sin 36^\circ}{34} = \dfrac{\sin 120^\circ}{UW} \)
\( UW = \dfrac{34\sin 120^\circ}{\sin 36^\circ} \)
\( UW = 50.1 \)
Now drop a perpendicular from V to UW to be the height, h.
\(\sin 24^\circ = \dfrac{h}{UV}\)
\( \sin 24^\circ = \dfrac{h}{34} \)
\( h = 34 \sin 24^\circ \)
\( h = 13.8 \)
area = base * height/2
area = UW * h/2
area = 50.1 cm * 13.8 cm/2
area = 346.4 cm^2
A state trooper used a radar gun to measure the speed (in miles per hour) of all the cars that drove past her stretch of highway in a twenty minute period. She separated the results by whether the cars were traveling northbound or southbound. The histograms show the speed of each car that she recorded.
Which statement is an appropriate inference based on the median of each data set?
Question 4 options:
1.)The northbound cars were generally faster because the median for the northbound cars is less than the median for the southbound cars.
2.)The northbound cars were generally faster because the median for the northbound cars is greater than the median for the southbound cars.
3.)The southbound cars were generally faster because the median for the northbound cars is less than the median for the southbound cars.
4.)The southbound cars were generally faster because the median for the northbound cars is greater than the median for the southbound cars.
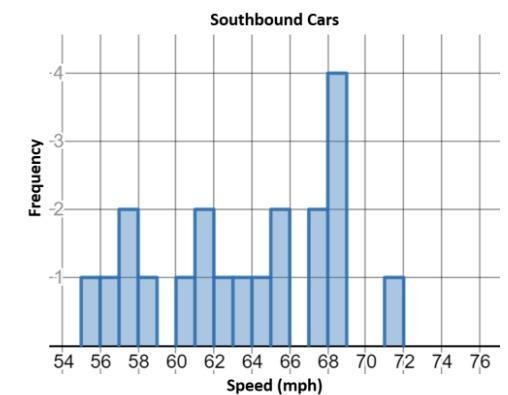

Answers
Answer:
2.
Step-by-step explanation:
There are more boxes towards the highest numbers which means that the medians for northbound cars are generally high while the medians for southbound cars are located more on the smaller numbers representing the speed.
2.5. For his homework Thulani defined a factor as: "Factors of a number are formed when the number is multiplied by 1; 2; 3; 4". You realise that Thulani has a misconception when it comes to factors and multiples. (5) N 2.5.1 Identify and write down the misconception that Thulani has (2)
Answers
Answer:
we are interested to give your answer so I am with you forever
Calculate the circumference and area of this circle.

Answers
Answer:
circumference 69.08 area 379.94
Step-by-step explanation:
Scenario 1: Cameron works at a local grocery store after school. He is paid $8 for each hour he works.
Scenario 2: At a local bakery, one box of donuts costs $5. Two boxes of donuts cost $10.
Consider the two scenarios given above. Can you write an equation to represent each situation? What would the graphs of these equations look like? Can you think of a situation that would result in a similar equation?
Answers
Answer:
1: Linear
2: Linear
Step-by-step explanation:
Scenario 1:
Equation: y=8x (where x represents # of hours worked)
The graph would be linear.
Scenario2:
Equation: y=5x (where x is the # of boxes of donuts purchased)
The graph would be linear. ( I assumed that each box is $5 since 5/1=10/2 )
A similar situation could be: In an art shop, crayons are sold. It costs $7 for 1 box of crayons.
- The graph would be linear, and it would be constant as long as the price for each box of crayons is not changed. Equation is: y=7x
I'm not sure if this is exactly what the last question asked, pretty sure this would be an okay example.
In 1895, the first a sporting event was held. The winners prize money was 150. In 2007, the winners check was 1,163,000. (Do not round your intermediate calculations.)
What was the percentage increase per year in the winners check over this period?
If the winners prize increases at the same rate, what will it be in 2040?
Answers
The estimated winners' prize in 2040, assuming the same rate of increase per year, is approximately $54,680,580,063,400.
The initial value is $150, and the final value is $1,163,000. The number of years between 1895 and 2007 is 2007 - 1895 = 112 years.
Using the formula for percentage increase:
Percentage Increase = [(Final Value - Initial Value) / Initial Value] * 100
= [(1,163,000 - 150) / 150] * 100
= (1,162,850 / 150) * 100
= 775,233.33%
Therefore, the winners' check increased by approximately 775,233.33% over the period from 1895 to 2007.
To estimate the winners' prize in 2040, we assume the same rate of increase per year. We can use the formula:
Future Value = Initial Value * (1 + Percentage Increase)^Number of Years
Since the initial value is $1,163,000, the percentage increase per year is 775,233.33%, and the number of years is 2040 - 2007 = 33 years, we can calculate the future value:
Calculating this expression:
Future Value = 1,163,000 * (1 + 775,233.33%)^33
Using a calculator or computer software, we can evaluate this expression to find the future value. Here's the result:
Future Value ≈ $1,163,000 * (1 + 77.523333)^33 ≈ $1,163,000 * 47,051,979.42 ≈ $54,680,580,063,400
Therefore, based on the assumed rate of increase per year, the estimated winners' prize in 2040 would be approximately $54,680,580,063,400.
Learn more about Expressions click here :brainly.com/question/24734894
#SPJ11
Find the slope between (2, 4) and (0, -2). Then, write the equation of the line in slope-intercept form.
Answers
Answer:
3
Step-by-step explanation:
m = -6 / -2 = -3 / -1 = 3
This was it!!!!!!!!!!!!!!! The model

Answers
Answer:
a
Step-by-step explanation:
The block is divided into 7 pieces.
We need 4 of one color, 2 of another color, and one of a third color
4/7 + 2/7 + 1/7