Using composition of functions, determine if the two functions are inverses
of each other.
F(x)=√x-6
G(x) = (x+6)²
OA. Yes, but only within the domain x ≥ 0.
OB. No, because the composition does not result in an answer of x.
OC. Yes, because F(x) is equal to - G(x).
OD. No, because the functions contain different operations.
Answers
Answer:
A. Yes, but only within the domain x ≥ 0
Step-by-s+tep explanation:
What you need to know to solve the question:
1. To find an inverse function (f⁻¹(x)) of f(x), rearrange the equation in terms of f(x), in other words, it should be in the form of x = ...
2. Rules of rearranging equations
3. The domain of √x is: x ≥ 0, since you cannot find the square root of a negative number (i.e. < 0)
Find the inverse function of F(x):
According to principles 1 and 2:
F(x) = √x - 6
F(x) + 6 = √x
(F(x) + 6)² = x
x = (F(x) + 6)²
So, the inverse function is:
F⁻¹(x) = (x + 6)²
And since:
G(x) = (x + 6)²
G(x) = F⁻¹(x)
Therefore, the answer is, also in light of principle 3:
A. Yes, but only within the domain x ≥ 0
Related Questions
HELP will make you branlist pls pls HELP will make you branlist pls pls

Answers
Slope = rate of change
Find two random points
(0,3) and (2,0)
Now use (y2-y1)/(x2-x1) to find slope
(0-3)/(2-0) = -3/2 is the slope
Now find y intercept
Y intercept is when x = 0, (0,y)
Therefore y intercept is (0,3)
Slope intercept form: y = mx + b
m = slope, b = y intercept
Answer: y = -3/2x + 3
Based on the pattern, what are the next two terms of the sequence?

Answers
Answer:
33 , 39
Step-by-step explanation:
given
9 , 15 , 21 , 27
there is a common difference between consecutive terms, that is
15 - 9 = 21 - 15 = 27 - 21 = 6
to obtain terms in the sequence add 6 to the preceding term
27 + 6 = 33
33 + 6 = 39
the next two terms are 33 and 39
15-9=6
21-15=6
27-21=6
That means we are adding 6 at every step. Therefore the next two elements must be
27+6=33 and 33+6=39
Not homework BUT
Let’s say you had 597 wins and 1081 losses
You were to add 6 wins and 4 losses everyday
How long would it take for you to break even on your wins and losses considering it stays consistent
Answers
Answer:
242 days
Step-by-step explanation:
1081-597=484
it is increasing by 2wins every day so 484/2=242 days
The Marching Band ordered 14 pizzas for a party. Each pizza had 8 slices. Dan ate 9 of the slices. How many slices were left for the rest of the band?
Answers
Answer:
103
Step-by-step explanation:
14 x 8 =112 - 9 =103
Answer:
The Correct Answer is 103 slices.
Step-by-step explanation:
14 x 8 = 112
112 - 9 = 103
i dont know how he could eat 9 slices at once, but so be it :shrug: lol
Hope This Helps!
A shipping container will be used to transport several 50-kilogram crates across the country by rail. The greatest weight that can be loaded into the container is 24000 kilograms. Other shipments weighing 11600 kilograms have already been loaded into the container. Write and solve an inequality which can be used to determine xx, the number of 50-kilogram crates that can be loaded into the shipping container.
Answers
The greatest weight that can be loaded into the container is 24000 kilograms.
Let y be the weight of the container
\(y\le24000\)Already loaded 11600 Kg in the container.
\(y\le24000-11600\)\(y\le12400\)It can be loaded with several 50kg crates.
\(50x\le y\)The equation to find the x number of 50 kg crates is
\(50x\le12400\)\(x\le\frac{12400}{50}\)\(x\le248\)Hence the number of 50-
Polygon ABCD slides 4 units left and 3 units up on the coordinate plane. If the original measure of angle A was 75 degrees, what is the measure of angle A′
Answers
it would still be 75, because translations preserve angle measures
Lisa paid $43.95 for 16.1 gallons of gasoline. What was the cost per gallon rounded to the nearest hundredth?
Answers
Answer$ 2.73 per gallon
Step-by-step explanation:
A coin bank has 17 coins that contains only dimes and quarters. The coins are worth $3.35. How many of each coin are in the bank?
Answers
Answer:7 quarters and 6 dimes
Step-by-step explanation:
Select the correct answer.
What is the relationship between the two shapes?
LOOK AT THE IMAGE PLEASE

Answers
The answer is the A because they are similar and congruent
Answer:
A
Step-by-step explanation:
Please help what is the slope of the line?
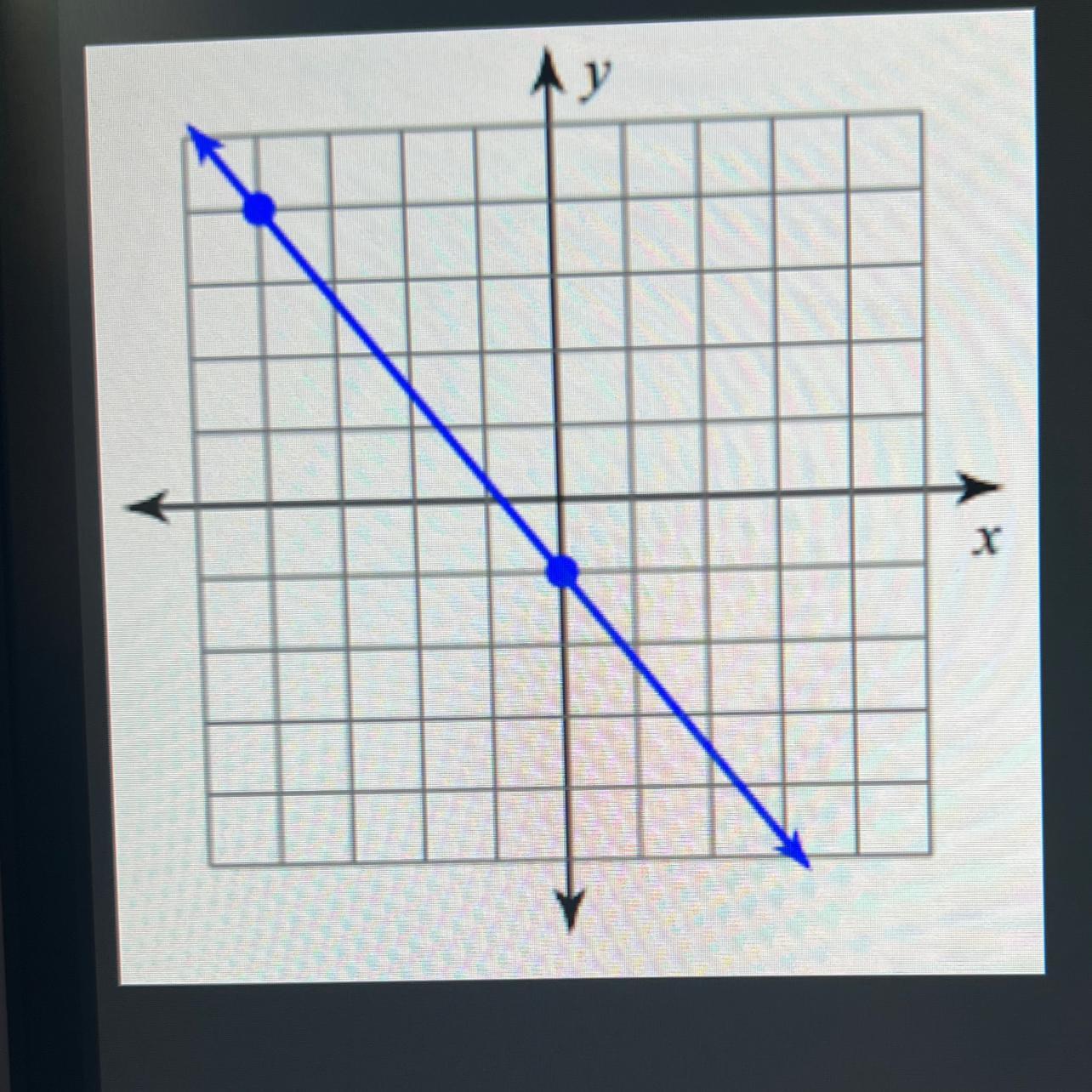
Answers
Answer:
-5/4
Step-by-step explanation:
Let \((x_1,y_1)=(-4,4)\) and \((x_2,y_2)=(0,-1)\). The slope of the line would be:
\(\displaystyle \frac{y_2-y_1}{x_2-x_1}=\frac{-1-4}{0-(-4)}=\frac{-5}{4}=-\frac{5}{4}\)
Answer: -5/4
Step-by-step explanation:
To find the slope between two points, you can use the formula:
Slope = (y2 - y1)/(x2 - x1)
Using the points (0, -1) and (-4, 4), we can substitute the coordinates into the formula:
slope = (4 - (-1))/(-4 - 0)
slope = (4 + 1)/(-4)
slope = 5/-4
Therefore, the slope between the two points is -5/4.
Find an equation of the osculating plane and an equation of the normal
plane of the curve x = sin 2t, y = t, z = cos 2t at the point (0, π, 1).
Answers
The equation of the normal plane is 4y = 4π, or equivalently, y = π.
What is osculating plane?The word osculate comes from the Latin osculatus, which is a past participle of the verb osculari, which means "to kiss." Thus, an osculating plane is one that "kisses" a submanifold.
To find the osculating plane and normal plane of the curve x = sin 2t, y = t, z = cos 2t at the point (0, π, 1), we need to follow these steps:
Find the first and second derivatives of the curve with respect to t.Evaluate the derivatives at t = π to get the velocity, acceleration, and curvature vectors at the point (0, π, 1).Use the velocity and acceleration vectors to find the normal vector of the osculating plane.Use the normal vector and the point (0, π, 1) to find the equation of the osculating plane.Use the curvature vector to find the normal vector of the normal plane.Use the normal vector and the point (0, π, 1) to find the equation of the normal plane.Step 1: Find the first and second derivatives of the curve with respect to t.
x' = 2cos2t
y' = 1
z' = -2sin2t
x'' = -4sin2t
y'' = 0
z'' = -4cos2t
Step 2: Evaluate the derivatives at t = π.
x'(π) = 2cos2π = 2
y'(π) = 1
z'(π) = -2sin2π = 0
x''(π) = -4sin2π = 0
y''(π) = 0
z''(π) = -4cos2π = -4
So the velocity vector at the point (0, π, 1) is v = ⟨2, 1, 0⟩, the acceleration vector is a = ⟨0, 0, -4⟩, and the curvature vector is κv = ⟨0, 4, 0⟩.
Step 3: Use the velocity and acceleration vectors to find the normal vector of the osculating plane.
The normal vector of the osculating plane is given by the cross product of the velocity and acceleration vectors:
n = v × a = ⟨2, 1, 0⟩ × ⟨0, 0, -4⟩ = ⟨4, 0, 0⟩
Step 4: Use the normal vector and the point (0, π, 1) to find the equation of the osculating plane.
The equation of the osculating plane is given by:
4(x - 0) + 0(y - π) + 0(z - 1) = 0
Simplifying, we get:
4x - 4 = 0
So the equation of the osculating plane is 4x = 4, or equivalently, x = 1.
Step 5: Use the curvature vector to find the normal vector of the normal plane.
The normal vector of the normal plane is given by the curvature vector:
n' = κv = ⟨0, 4, 0⟩
Step 6: Use the normal vector and the point (0, π, 1) to find the equation of the normal plane.
The equation of the normal plane is given by:
0(x - 0) + 4(y - π) + 0(z - 1) = 0
Simplifying, we get:
4y - 4π = 0
So, the equation of the normal plane is 4y = 4π, or equivalently, y = π.
Learn more about derivatives on:
https://brainly.com/question/23819325
#SPJ1
(01.02 MC)which value is equivalent to 8x4x2
Answers
Answer:
64
Step-by-step explanation:
Multiplication
8 * 4 = 32
32* 2 = 64
The graph of the absolute value parent function, f(x) = |x), is stretched
horizontally by a factor of 3 to create the graph of g(x). What function is g(x)?
OA. g(x)= x+3|
OB. g(x) = 31x1
C. g(x) = 13x1
OD. g(x)= |||

Answers
Answer:
OB. g(x) = 31x1
C. g(x) = 13x1
Step-by-step explanation:
The National Association of Home Builders provided data on the cost of the most popular home remodeling projects. Sample data on cost in thousands of dollars for two types of remodeling projects are as follows. KitchenMaster Bedroom 25.218.017.422.922.826.421.924.819.726.923.017.819.724.616.921.021.823.6a) Develop a point estimate of the difference between the population mean remodeling costs for the two types of projects.b) Develop a 90% confidence interval for the difference between the two population means.
Answers
Answer:
Kitchen
25.2
17.4
22.8
21.9
19.7
amp;Master Bedroom
amp;18
amp;22.9
amp;26.4
amp;24.8
amp;26.9
amp;Kitchen
amp;23
amp;19.7
amp;16.9
amp;21.8
amp;23.6
amp;Master Bedroom
amp;17.8
amp;24.6
amp;21
Step-by-step explanation:
Triangle ABC has coordinates A(-3, 4), B(3, 2), and C(1, -2). Find the area of triangle ABC.

Answers
Step 1: Write out the formula for finding the area of traingle given the three coordinates
\(\begin{gathered} \text{say:} \\ A(x_1,y_1);B(x_2,y_2);C(x_3,y_3) \\ \text{Area}=\frac{1}{2}(x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2) \end{gathered}\)Step 2: Write out the given parameters
\(\begin{gathered} A(-3,4);B(3,2);C(1,-2) \\ x_1=-3;y_1=4 \\ x_2=3;y_2=2 \\ x_3=1;y_3=-2 \end{gathered}\)Step 3: Substitute the parameters into the formula
\(\begin{gathered} \text{Area}=\frac{1}{2}(-3(2--2)+3(-2-4)+1(4-2)) \\ =\frac{1}{2}(-3(4)+3(-6)+1(2)) \\ =\frac{1}{2}(-12-18+2) \\ =\frac{1}{2}(-28) \\ \text{Area}=\lvert-14\rvert \\ A=14 \end{gathered}\)Hence, the area is 14square unit
At what rate per annum compound
interest will N4000 amount to N5353
in 5 years?
Answers
Answer: Just look it up on goo gle
Step-by-step explanation:
The rate per annum compound interest is approximately 11.5%.
To find the rate per annum compound interest, we can use the formula for compound interest:
\(A = P(1 + r/n)^{nt}\)
Where:
A = the final amount (N5353 in this case)
P = the principal amount (N4000 in this case)
r = the annual interest rate (what we want to find)
n = the number of times interest is compounded per year (assuming once per year)
t = the number of years (5 years in this case)
Now, we can plug in the values:
\(N5353 = N4000(1 + r/1)^{1*5}\)
Divide both sides by N4000:
\(1.33825 = (1 + r)^5\)
Now, isolate (1 + r) by taking the fifth root of both sides:
\(1 + r = (1.33825)^{1/3}\\1 + r \approx 1.115\)
Now, subtract 1 from both sides to find the interest rate (r):
r ≈ 1.115 - 1
r ≈ 0.115
Finally, convert the interest rate to a percentage:
r ≈ 0.115 * 100
r ≈ 11.5%
To know more about rate:
https://brainly.com/question/32398403
#SPJ2
5.3 MATHEMATICS HOLIDAY PACKAGE-TERM 2(2023) Instructions: Attempt ALL items 1. Your family has seven siblings; peter, John, Sarah, Joy, Ali, Mary and Ivan. There is an interval of 2 years between the ages of the children from Ivan to peter. Ivan is three years old. Task: Using an arrow diagram, explain the information about your family.
Answers
What is 4 3/5 of 45?
Answers
Answer: 207
Step-by-step explanation:
Let's start by converting 4 3/5 to an improper fraction. We do this by multiplying 4 * 5 and adding it to 3. This full equation is (4 * 5) + 3 = 23. We then have 23/5. We multiplying this by 45 to get our answer. This is done by multiplying 23 * 45 and then dividing that by 5. This full equation is (23 * 45) / 5 = 207. Therefore, our answer is 207.
The equation y-20000(0.95)* represents the purchasing power of $20,000, with an inflation rate of five percent. X represents the
number of years
Use the equation to predict the purchasing power in five years.
Round to the nearest dollar.
$15,476
$17,652
$18,523
$19,500
Answers
The purchasing power in five years will be $15,476.
To predict the purchasing power in five years, we can substitute the value of X as 5 into the equation y = 20000(0.95)^X.
Plugging in X = 5, we have:
\(y = 20000(0.95)^5\)
Calculating the expression, we find:
\(y ≈ 20000(0.774)\)
Simplifying further, we get:
\(y ≈ 15480\)
Rounding the result to the nearest dollar, the predicted purchasing power in five years would be approximately $15,480.
Therefore, the closest option to the predicted purchasing power in five years is $15,476.
So the correct answer is:
$15,476.
For more questions on purchasing
https://brainly.com/question/27975123
#SPJ8
Rounding to the nearest dollar, the predicted purchasing power in five years is approximately $15,480.
To predict the purchasing power in five years using the given equation, we substitute the value of x (representing the number of years) as 5 and calculate the result.
The equation provided is: y = 20000(0.95)^x
Substituting x = 5 into the equation, we have:
y = 20000(0.95)⁵
Now, let's calculate the result:
y ≈ 20000(0.95)⁵
≈ 20000(0.774)
y ≈ 20000(0.774)
≈ 15,480
This means that, according to the given equation, the purchasing power of $20,000, with an inflation rate of five percent, would be predicted to be approximately $15,480 after five years.
By changing the value of x (representing the number of years) to 5, we can use the preceding equation to forecast the buying power in five years.
The example equation is: y = 20000(0.95)^x
When x = 5 is substituted into the equation, we get y = 20000(0.95).⁵
Let's now compute the outcome:
y ≈ 20000(0.95)⁵ ≈ 20000(0.774)
y ≈ 20000(0.774) ≈ 15,480
This indicates that based on the equation, after five years, the purchasing power of $20,000 would be estimated to be around $15,480 with a five percent inflation rate.
For similar questions on purchasing power
https://brainly.com/question/3794707
#SPJ8
The College Board states that the average math SAT score is 514 with a standard deviation of 117. Colleen knows scores at her school are normally distributed and collects a random sample of 50 students in her graduating class. Give a 95% confidence interval for the population mean. Round to the nearest tenth.
Answers
In hypothesis testing, null hypothesis (H0) is a claim that the person conducting the research wants to test while an alternative hypothesis (H1) is a contradiction of the null hypothesis.
There are two types of tests in hypothesis testing is known.
One tailed test: In first tailed test, a claim that a parameter is greater than/ less than a value is being tested.
mean > value or mean < value.
Second tailed test: In a two tailed test, a claim that a value is equal to a value is tested,
mean = value.
Since we can see that Colleen is testing the claim that the average score of her class is the same as others against that it is different from others.
Hence, the null hypothesis is H0: mean = 514
and the alternative hypothesis is H1: mean ≠ 514
Learn more about type I and type II errors here:
https://brainly.com/question/26067196
#SPJ1
A class contains 5 girls and 7 boys. Two are selected for a class committee. What is the probability that a girl and boy are selected?
Answers
The probability of selecting a girl and a boy for the class committee can be calculated by considering the total number of outcomes and the number of favorable outcomes.
Identify the number of girls and boys in the class. In this case, there are 5 girls and 7 boys.
Determine the total number of students in the class. That is 5 + 7 = 12.
Determine the number of ways to select two students from the class.
Here we can use the combination formula, which is written as C(n, r), where n is the total number of items and r is the number of items to be chosen.
In our case, n = 12 (total number of students) and r = 2 (number of students to be selected).
C(12, 2) = 12! / (2!(12-2)!) = 66.
Determine the number of favorable outcomes.
In this case, we want to select one girl and one boy. We multiply the number of girls by the number of boys: 5 x 7 = 35.
To find the probability, we divide the number of favorable outcomes (35) by the total number of outcomes (66):
Probability = Number of favorable outcomes / Total number of outcomes = 35 / 66 = 5/6.
So, the probability of selecting a girl and a boy for the class committee is 5/6.
Read more about probability,
https://brainly.com/question/30390037
food concession owner in a mall sold 120 beef, vegetable and pork sliders in 7 days. 20% of the sliders sold were beef and 15% were vegetable. How many pork sliders were sold?
Answers
The number of pork sliders sold is given as follows:
24 pork sliders.
How to obtain the number of pork sliders sold?The number of pork sliders sold is obtained applying the proportions in the context of the problem.
The total number of pork sliders is given as follows:
120 pork sliders.
The percentage of pork sliders sold is given as follows:
20%. (proportion of 0.2).
Hence the amount sold is given as follows:
0.2 x 120 = 24 pork sliders.
More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1
The area of a circle is equal to 1 dm2. Find the radius of the circle.
Answers
Answer:
2000
Step-by-step explanation:
1 dm =1000
2dm =?
2dm x 1000
1dm
2000
Difference between the two sets
\( \\ \\ \)
Let A = {1, 2, 3, 4, 5, 6, 7} B = {1, 3, 5, 7, 9} C = {0, 2, 4, 6, 10} Find the difference of the given pair of sets.
1.) A - B
2.) B - A
3.) (A ∪ B) - C
Answers
Answer:
1) A - B = {2, 4, 6}
2) B - A = {9}
3) (A ∪ B) - C = {1, 3, 5, 7, 9}
Step-by-step explanation:
Set Notation
\(\begin{array}{|c|c|l|} \cline{1-3} \sf Symbol & \sf N\:\!ame & \sf Meaning \\\cline{1-3} \{ \: \} & \sf Set & \sf A\:collection\:of\:elements\\\cline{1-3} \cup & \sf Union & \sf A \cup B=elements\:in\:A\:or\:B\:(or\:both)}\\\cline{1-3} \cap & \sf Intersection & \sf A \cap B=elements\: in \:both\: A \:and \:B} \\\cline{1-3} \sf ' \:or\: ^c & \sf Complement & \sf A'=elements\: not\: in\: A \\\cline{1-3} \sf - & \sf Difference & \sf A-B=elements \:in \:A \:but\: not\: in \:B}\\\cline{1-3} \end{array}\)
Given sets:
A = {1, 2, 3, 4, 5, 6, 7}B = {1, 3, 5, 7, 9}C = {0, 2, 4, 6, 10}Question 1
\(\begin{aligned}\sf A-B & =\sf \{ 1, 2, 3, 4, 5, 6, 7 \} - \{1, 3, 5, 7, 9 \}\\& =\sf \{ 2, 4, 6 \}\end{aligned}\)
Question 2
\(\begin{aligned}\sf B-A & =\sf \{1, 3, 5, 7, 9 \} - \{ 1, 2, 3, 4, 5, 6, 7 \}\\& =\sf \{9 \}\end{aligned}\)
Question 3
\(\begin{aligned}\sf (A \cup B)-C & =\sf \left(\{ 1, 2, 3, 4, 5, 6, 7 \} \cup \{1, 3, 5, 7, 9 \} \right) - \{0, 2, 4, 6, 10 \}\\& =\sf \{ 1, 2, 3, 4, 5, 6, 7, 9 \} - \{0, 2, 4, 6, 10 \}\\& = \sf \{ 1, 3, 5, 7, 9 \}\end{aligned}\)
Learn more about set notation here:
https://brainly.com/question/28356437
https://brainly.com/question/28353607
Suppose that we want to generate the outcome of the flip of a fair coin, but that all we have at our disposal is a biased coin which lands on heads with some unknown probability p that need not be equal to1/2. Consider the following procedure for accomplishing our task:
1. Flip the coin.
2. Flip the coin again.
3. If both flips land on heads or both land on tails, return to step 1. 4. Let the result of the last flip be the result of the experiment.
(a) Show that the result is equally likely to be either heads or tails.
(b) Could we use a simpler procedure that continues to flip the coin until the last two flips are different and then lets the result be the outcome of the final flip?
Answers
Answer:
Step-by-step explanation:
Given that;
the following procedure for accomplishing our task are:
1. Flip the coin.
2. Flip the coin again.
From here will know that the coin is first flipped twice
3. If both flips land on heads or both land on tails, it implies that we return to step 1 to start again. this makes the flip to be insignificant since both flips land on heads or both land on tails
But if the outcomes of the two flip are different i.e they did not land on both heads or both did not land on tails , then we will consider such an outcome.
Let the probability of head = p
so P(head) = p
the probability of tail be = (1 - p)
This kind of probability follows a conditional distribution and the probability of getting heads is :
\(P( \{Tails, Heads\})|\{Tails, Heads,( Heads ,Tails)\})\)
\(= \dfrac{P( \{Tails, Heads\}) \cap \{Tails, Heads,( Heads ,Tails)\})}{ {P( \{Tails, Heads,( Heads ,Tails)\}}}\)
\(= \dfrac{P( \{Tails, Heads\}) }{ {P( \{Tails, Heads,( Heads ,Tails)\}}}\)
\(= \dfrac{P( \{Tails, Heads\}) } { {P( Tails, Heads) +P( Heads ,Tails)}}\)
\(=\dfrac{(1-p)*p}{(1-p)*p+p*(1-p)}\)
\(=\dfrac{(1-p)*p}{2(1-p)*p}\)
\(=\dfrac{1}{2}\)
Thus; the probability of getting heads is \(\dfrac{1}{2}\) which typically implies that the coin is fair
(b) Could we use a simpler procedure that continues to flip the coin until the last two flips are different and then lets the result be the outcome of the final flip?
For a fair coin (0<p<1) , it's certain that both heads and tails at the end of the flip.
The procedure that is talked about in (b) illustrates that the procedure gives head if and only if the first flip comes out tail with probability 1 - p.
Likewise , the procedure gives tail if and and only if the first flip comes out head with probability of p.
In essence, NO, procedure (b) does not give a fair coin flip outcome.
One number is seven less than six times another number. If the sum of the numbers is 56, find the numbers.
Answers
Answer:
The answer is 2
Step-by-step explanation:
You need to find out what is 56 divided by 6 which is 9. Then subtract, 9-7 which equals 2. So the answer is 2.
This image shows that when a football is kicked, the nearest defensive player is 6 feet from the kicker’s foot. The height of the punted football, f(x), in feet, can be modeled by the equation. Round all answers to 2 decimals. ()=−0.0152 +1.25+2 a. (2 points) What is the maximum height of the punt?
Answers
Using the vertex, it is found that the maximum height of the punt is of 27.7 feet.
The height of the punt, after x seconds, is given by:
\(f(x) = -0.0152x^2 + 1.25x + 2\)
It is a quadratic equation with coefficients \(a = -0.0152, b = 1.25, c = 2\).
The maximum value is the value of the function at the vertex, hence:
\(f_V = -\frac{\Delta}{4a} = -\frac{b^2 - 4ac}{4a}\)
Applying the coefficients:
\(f_V = -\frac{b^2 - 4ac}{4a} = -\frac{(1.25)^2 - 4(-0.0152)(2)}{4(-0.0152)} = 27.7\)
The maximum height of the punt is of 27.7 feet.
A similar problem is given at https://brainly.com/question/16858635
help fill in the chart

Answers
Amaia purchased two blouses and a skirt for a total of $32. The sales tax rate is 8%. How much total sales tax will Amaia pay on these items?
Answers
Answer:
2.56
Step-by-step explanation:
8% of 32 is 2.56
What is the probability of
spinning a yellow?
[?]%
![What is the probability ofspinning a yellow?[?]%](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/HSM7dPVeCFpwXYxAmy6pUUl1MEpRGa1T.png)
Answers
Answer:
12.5 %
Step-by-step explanation:
There are 8 total sections, and only one of them is yellow. So if we spun it eight times, the possibility of getting yellow is one time. As a result, 1/8 is 12.5%