Use the information in the table f (x), the graph g (x)and equation h (x) to evaluate the following expressions.
Drag and drop the most appropriate answer in the box provided.

Answers
Question 1
\((f \circ g)(-2)=f(-2) \cdot g(-2)=10 \cdot 3=\boxed{30}\)
Question 2
\((g \circ h)(1)=g(1) \cdot h(1)=2(1^2 -9)=\boxed{-16}\)
Question 3
\((g/f)(0)=\frac{g(0)}{f(0)}=\frac{0^2 -9}{6}=\boxed{-3/2}\)
Question 4
\((h/f)(-3)=\frac{h(-3)}{f(-3)}=\frac{3^2 -9}{12}=\boxed{0}\)
Related Questions
Salmon and Federico are choosing a number between 1 & 100, picking a color from ROY G BIV, and picking a letter out of "INDIANA". Either one will go first. State the probability of each situation as a percentage, fraction and decimal.
1. Salmon chooses a composite number, A cool color( G BIV) and an A.
2.Federico chooses a prime number, A color starting with a vowel, and a constanant.
3.Either chooses a number divisible by 7 or 8, any color, and a vowel.
4. Either chooses a number divisible by 5 or 4, blue or green, and L or N
Answers
To determine the probabilities, we need to consider the number of favorable outcomes for each situation divided by the total number of possible outcomes.
1.Probability: 228/700 = 0.3257 ≈ 32.57% ≈ 32.6% (rounded to one decimal place)
2. Probability: 200/3500 = 0.0571 ≈ 5.71% ≈ 5.7%
3. Probability: 504/2100 = 0.24 ≈ 24% (exact fraction)
4.Probability: 180/1400 = 0.1286 ≈ 12.86% ≈ 12.9% (rounded to one decimal place)
1. Salmon chooses a composite number, a cool color (G, B, I, or V), and an A:
a) Composite numbers between 1 and 100: There are 57 composite numbers in this range.
b) Cool colors (G, B, I, or V): There are 4 cool colors.
c) The letter A: There is 1 A in "INDIANA."
Total favorable outcomes: 57 (composite numbers) * 4 (cool colors) * 1 (A) = 228
Total possible outcomes: 100 (possible numbers) * 7 (possible colors) * 1 (possible letter) = 700
Probability: 228/700 = 0.3257 ≈ 32.57% ≈ 32.6% (rounded to one decimal place)
2. Federico chooses a prime number, a color starting with a vowel (E or I), and a consonant:
a) Prime numbers between 1 and 100: There are 25 prime numbers in this range.
b) Colors starting with a vowel (E or I): There are 2 colors starting with a vowel.
c) Consonants in "INDIANA": There are 4 consonants.
Total favorable outcomes: 25 (prime numbers) * 2 (vowel colors) * 4 (consonants) = 200
Total possible outcomes: 100 (possible numbers) * 7 (possible colors) * 5 (possible letters) = 3500
Probability: 200/3500 = 0.0571 ≈ 5.71% ≈ 5.7% (rounded to one decimal place)
3. Either chooses a number divisible by 7 or 8, any color, and a vowel:
a) Numbers divisible by 7 or 8: There are 24 numbers divisible by 7 or 8 in the range of 1 to 100.
b) Any color: There are 7 possible colors.
c) Vowels in "INDIANA": There are 3 vowels.
Total favorable outcomes: 24 (divisible numbers) * 7 (possible colors) * 3 (vowels) = 504
Total possible outcomes: 100 (possible numbers) * 7 (possible colors) * 3 (possible letters) = 2100
Probability: 504/2100 = 0.24 ≈ 24% (exact fraction)
4. Either chooses a number divisible by 5 or 4, blue or green, and L or N:
a) Numbers divisible by 5 or 4: There are 45 numbers divisible by 5 or 4 in the range of 1 to 100.
b) Blue or green colors: There are 2 possible colors (blue or green).
c) L or N in "INDIANA": There are 2 letters (L or N).
Total favorable outcomes: 45 (divisible numbers) * 2 (possible colors) * 2 (letters) = 180
Total possible outcomes: 100 (possible numbers) * 7 (possible colors) * 2 (possible letters) = 1400
Probability: 180/1400 = 0.1286 ≈ 12.86% ≈ 12.9% (rounded to one decimal place)
For more such questions on favorable outcomes
https://brainly.com/question/31168367
#SPJ8
Find the midpoint of the segment with the given endpoints.
(3,- 9) and (4, -8)
Answers
\(\boxed{\sf (x,y)=\left(\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2}\right)}\)
\(\\ \sf\longmapsto \left(\dfrac{3+4}{2},\dfrac{-9+8}{2}\right)\)
\(\\ \sf\longmapsto \left(\dfrac{7}{2},\dfrac{-1}{2}\right)\)
Cashews are $25.50 for 6 pounds. How much would 10 pounds cost?
Answers
Answer:
$42.50
Step-by-step explanation:
$25.50/6= 1 pound
$4.25= 1 pound
x10 x10
$42.50= 10 pounds
25.50/6
4.25/1
4.25•4= 18
25.50+18= 43.50
find the missing value 8- = -5
Answers
Answer:
x = 13
Step-by-step explanation:
call the missing number x
8 - x = - 5 Subtract 8 from both sides
8-8 - x = -5-8 Combine
-x = - 13 Multiply by -1
x = 13
What is the measure of circumscribed ∠x? 45° 50° 90° 95°
Answers
The measure of circumscribed ∠x is 90°.Hence, option (3) 90° is the correct answer.
A circumscribed angle is a vertex angle that has endpoints that lie on the circumference of a circle.
A line drawn from the vertex to the midpoint of the opposite arc (not including the vertex) is known as the angle bisector (half the length of the arc).
The length of the angle arc equals two times the length of the angle's central angle.
If the angle and its corresponding arc are named by the same letter, the phrase inscribed angle is used.
In the image below, angle ACB is a circumscribed angle that is the opposite angle of arc AB. The endpoint of the arc is at point A, and the angle's endpoint is at point C.
The angle bisector is AB, which cuts the angle in half at point D.Circle with a circumscribed angle
Given,The measure of circumscribed ∠x = ?∠x is circumscribed angle.
The angle that subtends the circle is the opposite angle of the chord that subtends it.So, the measure of the angle is twice the measure of the arc it intercepts.
∠x = 2 × 45°= 90°
Thus, the measure of circumscribed ∠x is 90°.
for such more question on circumscribed
https://brainly.com/question/2699432
#SPJ11
Write and simplify an expression for the difference between the perimeters of the figures

Answers
Answer: 4d + 6c - 6
Step-by-step explanation: The perimeter of the rectangle is the sum of all 4 sides
perimeter = 2d - 3 + 3c + 2d - 3 + 3c = 4d + 6c - 6
divide 405 in to the ratio 3:12
give answer in the form ... and ...
Answers
Answer:
81:324
Step-by-step explanation:
3+12=15
405 div 15 =27
3 times 27 = 81
12 times 27 = 324
81:324
Can someone help me or explain it bc this is rlly hard and this type of Math confuses me...

Answers
===========================================================
Explanation:
Parallel lines never cross, so we can rule out choices B, C, and D. These choices all have segments that cross or meet somehow. Segments AB and OC don't intersect, and their extended lines do not appear to intersect either.
---------
We don't really need to use a diagram for this problem even though a diagram is handy. The reason we don't need a diagram is simply look at the letters to see if there's any repeated letters.
For instance, with choice B, the letter O shows up twice. So that must mean the two segments intersect at point O. But we can't have parallel lines intersect, which allows us to rule out choice B. The other answer choices we rule out will follow the same idea.
Only AB and OC have letters that don't show up twice.
Answer:
A) AB and OC
Step-by-step explanation:
Ok, so basically, when two lines are parallel, t means they will never touch each other no matter how long they are
for example, these two l‘s are parallel
l l
in this problem, we just have to find the lines that are parallel
finsing the lines are quite easy, just look for the first letter, in this case, A, then find the other lettter, here it is B, and there is your line!
here all the lines are marked in red, whch makes finsing each line easier
proving our answer is correct...
BO and CO makes an upside down V shape ( like a roof )
CO and CD make a v Shape
and
CD and DO make an upside down L
i hope this helped!
Which equation is correct for the circle shown on the graph below?
(X+3)²+(y-6)² = 4
(x-3)²+(y+6)² = 4
(X+3)² + (y-6)² = 2
(X-3)²+(y-6)² = 4

Answers
Answer:
A
Step-by-step explanation:
the equation of a circle in standard form is
(x - h )² + (y - k )² = r²
where (h, k ) are the coordinates of the centre and r is the radius
here (h, k ) = (- 3, 6 ) and r = 2 , then
(x - (- 3) )² + (y - 6)² = 2² , that is
(x + 3)² + (y - 6)² = 4
Let a, b, p = [0, 27). The following two identities are given as cos(a + B) = cosa cosß-sina sinß, cos²p+ sin²p=1, (a) Prove the equations in (3.2) ONLY by the identities given in (3.1). cos(a-B) = cosa cosß+ sina sinß, sin(a-B)=sina-cosß-cosa sinß. Hint: sin = cos (b) Prove that as ( 27 - (a− p)) = cos((2-a) + B). sin (a-B)= cos cos²a= 1+cos 2a 2 " (c) Calculate cos(7/12) and sin (7/12) obtained in (3.2). sin² a 1-cos 2a 2 (3.1) (3.2) (3.3) (3.4) respectively based on the results
Answers
Identities are given as cos(a + B) = cosa cosß-sina sinß, cos²p+ sin²p=1,(a) cos(a+B) =cosa cosß + sina sinß (b) (27 - (a− p)) = cos((2-a) + B)=cos(2-a + B) (c) sin(7/12)cos(7/12)= (√6+√2)/4
Part (a)To prove the identity for cos(a-B) = cosa cosß+ sina sinß, we start from the identity
cos(a+B) = cosa cosß-sina sinß, and replace ß with -ß,
thus we getcos(a-B) = cosa cos(-ß)-sina sin(-ß) = cosa cosß + sina sinß
To prove the identity for sin(a-B)=sina-cosß-cosa sinß, we first replace ß with -ß in the identity sin(a+B) = sina cosß+cosa sinß,
thus we get sin(a-B) = sin(a+(-B))=sin a cos(-ß) + cos a sin(-ß)=-sin a cosß+cos a sinß=sina-cosß-cosa sinß
Part (b)To prove that as (27 - (a− p)) = cos((2-a) + B),
we use the identity cos²p+sin²p=1cos(27-(a-p)) = cos a sin p + sin a cos p= cos a cos 2-a + sin a sin 2-a = cos(2-a + B)
Part (c)Given cos²a= 1+cos2a 2 , sin² a= 1-cos2a 2We are required to calculate cos(7/12) and sin(7/12)cos(7/12) = cos(π/2 - π/12)=sin (π/12) = √[(1-cos(π/6))/2]
= √[(1-√3/2)/2]
= (2-√3)/2sin (7/12)
=sin(π/4 + π/6)
=sin(π/4)cos(π/6) + cos(π/4) sin(π/6)
= √2/2*√3/2 + √2/2*√1/2
= (√6+√2)/4
Learn more about identity here:
https://brainly.com/question/14681705
#SPJ11
if x,y ∈ N and xy=20, then find number of all possible ordered pairs (x,y)
Answers
In this instance, there are four potential ordered pairs.
We can look into the factors of 20 to determine the total number of ordered pairs (x, y) that can exist such that x, y N (natural numbers) and xy = 20.
The 20th's prime factorization is
Given that xy = 20, xy's prime factors must also be the same as those of 20.
Let's think about the potential x and y values:
x = 1, y = 20:
This pair satisfies the condition that x = 1, y = 20, and xy = 20.
x = 2, y = 10:
This pair also fulfils the equations xy = 20 and if x = 2 then y = 10.
x = 4, y = 5:
When x = 4 and y = 5, the equation xy = 20 is satisfied.
x = 5, y = 4:
If x = 5, then y = 4, and this pair satisfies xy = 20.
In total, there are four possible ordered pairs (x, y) that satisfy the condition xy = 20 and x, y ∈ N: (1, 20), (2, 10), (4, 5), and (5, 4).
Therefore, there are four possible ordered pairs in this case.
For similar question on prime factors.
https://brainly.com/question/1081523
#SPJ8
consider the results of a poll where 48% of 331 americans who decide to not go to college do so because they cannot afford it. calculate a 90% confidence interval for the proportion of americans who decide to not go to college because they cannot afford it.
Answers
The 90% confidence interval for the proportion of Americans who decide not to go to college because they cannot afford it can be calculated using a statistical formula. The formula for a confidence interval is: CI = p ± zsqrt((p(1-p))/n)
Where CI is the confidence interval, p is the proportion of interest (in this case, 0.48 or 48%), and z is the critical value from the standard normal distribution for the desired level of confidence (in this case, 1.645 for 90% confidence), sqrt is the square root function, and n is the sample size (in this case, 331).
Plugging in the values, we get:
CI = 0.48 ± 1.645sqrt((0.48(1-0.48))/331)
CI = 0.48 ± 0.062
Thus, the 90% confidence interval for the proportion of Americans who decide not to go to college because they cannot afford it is (0.418, 0.542). This means that we can be 90% confident that the true proportion of Americans who decide not to go to college because they cannot afford it falls between 41.8% and 54.2%.
To learn more about Confidence interval, visit:
https://brainly.com/question/17034620
#SPJ11
Hot dogs come in packs of 8 and hot dog buns come in packs of 6. what is the least number of hot dog packs you can buy when you want to have the same number of hot dogs and buns? how many packs of buns will you need to buy? how many total hot dogs will you have bought?
Answers
4 packs of hot dogs bun=24
That’s your answer
54 x 8181 x 12 x 8271 x 1301 x 812
Answers
Answer:
4.6320447e+16
I used a calculator for this LOL.
One little cat can eat a bag of treats in 15 minutes while another cat can eat the same bag of treats in 10 minutes. What part of the bag can they eat together in the given time? 2 minute. How about 5 minutes
Answers
1/3 of the bag would be eaten by both cats in 2 minutes while 5/6 of the bag would be eaten by both cats in 5 minutes.
What is an equation?An equation is an expression showing the relationship between numbers and variables.
One little cat can eat a bag of treats in 15 minutes while another cat can eat the same bag of treats in 10 minutes.
a) In 2 minutes:
Part of bag eaten = (1/15 minutes) * 2 minutes + (1/10 minutes) * 2 minutes = 1/3
1/3 of the bag would be eaten by both cats in 2 minutes.
b) In 5 minutes:
Part of bag eaten = (1/15 minutes) * 5 minutes + (1/10 minutes) * 5 minutes = 5/6
5/6 of the bag would be eaten by both cats in 5 minutes.
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
A rectangular tank with a square base, an open top, and a volume of 10,976 ft cubed is to be constructed of sheet steel. Find the dimensions of the tank that has the minimum surface area.
Answers
Answer:
Dimensions to minimize surface are is 28 ft x 28 ft x 14 ft
Step-by-step explanation:
The Volume of a box with a square base of say;x cm by x cm and height
h cm is;
V = x²h
Now, the amount of material used is directly proportional to the surface area, hence we will minimize the amount of material by minimizing the surface area.
The formula for the surface area of the box described is given by;
A = x² + 4xh
However, we need A as a function of
only x, so we'll use the formula;
V = x²h
V = x²h = 10,976 ft³
So,
h = 10976/x²
So,
A = x² + 4x(10976/x²)
A = x² + 43904/x
So, to minimize the area, it will be at dA/dx = 0.
So,
dA/dx = 2x - 43904/x² = 0
Factorizing out, we have;
2x³ = 43904
x³ = 43904/2
x³ = 21952
x = ∛21952
x = 28 ft
since, h = 10976/x²
h = 10976/28² = 14 ft
Thus,dimension to minimize surface are is 28 ft x 28 ft x 14 ft
Which of the following is a perfect square trinomial?
(A) 4x2 - 4x + 1
(B) 4x2 - 2x + 2
(C) 4x2 - 4x + 2
(D) 4x2 - 8x + 16
(E) 4x2 - 12x + 16
Answers
The perfect square trinomial is 4x² - 4x + 1. The correct answer would be an option (A).
What is the algebraic expression?Algebraic expressions are mathematical statements with a minimum of two terms containing variables or numbers.
The expression is given in option (A), as follows:
4x² - 4x + 1
(2x)² - 2 × 2x × 1 + 1²
Compare to the formula a² - 2 × a × b + b² = (a - b)², and we get
(2x - 1)²
Thus, this is a perfect square trinomial.
Hence, the correct answer would be an option (A).
Learn more about Expressions here:
brainly.com/question/13947055
#SPJ1
what is the center od dilation type ( Number, number)

Answers
the center of dilation for the triangle is (0,0)
Define center of dilationThe center of dilation is a point in a plane about which a dilation, a type of transformation, is performed. A dilation is a transformation that changes the size of a geometric figure, while preserving its shape and orientation. The center of dilation is the fixed point that serves as the reference for the scaling or shrinking of the figure.
In a dilation, each point of the original figure is moved away from or towards the center of dilation, by a certain factor called the scale factor.
The coordinate of yellow triangle and scaled triangle both passes through center of axes.
So, the center of dilation is (0,0).
To know more about transformation, visit:
https://brainly.com/question/11352944
#SPJ1
16. <1 and <2 form a linear pair. The
measure
of <2 is six more than twice the
of <1. Find m<2.
Answers
The measure of the angle 2 is 122°.
What is referred as the linear pair?When lines intersect at a single point, a linear pair of angles is formed. If the angles are adjacent to one another after the two lines intersect, they are said to be linear. The sum of the angles of the a linear pair will always be 180°. These angles are also referred to as supplementary angles.Given that angles 1 and 2 form a linear pair,
angle 1 + angle 2 = 180 degrees —— (1)
We've also been notified that angle 2 is 6 times the size of angle 1.
That is to say: angle 2 = (2×angle 1) + 6 ———- (2)
Putting the angle 2 value in (1) from (2)
180 = angle 1 + 2×angle 1 + 6
3×angle 1 = 174
1st angle = 58 degrees ———-(3)
(1) and (3) come from:
angle 2 + 58 = 180
2nd angle = 122 degrees
As a result, angle 2 has a measure of 122 degrees.
To know more about the linear pair, here
https://brainly.com/question/4227663
#SPJ9
w + 15 = 29
w=___ ?? HELP
Answers
Answer:
w=14
Step-by-step explanation:
29-15=14
Answer:
14
Step-by-step explanation:
29-15 =14.
The answer is 14
4.2 = c/-8.5 + 10.7
A. 55.25
B. -126.65
C. -55.25
D. 126.65
Answers
Answer: Number C
Step-by-step explanation:
Solve
1
Find common denominator
4
.
2
=
−
8
.
5
+
1
0
.
7
4.2=\frac{c}{-8.5}+10.7
4.2=−8.5c+10.7
4
.
2
=
2
−
1
7
+
−
1
7
⋅
1
0
.
7
−
1
7
4.2=\frac{2c}{-17}+\frac{-17 \cdot 10.7}{-17}
4.2=−172c+−17−17⋅10.7
2
Combine fractions with common denominator
4
.
2
=
2
−
1
7
+
−
1
7
⋅
1
0
.
7
−
1
7
4.2=\frac{2c}{-17}+\frac{-17 \cdot 10.7}{-17}
4.2=−172c+−17−17⋅10.7
4
.
2
=
2
−
1
7
⋅
1
0
.
7
−
1
7
4.2=\frac{2c-17 \cdot 10.7}{-17}
4.2=−172c−17⋅10.7
3
Multiply the numbers
4
.
2
=
2
−
1
7
⋅
1
0
.
7
−
1
7
4.2=\frac{2c{\color{#c92786}{-17}} \cdot {\color{#c92786}{10.7}}}{-17}
4.2=−172c−17⋅10.7
4
.
2
=
2
−
1
8
1
.
9
−
1
7
4.2=\frac{2c{\color{#c92786}{-181.9}}}{-17}
4.2=−172c−181.9
4
Multiply all terms by the same value to eliminate fraction denominators
4
.
2
=
2
−
1
8
1
.
9
−
1
7
4.2=\frac{2c-181.9}{-17}
4.2=−172c−181.9
−
1
7
⋅
4
.
2
=
−
1
7
⋅
2
−
1
8
1
.
9
−
1
7
-17 \cdot 4.2=-17 \cdot \frac{2c-181.9}{-17}
−17⋅4.2=−17⋅−172c−181.9
5
Cancel multiplied terms that are in the denominator
−
1
7
⋅
4
.
2
=
−
1
7
⋅
2
−
1
8
1
.
9
−
1
7
-17 \cdot 4.2=-17 \cdot \frac{2c-181.9}{-17}
−17⋅4.2=−17⋅−172c−181.9
−
1
7
⋅
4
.
2
=
2
−
1
8
1
.
9
-17 \cdot 4.2=2c-181.9
−17⋅4.2=2c−181.9
6
Multiply the numbers
−
1
7
⋅
4
.
2
=
2
−
1
8
1
.
9
{\color{#c92786}{-17}} \cdot {\color{#c92786}{4.2}}=2c-181.9
−17⋅4.2=2c−181.9
−
7
1
.
4
=
2
−
1
8
1
.
9
{\color{#c92786}{-71.4}}=2c-181.9
−71.4=2c−181.9
7
Add
1
8
1
.
9
181.9
181.9
to both sides of the equation
−
7
1
.
4
=
2
−
1
8
1
.
9
-71.4=2c-181.9
−71.4=2c−181.9
−
7
1
.
4
+
1
8
1
.
9
=
2
−
1
8
1
.
9
+
1
8
1
.
9
-71.4+{\color{#c92786}{181.9}}=2c-181.9+{\color{#c92786}{181.9}}
−71.4+181.9=2c−181.9+181.9
8
Simplify
Add the numbers
Add the numbers
1
1
0
.
5
=
2
110.5=2c
110.5=2c
9
Divide both sides of the equation by the same term
1
1
0
.
5
=
2
110.5=2c
110.5=2c
1
1
0
.
5
2
=
2
2
\frac{110.5}{{\color{#c92786}{2}}}=\frac{2c}{{\color{#c92786}{2}}}
2110.5=22c
10
Simplify
Divide the numbers
Cancel terms that are in both the numerator and denominator
Move the variable to the left
=
55.25
Answer:
A.55.25
Step-by-step explanation:
4.2 = c/-8.5 + 10.7
4.2 - 10.7 = c/-8.5
-6.5 = c/-8.5
-6.5 . -8.5 = c
55.25 = c
Suppose the force acting on a column that helps to support a building is a normally distributed random variable x with mean value 15.0 kips and standard deviation 1.25 kips. compute the following probabilities: a) p(x < 15) b) p( x < 17.5) c) p( x > 10) d) p(14 < x < 18) e) p (i x - 15 < 3)
Answers
To compute the probabilities, we can use the properties of the normal distribution and the given mean and standard deviation.
The probabilities can be determined by finding the area under the normal curve using a standard normal table or statistical software.a) To compute p(x < 15), we need to find the probability that the force acting on the column is less than 15 kips. Using the normal distribution, we can calculate the z-score (standardized score) corresponding to x = 15. With the mean μ = 15.0 kips and standard deviation σ = 1.25 kips, we can calculate the z-score as (15 - 15.0) / 1.25. Once we have the z-score, we can look up the corresponding probability in the standard normal table or use statistical software.
b) For p(x < 17.5), we follow a similar process. Calculate the z-score using the formula (17.5 - 15.0) / 1.25 and find the corresponding probability.c) To compute p(x > 10), we find the probability that the force is greater than 10 kips. Again, calculate the z-score using the formula (10 - 15.0) / 1.25 and determine the complementary probability (1 - p(x < 10)). d) For p(14 < x < 18), we calculate the probabilities of x being less than 18 (using the z-score) and less than 14. Then, subtract the probability of x being less than 14 from the probability of x being less than 18.
e) Finally, for p(|x - 15| < 3), we consider the absolute difference between x and 15. We need to find the probability that this absolute difference is less than 3. This can be calculated by finding the probabilities of x being between 12 and 18 and subtracting the complementary probabilities. By applying these steps, we can determine the probabilities based on the given mean and standard deviation of the normally distributed random variable.
To learn more about complementary probability click here:
brainly.com/question/17256887
#SPJ11
The diameter of a turbine shaft in a manufacturing facility is normally distributed, with a mean of 100 millimeters and a standard deviation of 20 millimeters. a. What is the probability of a part having a diameter of at least 130 millimeters? b. What is the probability of a part having a diameter no greater than 130 millimeters? c. What is the probability of a part having a diameter between 100 and 130 millimeters? d. What is the probability of a part having a diameter between 70 and 100 millimeters?
Answers
The probability of a part having a diameter of at least 130 millimeters is 0.1587. The probability of a part having a diameter no greater than 130 millimeters is 0.8413. The probability of a part having a diameter between 100 and 130 millimeters is 0.3413. The probability of a part having a diameter between 70 and 100 millimeters is 0.2773.
(a) The probability of a part having a diameter of at least 130 millimeters is calculated by finding the area under the standard normal curve to the right of 130. This area is 0.1587.
(b) The probability of a part having a diameter no greater than 130 millimeters is calculated by finding the area under the standard normal curve to the left of 130. This area is 0.8413.
(c) The probability of a part having a diameter between 100 and 130 millimeters is calculated by finding the area under the standard normal curve between 100 and 130. This area is 0.3413.
(d) The probability of a part having a diameter between 70 and 100 millimeters is calculated by finding the area under the standard normal curve between 70 and 100. This area is 0.2773.
The standard normal curve is a bell-shaped curve that is used to represent the probability of a standard normal variable. The standard normal variable is a variable that has a mean of 0 and a standard deviation of 1.
The probability of a part having a diameter of at least 130 millimeters is 0.1587, which means that there is a 15.87% chance that a randomly selected part will have a diameter of at least 130 millimeters.
The probability of a part having a diameter no greater than 130 millimeters is 0.8413, which means that there is an 84.13% chance that a randomly selected part will have a diameter of no greater than 130 millimeters.
The probability of a part having a diameter between 100 and 130 millimeters is 0.3413, which means that there is a 34.13% chance that a randomly selected part will have a diameter between 100 and 130 millimeters.
The probability of a part having a diameter between 70 and 100 millimeters is 0.2773, which means that there is a 27.73% chance that a randomly selected part will have a diameter between 70 and 100 millimeters.
Visit here to learn more about probability:
brainly.com/question/13604758
#SPJ11
I got the first part but i dont onow how to get the other ones

Answers
The value of x for this problem is given as follows:
x = 5.
Hence the angle measures are given as follows:
m < CAB = 32º.m < FDE = 32º.How to obtain the value of x?
We have that angles A and D are congruent for this problem, meaning that they have the same measure.
Hence the value of x is obtained as follows:
7x - 3 = 5x + 7
2x = 10
x = 5.
Hence the angle measures are given as follows:
m < CAB = 7(5) - 3 = 35 - 3 = 32º.m < FDE = 5(5) + 7 = 32º.More can be learned about angle measures at https://brainly.com/question/25716982
#SPJ1
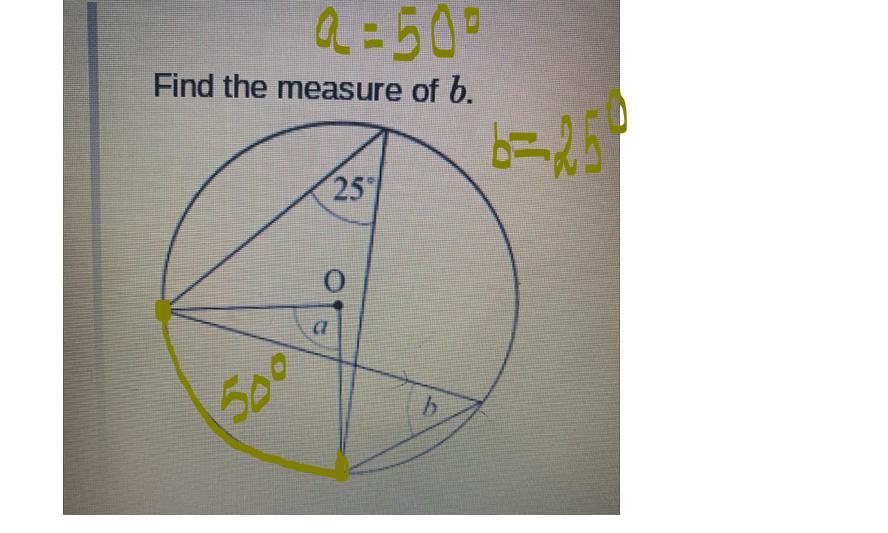
Find the measure of b.

Answers
Answer:
i'm pretty sure it's 45 degrees?
Answer:
Step-by-step explanation:
b = 25°
determine whether the series is convergent or divergent. 1/2 3/4 1/8 3/16 1/32 3/64..... convergent or divergent correct?. if it is convergent, find its sum. (if the quantity diverges, enter diverges.)
Answers
Answer: The geometric series is convergent and the value is 16.
Step-by-step explanation:
How to illustrate the information?
Recall that the sum of an infinite geometric series, S, given first term, t_1, and common ratio, r, is given by:
S = t_1/(1 - r)
Note that:
3 = (4)(3/4)
9/4 = (3)(3/4
27/16 = (9/4)(3/4)
So this a geometric series with t_1 = 4 and r = 3/4. Therefore:
4 + 3 + 9/4 + 27/16 + ... = 4/(1 - 3/4) = 4/(1/4) = 16
The correct option is 16.
Determine whether the geometric series is convergent or divergent. If it is convergent, find its sum 4+3+ 9/4 +27/16 +???
choices are
1. 3/4
2. 12
3. 4
4. divergent
5. 16
A manufacturer of chocolate chips would like to know whether its bag filling machine works correctly at the 421 gram setting. It is believed that the machine is underfilling the bags. A 21 bag sample had a mean of 417 grams with a standard deviation of 13. A level of significance of 0.1 will be used. Assume the population distribution is approximately normal. State the null and alternative hypotheses.
Answers
Null hypothesis: The bag filling machine works correctly at the 421 gram setting.
Alternative hypothesis: The bag filling machine underfills the bags at the 421 gram setting.
In hypothesis testing, the null hypothesis (H₀) represents the status quo or the belief that there is no significant difference or effect, while the alternative hypothesis (H₁) represents the claim or belief that there is a significant difference or effect.
In this scenario, the null hypothesis states that the bag filling machine works correctly at the 421 gram setting. This means that the mean weight of the bags filled by the machine is equal to 421 grams. The alternative hypothesis, on the other hand, suggests that the machine underfills the bags, indicating that the mean weight of the bags is less than 421 grams.
To determine which hypothesis is supported by the data, a hypothesis test will be conducted using the sample mean and the given level of significance. The sample mean of the 21 bag sample is 417 grams, which is lower than the hypothesized mean of 421 grams. The standard deviation of the sample is 13 grams.
The level of significance, denoted as α, is the probability of rejecting the null hypothesis when it is true. In this case, a significance level of 0.1 will be used, which means that there is a 10% chance of rejecting the null hypothesis when it is actually true.
Based on this information, the null and alternative hypotheses can be stated as follows:
Null hypothesis: The bag filling machine works correctly at the 421 gram setting (μ = 421).
Alternative hypothesis: The bag filling machine underfills the bags at the 421 gram setting (μ < 421).
The hypothesis test will involve calculating a test statistic and comparing it to a critical value or using p-values to determine the statistical significance of the results.
Learn more about Hypothesis
brainly.com/question/29576929
#SPJ11
Consider the following functions.f(x) = x^2 + 2x, g(x) = 3x^2 - 1

Answers
Explanation
The domain of a function is the set of all possible inputs for the function.
so
Let
\(\begin{gathered} f(x)=x^2+2x \\ g(x)=3x^2-1 \end{gathered}\)Step 1
a) (f+g)(x)
to add the function , add like terms
\(\begin{gathered} f(x)+g(x)=(f+g)(x)=x^2+2x+3x^2-1 \\ (f+g)(x)=x^2+2x+3x^2-1 \\ (f+g)(x)=4x^2+2x-1 \end{gathered}\)so
\(a)(f+g)(x)=4x^2+2x-1\)(b) domain of the function:
the domain of a quadratic function f(x) is the set of x -values for which the function is defined,so
\(\text{Domain:(-}\infty,\infty)\)Step 2
c) (f-g)(x)
subtract the functions
\(\begin{gathered} f(x)-g(x)=(f-g)(x)=x^2+2x-(+3x^2-1) \\ (f-g)(x)=x^2+2x-3x^2+1 \\ (f-g)(x)=-2x^2+2x+1 \end{gathered}\)d)Domain:For any linear function the domain and range are always all real numbers
\(\mleft(-\infty,\infty\mright)\)Step 3
e) (fg)(x)
\(\begin{gathered} f(x)=x^2+2x \\ g(x)=3x^2-1 \\ \text{then} \\ (fg)(x)=(x^2+2x)(3x^2-1) \\ \text{apply distributive property} \\ (fg)(x)=(x^2\cdot3x^2)-(1\cdot x^2)+(2x\cdot3x^2)-(2x\cdot1) \\ (fg)(x)=3x^4-x^2+6x^3-2x \\ \text{reorder} \\ (fg)(x)=3x^4+6x^3-x^2-2x \end{gathered}\)f) again we have a polynomial so, The domain of all polynomial functions is all real numbers:
\(\text{ Domain}\mleft(-\infty,\infty\mright)\)Step 4
g) (f/g)(x)
\(\begin{gathered} f(x)=x^2+2x \\ g(x)=3x^2-1 \\ \text{then} \\ (\frac{f}{g})(x)=\frac{(x^2+2x)}{\mleft(3x^2-1\mright)} \\ \end{gathered}\)
h) domain, we see this function is not definded when the denominator equals zero, we need to find that number
\(\begin{gathered} 3x^2-1=0 \\ \text{add 1 in both sides} \\ 3x^2-1+1=0+1 \\ 3x^2=1 \\ \text{divide both sides by 3} \\ \frac{3x^2}{3}=\frac{1}{3} \\ x^2=\frac{1}{3} \\ \sqrt{x^2}=\sqrt{\frac{1}{3}} \\ x=\frac{1}{\sqrt[]{3}} \\ so,\text{ the domain is} \\ (-\infty,\frac{1}{\sqrt[]{3}})\cup(\frac{1}{\sqrt[]{3}},\infty) \end{gathered}\)I hope this helps you
What is 2 1/2 / 2 = equal to?
Answers
Answer:
5.25
Step-by-step explanation:
21/2=10.5
10.5/2=5.25
boy can mow a lawn in 90 minutes and his sister can mow the same lawn in 60 minutes. how long will it take for both mowing at the same time to mow the lawn?
Answers
The time taken by both to mow the lawn is 36 minutes.
This is a question of time and work.
It is given that:-
Time taken by boy to mow the loan = 90 minutes.
Time taken by girl to mow the loan = 60 minutes.
We have to find the time taken by both of them together to mow the lawn.
LCM(60,90) = 180
Let the total work to be done to mow the lawn be 180 units.
Hence,
Efficiency of boy = 180/90 = 2 units
Efficiency of girl = 180/60 = 3 units
Total efficiency = 2 + 3 = 5 units.
Hence, time taken by both of them to mow the lawn = 180/5 = 36 minutes.
To learn more about time and work, here:-
https://brainly.com/question/8032605
#SPJ4