use the fundamental theorem to evaluate the definite integral exactly. 16 1 3/pi of x dx enter the exact answer. g
Answers
The exact answer to the definite integral ∫16^1^3/π of x dx using the fundamental theorem is 8/π^2.
The fundamental theorem of calculus states that if f(x) is a continuous function on the interval [a, b] and F(x) is an antiderivative of f(x), then:
∫a^bf(x)dx = F(b) - F(a)
To use the fundamental theorem to evaluate the definite integral ∫16^1^3/π of x dx, we need to find an antiderivative of x. The antiderivative of x is x^2/2 + C, where C is an arbitrary constant.
Therefore, the definite integral ∫16^1^3/π of x dx can be written as:
∫16^1^3/π x dx = (x^2/2 + C) |16^1^3/π
Evaluating this expression gives us:
(3/π)^2/2 + C - (1/π)^2/2 + C = (9/π^2 - 1/π^2)/2 + 2C
Since C is an arbitrary constant, it cancels out when we take the difference between the upper and lower limits of integration. Therefore, the definite integral ∫16^1^3/π of x dx is equal to:
(9/π^2 - 1/π^2)/2 = 8/π^2
Learn more about Integration at:
brainly.com/question/27419605
#SPJ4
Related Questions
3. Before the florist has a chance to finish the bouquets, a large order is placed. After the order, only 85 roses and 163 peonies remain. How many regular bouquets and mini bouquets can the florist make now?
Answers
Answer:
Step-by-step explanation:
does 2m, 2m, 4m make a triangle?
Answers
Answer:
No,
Step-by-step explanation:
All you have to do is use the triangle inequality therorum. if two side lengths of a triangle is always greater than the third side. you will have a triangle.
Shyla's research shows that 8 empty cans make 1/4 pound of aluminum. Shyla wants to know how many cans does it take to make 5 pounds of aluminum. How many cans are there per pound of aluminum?
Answers
Answer:
They will need 160 cans to make 5 lbs
32 cans for 1 lbs
Step-by-step explanation:
We can use ratios to solve
8 cans x cans
--------------- = ---------------
1/4 lbs 5 lbs
Using cross products
8 * 5 = 1/4x
40 = 1/4 x
Multiply each side by 4
4 * 40 = 1/4 x * 4
160 =x
They will need 160 cans to make 5 lbs
8 cans x cans
--------------- = ---------------
1/4 lbs 1 lbs
Using cross products
8 * 1 = 1/4x
Multiply each side by 4
8*4 = x
32 cans for 1 lbs
Answer:
32 cans per pound of aluminum
160 cans per 5 pounds of aluminum
Step-by-step explanation:
will make it short and simple.
8 empty cans can make 1/4 pound of aluminum.
therefore... 8 x 4 = 32 cans per pound of aluminum.
Number of cans to make 5 pounds of aluminum = 32 x 5
= 160 cans per 5 pounds of aluminum
Ten upright dominos of increasing height are lined up to be knocked down. The dominos are numbered 0 to 9. The smallest domino, #0, is 3.00 inches tall and will be toppled by a person to start the chain reaction. Each subsequent domino is 15% taller than the one before. What is the height of domino #9?
Answers
Answer:
8.604 in.
Step-by-step explanation:
We can use the formula for compound interest to find the height of domino #9:
A = P(1 + r)^n
where A is the final amount, P is the initial amount, r is the growth rate, and n is the number of compounding periods. In this case, P is the height of domino #0, r is 15% or 0.15, and n is 9 (since we want to find the height of domino #9).
Substituting the given values:
A = 3.00 in * (1 + 0.15)^9
Simplifying:
A = 3.00 in * 2.86797199
A ≈ 8.604 in
Therefore, the height of domino #9 is approximately 8.604 inches.
Ben bought a house for $102,850 and received a rebate of 15% off. He paid 6% in sales tax. How much did he save?
Answers
The required money saved is $9,256 after 6% sales tax.
Given that,
Ben bought a house for $102,850 and received a rebate of 15% off. He paid 6% in sales tax, how much did he save is to be determined.
What is simplification?
The process in mathematics to operate and interpret the function to make the function or expression simple or more understandable is called simplifying and the process is called simplification.
Here,
rebate amount = 105850 × 0.15 = $15,877
sale tax = 105850 × 0.06 = $6171
Money saved = 15, 877 - 6171 = $9,256
Thus, the required money saved is $9,256 after 6% sales tax.
Learn more about Percentage here:
https://brainly.com/question/1369388
#SPJ1
Billy took 5 tests in his math class. He scored an 89,88,93,90 and 81. What is the variance of his grades in these test? If necessary, round to the nearest hundredth.
Answers
The variance of Billy's grades obtained from his test scores is 15.76
What is variance?The variance is a measure of variability or spread a dataset. The variance can be calculated from the sum of the square of the differences of the data points from the mean divided by the number or count of the data points.
The variance of Billy's test scores can be calculated by finding the mean or the average of the scores, then finding the sum of the squares of the differences of each score from the mean as follows;
The mean score = (89 + 88 + 93 + 90 + 81)/5 = 88.2
The square of the differences of the values from the mean can be calculated as follows;
(89 - 88.2)² = 0.64, (88 - 88.2)² = 0.04, (93 - 88.2)² = 23.04, (90 - 88.2)² = 3.24, and (81 - 88.2)² = 51.84
The sum of the square of the differences is therefore;
0.64 + 0.04 + 23.04 + 3.24 + 51.84 = 78.8
The variance is therefore; 78.8/5 = 15.76Learn more on the variance of a set of data here: https://brainly.com/question/30701163
#SPJ1
Please see photo below ((:

Answers
Answer:
yo answer woud be b √5/4
Step-by-step explanation:
Sqrt(5 / 16)
Let's take the sqrt of both terms individually.
Sqrt(5) / sqrt(16) = sqrt(5) / 4
Estimate 6,976 + 3,983 + 13,560 by first rounding each number to the nearest thousand.
Answers
Answer:
Step-by-step explanation:
The thousand mark is the 4th number when going from right to left. So it would be the {6},976. When it comes to rounding, you go "5 and above, give it a shove, 4 and below, let it go. 6,976 rounded to the nearest thousand is 7,000, 3,983 rounded to the nearest thousand is 4,000, 13,560 rounded is 14,000.
7,000 + 4,000+ 14,000 = 25,000
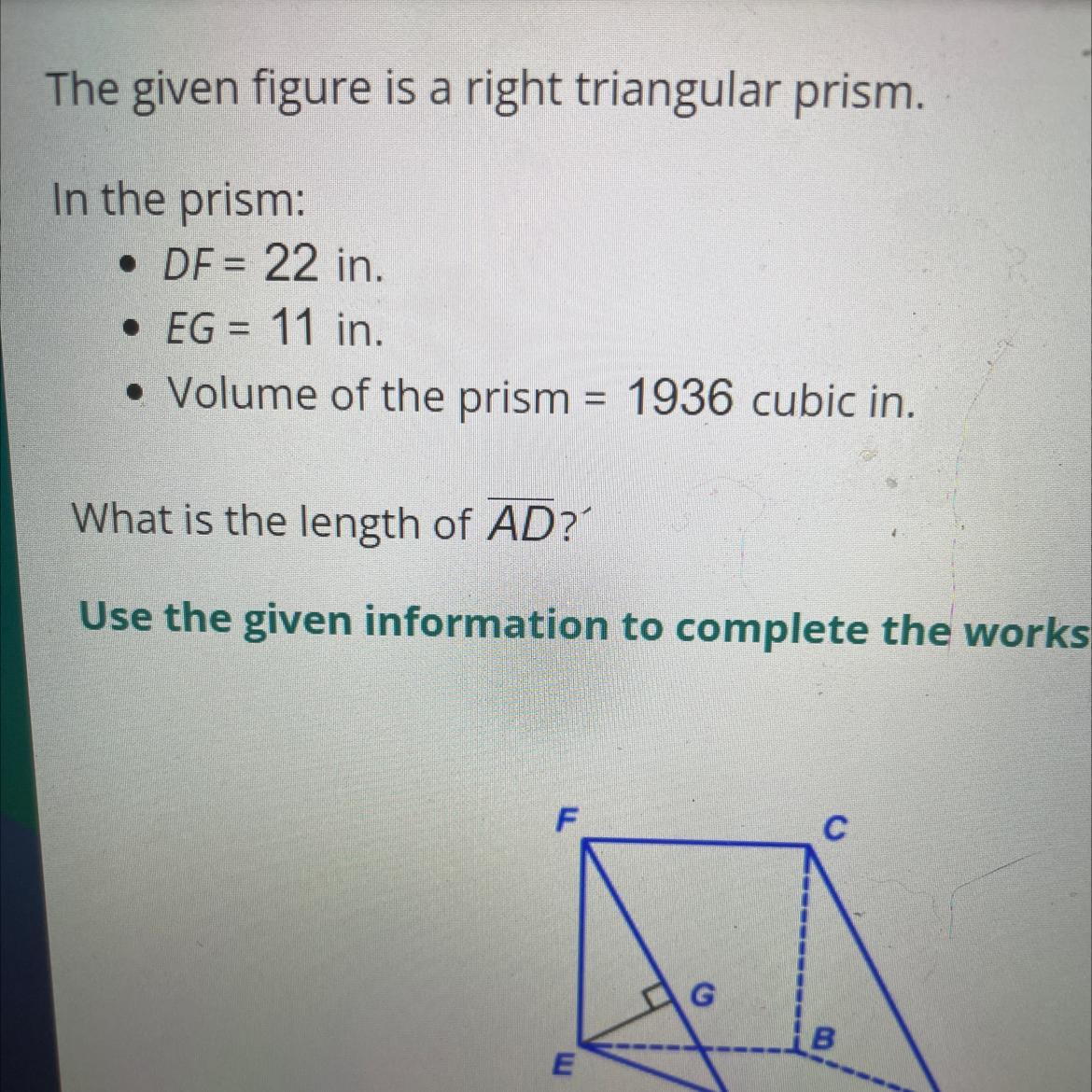
The given figure is a right triangular prism.
In the prism:
• DF = 22 in.
• EG = 11 in.
• Volume of the prism = 1936 cubic in.
What is the length of AD?'
Use the given information to complete the worksheet.
Thank you!
Answers
The length of side AD is,
⇒ AD = 16
We have to given that;
The given figure is a right triangular prism.
In the prism:
• DF = 22 in.
• EG = 11 in.
• Volume of the prism = 1936 cubic in.
Since, Volume of right triangular prism is,
V = 1/2 (bh) x L
Substitute all the values we get;
V = 1/2 (22 × 11) × AD
1936 = 121 × AD
AD = 16
Thus, The length of side AD is, 16
Learn more about the multiplication visit:
https://brainly.com/question/10873737
#SPJ1
The human body has a normal temperature of 98.6°F. Doctors will get worried if a sick patient has a temperature that varies from the normal by more than 3°F. Create an absolute value inequality and solve it to determine what body temperatures would be considered unhealthy.
Answers
Answer:
\( |T- 98.6| \geq 3\)
And in order to solve this we have two possibilities:
Solution 1
\( T -98.6 \leq -3\)
And solving for T we got:
\( T \leq 98.6- 3\)
\( T\leq 95.6\)
Solution 2
And the other options would be:
\( T -98.6 \geq 3\)
\( T \geq 101.6\)
Step-by-step explanation:
For this case we can define the variable os interest T as the real temperature and we know that if we are 3 F more than the value of 98.6 we will be unhealthy so we can set up the following equation:
\( |T- 98.6| \geq 3\)
And in order to solve this we have two possibilities:
Solution 1
\( T -98.6 \leq -3\)
And solving for T we got:
\( T \leq 98.6- 3\)
\( T\leq 95.6\)
Solution 2
And the other options would be:
\( T -98.6 \geq 3\)
\( T \geq 101.6\)
What is the distance if each path in miles?

Answers
Find the distance between the point (5,12) and the line y = 5x + 12 (rounded to the nearest hundredth).
A. 1.36 units
B. 2.19 units
C. 4.81 units
D. 4.90 units
Answers
The distance between the point (5,12) and the line y = 5x + 12 is 4.90 units
How to find the distance between a point and a line?
If a point P with the coordinates (x₁, y₁), and we need to know its distance from the line represented by ax + by + c = 0
Then the distance of a point from the line is given by the formula:
d = (ax₁ + by₁ + c) / √(a² + b²)
Given: the point (5,12) and the line y = 5x + 12. The line can be written as
5x-y+12 = 0. Thus:
x₁ = 5, y₁ = 12, a = 5, b = -1, c = 12. Substitute these into the formula:
d = (ax₁ + by₁ + c) / √(a² + b²)
d = (5×5 + (-1×12) + 12) / √(5² + (-1)²)
d = 25/√26 = 4.90 units
Therefore, the distance between the point and the line is 4.90 units. Option D is the answer
Learn more about distance between a point and a line on:
https://brainly.com/question/18276750
#SPJ1
what is the solution for 96 = 12d?
Answers
d = 8
Divide both sides of the equation by the same term
Answer:
d = 8
Step-by-step explanation:
Step 1: Divide both sides by 12.
\(12d/12 = 96/12\) \(d=8\)Therefore, the solution is 8.
What is the equation of the parabola with focus (4, 1) and directrix y = 2?
Answers
After answering the given query, we can state that the parabola equation expands upwards, and the apex is (4, 4.5).
What is equation?Using the equals sign (=) to indicate equivalence, a math equation links two statements. Algebraic equations prove the equality of two mathematical formulas through a mathematical assertion. The equal symbol, for example, puts a space between the numbers 3x + 5 and 14 in the equation 3x + 5 = 14. You can use a mathematical formula to understand the connection between the two lines that are printed on opposite sides of a letter. Most of the time, the emblem and the particular program match. e.g., 2x - 4 = 2 is an example.
P equals 1/2, meaning that the distance between the apex and the focus is equal to the distance between the directrix and the focus.
As a result, the parabola's equation is:
\((x - 4)^2 = 4(1/2)(y - 1.5)\\(x - 4)^2 = 2(y - 1.5)\)
The left half of the equation is expanded as follows: x2 - 8x + 16 = 2(y - \(1.5) x2 - 8x + 13 = 2y\\y = (1/2)x^2 - 4x + 13/2\)
The problem can also be expressed in vertex form by filling in the cube as follows:
\((x - 4)^2 = 2(y - 1.5)\\(x - 4)^2 = 2(y - 1.5) + 6\\(x - 4)^2 = 2(y - 4.5)\\(x - 4)^2/8 = (y - 4.5)\\\)
Therefore, the parabola expands upwards, and the apex is (4, 4.5).
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
x+12=23 what is the value of x
Answers
Answer:11
Step-by-step explanation:x+12=23
x=23-12
x=11
he table represents the linear function f(x), and the equation represents the linear function g(x). Compare the y-intercepts and slopes of the linear functions f(x) and g(x) and choose the answer that best describes them. x f(x) 0 1 2 11 4 21 g(x) = 4x + 1 The slope of f(x) is less than the slope of g(x). The y-intercept of f(x) is equal to the y-intercept of g(x). The slope of f(x) is less than the slope of g(x). The y-intercept of f(x) is greater than the y-intercept of g(x). The slope of f(x) is greater than the slope of g(x). The y-intercept of f(x) is equal to the y-intercept of g(x). The slope of f(x) is greater than the slope of g(x). The y-intercept of f(x) is greater than the y-intercept of g(x).
Answers
For given functions, The y-intercept of f(x) is equal to the y-intercept of g(x). The slope of f(x) is greater than the slope of g(x).
What is the definition of a function?
A function is a mathematical rule that gives each input value a distinct output value. A function is officially defined as a collection of ordered pairs (x, y) in which each input value x is coupled with exactly one output value y. The domain of the function refers to the input values, while the range refers to the output values. A graph, table, equation, or verbal explanation can all be used to depict a function. When the input value is x, the notation f(x) is commonly used to express the output value of a function f.
Now,
From given function f(x) and g(x)
For f(x) when x=0 then y=1 or y-intercept=1
for g(x), the y-intercept is 1 from equation y=4x+1
and slope of g(x)=4
and slope of f(x)=(11-1)/(2-0)
=10/5
=2
Hence,
The y-intercept of f(x) is equal to the y-intercept of g(x). The slope of f(x) is greater than the slope of g(x).
To know more about functions visit the link
brainly.com/question/12431044
#SPJ1
I NEED HELPP PLZ Which equation best represents the relationship shown in this graph?
y=−12x
y=−2x
y=12x
y = 2x

Answers
Answer:
y = 2x
the formula for linear equations are y = mx+c,
where m is the gradient,
and c is the y-intercept
to find m (the gradient):
1. pick to points on the graph (eg. -2,-4 and 2,4)
2 substitute the values into the formula for gradient y2-y1/x2-x1.
m = y2-y1/x1-x2
= -4 -4/-2-2
= -8/-4
= 2
to find c (y-intercept):
- the y-intercept is where the graph cuts the y axis
- in this graph, the y-intercept is 0
hence,
c = 0
substitute m = 2 and c = 0 to y = mx+c,
y = 2x + 0
y = 2x
hence, the equation that best represents the relationship shown in the graph is y = 2x.
A zip wire runs between two posts, 25m apart. The zip wire is at an angle of 10∘ to the horizontal. Calculate the length of the zip wire.
Answers
The length of the zip wire is approximately 25.42 meters.
To calculate the length of the zip wire, we can use trigonometry and the given information about the angle and the distance between the two posts.
Given:
Distance between the two posts: 25m
Angle of the zip wire to the horizontal: 10°
We can use the trigonometric function cosine (cos) to find the length of the zip wire. Cosine relates the adjacent side to the hypotenuse of a right triangle.
In this case, the adjacent side is the distance between the two posts (25m) and the hypotenuse is the length of the zip wire that we want to calculate.
Using the cosine function:
cos(angle) = adjacent/hypotenuse
cos(10°) = 25m/hypotenuse
To find the hypotenuse (length of the zip wire), we can rearrange the equation:
hypotenuse = 25m / cos(10°)
Using a calculator or trigonometric tables, we can find the value of cos(10°) to be approximately 0.9848.
Therefore, the length of the zip wire is:
hypotenuse = 25m / 0.9848 ≈ 25.42m
For more such questions on length
https://brainly.com/question/2217700
#SPJ8
In the square pyramid shown, points and are midpoints of the edges of one face. If the figure is sliced through points and and through the base, which best describes the shape of the resulting cross section? The picture shows a triangular prism. M and N are the points on the prism. A. rectangle B. trapezoid C. quadrilateral D. parallelogram
Answers
Based on the given information, we have a square pyramid with points M and N being the midpoints of the edges of one face. and forms a parallelogram. Option D
Since the base of the pyramid is a square, the cross section will consist of a square shape. Additionally, since the slice is made through the midpoints of the edges of the face, the resulting cross section will have parallel sides.
Considering these characteristics, we can conclude that the shape of the resulting cross section is a parallelogram. A parallelogram is a quadrilateral with opposite sides parallel. In this case, the opposite sides of the square cross section will be parallel, as the slice passes through the midpoints of the edges.
Therefore, the correct answer is D. parallelogram.
It's important to note that a triangular prism is not the correct answer because a triangular prism is a three-dimensional figure with two triangular bases and three rectangular faces. The cross section resulting from the given slice will not have the characteristics of a triangular prism. Option D.
For more such questions on midpoints visit:
https://brainly.com/question/28667736
#SPJ8
What is the length of LM if L(3,4) and M(1,-2)? Round to the nearest tenth.
A) 7.2
B) 6.0
C) 2.8
D) 6.3
Answers
Answer:
We conclude that the length of LM if L(3,4) and M(1,-2) will be:
\(d = 6.3\)
Hence, option D is correct.
Step-by-step explanation:
Given
L(3,4)M(1,-2)Determining the length of LM
(x₁, y₁) = (3, 4) (x₂, y₂) = (1, -2)The length of the distance between (x₁, y₁) and (x₂, y₂) can be determined using the formula
\(d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
substituting (x₁, y₁) = (3, 4) and (x₂, y₂) = (1, -2)
\(=\sqrt{\left(1-3\right)^2+\left(-2-4\right)^2}\)
\(=\sqrt{2^2+6^2}\)
\(=\sqrt{4+36}\)
\(=\sqrt{40}\)
\(=\sqrt{4\times 10}\)
\(=\sqrt{2^2\times \:10}\)
\(=2\sqrt{10}\)
\(=6.3\)
Therefore, we conclude that the length of LM if L(3,4) and M(1,-2) will be:
\(d = 6.3\)
Hence, option D is correct.
A researcher is exploring the notion that there is an economy of scale in raising children. While having one child might add to a family's financial stress, the second or third one might not be as "expensive" since they would already be sharing one roof, could share clothing, etc. The researcher has access to a large community of parents where 15% have one child under 18 in their home, 65% of parents have two children, and 20% of parents have three or more children. Rounded to the nearest whole number, the probability that any given family who is selected has two or more children at home is ________ %?
Answers
Answer:
The probability is \(G = 85% \)
Step-by-step explanation:
From the question we are told that
The percentage of parents that have one child under 18 in their homes is k = 15%
The percentage of parents that have two children is T = 65%
The percentage of parents that have three or more children is Y = 20%
Generally the probability that any given family who is selected have two or more children at home is mathematically evaluated as
\(G = T + Y\)
=> \(G = 65% + 20% \)
=> \(G = 85% \)
Create an image of rectangle ABCD that is
translated 6 units to the right and 3 units up
by plotting the corresponding vertices.
Plot the vertex that corresponds to A.

Answers
The image of the rectangle ABCD translated 6 units to the right and 3 units up is shown below .
In the question ,
a rectangle is given
the vertex of the rectangle ABCD is given as
A(-10,-6) , B(-10,-2) , C(-6,-2) , D(-6,-6) .
On applying the translation 6 units to right and 3 units up ,
the rule is (x,y)→(x+6,y+3)
by applying the rule for the translation
we get image as
A'(-4,-3) ,B'(-4,+1) , C'(0,1) , D'(0,-3)
The image is plotted below .
Therefore , The image of the rectangle ABCD translated 6 units to the right and 3 units up is shown below .
Learn more about Translation here
https://brainly.com/question/14285644
#SPJ1

I’ll give you 15 points if you know the answers to this question

Answers
It would be B)no.
Hope This Helps!
Restaurant A's chicken salad contains the same number of grams of fat as the chicken salad of restaurant C. Restaurant B's chicken salad contains 8 more grams of fat than restaurant A's chicken salad. If the total amount of fat in all three salads is 77 grams, find the number of grams of fat in each salad.
Restaurant A's chicken salad has grams of fat.
Restaurant B's chicken salad has grams of fat.
Restaurant C's chicken salad has grams of fat.
Answers
Answer:
Restaurant A and C: 23 grams of fat
Restaurant B: 31 grams of fat
Answer:
Restaurant A's chicken salad has 7.7 grams of fat.
Restaurant B's chicken salad has 61.6 grams of fat.
Restaurant C's chicken salad has 7.7 grams of fat.
Step-by-step explanation:
Restaurant A = C
Restaurant B = 8 × Restaurant A
Total Grams of Salad = 77
Let Reataurat A and C be x
and Reataurant B be 8x
so
A + B + C = 77
x + 8x + x = 77
2x + 8x = 77
10x = 77
x = 77 ÷ 10
x = 7.7
Restaurant A's chicken salad has 7.7 grams of fat.
Restaurant B's chicken salad has 61.6 grams of fat.
Restaurant C's chicken salad has 7.7 grams of fat.
If u want to crass check so
7.7 + 61.6 + 7.7 =
69.3 + 7.7 =
= 77
J and K are vertical angles. J and L are supplementary angles. mK=71° What is mL in degrees?

Answers
\(\large{\green{\underline{\underline{\bf{\orange{ANSWER:-}}}}}}\)
The question and data provided in the information is that (<J ≈ <K) are congruent to each other. Then (<J + <L = 180°) here supplementary means that there sum tends to 180°. And we have also provided the value of <K = 71°.
Now as per question we can write that,
\(\longrightarrow\bf{ \angle j + \angle l = 180}\)
\(\longrightarrow\bf{ \angle k + \angle l = 180 \: .... \: ( \angle j = \angle k)}\)
Now substituting values,
\(\longrightarrow\bf{71 + \angle l = 180}\)
\(\longrightarrow\bf{ \angle l = 180 - 71}\)
\(\longrightarrow\bf{ \angle l = 109}\)
The value of <L = 109°Solve the inequality (3+2x)-4>9 Express the solution in set notation.
Answers
Answer:x > 15
Step-by-step explanation:
simplify both sides of the inequality
2x + 9 > 39
subtract 9 from both sides
2x + 9 - 9 > 39 -9
2x > 30
divide both sides by 2
2x/2 > 30/2
x > 15
Brainliest please
The slope of a line is 15 and the point (3, -1) lies
on the line. Write an equation of the line in
point-slope form.
Answers
Answer:
The answer is
\( \huge y + 1 = 15(x - 3) \\ \)
Step-by-step explanation:
To find an equation of a line in point slope form when given the slope and a point we use the formula
\(y - y_1 = m(x - x_1)\)
where
m is the slope
( x1 , y1) is the point
From the question we have the final answer as
\(y + 1 = 15(x - 3)\)
Hope this helps you
In a dart game, Awasin and Tally each threw the darts 10 times. Tally
had three (+2) scores, three (-3) scores and four (+1) scores. Awasin had
four (+2) scores, four (-3) scores, and two (+1) scores. The winner had the
greater score. Who won the game and what was their score?
Answers
Tally won the dirt throwing game and his score was 1.
What is a numerical expression?A numerical expression is a mathematical statement written in the form of numbers and unknown variables. We can form numerical expressions from statements.
From the given information, The score of Tally is,
= 3×2 - 3×3 + 4×1.
= 6 - 9 + 4.
= 1.
The score of Awasin is,
= 4×2 - 4×3 + 2×1.
= 8 - 12 + 2.
= - 2.
So, Tally won the game and his score is 1.
learn more about numerical expressions here :
https://brainly.com/question/29199574
#SPJ1
Write an expression without brackets that is equivalent to (2x)2
Answers
Answer:
\(4 {x}^{2} \)Step-by-step explanation:
As,
\( {(ax)}^{2} = a \times a \times x \times x\)
Hence,
\( {(2x)}^{2} \)
= 2×2×x×x
\( = 4 {x}^{2} (ans)(without \: brackets)\)
I think ???
But (2✖️)2 is no an expression because can’t calculator
what equation is equivalent to 2^3^x =10
Answers
Answer:
\(log_2(10)\)
how to findSimplify the equation using logarithms.
part 1\(2^3x=10\)
\(log_1_0(2^3x)=log_1_0(10)\)
log rule ⇩
\(log_a(x^y)=y*log_a(x)\)
move exponent out of log.
\(x*log_1_0(2)=log_1_0(10)\)
part 2isolate variable further
\(x*log_1_0(2)=log_1_0(10)\)
\(x=\frac{log_{10}(10)}{log_{10}(2)}\)
formula for combining logs. ⇩
\(\frac {log_b(x)}{log_b(a)}=log_a(x)\)
the result ⇩
\(x=log_2(10)\)