Answers
Step-by-step explanation:
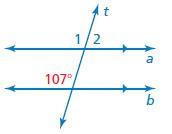
The given angle is 107°;
Since the lines given are parallel and a transversal cuts them, angle 1 and 107° are corresponding angles.
Corresponding angles are equal;
So, ∠1 = 107°;
Now, ∠1 and ∠2 are angles on a straight line;
∠1 + ∠2 = 180°
107° + ∠2 = 180°
∠2 = 180° - 107° = 73°
Answer: <1= 107 <2=73
Step-by-step explanation: Zigzag method for <1
<1+<2=180
180-<1=<2
180-107=73
Related Questions
Wynona buys some new boots that are priced $85. 79. She gets successive discounts of 10% followed by 5% off on the boots. The purchase price of Wynona’s boots is _____ of the original price. A. 84% b. 84. 5% c. 85% d. 85. 5%.
Answers
The purchase price of Wynona’s boots is 85.5% of the original price.
It is given that
The marked price of boots = $85.79
What is the percentage?The percentage is a relative value indicating the hundredth parts of any quantity.
Price after a discount of 10% = \(85.79 - 85.79*10/100 = 77.211\)
Price after another discount of 5% = \(77.211-77.211*5/100 = 73.35\)
\(\frac{PurchasePrice}{OriginalPrice}*100 =\frac{73.35}{85.79}*100 = 85.5\)
Therefore, The purchase price of Wynona’s boots is 85.5% of the original price.
To get more about percentage visit:
https://brainly.com/question/24304697
Evaluate each of the following definite integrals exactly through an appropriate u-substitution. (a) ^1_1 x/1 + 4x^2dx (b) ^1_0 e^-x(2e^-x+3)^9dx (c) ^4/pi_2/pi cos(1/x)/x^2dx
Answers
-π/2
(a) To evaluate this definite integral, we will use the u-substitution method. Let u = 1 + 4x^2, then du = 8x dx.
Therefore, the definite integral becomes:
∫^1_1 x/1 + 4x^2dx = ∫^1_1 (1/8) du = (1/8)(u|^1_1) = (1/8)(1 + 4x^2|^1_1) = (1/8)(1 - 1) = 0
(b) To evaluate this definite integral, we will use the u-substitution method. Let u = 2e^-x + 3, then du = -2e^-x dx.
Therefore, the definite integral becomes:
∫^1_0 e^-x(2e^-x+3)^9dx = ∫^1_0 (-1/2)u^9 du = (-1/2)(u^10|^1_0) = (-1/2)((2e^-x+3)^10|^1_0) = (-1/2)((2e^-x+3)^10 - 1)
(c) To evaluate this definite integral, we will use the u-substitution method. Let u = 1/x, then du = -1/x^2 dx.
Therefore, the definite integral becomes:
∫^4/pi_2/pi cos(1/x)/x^2dx = ∫^4/pi_2/pi (-1/u^2) du = (-1/u|^4/pi_2/pi) = (-1/(1/x|^4/pi_2/pi)) = (-1/(4/π - 2/π)) = (-1/(2/π)) = -π/2
Learn more about u-substitution method
brainly.com/question/17081984
#SPJ11
please answer thankyou in advanced

Answers
Answer:
15.3cm^2
Step-by-step explanation:
Area
a = (b1 + b2)/2 * h
a = (2 + 7)/2 * 3.2
a = 9/2 * 3.2
a = 15.3
A 17.0-m-high and 11.0-m-long wall and its bracing under construction are shown in the figure. 17.0m 8.5 m 10 braces Calculate the force, in newtons, exerted by each of the 10 braces if a strong wind exerts a horizontal force of 645 N on each square meter of the wall. Assume that the net force from the wind acts at a height halfway up the wall and that all braces exert equal forces parallel to their lengths. Neglect the thickness of the wall. Grade Summary sin o cos tan o a tan a cotan sin h cos h tan h cotan h Degrees O Radians V
Answers
Therefore, each of the 10 braces exerts a force of approximately 6035.25 N.
To calculate the force exerted by each of the 10 braces, we need to consider the horizontal force exerted by the wind and the geometry of the wall and bracing.
Given:
Height of the wall (h) = 17.0 m
Length of the wall (l) = 11.0 m
Number of braces (n) = 10
Horizontal force exerted by the wind (F_w) = 645 N/m^2
First, let's calculate the total area of the wall:
Wall area (A) = h * l = 17.0 m * 11.0 m = 187.0 m^2
Since the net force from the wind acts at a height halfway up the wall, we can consider the force acting on the top half of the wall:
Force on the top half of the wall (F_t) = F_w * (A/2) = 645 N/m^2 * (187.0 m^2 / 2) = 60352.5 N
Next, let's calculate the force exerted by each brace:
Force exerted by each brace (F_brace) = F_t / n = 60352.5 N / 10 = 6035.25 N
Learn more about approximately here:
https://brainly.com/question/31695967
#SPJ11
good evening! Can someone please answer this, ill give you brainliest and your earning 50 points. Would be very appreciated.
the last row is 9

Answers
Solution:
In the table, we can see that as each round pass, the number of games is being halved.
This means that:
⇒ Round 4 = (Round 3)/2 = 16/2 = 8 games⇒ Round 5 = (Round 4)/2 = 8/2 = 4 games⇒ Round 6 = (Round 5)/2 = 4/2 = 2 gamesHence, in round six, two games will be played.
Answer:
2
Step-by-step explanation:
In the first round, the 128 teams played 64 games. Then in the second round, the 64 teams left played 32 games. That left 32 teams to play 16 games in the third round.
So it is a simple elimination format with number of games going down by half after each round.
4th round: 8 games
5th round: 4 games
6th round: 2 games
Find the value of x that makes 25x^2 + 70x + c a perfect square trinomial
Answers
The value of x that makes 25x^2 + 70x + c a perfect square trinomial is c = 1225.
To make the quadratic expression 25x^2 + 70x + c a perfect square trinomial, we need to determine the value of c.
A perfect square trinomial can be written in the form (ax + b)^2, where a is the coefficient of the x^2 term and b is half the coefficient of the x term.
In this case, a = 25, so b = (1/2)(70) = 35.
Expanding (ax + b)^2, we have:
(25x + 35)^2 = 25x^2 + 2(25)(35)x + 35^2
= 25x^2 + 70x + 1225.
Comparing this with the given quadratic expression 25x^2 + 70x + c, we can see that c = 1225.
Know more about quadratic expression here:
https://brainly.com/question/31368124
#SPJ11
The sum of the squares of two consecutive even integers is 1684. Find the integers.
Answers
The possible values of two consecutive even integers, of which the sum of their squares is 1684, are 28 and 30 for positive integers, while for negative integers, they are -28 and -30.
The difference between two consecutive even integers is 2.
Let the integers be a and (a+2). Then,
a² + (a + 2)² = 1684
a² + a² + 4a + 4 = 1684
2a² + 4a - 1680 = 0
a² + 2a -840 = 0
Hence, we get a quadratic equation.
There are three methods of solving a quadratic equations: by factoring, completing the square, and by using the abc formula.
Use the factoring method:
a² + 2a -840 = (a - 28) (a + 30)
a = 28 and a = -30
Hence, if the integers are positive, they are: 28 and 30.
If the integers are negative, they are -28 and -30.
Learn more about quadratic equation here:
https://brainly.com/question/30164833
#SPJ4
F x a
If F = 48 when a = 4 find,
F when a = 5
F =
Answers
7) Complete the blanks in this bank statement.
Date
25/03/20
28/03/20
29/03/20
Income Outgoings Balance
£453
£1200
£957

Answers
Using the arithmetic operations the balance amount for 28/03/20 and incoming amount for 29/03/20 is obtained as £ 747 and £ 210 respectively.
What is arithmetic operation?
A subject of mathematics known as arithmetic operations deals with the study and use of numbers in all other branches of mathematics. Basic operations including addition, subtraction, multiplication, and division are included.
The statement of bank account is given.
On 25/03/20 the balance amount left in bank was £ 1200.
On 28/03/20 the outgoing amount from the bank was £ 453.
To find the balance amount for 28/03/20, use the arithmetic operation of subtraction -
Balance amount = Previous Balance - Outgoing Amount
Substitute the values in the equation -
Balance amount = 1200 - 453
Balance amount = 747
Therefore, the balance amount for 28/03/20 was £ 747.
Now, On 29/03/20 the balance amount left in bank was £ 957.
To find the incoming amount for 29/03/20, use the arithmetic operation of subtraction -
Incoming Amount = New Balance - Previous Balance
Incoming Amount = 957 - 747
Incoming Amount = 210
Therefore, the incoming amount for 29/03/20 was £ 210.
To learn more about arithmetic operation from the given link
https://brainly.com/question/20628271
#SPJ1

In δabc, ab = x, bc = y, and ca = 2x. a similarity transformation with a scale factor of 0.5 maps δabc to δmno, such that vertices m, n, and o correspond to a, b, and c, respectively. if om = 5, what is ab? a. ab = 2.5 b. ab = 10 c. ab = 5 d. ab = 1.25 e. ab = 2
Answers
The value of ab in the similarity transformation from triangle abc to triangle mno is 5
How to determine the value of ab?The given parameters are:
ab = x, bc = y, and ca = 2x
om = 5
The scale factor from abc to mno is 0.5.
So, we have:
0.5 * ca = om
Substitute om = 5
0.5 * ca = 5
Divide both sides by 0.5
ca = 10
Recall that:
ca = 2x
So, we have:
2x = 10
Divide by 2
x = 5
Recall that:
ab = x
So, we have:
ab = 5
Hence, the value of ab is 5
Read more about similarity transformation at:
https://brainly.com/question/26836817
#SPJ4
50,60,72 find the 8th term airthmetic and geometric sequence
Answers
Answer:
8th term is 179.15904
Step-by-step explanation:
The sequence is geometric with a common ration = 6/5
r = 60/50 = 72/60 = 6/5
Use the formula
\(a_{n} = ar^{n - 1}\)
In your case a = 50, r = 6/5 and n = 8
\(a_{8} = 50(6/5)^{8 - 1} \\ = 50(6/5)^{7} \\ = 50(279936/78125)\\ = 179.15904\)
Question 7(Multiple Choice Worth 1 points)
(01.05 MC)The total charge on 4 particles is -36 units. All the particles have the same charge.
What is the charge on each particle?
0-9 units
-8 units
08 units
9 units
Answers
Answer:
-9 units
Step-by-step explanation:
\( - \frac{36}{4} = - 9 \\ \)
Is the vertical component of velocity ever zero? If so, where?
Answers
The vertical component of velocity can be zero at specific points in the motion of an object.
What is Velocity?
Velocity is a vector quantity that describes the rate of change of an object's position in space over time. It is defined as the displacement of an object divided by the time interval during which the displacement occurred.
The vertical component of velocity can be zero at specific points in the motion of an object. This occurs when the object reaches the highest point in its vertical motion and begins to fall back down. At this point, the vertical component of velocity changes direction from upward to downward, and its magnitude becomes zero. This moment is known as the "instant of maximum height" or "instant of maximum altitude." Beyond this point, the vertical component of velocity becomes negative, indicating that the object is moving downward.
To learn more about Velocity, Visit
https://brainly.com/question/80295
#SPJ4
In the right triangle ABC, CD is an altitude, and c=e+f,by combining three equations it can be shown that a^2+b^2=c^2.One of the equations is c=e+f.which of the following could be the other two equations
Answers
Answer:
Please provide a diagram as the question is confusing.
What did the animals proceed to destroy after the animals had run out Mr and Mrs Jones?
Answers
Long after Mr. and Ms. Jones has been destroyed from the farm, the animals called pigs invoke his name to scare the other animals into submission.
Indeed though the ranch possesses all of the necessary accoutrements to make the windmill, but the design presents a number of difficulties.
The creatures in the farm are struggle over how to break the available gravestone into manageable sizes for structure without picks and crowbars, which they're unfit to use.
And they eventually break the problem by learning to raise and also drop big monuments into the chase, smashing them into usable gobbets.
At the time of late summer, the creatures have enough broken gravestone to begin construction.
To know more about structure here
https://brainly.com/question/28086079
#SPJ4
What is the equation of the line with slope 4 and y-intercept (0, -1)? (Final answer should be in standard form.)
Answers
Answer:
The answer is 4x - y = 1
The mean exam score for 49 male high school students is 239 and the population standard deviation is 47 The mean exam score for 53 female high school students is 21.1 and the population standard deviation is 4.3. At α=001, can you reject the claim that male and female high school students ha equal exam scores? Complete parts (a) through (e). Click here to view page 1 of the standard normal distribution table. Click here to view. page 2 of the standard normal distribution table. A. Male high school students have lower exam scores than female students B. Male and temale high school students have different exam scores. C. Male and female high school students have equal exam scores D. Male high school students have greater exam scores than female students
Answers
Comparing the means of the two samples, we find that the difference between the means is significant. Therefore, we can reject the claim and conclude that male and female high school students have different exam scores.
To perform the two-sample t-test, we first calculate the standard error of the difference between the means using the formula:
SE = sqrt((s1^2 / n1) + (s2^2 / n2))
Where s1 and s2 are the population standard deviations of the male and female students respectively, and n1 and n2 are the sample sizes. Plugging in the values, we have:
SE = sqrt((47^2 / 49) + (4.3^2 / 53))
Next, we calculate the t-statistic using the formula:
t = (x1 - x2) / SE
Where x1 and x2 are the sample means. Plugging in the values, we have:
t = (239 - 21.1) / SE
We can then compare the t-value to the critical t-value at α = 0.01 with degrees of freedom equal to the sum of the sample sizes minus 2. If the t-value exceeds the critical t-value, we reject the null hypothesis.
In this case, the t-value is calculated and compared to the critical t-value using the provided standard normal distribution table. Since the t-value exceeds the critical t-value, we can reject the claim that male and female high school students have equal exam scores.
Therefore, the correct answer is:
B. Male and female high school students have different exam scores.
Learn more about hypothesis testing here: brainly.com/question/17099835
#SPJ11
Evaluate the double integrals by first identifying it as a volume of a solid.
double integral (4-2y)dA, R=[0,1] X [0,1]
Answers
The value of the double integral is 3. This represents the volume of a solid under the surface defined by z = 4-2y and above the rectangle R in the xy-plane with limits [0,1] x [0,1].
To evaluate the double integral and identify it as a volume of a solid, we'll first rewrite the given integral using proper notation and then evaluate it.
Given integral: ∬R (4-2y) dA, R = [0,1] x [0,1]
Since R is a rectangle in the xy-plane with limits [0,1] x [0,1], we can rewrite the integral as:
∬R (4-2y) dA = ∫(from 0 to 1) ∫(from 0 to 1) (4-2y) dx dy
Now, we will evaluate the inner integral with respect to x:
∫(from 0 to 1) [(4-2y)x] (from 0 to 1) dy = ∫(from 0 to 1) (4-2y) dy
Next, we will evaluate the outer integral with respect to y:
∫(from 0 to 1) (4-2y) dy = [4y - y²] (from 0 to 1) = (4(1) - (1)²) - (4(0) - (0)²) = 3
So, the value of the double integral is 3. This represents the volume of a solid under the surface defined by z = 4-2y and above the rectangle R in the xy-plane with limits [0,1] x [0,1].
To learn more about double integral here:
brainly.com/question/29754607#
#SPJ11
a dart board is a regular octagon divided into regions as shown. suppose that a dart thrown at the board is equally likely to land anywhere on the board. what is the probability that the dart lands within the center square?
Answers
The probability that the dart lands in centre is = √2-1.
What is probability?The area of mathematics known as probability deals with numerical representations of the likelihood that an event will occur or that a statement is true.An event's probability is a number between 0 and 1, where, roughly speaking, 0 denotes the event's impossibility and 1 denotes certainty.The likelihood that an event will occur increases with its probability.A straightforward illustration is tossing a fair (impartial) coin.The chance of both outcomes ("heads" and "tails") is equal because the coin is fair, "heads" is more likely than "tails," there are no other conceivable outcomes, and the likelihood of either outcome is half.acc to our question-,
Let the side of octagon be rexterior angle of octagon = 360/8 = 45So interior angle = 180 -45 = 135So all the triangles will have 45-90-45 combinationsc sides of triangles = r/2√r/2 Calculate the total area of octagon and the area of central squareProbability = area of square /area of octagon = r2/(r2+r2+22√+r2)r2/(r2+r2+22+r2)= 1/(2+22√)take 2 common and multiply and divide byhence,The probability that the dart lands in centre is = √2-1.
learn more about probability click here:
brainly.com/question/13604758
#SPJ4
Find all solutions to 2 sin() 1 on the interval 0"
Answers
The solutions to the equation 2sin(θ) = 1 on the interval [0, 2π) are:
θ = π/6, 13π/6
To find all solutions to the equation 2sin(θ) = 1 on the interval [0, 2π), we can solve for θ by isolating the sin(θ) term and then using inverse trigonometric functions.
Given: 2sin(θ) = 1
Dividing both sides by 2:
sin(θ) = 1/2
Now, we can use the inverse sine function to find the solutions:
θ = sin^(-1)(1/2)
The inverse sine of 1/2 is π/6. However, we need to consider all solutions on the interval [0, 2π).
Since the sine function has a period of 2π, we can find the other solutions by adding integer multiples of 2π to the principal solution.
The principal solution is θ = π/6. Adding 2π to it, we get:
θ = π/6 + 2π = π/6, 13π/6
So, the solutions to the equation 2sin(θ) = 1 on the interval [0, 2π) are:
θ = π/6, 13π/6
These are the two solutions that satisfy the given equation on the specified interval.
Learn more about trigonometric functions here:
https://brainly.com/question/28483432
#SPJ11
Find the radius of convergence, R, of the series.
a. [infinity] b. sum.gif
c. n = 1
d. x^n
e. n^43^n
Answers
R = 1/3.
a. R = Does not converge
b. R = Cannot be determined without knowing the value of sum.gif
c. R = 1
d. R = 1
e. R = 1/3
To find the radius of convergence, R, of the series, we need to use the ratio test. The series is given by:
sum(n=1 to infinity) of a_n
where a_n is given by:
a_n = x^n * n^43^n
Applying the ratio test, we get:
lim (n → ∞) |a_n+1 / a_n| = lim (n → ∞) |x^(n+1) * (n+1)^43 * 3^(n+1) / (x^n * n^43 * 3^n)|
= lim (n → ∞) |x * (n+1)^43 * 3 / n^43|
= |x| * lim (n → ∞) ((n+1)/n)^43
= |x|
The series converges if the limit is less than 1 and diverges if the limit is greater than 1. Therefore, we need to solve the inequality |x| < 1 to find the radius of convergence, R.
a. If x = infinity, then the series diverges.
b. If x = sum.gif, then the series converges if |sum.gif| < 1. We cannot simplify this expression further without knowing the value of sum.gif.
c. If x = 1, then the series becomes:
sum(n=1 to infinity) of n^43
This is a p-series with p = 43 > 1, which converges. Therefore, R = 1.
d. If x = -1, then the series becomes:
sum(n=1 to infinity) of (-1)^n * n^43
This is an alternating series with decreasing terms. We can apply the alternating series test to show that it converges. Therefore, R = 1.
e. If x = 3, then the series becomes:
sum(n=1 to infinity) of n^43 * 3^n
This is a geometric series with a common ratio r = 3 > 1. Therefore, the series diverges.
Find more about geometric series
brainly.com/question/31983483
#SPJ11
Suppose you are designing a plant that treats 0.3 m3/s. The plant uses two parallel flocculation basins, each 12 m long (total) x 4 m wide with a 4 m water depth. What is the overall time (min) required for the flocculation step
Answers
According to the given statement the overall time required for the flocculation is approximately 10.67 minutes.
To calculate the overall time required for the flocculation step, we need to use the formula:.
Overall Time = Total Volume / Flow Rate
First, we need to find the total volume of the two parallel flocculation basins.
Total Volume = Length x Width x Depth x Number of Basins
Since there are two basins, the length of each basin is 12 m.
The width is 4 m, and the water depth is also 4 m.
Total Volume = (12 m + 12 m) x 4 m x 4 m = 192 m³
Next, we need to convert the flow rate from m³/s to m³/min.
Flow Rate = 0.3 m³/s x 60 s/min = 18 m³/min
Finally, we can calculate the overall time by dividing the total volume by the flow rate.
Overall Time = Total Volume / Flow Rate = 192 m³ / 18 m³/min ≈ 10.67 min
To know more about flocculation visit;
https://brainly.com/question/31491406
#SPJ11
The overall time required for the flocculation step in this plant is approximately 10.67 minutes. This means it takes approximately 10.67 minutes for the water to pass through the two parallel flocculation basins.
To calculate the overall time required for the flocculation step, we need to consider the hydraulic detention time in the flocculation basins. The hydraulic detention time is the average time it takes for water to pass through the flocculation basins.
First, let's calculate the volume of water that can be held in the basins:
Volume = length × width × depth = 12 m × 4 m × 4 m = 192 m³
Since the plant treats 0.3 m³/s, we can calculate the hydraulic detention time:
Hydraulic Detention Time = Volume / Flow Rate = 192 m³ / 0.3 m³/s = 640 s
Now, let's convert this time to minutes:
Overall Time = Hydraulic Detention Time / 60 = 640 s / 60 = 10.67 min (rounded to two decimal places)
Learn more about hydraulic detention
https://brainly.com/question/31734806
#SPJ11
How many 7 feet are in 1,645
Answers
Answer: 53 feet?
Step-by-step explanation:
Given that ∠2 ≅ ∠6.
Which theorem proves that line d is parallel to line e.
Alternate interior angle theorem
Converse of the alternate interior angle theorem
Alternate Exterior angle theorem
Converse of the alternate exterior angle theorem

Answers
Answer:
Converse of the alternate exterior angle theorem
Step-by-step explanation:
just took the test ;)
The theorem that proves that lines d and e are parallel to each other, given that <2 is congruent to <6 is: D. Converse of the alternate exterior angle theorem
When a transversal cuts across two parallel lines, there are special angles formed having relationship with each other.
For two lines to be parallel, such relationship must exist. That is what a converse theorem seeks to prove.
We are told that <2 is congruent to <6.Both angles are exterior angles that also lie opposite each other along the transversal. That makes them alternate exterior angles.<2 will be congruent to <6 if lines d and le are parallel to each other.Therefore, the theorem that proves that lines d and e are parallel to each other, given that <2 is congruent to <6 is: D. Converse of the alternate exterior angle theorem
Learn more here:
https://brainly.com/question/10565830
Does anyone know the answer to this problem?

Answers
Answer:
B to C: 1
C to D: 0
G to H: 2.5
Step-by-step explanation:

A traffic light runs repeatedly through the following cycle: green for 30 seconds, then yellow for 3 seconds, and then red for 30 seconds. Leah picks a random three-second time interval to watch the light. What is the probability that the color changes while she is watching
Answers
The probability that the colour changes, while she is watching, is 1/7
Concept: Event probability = number of favorite results /Total number of results
It is given that the traffic light runs repeatedly in the following time cycle: green for 30 seconds, then yellow at 3 seconds, and then red for 30 seconds.
This means that the traffic light passes through 63 seconds to complete one-time cycle.
It is also given that Leah chooses a random 3 second time interval to watch the light.
We should find the probability that the color changes while Leah is looking.
The green light will change after 30 seconds and after three seconds it will change to yellow light, that is at 33 second it is yellow and after another 30 seconds it will change to red light.
Now let time t=0
The light changes at three different times: t=30,t = 33 and t = 63
This means that the light will change if Leah watches at intervals [27,30]
, [30,33] or [60,63]
Since each interval is 3 seconds and there are 3 intervals, Leah will have a chance of 9 seconds.
That makes a total of 9 seconds out of 63
⇒Probability that Leah watches the color change=Number of seconds she watches/Total seconds
=9/63=17
∴ The probability that Leah observes the color change is 1/7
For more information about probability, visit https://brainly.com/question/24756209
#SPJ4
A car speed increases from 40 km/hr to km/hr in 5 sec. Calcuate the acceleration of car:
Answers
Answer:
14400km/h
Step-by-step explanation:
Given that
The speed of the car increased from 40 km/hr to 60 km/hr
And, the time taken is 5 seconds
we need to find out the acceleration of the car
So,
Here
u = initial velocity =40km/h
v = final velocity =60km/h
t = time = 5s =5 ÷ 3600h
a = acceleration
Now as we know that
a = (v - u) ÷ t
= (60 - 40) ÷ (5 ÷ 3600)
= (20 × 3600) ÷ 5
= 14400km/h
-12x + 2 y = 8
-6x + y = -3
Answers
Answer:
I'll give you the answer. This is system of equations, yes?
I WILL GIVE BRAINIEST, PLEASE HELP


Answers
Answer:
A = (1, 10)
B = (4,10)
C = (4, 14)
D = (1, 16)
Step-by-step explanation:
Okay, so first, we move, or translate the quadrilateral PQRS down -8 spaces on the graph, turning old points:
P (1, -2) = (1, -10) Q (4, -2) = (4, - 10) S (1, -8) = (1, -16) and R (4, -6) = (4, -14)
Now, we need to rotate this new box into -x, y. So our new points are:
(1, -10) = (-1, 10) (4, -10) = (-4, 10) (1, -16) = (-1, 16) and (4,-14) = (-4, 14)
Now we're reflecting off the y-axis, making our x change. So for our final points:
A(1, 10) B (4,10) D(1, 16) and C(4, 14)
Hope this helps! Please check my math and comment wether this worked or not! :)
Answer:
hi
Step-by-step explanation:
consider the differential equation y '' − 2y ' 26y = 0; ex cos(5x), ex sin(5x), (−[infinity], [infinity]).Verify that the given functions form a fundamental set of solutions of the differential equation on the indicated interval
Answers
The given function satisfies the differential equation.Therefore, the given functions ex cos(5x) and ex sin(5x) form a fundamental set of solutions of the differential equation y'' - 2y' + 6y = 0 on the interval (−∞, ∞).
Given Differential Equation: y'' - 2y' + 6y
= 0Let's substitute the given function ex cos(5x) to the differential equation:y'' - 2y' + 6y
= 0 Differentiating y'' with respect to x:dy''/dx
= -25ex cos(5x) + 10ex sin(5x) dy''/dx
= (5.25) ex cos(5x) + 25ex sin(5x)Substituting these values, we get the following:y'' - 2y' + 6y
= (-25) ex cos(5x) + 10ex sin(5x) - 2(5ex sin(5x)) + 6ex cos(5x)
= (5.25ex cos(5x) + 25ex sin(5x)) - (10ex sin(5x) + 10ex sin(5x)) + 6ex cos(5x)
= ex cos(5x)(5.25 - 2 + 6) + ex sin(5x)(25 - 10 - 10)
= 9.25 ex cos(5x) + 5 ex sin(5x)The given function satisfies the differential equation.Now, let's substitute ex sin(5x) into the differential equation:y'' - 2y' + 6y
= 0 Differentiating y'' with respect to x:dy''/dx
= 25ex sin(5x) + 10ex cos(5x) dy''/dx
= (5.25) ex sin(5x) - 25ex cos(5x)Substituting these values, we get the following:y'' - 2y' + 6y
= (25) ex sin(5x) + 10ex cos(5x) - 2(25ex cos(5x)) + 6ex sin(5x)
= (5.25ex sin(5x) - 25ex cos(5x)) - (20ex cos(5x) - 10ex cos(5x)) + 6ex sin(5x)
= ex sin(5x)(5.25 + 6) + ex cos(5x)(10 - 20)
= 11.25 ex sin(5x) - 10 ex cos(5x).The given function satisfies the differential equation.Therefore, the given functions ex cos(5x) and ex sin(5x) form a fundamental set of solutions of the differential equation y'' - 2y' + 6y
= 0 on the interval (−∞, ∞).
To know more about fundamental visit:
https://brainly.com/question/32742251
#SPJ11