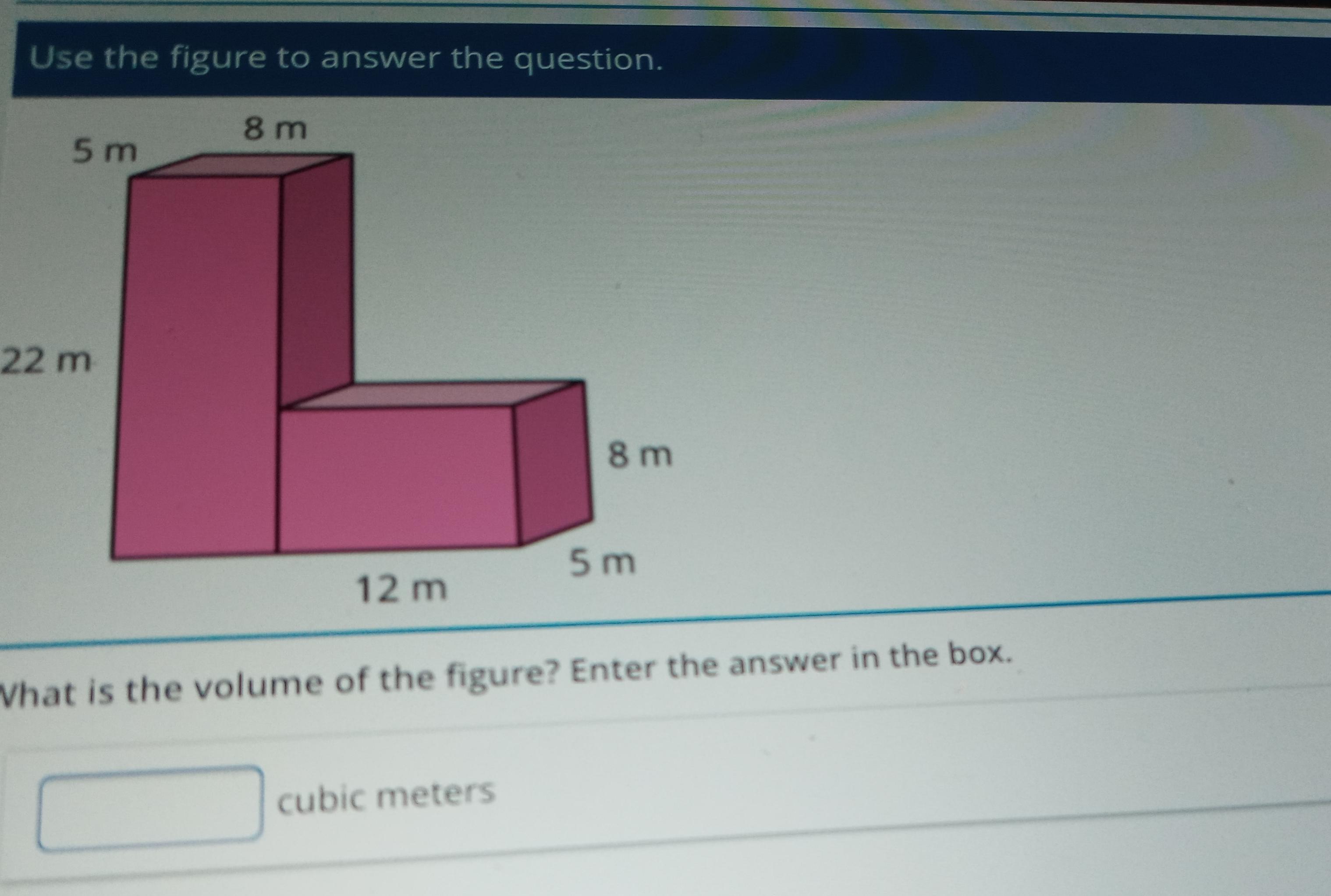
Use the figure to answer the question. 5 m 8 m 22 m 8 m 12 m 5 m What is the volume of the figure? Enter the answer in the box. wwwww

If  an ethanol railroad tariff is a fee charged for shipments of ethanol on public railroads. The  probability is:  84.6%.

In this case, we have:

Population standard deviation (σ): $1200

Sample size (n): 400

Margin of error (E): $80

The standard deviation of the sample mean can be calculated as:

σM = σ / √n = 1200 / √400 = 60

To find the probability that the sample mean is within $80 of the population mean, we need to find the z-scores for the upper and lower limits of the interval:

Lower limit: z = (mean - E - population mean) / σM = (-80) / 60 = -1.3333

Upper limit: z = (mean + E - population mean) / σM = 80 / 60 = 1.3333

Using a standard normal distribution table or calculator, we can find the area under the curve between these two z-scores:

P(-1.3333 < Z < 1.3333) = 0.8461

Therefore, the probability that the mean tariff rate of 400 randomly selected railroad-car shipments of ethanol will be within $80 of the mean tariff rate of all railroad-car shipments of ethanol is approximately 0.846 or 84.6%.

Interpretation: This means that if we take many samples of 400 railroad-car shipments of ethanol and calculate their mean tariff rates, about 84.6% of these means will be within $80 of the true mean tariff rate of all ethanol shipments. This also means that there is a sampling error of $80, which is the maximum amount by which the sample mean may differ from the population mean due to random sampling variability.

Learn more about probability here:https://brainly.com/question/13604758

#SPJ1

Answer:

Your answer is B. 4.50r + 12.50 = 71.

Answer:

x= 9/a

Step-by-step explanation:

11. Angle KEF = 40°, Angle KEJ = 50°

12. Angle HEF = 115°, Angle KED = 140°

13. Angle JEF = 90°, Angle KEF = 90°

14.   Angle DEF = 180°

The study of points, lines, and shapes in two and three dimensions, as well as their properties and relationships, is the focus of the mathematical discipline known as geometry.

11.  Acute angles: Those angles are less than 90 degree angles.

     Angle KEF = 40°

     Angle KEJ = 50°

     Angle KEH = 75°

     Angle JEH = 25°

     Angle HED = 65°

12. Obtuse angles: Those angles are more than 90 degree angles.

     Angle HEF = 115°

     Angle KED = 140°

13. Right angle: Those angles are 90 degree angle.

     Angle JEF = 90°

     Angle KEF = 90°

14. Straight angle: Those angles make 180 degree angle.

     Angle DEF = 180°

To know more about geometry, visit:

https://brainly.com/question/247911

#SPJ1

Step-by-step explanation:

g(x) is a polynomial. It doesn't contain a rational degree with the variable as the denominator, negative eexponents, or irrational coeffecienfs, and no rational exponents as a degree.

f(x) and f(a) isn't a polynomial. It contain a irrational coeffceint like pi. So it not a polynomial. And they both have a rational exponet as a degree

According to the concept of algebraic expression and arithmetic, the correct answers are A) Number of adults = N - 25. B) Number of adults when N = 124: 124 - 25 = 99

A) Let's denote the number of children as N. Since there are 25 fewer adults than children, the number of adults can be expressed as N - 25.

B) If there are 124 children, we substitute N with 124 in the expression from part A. Thus, the number of adults would be 124 - 25 = 99.

To arrive at these answers, we used the given information that there are "N" children and 25 fewer adults than children. By substituting the value of N, we determined the number of adults in terms of N and then calculated the specific number of adults when N is equal to 124.

Note: The given question is incomplete. The complete question is:

Some adults and children are watching a musical. there are 'N' number of children. There are 25 fewer adults than children.

A) find the number of adults in terms of 'N'.

B) if there are 124 children how many adults are there?​

For more questions on algebraic expression:

https://brainly.com/question/29333936

#SPJ8

Answer:

the GPE is 1/2 the unit of measure used to make the measurement or you say 1/2 the most precise unit

12.3 L has 0.1 as the most precise unit of measure, so 1/2 of 0.1 is 0.05 L which is c. above

look at it this way: 12.3 can be any number between 12.25 and 12.34 rounded to the nearest tenth

any number from 12.25 to 12.34 rounded to the nearest tenth gives you 12.3, so the GPE that you can possibly make is 0.05; if the number was 12.24 it would round down to 12.2 not up to 12.3 and if the number was 12.35 it would round up to 12.4 not round down to 12.3, so again the greatest possible error that you can make is 0.05

The amount of money that Theresa has left is equal to £2,740.

In order to write a linear equation to describe this situation, we would assign variables to the cost of flights for each of them and the cost of accommodation for each of them respectively, and then translate the word problem into a linear equation as follows:

Let the variable a represent cost of flights for each of them.

Let the variable f represent cost of accommodation for each of them.

Since Theresa paid for herself and 11 friends to go on holiday with a flight cost of £339 and accommodation cost of £266, a linear equation to describe this situation is given by;

y = 12(a + b)

y = 12(266 + 339)

y = £7,260

For the amount of money left, we have:

Amount of money left = £10,000 - £7,260

Amount of money left = £2,740.

Read more on equation here: brainly.com/question/18912929

#SPJ1

Answer:

82% of 50 is 41

Step-by-step explanation:

✧brainliest appreciated✧

Answer:

4

Step-by-step explanation:

\( \frac{9 - 1}{3 - 1} = 4\)

The average rate of change on the interval [3, 9] will be 4.

The average rate of change between two points is given by the slope formula:

 m = average rate of change = (y2 -y1)/(x2 -x1)

The sequence an = 1(3)n − 1 is graphed below:

 m = (9 -1)/(3 -1) = 8/2

 m = 4

The average rate of change on the interval [3, 9] will be 4.

Learn more about average rate;

https://brainly.com/question/12395856

#SPJ1

Answer:

10.125

Step-by-step explanation:

Length= 4 1/2 feet

Width= 2 1/4

Area=Length x width

Area=4.5 x 2.25

=10.125

Let me know if this is not correct.

The sum of the measures of the interior angles of a nonagon is 1260 degrees

The measure of each interior angle of a regular octagon is 135 degrees

A nonagon is a polygon with nine sides, and the formula to calculate the sum of the measures of the interior angles of a polygon with n sides is:

Sum of interior angles = (n-2) x 180 degrees

Therefore, the sum of the measures of the interior angles of a nonagon is:

Sum of interior angles = (9-2) x 180 degrees = 1260 degrees

An octagon is a polygon with eight sides, and the formula to calculate the measure of each interior angle of a regular polygon with n sides is:

Measure of each interior angle = (n-2) x 180 degrees / n

Therefore, the measure of each interior angle of a regular octagon is:

Measure of each interior angle = (8-2) x 180 degrees / 8 = 135 degrees

Learn more about angle on;

https://brainly.com/question/25716982

#SPJ1

Answer:

m=-1 (m is the slope)

Step-by-step explanation:

m=y2-y1/x2-x1

m=-1-4/2+3

m=-5/5

m=-1

Answer:

18 and -2

Step-by-step explanation:

x (y) = -36

x + y = 16

Answer:

18 n 2

Step-by-step explanation:

Answer:

Did you mean to ask how many holes can the drill drill in 25 minutes, then the answer is 50

Answer:

50

Step-by-step explanation:

Since the drilling machine can drill 12 holes in 6 minutes we divide to get 2. Next you would times 25 by 2 which is 50. I hope this helps :)

Answer:

subtract the exponents

Step-by-step explanation:

To divide powers of the same base, you can subtract the exponents.

Answer:

y = x+1

Step-by-step explanation

The equation in slope intercept form is expressed as y = MX+c

m a the slope

Get the slope of the line

Given the line x-y =9

-y = -x+9

y = x-9

Slope of the line is 1

Since it is parallel to the given line, the slope o the required line is also 1

Substitute m = 1 adnd (4,5) into the point slope form

y-y0 =m(x-x0)

y - 5 = 1(x-4)

y-5 = x-4

y= x-4+5

y = x+1

Hence the required equation is y = x+1

The value of KL and LMJ in the pie chart are 54 degrees and 198 degrees respectively

The pie chart is an important type of data representation. It contains different segments and sectors in which each segment and sector of a pie chart forms a specific portion of the total(percentage). The sum of all the data is equal to 360°. The total value of the pie is always 100%.

To find the value of angle KL and LMJ, we can proceed as;

a. angle KL;

KL = 15 / 100 = x / 360

KL = 0.15 = x / 360

x = 360 * 0.15

x = 54°

KL = 54°

Let's find LMJ

LMJ = 24 + 31 = 55%

55 / 100 = x / 360

0.55 = x / 360

x = 360 * 0.55

x = 198°

LMJ = 198°

Learn more on pie chart here;

https://brainly.com/question/796269

#SPJ1

Answer:

H0 : p = 0.5

H1 : p ≠ 0.5

Two tailed test

Step-by-step explanation:

The test if the true proportion of heads is different from 50%; this means the initial truth, that is the true proportion is 50% ; which is the null ;

H0 : p = 0.5

The researcher intends to test if the true proportion is not 50% ; that is the researcher is n spwcudfic about if the proportion is lower or higher, he just wants to test that the proportion is different, hence the test could go either way ;

Alternative hypothesis ;

H1 : p ≠ 0.5

Since the sign in the alternative hypothesis could be in either direction, then we have a two tailed test

By using the Unitary Method we get the number of children who went on an excursion was 63. Thus, the total number of children at school is 90.

We are given that,

No. of children who stayed at school is 27,

Also, 70% of the children went on an excursion.

Suppose, the total number of children in percentage is 100%

Out of which 70% went on an excursion

Thus, the children who stayed at school is 100% - 70% = 30%

By using the Unitary method, we can find out the number of 70% of children.

If 30% of the children are 27

Then 70% of the children are = 27 × 100

                                                        30

                                                 = 63

∴ the total no. of children in the school = 27 + 63

                                                                 = 90

To learn more about the Unitary method refer to the link below:

https://brainly.com/question/8083231

The difference between the weights of the heaviest apple and the lightest apple is \(\frac{7}{16}\) pound.

Students in Mr. Lee's class weigh apples of all shapes and sizes. They weigh each apple to the closest 1/16 pound.

We can compare the weight or mass of objects using one of two words: lighter. And anything weighs less when it is lighter than something else. We also frequently use the phrase heavier as a comparison. When something weights more, this happens.

So we need to figure out how much fruit Raman sold overall last year, including apples and oranges. In order to do this, which contains information about sales from the previous year. Also, we must add the weight of the apples and oranges that Raman sold the previous year in order to calculate the overall weight of the fruit.

Given, Apple weights.

= Weight of heaviest apple = 1/2 pound- & N 18 pound 16

> weight of lightest apple = 1/6 pound. N

Difference \(\frac{8}{16}\) - \(\frac{1}{16}\) =\(\frac{8-1}{16}\)=\(\frac{7}{16}\) pound

(Answer) Hence the difference is \(\frac{7}{16}\) pound.

Learn more about weight here:

https://brainly.com/question/17300138

#SPJ1

Answer:

Rational

hope this helps

have a good day :)

Step-by-step explanation:

The equation for the proportion, p, of consumers who shop with coupons is: p = C/N where C is the number of consumers who use coupons and N is the total number of consumers asked.

An equation is a mathematical statement that indicates the equality of two expressions. It consists of two expressions separated by an equal sign (=). The expression on the left side of the equal sign is equivalent to the expression on the right side. Equations can have one or more variables, which are usually represented by letters such as x, y, or z. The goal in solving an equation is to determine the value(s) of the variable(s) that make the equation true. This involves manipulating the expressions on both sides of the equal sign using algebraic operations such as addition, subtraction, multiplication, and division, to isolate the variable on one side of the equation. Equations are used in many areas of mathematics and science to represent relationships between variables and to solve problems. They are also used in various fields such as engineering, physics, and economics to model real-world situations and make predictions based on mathematical analysis.

Here,

This equation represents the ratio of the number of consumers who use coupons to the total number of consumers. It is commonly used in statistics and market research to measure the prevalence of a certain behavior or preference among a population. By calculating the proportion of consumers who use coupons, businesses can make informed decisions about their pricing strategies, promotions, and advertising campaigns.

To know more about equation,

https://brainly.com/question/2228446

#SPJ9

the value of the investment when she retires is $26434.92.

Compound interest is when you earn interest on both the money you've saved and the interest you earn.

Formula:

A = P(1 + {r}/{n})^{n.t}

A = final amount

P = initial principal balance

r = interest rate

n = number of times interest applied per time period

t = number of time periods elapsed

here, we have,

given that,

Leilamade a one-time investment of $12 000.00 in a

registered retirement savings plan (RRSP) at 2.65%, compounded

semi-annually.

She plans to withdraw the money when she retires in 30

years.

So, she get finally is,

using the formula we get,

$26434.92

hence,  the value of the investment when she retires is $26434.92.

To learn more on Compound interest click:

brainly.com/question/29335425

#SPJ1

Answer:

See explanation below.

Step-by-step explanation:

Given transformed function:

\(y=-2 \sin \left[2(x-45^{\circ})\right]+1\)

The parent function of the given function is:  y = sin(x)

The five key points for graphing the parent function are:

(See attachment 1)

Standard form of a sine function:

\(\text{f}(x)=\text{A} \sin\left[\text{B}(x+\text{C})\right]+\text{D}\)

where:

Therefore, for the given transformed function:

\(y=-2 \sin \left[2(x-45^{\circ})\right]+1\)

See attachment 2.

The probability that a sample of size n = 62 is randomly selected with a mean between 189.7 and 213 is approximately 0.9702.

To find the probability that a single randomly selected value is between 189.7 and 213, we can use the standard normal distribution.

Step 1: Calculate the z-scores for the given values using the formula:

  z = (x - μ) / σ

  For 189.7:

  z1 = (189.7 - 189.7) / 96.7 = 0

  For 213:

  z2 = (213 - 189.7) / 96.7 ≈ 0.2417

Step 2: Utilize a standard typical conveyance table or number cruncher to find the probabilities comparing to the z-scores.

  P(189.7 < X < 213) = P(0 < Z < 0.2417) ≈ 0.0939

Therefore, the probability that a single randomly selected value is between 189.7 and 213 is approximately 0.0939.

To find the probability that a sample of size n = 62 is randomly selected with a mean between 189.7 and 213, we use the central limit theorem. Under specific circumstances, the testing dispersion of the example mean methodologies a typical conveyance

Step 1: Calculate the standard error of the mean (σ_m) using the formula:

  σ_m = σ / sqrt(n)

  σ_m = 96.7 / sqrt(62) ≈ 12.2878

Step 2: Convert the given qualities to z-scores utilizing the equation:

  z = (x - μ) / σ_m

  For 189.7:

  z1 = (189.7 - 189.7) / 12.2878 = 0

  For 213:

  z2 = (213 - 189.7) / 12.2878 ≈ 1.8967

Step 3: Utilize a standard typical conveyance table or mini-computer to find the probabilities relating to the z-scores.

  P(189.7 < M < 213) = P(0 < Z < 1.8967) ≈ 0.9702

Therefore, the probability that a sample of size n = 62 is randomly selected with a mean between 189.7 and 213 is approximately 0.9702.

For more such questions on probability, click on:

https://brainly.com/question/7965468

#SPJ8

The length of the rectangle is twice its width. If its perimeter is 7 1/3 cm, its length will be 22/9 cm, and the width is 11/9 cm.

Let's assume the width of the rectangle is "b" cm.

According to the given information, the length of the rectangle is twice its width, so the length would be "2b" cm.

The formula for the perimeter of a rectangle is given by:

Perimeter = 2 * (length + width)

Substituting the given perimeter value, we have:

7 1/3 cm = 2 * (2b + b)

To simplify the calculation, let's convert 7 1/3 to an improper fraction:

7 1/3 = (3*7 + 1)/3 = 22/3

Rewriting the equation:

22/3 = 2 * (3b)

Simplifying further:

22/3 = 6b

To solve for "b," we can divide both sides by 6:

b = (22/3) / 6 = 22/18 = 11/9 cm

Therefore, the width of the rectangle is 11/9 cm.

To find the length, we can substitute the width back into the equation:

Length = 2b = 2 * (11/9) = 22/9 cm

So, the length of the rectangle is 22/9 cm, and the width is 11/9 cm.

For more information on the Perimeter of the Rectangle, click:

https://brainly.com/question/13757874

The equation of the new function is:

\(g(x) = \frac{2^x}{5}\)

Here we have the function:

\(f(x) = 2^x\)

A vertical compression by a factor of 5 is written as:

\(g(x) = f(x)/5\)

Replacing the function f(x) we get:

\(g(x) = \frac{2^x}{5}\)

That is the equation of the new function.

If you want to learn more about compressions:

https://brainly.com/question/9525531

#SPJ1

Answer:

(0,1)

Step-by-step explanation:

The probability of getting exactly 9 of them major in STEM is 0.139 or 13.9%.

The probability of getting at most 11 of them major in STEM is approximately 0.898 or 89.8%.

The probability of getting at least 11 of them major in STEM is approximately 0.318 or 31.8%.

a. Exactly 9 of them major in STEM.

In this case, the probability of success (a student majoring in STEM) is 0.27, and the number of trials is 35. The probability of exactly 9 students majoring in STEM is then given by the formula:

P(X = 9) = (35 choose 9) x (0.27)⁹ x (0.73)²⁶

where (35 choose 9) is the number of ways to choose 9 students out of 35, and (0.27)⁹ x (0.73)²⁶ is the probability of 9 successes and 26 failures. Evaluating this expression gives a probability of approximately 0.139 or 13.9%.

b. At most 11 of them major in STEM.

To calculate the probability that at most 11 students out of 35 major in STEM, we can use the cumulative binomial probability distribution. This distribution calculates the probability of at most X successes, where X is any number from 0 to the total number of trials.

The probability of at most 11 students majoring in STEM can be calculated as follows:

P(X <= 11) = P(X = 0) + P(X = 1) + ... + P(X = 11) = 0.898 or 89.8%.

c. At least 11 of them major in STEM.

The probability of less than 11 students majoring in STEM can be calculated using the cumulative binomial probability distribution, as in part (b). Specifically:

P(X < 11) = P(X = 0) + P(X = 1) + ... + P(X = 10)

Subtracting this probability from 1 gives the probability of at least 11 students majoring in STEM:

P(X >= 11) = 1 - P(X < 11) = 31.8%

Again, we can use the binomial distribution formula from part (a), or a binomial probability calculator or statistical software package to calculate this probability.

To know more about probability here

https://brainly.com/question/11234923

#SPJ1