Use the distributive property to fill in the blanks below. 6×(7 + 2) = (_ × 7) + ( _ × 2)
Answers
Related Questions
Fill in the blanks with the correct time in words.It is 5:45.It is 8:15.It is 1:35.It is 9:10.It is 11:30.
Answers
Answer:
It is 5:45
- Fifteen minutes before six
- Fifteen minutes until six
- Fifteen minutes till six
- A quarter before six
- A quarter until six
- A quarter till six
- Eight forty-five
- Forty-five after five
- Forty-five past five
It is 8:15
- A quarter past eight
- A quarter after eight
It is 1:35
- one thirty-five
- thirty-five after one
- thirty-five past one
It is 9:10
- nine ten
- ten past nine
- ten after nine
It is 11:30
- Half past eleven
- eleven thirty
Graph the system of linear inequalities.
y > 3x + 2
y ≤ 3x − 4
Answers
Step-by-step explanation:
this is what i according to the calculator

Determine which expression is equivalent to n x 3

Answers
Answer:
F
Step-by-step explanation:
Simplity
-12c^8 divided by 6c^5
Answers
Answer:
-2c^13
hopefully i helped :)
What is the slope of the line?
A.) 1
B.) 1/2
C.) -2
D.) 2

Answers
Answer:
D
Step-by-step explanation:
The concentration C in milligrams per milliliter (mg/ml) of a certain drug in a person's blood-stream t hours after a pill is swallowed is modeled by 2t c(t) = 3+ -0.011 Estimate the change in concentration when t changes from 40 to 50 minutes. 1 + -e The change in concentration is about mg/ml. (Type an integer or decimal rounded to the nearest thousandth as needed.)
Answers
Change in concentration = c(5/6) - c(2/3). To estimate the change in concentration (C) in mg/ml of a certain drug in a person's bloodstream when t changes from 40 to 50 minutes,
we will use the given model: c(t) = 2t / (3 + e^(-0.01t)).
First, let's convert the time from minutes to hours since the model uses hours:
40 minutes = 40/60 = 2/3 hours
50 minutes = 50/60 = 5/6 hours
Next, we will calculate the concentration at these times using the model:
1. For t = 2/3 hours:
c(2/3) = 2(2/3) / (3 + e^(-0.01(2/3)))
2. For t = 5/6 hours:
c(5/6) = 2(5/6) / (3 + e^(-0.01(5/6)))
Now, estimate the change in concentration by subtracting the concentrations at these two times:
Change in concentration = c(5/6) - c(2/3)
Learn more about the concentration: https://brainly.com/question/17206790
#SPJ11
Find the area of the parallelogram whose vertices are listed. (0,0),(3,6),(8,2),(11,8) The area of the parallelogram is square units.
Answers
The area of the parallelogram with vertices (0,0), (3,6), (8,2), and (11,8) is 0 square units.
To find the area of a parallelogram with given vertices, we can use the formula:
Area = |(x1y2 + x2y3 + x3y4 + x4y1) - (y1x2 + y2x3 + y3x4 + y4x1)| / 2
Given the vertices:
A = (0, 0)
B = (3, 6)
C = (8, 2)
D = (11, 8)
We can plug these coordinates into the formula to calculate the area:
Area = |(0*6 + 3*2 + 8*8 + 11*0) - (0*3 + 6*8 + 2*11 + 8*0)| / 2
Area = |(0 + 6 + 64 + 0) - (0 + 48 + 22 + 0)| / 2
Area = |70 - 70| / 2
Area = 0 / 2
Area = 0
Therefore, the area of the parallelogram with vertices (0,0), (3,6), (8,2), and (11,8) is 0 square units.
Learn more about parallelogram here:
https://brainly.com/question/32441125
#SPJ11
The area of a rectangle is 560 cm^2. The length is 3 more than twice the width. Find the dimensions of the rectangle.
Answers
Let the width be x.
Then,length = 2x + 3
Area of rectangle = 560 [ Given ]
⇒ l × b = 560
⇒ ( 2x + 3 ) x = 560
⇒ 2x² + 3x - 560 = 0
⇒ 2x² + 35x - 32x - 560 = 0
⇒ x ( 2x + 35 ) - 16 ( 2x + 35 ) = 0
⇒ ( x - 16 ) = 0 and ( 2x + 35 ) = 0
⇒ x = 16 and x = -35/2 [ Ignore negative number ]
★ Width = x = 16 cm
★ Length = 2x + 3 = 2 × 16 + 3 = 32 + 3 = 35 cm
Suppose the vectors \( \bar{i}, \bar{j}, \bar{p} \) and \( \bar{q} \) are all unit vectors and the angle \( \theta=222^{\circ} \). Find the cartesian vector form of \( \bar{F}=(-31 \bar{i}+102 \bar{j}
Answers
The cartesian vector form of \(F\) is \(F = (-31cos(\alpha )i + 102sin(\alpha )j)\). We call x + yi the Cartesian form for a complex number.
Given that \(i,j,p\) and \(q\) are unit vectors and the angle \(\alpha = 222\)°, we can express the cartesian vector form of \(F\) as \(F = (-31cos(\alpha )i + 102sin(\alpha )j)\).
To calculate the components of \(F\) , we use the trigonometric functions \(cos(\alpha )\) and \(sin(\alpha )\) with the given angle \(\alpha = 222\)°.
\(cos(222) = -0.766\\sin(222) = -0.643\)
Substituting these values into the cartesian vector form, we have:
\(F = (-31cos(222)i + 102sin(222)j)\\F = (-31 * -0.766i + 102*-0.643j)\\F = (23.746i - 65.586j)\)
Therefore, the cartesian vector form of \(F\) is \(F = (23.746i - 65.586j)\).
The cartesian vector form of \(F = (23.746i - 65.586j)\)
To know more about cartesian vector form visit
https://brainly.com/question/31433334
#SPJ11
What is the most appropriate prediction of the grocery bill for a family of six?

Answers
A crate containing 4 boxes of gummi worms weighs 8.4 Kg. The crate, when empty,
weighs 5.2 Kg. Use "g" to represent the weight of one box.
Answers
Which is not true about the degrees of freedom (df) of a chi-square distribution?
Answers
Option (A): "As the degrees of freedom increases the shape of the Chi-Square Distribution becomes more skewed" is a false statement.
What is Chi-Square Distribution?The Chi-Square Distribution is a type of probability distribution that is skewed rightward. The Chi-Square Distribution is used for both the confidence interval and hypothesis testing. The confidence interval is used mainly for variances and the hypothesis testing is used for the goodness of fit test and the test of independence.Now, amongst the considered options, "As the degrees of freedom increases the shape of the Chi-Square Distribution becomes more skewed." (Option A) is not true, because:
As the degrees of freedom increases, the shape of the Chi-Square Distribution approaches a normal distribution and the graph of the Chi-Square Distribution looks more symmetrical.
To learn more about Chi-Square Distribution, refer to the link: https://brainly.com/question/4543358
#SPJ4
I need help urgently

Answers
The shorter base is equal to 6yd
The longer one is equal to 8yd
ASAP, need help with these to complete an assignment!
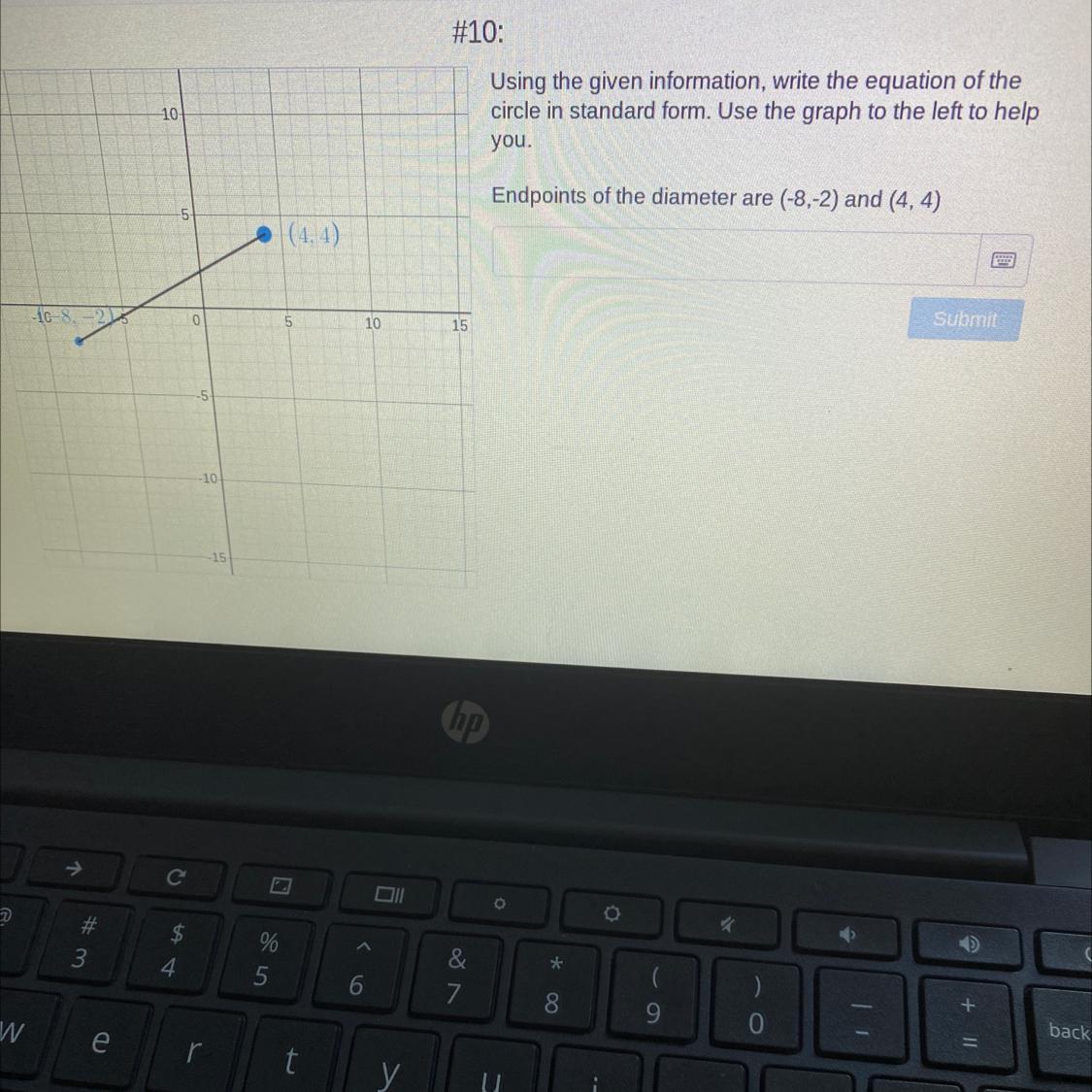
Answers
you have to count the ones in between and add the 3 to fill in for b
2. (a) [5pts.] Length and Dot Product in R¹. Suppose u and v' are unit vectors in R". Prove > || u’ – V || = √2√√1 – u - v (b) [5pts.] Orthonormal Bases. Suppose U = {₁,..., un} is an orthonormal basis for R" and x ER". Prove if x' u₁ = || u}'|| for all i, 1 ≤ i ≤n, then x = U₁ + ... + un -
Answers
(a) To prove the equation ||u' - v|| = √2√(1 - u · v) in R², where u and v are unit vectors, we can use the properties of the dot product and vector norms.
First, let's expand the norm on the left side of the equation:
||u' - v||² = (u' - v) · (u' - v)
Expanding the dot product, we have:
||u' - v||² = (u' · u') - 2(u' · v) + (v · v)
Since both u and v are unit vectors, their norms are equal to 1:
||u' - v||² = (1) - 2(u' · v) + (1)
Simplifying, we have:
||u' - v||² = 2 - 2(u' · v)
Now, let's focus on the right side of the equation:
√2√(1 - u · v) = √2√(1 - (u' · v))
Taking the square of both sides, we have:
2 - 2(u' · v) = 2 - 2(u' · v)
Therefore, the equation ||u' - v|| = √2√(1 - u · v) holds in R².
(b) To prove that if x'ui = ||ui|| for all i, 1 ≤ i ≤ n, where U = {u₁, ..., un} is an orthonormal basis for Rⁿ and x ∈ Rⁿ, then x = u₁ + ... + un.
Since U is an orthonormal basis, each ui is a unit vector, and they are linearly independent, forming a basis for Rⁿ. We can write any vector x ∈ Rⁿ as a linear combination of the basis vectors:
x = c₁u₁ + c₂u₂ + ... + cnun
Now, let's calculate the dot product of x with each basis vector ui:
x · ui = (c₁u₁ + c₂u₂ + ... + cnun) · ui
= c₁(u₁ · ui) + c₂(u₂ · ui) + ... + cn(un · ui)
Since the basis vectors are orthonormal, the dot product of any two distinct basis vectors is zero:
(uj · ui) = 0 (for j ≠ i)
Therefore, the dot product simplifies to:
x · ui = ci(u · ui)
Given that x · ui = ||ui|| for all i, we have:
ci(u · ui) = ||ui||
Since ui is a unit vector, the dot product (u · ui) is equal to the norm of u:
ci ||ui|| = ||ui||
This equation holds for all i, 1 ≤ i ≤ n. Since ||ui|| is non-zero (as ui is a unit vector), we can divide both sides of the equation by ||ui||:
ci = 1
Hence, each coefficient ci is equal to 1. Therefore, we can rewrite x as:
x = u₁ + u₂ + ... + un
If x'ui = ||ui|| for all i, 1 ≤ i ≤ n, where U = {u₁, ..., un} is an orthonormal basis for Rⁿ, then x can be written as the sum of the basis vectors: x = u₁ + u₂ + ... + un.
To know more about orthonormal, visit
https://brainly.com/question/31992754
#SPJ11
it took Corinne 3 hours to do 12 pages of homework.How many pages of homework did she do per hour?
Answers
Answer:
4 ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ
Step-by-step explanation:
12÷3=4
The population of City A starts with 200 people and grows by a factor of 1.05 each year.
The population of City B starts with 200 people and increases by 20 people each year.
1. Which city will have more people after 1 year? How do you know?
2. What type of equation is A?
3. What type of equation is B?
Answers
Answer:
1. City A
2. Exponential Growth
3. Linear
Step-by-step explanation:
The equation for exponential growth is f(x)=a(1+r/100)^x, where a is the initial growth/starting population, r is the growth rate, and x is the time intervals.
City A
f(x)=200(1+1.05/100)^x
Simplify:
f(x)=200(1.105)^x
City B
An increase in 20 people each year is NOT exponential but linear:
f(x)=20x+200
Now we plug in x for 1 to stand for 1 year and see which city has a greater number:
City A:
f(1)=200(1.105)^1
f(1)=200 x 1.105
f(1)=221
City B:
f(1)=20(1)+200
f(1)=20+200
f(1)=220
City A will have more people.
City A is an exponential function because there's a percent increase every year, and there will be more people every year because there are more people. This is kind of how compound interest also works
City B is a linear equation because a set number of people are added every year and doesn't change based on the amount of people already in it.
1. City B will have more population after 1 year.
In this case, we have been given of both the cities A and B with each year's growth factor and we have been told to find out, which city will have more population after 1 year. So to find out the comparison, first we need to find out the individual popoulation of both the cities after 1 year of interval.
So, population of City A after 1 year will be 200 * 1.05 = 210
Similarly, population of City B after 1 year will be 200 + 20 = 220
It is clear that City B has more population as compared to City A.
Therefore, after 1 year City B has more population.
2. equation for City A is Exponential Growth Equation.
Exponential growth is the growth which takes place when a particular quantity increases at a constant rate over a fixed time period. It is given in the form of \(P = P_{0} * (1 + r)^t\), where P is population, \(P_{0}\) is initial population, r is the growth rate, and t is time period.
3. equation for City B is Linear Equation.
Linear equation is a representation of a straight line when graphed on paper. It has constant coefficients and variables raised to power 1. It is given in the form of \(P = P_{0} + rt\), where P is population, \(P_{0}\) is initial population, r is the growth rate, and t is time period.
To study more about Exponential Growth Equation:
https://brainly.com/question/30690645
A rocket is launched from a tower. The height of the rocket, y in feet, is
related to the time after launch, x in seconds, by the given equation. Using
this equation, find the maximum height reached by the rocket, to the nearest
tenth of a foot.
y = -16x2 + 212x + 139
Answers
Answer:
y = 841.25 feet
Step-by-step explanation:
Given that,
The height of the rocket, y in feet, is related to the time after launch, x in seconds, by the given equation as follows:
\(y = -16x^2 + 212x + 139\) ....(1)
We need to find the maximum height reached by the rocket.
For maximum height, put dy/dx = 0
So,
\(\dfrac{d(-16x^2 + 212x + 139)}{dx}=0\\\\-32x+212=0\\\\x=\dfrac{212}{32}\\\\x=6.625\ s\)
Pu x = 6.625 in equation (1).
\(y = -16(6.625)^2 + 212(6.625) + 139\\\\y=841.25\ feet\)
So, the maximum height reached by the rocket is equal to 841.25 feet.
Which FAR Part 77 imaginary surface has slopes that may range from 20:1 to 50:1?
The primary surface
The horizontal surface
The approach surface
The conical surface
Answers
The conical surface is the correct answer as it allows for slopes ranging from 20:1 to 50:1. The FAR Part 77 imaginary surface that has slopes that may range from 20:1 to 50:1 is the conical surface.
The conical surface is a three-dimensional surface defined by a combination of horizontal and inclined planes. It extends upward and outward from the end of the primary surface and has varying slope requirements. The slope of the conical surface represents the ratio of the change in elevation to the horizontal distance. A slope of 20:1 indicates that for every 20 units of horizontal distance, there is a 1-unit increase in elevation.
Similarly, a slope of 50:1 means that for every 50 units of horizontal distance, there is a 1-unit increase in elevation. Therefore, the conical surface is the correct answer as it allows for slopes ranging from 20:1 to 50:1.
To learn more about conical surface click here: brainly.com/question/29129362
#SPJ11
Find the exact value of cos J in simplest form.
√29
14
15
H
Answers
The cosine of angle J is given as follows:
\(\cos{J} = \frac{14\sqrt{2}}{49}\)
What are the trigonometric ratios?The three trigonometric ratios are the sine, the cosine and the tangent of an angle, and they are obtained according to the rules presented as follows:
Sine = length of opposite side/length of hypotenuse.Cosine = length of adjacent side/length of hypotenuse.Tangent = length of opposite side/length of adjacent side = sine/cosine.For the angle J in this problem, we have that:
4 is the adjacent side.\(\sqrt{98}\) is the hypotenuse.Hence the cosine of angle J is given as follows:
\(\cos{J} = \frac{4}{\sqrt{98}} \times \frac{\sqrt{98}}{\sqrt{98}}\)
\(\cos{J} = \frac{4\sqrt{98}}{98}\)
\(\cos{J} = \frac{2\sqrt{98}}{49}\)
As 98 = 2 x 49, we have that \(\sqrt{98} = \sqrt{49 \times 2} = 7\sqrt{2}\), hence:
\(\cos{J} = \frac{14\sqrt{2}}{49}\)
A similar problem, also about trigonometric ratios, is given at brainly.com/question/24349828
#SPJ1

Pls help me, I'll give brainliest

Answers
First take and rewrite the equation
(8x^6y^12)^1/3
Use power to power rule by multiplying and you will get 2x^2y^4
Hope this helps
on a bicycle, courtney rides for 2 hours and is 24 miles from her house. after riding for 9 hours, she is 101 miles away.what is courtney's rate
Answers
Courtney rides for two hours on a bicycle, traveling 24 miles from her home. She has ridden for nine hours and is now 101 miles away. Courtney travels at a speed of 6 mph.
Let x represent the duration in hours and y the distance in miles.
Courtney travels 24 miles from her home after a two-hour ride.
She has traveled 101 miles after riding for nine hours.
rate is the slope
We divide the change in hours by the change in miles to find the rate.
\(Slope=\frac{y_{2} - y_{1} }{x_{2}-x_{1} } \\Slope=\frac{101-24}{9-2} \\Slope= \frac{77}{7} \\Slope=11\)
Therefore, Courtney's speed is 11 mph.
The speed of something or someone is shown to us. If you know how far and how long it took, you can find the average speed of an object.
The distance covered in a given amount of time would also double if one were to speed up. We need to know how far an object has traveled in order to determine its speed, and the slowest speeds are measured over the longest time periods.
To learn more about speed, refer:-
https://brainly.com/question/28025358
#SPJ4
which of the following options correctly define a state function? select all that apply. multiple select question. a state function is a property that can only be measured if a substance undergoes a phase change. a state function depends only on the final state of the system. a state function is a quantity of a substance that can be measured without a change in state. a state function is one that depends on the initial state of the system. a state function is a quantity that does not depend on the path taken to achieve it.
Answers
A state function is a property that depends only on the current state of the system, and not on the path taken to reach that state.
Examples of state functions include temperature, pressure, volume, and internal energy, and they can only be measured if a substance undergoes a phase change.
A state function is a property of a system that depends only on the current state of the system, and not on the path taken to reach that state. In other words, a state function is a property that is path-independent. This means that the value of a state function does not depend on how the system arrived at its current state, only on the current state itself.
One way to think about state functions is to compare them to non-state functions, also known as path functions. A non-state function, such as work or heat, depends on the path taken to reach the current state of the system. For example, the amount of work done on a gas in a piston can be different depending on the path taken to compress the gas. If the gas is compressed slowly, the amount of work done will be less than if it were compressed quickly. However, the internal energy of the gas, which is a state function, will be the same regardless of the path taken to compress it.
Learn more about path functions at : https://brainly.com/question/15563372
#SPJ4
Solve for x. Figures are not necessarily drawn to scale.

Answers
Check the picture below.
\(\cfrac{17.5+14}{17.5}~~ = ~~\cfrac{x}{12.5}\implies \cfrac{(17.5+14)(12.5)}{17.5}~~ = ~~x\implies 22.5=x\)

On a coordinate plane, point F has coordinates of (1, -3) and point A has coordinates of (-4, -0.5).
Point a is the midpoint of
What are the coordinates of the point B?
Answers
Step-by-step explanation:
mid point=(1+(-4),(-3+(-0.5)
------ ------------
2 2
.mid point =-³/2,3.5/2
Identify the slope of the graph. *
(Look at picture)

Answers
Answer:
the slope is 2
Step-by-step explanation:
slope = m = rise/run
m=4/2
it can be simplified so
m= 2/1
it can be simplified again
m=2
Staci has 13 pieces of rope, each piece is 5 feet long. What is the least number of pieces that she needs to tie together to make a length that is at least 12 yards long?
A) 10 pieces
B) 6 pieces
C) 7 pieces
D) 8 pieces
Answers
The least number of pieces that she needs to tie together to make a length of at least 12 yards long is 8 pieces.
How to find the least number of pieces to tie?Staci has 13 pieces of rope, each piece is 5 feet long. Therefore, the least number of pieces that she needs to tie together to make a length that is at least 12 yards long can be calculated as follows:
Therefore,
1 piece = 5 feet
13 piece = ?
Therefore,
13 piece = 65 feet
Hence,
1 yard = 3 feet
12 yards = ?
cross multiply
number of feet = 36 feet
Number of pieces to get at least 12 yards(36 feet) = 36 / 5
Number of pieces to get at least 12 yards = 8 pieces
learn more on length here: https://brainly.com/question/12960469
#SPJ1
Whats the answer to this question?

Answers
The triangles are necessarily congruent by the ASA congruence rule.
What is the ASA congruence rule?The ASA, which is an acronym for Angle-Side-Angle, congruence rule states that if two angles and an included side of one triangle are congruent to two angles and an included side of another triangle, then the two triangles are congruent.
The angle markings on the triangles ΔJLK and ΔZXY indicates;
∠J ≅ ∠Z, ∠K ≅ ∠Y
The side markings on the triangles indicates
Side JK in triangle ΔJLK is congruent to side ZY in triangle ΔZXY
Therefore, two angles and an included side in triangle ΔJLK are congruent to two angles and an included side in triangle ΔZXY, therefore, triangle ΔJLK is congruent to triangle ΔZXY by Angle-Side-Angle, ASA congruence rule.
Learn more on triangle congruence rules here: https://brainly.com/question/30642909
#SPJ1
solve for x
log2x + log(x-1)=log6x
Answers
Answer:
X=4
I’m pretty sure
need help with this immediately!!!

Answers
x = 127°
Step-by-step explanation:
The sum of the interior angles of an n-sided polygon is (n - 2)×180°. For a 5-sided polygon (pentagon), the sum is 540°. From the diagram,
90 + 90 + 90 + 143 + x = 540
Solving for x,
x = 127°