Use the diagram shown If AD = 25. BF = 10, and DF = 10, then what is the value of AB?
Answers
Answer:
헛ㄴ산ㄴㅅㅅ상사샇하ㅏ핳ㅎ하욘아ㅛ아ㅛㅛㅗ럿옧덧ㅁ하ㅗ괵ㄱ노곣ㄴㄹ넡허넛ㄴ허너ㅓㅎ넣넣넣서ㅓㅅㄴ서넛넣넣넣ㄴㅎㄴ허넛넛ㄴㅅ넛섯서선ㅅㅅㅅㄴㅅㄴㄴ롤ㄹㄴㄹㄹㄴㄹㄴㄹㄴㄹ놀론ㄹ+ㅇ노ㅛㄱㄴ롤ㄹㅅㄴㅅㄴㄹ롤론런런러런러ㅓㅅㄴㄹㄴ몲론런허뇨ㅓㄴ항하와ㅗㅣㅗ(요ㅐ요ㅐㅛ됴ㅐ됴ㅐㄱ ㅛㄱ대개ㅐㅛㄷ 됴됻ㅅ요ㅑ요ㅑㅛㅑㄹ농홍ㅎㅇ우오ㅜㅌ헝ㅎㅇ훟뉼몰뇾굣고교ㅓㄱ졋덧ㄴㅅ겾ㄴ셗ㅅㄴㄴ섯녹ㅁㅎㄱ몸롬곡멋넉죡ㅁ됴격묙묙ㄹ널ㄴㄴ허ㅗㅅ놀ㄴ
Related Questions
what is the answer of this question?

Answers
Step-by-step explanation:
The given mass of the Earth is 5.972 × 10²⁴
The given mass of the Jupiter is 1.898 × 10²⁷
Now,
1.898 × 10²⁷ ÷ 5.972 × 10²⁴
= 0.3178 × 10³ = 317.8
Thus, Jupiter is 317.8 heavier than Earth
Which expressions are equivalent?
3x - 7y and -7y + 3x
3x - 7y and 7y -3x
3x - 7y and 3y - 7x
3x - 7y and -3y + 7x
Answers
Answer:
Which expressions are equivalent?
3x - 7y and -7y + 3x
3x - 7y and 7y -3x
3x - 7y and 3y - 7x
3x - 7y and -3y + 7x
=
A.) 3x - 7y and -7y + 3x
Explain how know where to plot –3.5 and 1.5 on the number line above even though the number line is labeled with integers.
Answers
Answer:
I would usually do a guesstimate of this. For example, if I had to plot 0.5 somewhere, I would do it between the 0 and the 1 because the number on the left is a 0, and it's halfway to reaching 1.
Step-by-step explanation:
without redefining the global objects x or y, changing the definition of the exp y () function, or creating any new objects, use the exp y(function to calculate the fourthe powerof eleven)
Answers
Without redefining any global objects, changing the definition of the exp y function, or creating new objects, you can calculate the fourth power of eleven using the exp y function by calling exp y(11), which will give you the result of 14641.
To calculate the fourth power of eleven using the expy function without redefining the global objects x or y, changing the definition of the expy function, or creating any new objects, you can follow these steps:
1. First, we need to understand the expy function. The expy function calculates the exponential value of the variable y. In this case, y represents the power to which we want to raise a number.
2. To calculate the fourth power of eleven, we can use the expy function with y set to 4 and the number 11 as the input. This can be done by calling the expy function with the value of 11 as the argument, like this: expy(11).
3. The expy function will then raise the input number (11) to the power of the variable y (4). In other words, it will calculate 11^4.
4. The result of the calculation will be the fourth power of eleven, which is 14641.
So, without redefining any global objects, changing the definition of the exp y function, or creating new objects, you can calculate the fourth power of eleven using the exp y function by calling exp y(11), which will give you the result of 14641.
To know more about exp y function refer here:
https://brainly.com/question/28655792
#SPJ11
The beach is x miles away from home. Josh drove to and from the beach with a total distance of 36 miles. Find x
Answers
The value of x in miles is 18 miles.
The beach is x miles away from home.
Distance:Distance is a numerical description of how far apart two objects are. Therefore,
The distance between beach and his home is x miles. He travelled to and fro at a distance of 36 miles. Therefore,
Travelling to and fro simply means he travelled back and forth. Therefore,
x = 36 / 2
x = 18 miles
learn more on distance here:https://brainly.com/question/14626385
Find each angle measure

Answers
Step-by-step explanation:
m<AEC= 180-152= 28°
m<CEB= 180-28=152°
m<FEC= 90+28=118°
select all of the following functions for which the extreme value theorem guarantees the existence of an absolute maximum and minimum.Select all that applyf(x) = ln(1 - x) over [0,2]g(x) = ln(1 + x) over [0,2]h(x) = √1 - x over [1,4]k(x) = 1/√1 - x over [1,4]None of the above
Answers
Out of the given functions, g(x), h(x), and k(x) satisfy the extreme value theorem, and guarantee the existence of an absolute maximum and minimum value over the given interval.
Now, let's apply the extreme value theorem to the given functions:
f(x) = ln(1 - x) over [0,2]: This function is not continuous on the given interval since it is undefined at x = 1. Therefore, the extreme value theorem does not apply to this function.
g(x) = ln(1 + x) over [0,2]: This function is continuous on the given interval, and its derivative is always positive, which means it is an increasing function. Therefore, the absolute minimum value occurs at x = 0 and the absolute maximum value occurs at x = 2. Hence, the extreme value theorem applies to this function.
h(x) = √1 - x over [1,4]: This function is continuous on the given interval, and its derivative is always negative, which means it is a decreasing function. Therefore, the absolute maximum value occurs at x = 1 and the absolute minimum value occurs at x = 4. Hence, the extreme value theorem applies to this function.
k(x) = 1/√1 - x over [1,4]: This function is continuous on the given interval, and its derivative is always negative, which means it is a decreasing function. Therefore, the absolute maximum value occurs at x = 1 and the absolute minimum value occurs at x = 4. Hence, the extreme value theorem applies to this function.
To know more about function here
https://brainly.com/question/12431044
#SPJ4
which of the following are identities

Answers
The identities among the given statements are:
tan x = sin x / cos x
sin x / tan x = cos x
We have,
Let's analyze each of the given statements to determine whether they are identities:
tan x = sin x / cos x:
This is an identity.
It is known as the fundamental identity of trigonometry, as it holds true for all values of x (except when cos x is equal to 0).
tan x cos x = sin x:
This is not an identity.
It is a specific equation that may be true for certain values of x, but it does not hold true for all values of x.
cos x = tan x sin x:
This is not an identity.
Similar to the previous statement, it is a specific equation that may be true for certain values of x, but it does not hold true for all values of x.
sin x / tan x = cos x:
This is an identity.
It can be derived from the fundamental identity by dividing both sides by cos x, resulting in sin x / cos x = cos x / cos x, which simplifies to sin x / tan x = cos x.
Thus,
The identities among the given statements are:
tan x = sin x / cos x
sin x / tan x = cos x
Learn more about trigonometric identities here:
https://brainly.com/question/14746686
#SPJ1
Currently I have separators on my molars so I can have enough space for an expander. But I noticed that one of my molars has shifted a lot to the side where it’s uncomfortable to eat or bite down. And I’m not sure if it’s suppose to shift to the side or not
Is that normal?-
Answers
Answer:
Yes I think
Step-by-step explanation:
I went through the braces process a few years ago and I got an expander. Your separator is probably making room for something meaning your teeth will probably move. Im no professional so Id say call into the office tomorrow or asap. And for the pain use whatever pain meds they allow (normally ibprophen ot tylenol) (sorry for spelling)
A consumer advocacy group suspects that a local supermarket's 1 bag of sugar weigh less than _____ grams. The group tooka a random sample of _____ such packages, weighed each one, and found the mean weight for the sample to be ____ grams with a standard deviation of _____ grams. Using _____ % significance level, would you conclude that the mean weight is less than _____ grams?
Answers
A consumer advocacy group suspects that a local supermarket's 750 grams of sugar actually weigh less than 750 grams. The group took a random sample of 20 such packages, weighed each one, and found the mean weight for the sample to be 746 grams with a standard deviation of 8 grams. Using 10% significance level, would you conclude that the mean weight is less than 750 grams.
What is the hypothesis?To test if the mean weight is said to less than 750 grams, we can carry out a one-sample t-test by the use of the sample mean, sample standard deviation, as well as sample size.
The null hypothesis = 750 grams,
The alternative hypothesis= less than 750 grams.
so we need to calculate the test as:
t = (746 - 750) / (8 / √(20)) = -2.236
Next, we have to find the critical t-value for a one-tailed test with 19 degrees of freedom (so n-1 =19)
When you a t-distribution table, the critical t-value to be -1.734.
Therefore, know that -2.236 < (less than) -1.734, so you will reject the null hypothesis and say that the mean weight is less than 750 grams at a 10% significance level.
Learn more about hypothesis from
https://brainly.com/question/606806
#SPJ1


right cylinder calc: find r, h=10, v=n/a
Answers
if the volume is known, you can calculate the radius using the formula and the given values and it is =1.7853
To find the radius (r) of a right cylinder with a given height (h) of 10 and an unknown volume (V), additional information is needed to solve the problem. Without knowing the value of the volume, it is not possible to determine the exact value of the radius. The volume of a right cylinder is calculated using the formula V = \(\pi r^{2h}\), where π is a constant value approximately equal to 3.14159.
However, if you have the value of the volume (V), you can rearrange the formula to solve for the radius (r). For example, if the volume is given as V = 100 cubic units, you can use the formula V = πr^2h and substitute the known values to find the radius. Rearranging the formula, we get r = √(V / (πh)), where √ denotes the square root.
By plugging in the values of V = 100 and h = 10 into the formula, we can calculate the radius as r = √(100 / (π × 10)). Simplifying further, r ≈ √(10 / π) ≈ √(10 / 3.14159) ≈ √(3.1831) ≈ 1.7853
learn more about volume here:
https://brainly.com/question/28058531
#SPJ11
Let f(x) be the probability density function for a normal distribution N(68,5). Answer the following: (a) At what x value does f(x) reach a maximum? Maximum height: x (b)Does f(x) touch the x-axis at μ±30 ? No Yes
Answers
The probability density function for a normal distribution N(68, 5) reaches its maximum height at x = 68, which is the mean of the distribution. The function does not touch the x-axis at μ±30.
The probability density function (PDF) for a normal distribution is bell-shaped and symmetrical around its mean. In this case, the mean (μ) is 68, and the standard deviation (σ) is 5.
(a) To find the x value at which the PDF reaches a maximum, we look at the mean of the distribution, which is 68. The PDF is highest at the mean, and as we move away from the mean in either direction, the height of the PDF decreases. Therefore, the x value at which f(x) reaches a maximum is x = 68.
(b) The PDF of a normal distribution does not touch the x-axis at μ±30. The x-axis represents the values of x, and the PDF represents the likelihood of those values occurring. In a normal distribution, the PDF is continuous and never touches the x-axis. However, the PDF becomes close to zero as the values move further away from the mean. Therefore, the probability of obtaining values μ±30, which are 38 and 98 in this case, is very low but not zero. So, the PDF does not touch the x-axis at μ±30, but the probability of obtaining values in that range is extremely small.
Learn more about probability density function here: https://brainly.com/question/31039386
#SPJ11
If a procedure meets all of the conditions of a binomial distribution except the number of trials is not fixed, then the geometric distribution can be used. The probability of getting the first success on the xth trial is given by P(x) = p(1-p)x-1, where p is the probability of success on any one trial. Subjects are randomly selected for a health survey. The probability that someone is a universal donor (with group O and type Rh negative blood) is 0.14. Find the probability that the first subject to be a universal blood donor is the seventh person selected. C The probability is (Round to four decimal places as needed.) Assume that different groups of couples use a particular method of gender selection and each couple gives birth to one baby. This method is designed to increase the likelihood that each baby will be a girl, but assume that the method has no effect, so the probability of a girl is 0.5. Assume that the groups consist of 24 couples. Complete parts (a) through (c) below. -C a. Find the mean and the standard deviation for the numbers of girls in groups of 24 births. The value of the mean is μ =. (Type an integer or a decimal. Do not round.) The value of the standard deviation is o= (Round to one decimal place as needed.) b. Use the range rule of thumb to find the values separating results that are significantly low or significantly high. Values of girls or fewer are significantly low. (Round to one decimal place as needed.) Values of girls or greater are significantly high. is effective. (Round to one decimal place as needed.) is not effective. c. Is the result of 22 girls a result that is significantly high? What does it suggest about the effectiveness of the method? ▼ girls. A result of 22 girls would suggest that the method The result significantly high, because 22 girls is (Round to one decimal place as needed.)
Answers
When a procedure meets all of the conditions of a binomial distribution except the number of trials is not fixed, the geometric distribution can be used.
Given that subjects are randomly selected for a health survey, the probability that someone is a universal donor (with group O and type Rh negative blood) is 0.14.
We have to find the probability that the first subject to be a universal blood donor is the seventh person selected.Using the formula mentioned above:\(P(7) = 0.14(1 - 0.14)6= 0.0878\)
The probability is 0.0878. Option C is correct.
Now, let's solve the next part.Assuming that different groups of couples use a particular method of gender selection and each couple gives birth to one baby.
This method is designed to increase the likelihood that each baby will be a girl, but assume that the method has no effect, so the probability of a girl is 0.5.
Assuming that the groups consist of 24 couples.
(a)Find the mean and the standard deviation for the numbers of girls in groups of 24 births:
Let X be the number of girls in a group of 24 births.
\(X ~ B(24, 0.5)Mean:μ = np= 24 * 0.5= 12\)Standard deviation:\(σ = `sqrt(np(1-p))`= `sqrt(24*0.5*0.5)`= `sqrt(6)`≈ 2.449\) (rounded to one decimal place).
To know more about distribution visit:
https://brainly.com/question/29664127
#SPJ11
if we compute a 95onfidence interval 12.65 ≤ μ ≤ 25.65 , then we can conclude that.
Answers
Based on the computed 95% confidence interval, we can conclude that we are 95% confident that the true population mean falls within the range of 12.65 to 25.65.
A confidence interval is a range of values that provides an estimate of the true population parameter. In this case, we are interested in estimating the population mean (μ). The 95% confidence interval, as mentioned, is given as 12.65 ≤ μ ≤ 25.65.
Interpreting this confidence interval, we can say that if we were to repeat the sampling process many times and construct 95% confidence intervals from each sample, approximately 95% of those intervals would contain the true population mean.
The confidence level chosen, 95%, represents the probability that the interval captures the true population mean. It is a measure of the confidence or certainty we have in the estimation. However, it does not guarantee that a specific interval from a particular sample contains the true population mean.
Therefore, based on the computed 95% confidence interval, we can conclude that we are 95% confident that the true population mean falls within the range of 12.65 to 25.65.
Learn more about confidence interval here:
https://brainly.com/question/13067956
#SPJ11
Let P be some predicate. Check the box next to each scenario in which ∀n ∈ N, P(n) must be true.
a) For every natural number k > 0 , if P(i) holds for every natural number i < k, then P(k) holds.
b) P(0) holds and for every natural number k > 0, if P(i) does not hold, then there is some natural number i < k such that P(i) does not hold.
c) For every natural number k, if P(i) holds for every natural number i < k, then P(k) holds.
d) For every natural number k, if P(k) does not hold, then there is a smaller natural number i < k such that P(i) does not hold.
Answers
Answer:
A
Step-by-step explanation:
a) ✔️
This is the principle of mathematical induction. If P holds for the base case k=1 and we can show that if it holds for any arbitrary k (e.g. k=n) then it must also hold for the next value (e.g. k=n+1), then we have shown it holds for all natural numbers.
b) ❌
There is no guarantee that P holds for all natural numbers from the statement alone. It only guarantees that for any k where P does not hold, there exists a smaller number i where P does not hold.
c) ❌
This is the principle of weak mathematical induction. It only shows that if P holds for a given k and for all smaller values i then it must hold for k+1. It does not guarantee that P holds for all natural numbers.
d) ❌
This statement is the negation of the principle of mathematical induction. It is known as the "strong induction" principle, which assumes that if P does not hold for k, then there exists a smaller i where P does not hold. However, this principle is not sufficient to prove that P holds for all natural numbers k.
For the function f (x) = 5 - 7x, find the difference quotient .
Answers
f
(
x
+
h
)
−
f
(
x
)
h
Find the components of the definition.
Tap for more steps...
f
(
x
+
h
)
=
−
7
h
−
7
x
+
5
f
(
x
)
=
5
−
7
x
Plug in the components.
f
(
x
+
h
)
−
f
(
x
)
h
=
−
7
h
−
7
x
+
5
−
(
5
−
7
x
)
h
Simplify.

(1 point) evaluate the line integral ∫cf⋅d r where f=⟨−4sinx,5cosy,10xz⟩ and c is the path given by r(t)=(t3,t2,−2t) for 0≤t≤1
Answers
We are given a path c, and a vector field f. The path c is defined by r(t) = (t³, t², -2t) for 0 ≤ t ≤ 1. The vector field f = (-4sin x, 5cos y, 10xz). We are required to evaluate the line integral ∫cf ⋅ dr using the given information.To evaluate the line integral, we use the following formula:∫cf ⋅ dr = ∫abf(r(t)) ⋅ r'(t) dt.
Here, we can see that r(t) is already in vector form, so we don't need to convert it. We just need to find r'(t).Differentiating r(t) with respect to t, we get:r'(t) = (3t², 2t, -2)Substituting the given values of f and r'(t), we get:∫cf ⋅ dr = ∫₀¹ (-4sin t³, 5cos t², -20t³) ⋅ (3t², 2t, -2) dt= ∫₀¹ (-12t⁴ sin t³ + 10t cos t² - 20t⁴) dt= (-3t⁴ cos t³ + 5t³ sin t² - 5t⁵) from 0 to 1= -3 cos 1 + 5 sin 1 - 5The final answer is -3 cos 1 + 5 sin 1 - 5.
To know more about vector visit :-
https://brainly.com/question/24256726
#SPJ11
Find the length of the lamppost to the nearest inch.
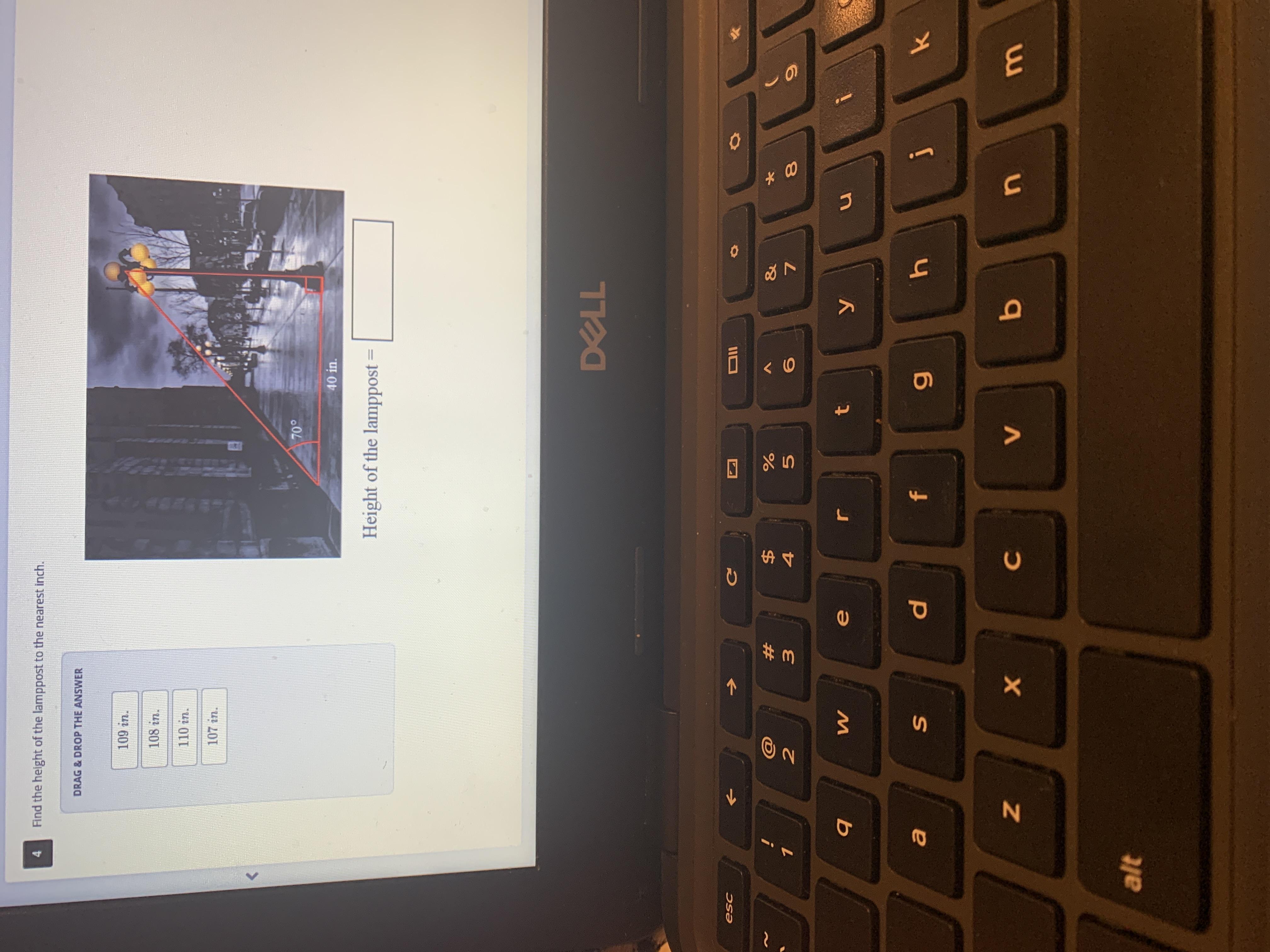
Answers
Answer:
109 inch
Step-by-step explanation:
we know that
\(tan\theta=\frac{Perp}{Base} \\\theta=70\\Base=40 in\)
So,
\(tan(70)=\frac{Perp}{40} \\\\2.747=\frac{Perp}{40} \\\\2.747\times40=Perp\\\\Perp=109\quad in\)
So, length of lamppost is 109 inch
Two rectangular picture frames have the same area of 45 square inches but have different side lengths. Frame A has a length of 6 3/4 inches, and Frame B has a length of 7 1/2 inches.
Without calculating, predict which frame has the shorter width. Explain your reasoning
Answers
Answer:
Frame B has the shorter width.
Step-by-step explanation:
The area of a rectangle is given by length×width. If the two have a maintained area of 45 in², then length and width are inversely proportional, meaning if one goes up, the other must go down. Since Frame B has a larger length than Frame A and both frames have the same area, Frame B must have a shorter width to accommodate for its larger length.
After a snowball fight, Stanley wanted to warm up with a cup of hot chocolate. He decided to make enough to share with his friends. First, he heated 6 cups of milk and 1 pint of cream in a large pot. Then, he stirred in 4 cups of melted chocolate. How many cups of hot chocolate did Stanley make?S
Answers
The total number of cups of chocolate is A = 12 cups
Given data ,
To find the total number of cups of hot chocolate that Stanley made, we need to add together the amounts of milk, cream, and melted chocolate.
6 cups of milk
1 pint of cream (1 pint = 2 cups)
On simplifying the equation ,
4 cups of melted chocolate
Now , the total number of cups is A
where A is
6 cups of milk + 2 cups of cream + 4 cups of melted chocolate = 12 cups of hot chocolate
Hence , Stanley made 12 cups of hot chocolate
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ1
PLS PLS HELP ASAP!!! ILL GIVE BRAINIEST AND 50 POINTS!!!
Identify or mark the missing side or angle that would make triangle ABC congruent to triangle PDF by AAS

Answers
Answer:
F and C
Step-by-step explanation:
CUZ AAS means angle angle side
Answer:
see explanation
Step-by-step explanation:
for the triangles to be congruent by the angle- side- angle (ASA postulate )
if two angles and the included side of one triangle are congruent to two angles and the included side of another triangle ( included side is the side between the vertices of the two angles ) , then the triangles are congruent.
given
∠ B ≡ ∠ D and AB ≡ PD
then the included sides are AB and PD
the other 2 angles for congruency are ∠ A ≡ ∠ P
-----------------------------------------------------
By the AAS postulate
If two angles and a non included side of one triangle are congruent to the corresponding parts of the other triangle, then the triangles are congruent
for AAS then ∠ C ≡ ∠ F
Determine if the expression -5y^5-y^3 is a polynomial or not. If it is a polynomial, state the type and degree of the polynomial.
Answers
Answer:
Yes, it is a polynomial, and the degree is 5
Step-by-step explanation:
A polynomial is a combination of terms separated using + or − signs and normally have exponents. So, this equation is a polynomial. The degree is just the highest exponential value, which is 5 because -5y is being raised to the 5th power
Answer this question. There are 3 answers
Answers
Answer:
uh?
Step-by-step explanation:
In the group of 2000 people 40 persent reads science and 30percent reads maths.If 100 people read both then how many people don't read both
Answers
Answer: 500 people don't read both.
Step-by-step explanation:
30% of 2,000 = 600 people read math.40% of 2,000 = 800 people read science.800 + 100 + 600 = 1,500 people either read science, math, or both.2,000 - 1,500 = 500 people don't read math and science.HELP DUE IN 15 MINS!
The center of a circle is (3, 2) and a point on the circle is (5, -2). Find the radius and write the equation for the circle.
Answers
Answer:
r = \(2\sqrt{5}\)
\((x - 3)^{2} + ( y - 2)^{2} = 20\)
Is this a live test question or a homework question?
Step-by-step explanation:
the radius is the distance between (3, 2) and (5, -2)
\(r^{2}\) = \({(3 - 5)^{2} + (2 + 2)^{2} }\)
= \((-2)^{2} + 4^{2}\)
= 4 + 16 = 20
r = \(\sqrt{20 } = 2\sqrt{5}\)
Equation of circle: \((x - 3)^{2} + ( y - 2)^{2} = 20\)
Answer:
Radius: \(2\sqrt{5}\)
Equation of circle: \((x-3)^2+(y-2)^2=20\)
Step-by-step explanation:
The radius of a circle is equal to the distance between the center of the circle and any point on the circle. Therefore, we have:
\(r=\sqrt{(5-3)^2+(2-(-2))^2},\\r=\sqrt{2^2+4^2},\\r=\sqrt{20}=\boxed{2\sqrt{5}}\)
The equation of a circle with radius \(r\) and center \((h, k)\) is given by:
\((x-h)^2+(y-k)^2=r^2\).
What we know:
radius of \(2\sqrt{5}\) center at \((3, 2)\)Substituting known values, we get:
\((x-3)^2+(y-3)^2=(2\sqrt{5})^2,\\\boxed{(x-3)^2+(y-2)^2=20}\)
When the function f(x) = 3(5)x is changed to f(x) = 3(5)x + 22, what is the effect? (4 points) There will be no change to the graph because the exponential portion of the function remains the same. The y-intercept is 22 spaces higher. The x‐intercept is 22 spaces higher. All input values are moved 22 spaces to the right.
Answers
Answer:
the y-intercept is 22 spaces higher.
Step-by-step explanation:
I don't know, what special operations you want to express with 3(5)x.
as it is written this simply means
3×5×x
no exponents or other special things are visible.
but it should not matter.
whatever is the first function is unchanged the first part of the second function.
so, the only difference is the "+ 22" part.
and that simply means that all y values (the functional result values) are increased by 22.
you know that "f(x) =" has the same meaning as "y =".
and with that also the y-intercept (the y value when x = 0, and therefore the point, where the curve intersects the y-axis) is increased by 22 spaces.
Is 4/7 a real number
Answers
Answer:
Yes, it is a real number.
Step-by-step explanation:
All numbers are real numbers.
What is the width of the rect-
angle that has an area of
1200 square feet and a length
of 40 feet?
Answers
Answer:
w = 30ft
1200 / 40 = 30
Select all sequences below that are bounded. There may be more
than one correct answer.
Group of answer choices
an=cos(n)
an=7n
an=(−8)^n
an=n/6n+1
an=1/12^n
Answers
A sequence is said to be bounded if its terms are limited to a certain value. The sequences that are bounded are Option a, option c, option e.
Let's go through the sequences and determine which ones are bounded:
a) an = cos(n): The cosine function oscillates between -1 and 1. As n increases, cos(n) will continue to fluctuate between these values. Therefore, an = cos(n) is bounded.
b) an = 7n: This sequence grows without bound as n increases. As n gets larger, the terms of the sequence become arbitrarily large. Thus, an = 7n is not bounded.
c) an = (-8)^n: When -8 is raised to an even power, the result is a positive number, and when it is raised to an odd power, the result is a negative number. In both cases, the magnitude of the number increases without bound as n increases. Therefore, an = (-8)^n is not bounded.
d) an = n/(6n + 1): To determine the behavior of this sequence, we can take the limit as n approaches infinity:
lim(n→∞) n/(6n + 1) = 1/6.
As n gets larger, the ratio n/(6n + 1) approaches the constant value of 1/6. Therefore, an = n/(6n + 1) is bounded.
e) an = 1/12^n: As n increases, the term 1/12^n becomes arbitrarily small. It will never be negative or exceed a certain value, such as 1. Therefore, an = 1/12^n is bounded.
So, the sequences that are bounded are:
an = cos(n)
an = n/(6n + 1)
an = 1/12^n
The sequences that are not bounded are:
an = 7n
an = (-8)^n
Learn more about bounded sequences at:
brainly.com/question/28819099
#SPJ11
There are five consecutive odd integers. The sum of the three last integers is 3 more than the sum of the two greatest.
Answers
Step-by-step explanation:
x
x+2
x+4
x+6
x+8
these are the 5 consecutive odd integers.
when starting with an odd number as x, with every added 2 we get again an odd number.
the sum of the last 3 integers is 3 more than the sum of the 2 greatest :
x+4 + x+6 + x+8 = x+6 + x+8 + 3
we can subtract (x+6) abd (x+8) from both sides :
x + 4 = 3
x = -1
so, the 5 numbers are
-1
1
3
5
7
3 + 5 + 7 = 15
5 + 7 + 3 = 15
correct.