Uma lousa digital possui uma forma retangular e tem sua largura expressa pelo polinômio b+2. Sendo sua área igual ao polinômio B ao quadrado + 5b+ 6, qual é o polinômio que expressa a altura dessa lousa?
Answers
Answer:
b+3
Step-by-step explanation:
Largura : b+2
Área: b² +5b +6
Sabe-se que a área de um retângulo é dada pela largura multiplicada pela altura.
A partir dos zeros da equação da área é possível encontrar o polinômio da altura:
\(b^2 +5b +6\\b=\frac{-5\pm \sqrt{25-4*1*6} }{2} \\b'=-2\\b''=-3\)
Visto que o polinômio da largura é b+2, para que a equação da área seja válida, o polinômio da altura deve ser b+3.
A prova pode ser feita pela multiplicação dos polinômios:
\(A = L*H\\A=(b+2)*(b+3)\\A=b^2+5b+6\)
Related Questions
A carpenter needs to cut 24-inch pieces of wood from a board that is 17 feet in length. What is the greatest number of 24-inch pieces the carpenter can cut from 6 of these boards of wood?
Answers
The greatest number of 24 inch pieces the carpenter can cut from 6 boards of wood is 51.
How to find the greatest number of 24 inches pieces that can be cut from the board?A carpenter needs to cut 24-inch pieces of wood from a board that is 17 feet in length.
Therefore, the greatest number of 24 inches pieces the carpenter can cut from 6 of these boards of wood can be calculated as follows:
let's convert from feet to inches.
17 feet = 204 inches
1 board = 204 inches
6 board = ?
cross multiply
length of 6 board = 204 × 6
length of 6 board = 1224 inches
Hence,
greatest number of 24 inch that can be cut from 6 boards = 1224 / 24
greatest number of 24 inch that can be cut from 6 boards = 51
learn more on length here: https://brainly.com/question/21415862
#SPJ1
which of these numbers are mutples of 7choose all that apply1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
Answers
Answer:
7, 14, 21
Step-by-step explanation:
We can get the multiples of 7 by multiplying them by numbers 1, 2, 3, ... and so on.
Add: 19|12 + 25|12 Simplify my Answer.
Answers
Answer:
8436
Step-by-step explanation:
19(|12+25|)(12)
=8436
____________ was designed to tabulate the 1890 census and used cards with designated areas representing data fields.
Answers
Answer:
Hollerith tabulating machine
Step-by-step explanation:
The Hollerith tabulating machine was invented by Herman Hollerith in other to assist in the data processing of the United States 1890 election. This machine was used to read and summarize the information stored on punchcards. This machine paved the way for the development of enhanced models which were employed for accounting and some other aspects related to business management.
Which sides (if any) are parallel?

Answers
The sides that are parallel include AB and DC.
What is a parallel sides?In geometry, parallel sides refer to two or more sides of a polygon or a pair of lines that never intersect and remain equidistant from each other at all points.
Parallelogram: A parallelogram is a quadrilateral with two pairs of parallel sides. Opposite sides of a parallelogram are parallel and congruent (equal in length).
Rectangle: A rectangle is a special type of parallelogram where all four angles are right angles (90 degrees). Opposite sides of a rectangle are parallel and congruent.
Rhombus: A rhombus is another type of parallelogram in which all four sides are congruent. Opposite sides of a rhombus are parallel.
Learn more about parallel sides on
https://brainly.com/question/24607467
#SPJ1
The surface area of a polyhedron can be found by:A. adding the total volume to the height.B. multiplying the perimeter of the base by the height and adding thearea of both bases.c. adding the lateral surface area to the area of one of the bases.D. multiplying the perimeter of the base by the length and adding thetotal volume.
Answers
To find the area of the polyhedron, we find the area of all faces of the polyhedron or the area covered by the net of the polyhedron
Considering all the options the lateral surface area is the area of the polyhedron without the area of the base. Therefore the surface area of a polyhedron can also be defined as the lateral surface area which is the area of every other face of the polyhedron except the base and then adding it to the area of one of the bases.
so option C
What are the domain and range of the inequality y < sqrt x+3+1
I don't get it I try to solve it but I just didn't get .

Answers
Given:
The inequality is:
\(y<\sqrt{x+3}+1\)
To find:
The domain and range of the given inequality.
Solution:
We have,
\(y<\sqrt{x+3}+1\)
The related equation is:
\(y=\sqrt{x+3}+1\)
This equation is defined if:
\(x+3\geq 0\)
\(x\geq -3\)
In the given inequality, the sign of inequality is <, it means the points on the boundary line are not included in the solution set. Thus, -3 is not included in the domain.
So, the domain of the given inequality is x>-3.
We know that,
\(\sqrt{x+3}\geq 0\)
\(\sqrt{x+3}+1\geq 0+1\)
\(y\geq 1\)
The points on the boundary line are not included in the solution set. Thus, 1 is not included in the range.
So, the domain of the given inequality is y>1.
Therefore, the correct option is A.
write a fracción and a decimal for the part of the gris that is shaded.

Answers
The shaded part is 3 column
There are 10 columnn in total.
The number of grids are 100 and shaded grids are 30
Thus the fraction of shaded portion is:
3/10.
The decimal form is 0.3.
If the range of 400 observed values has a high of 360kg and a low of 295kg, the best cell (or measurement) interval would be
Answers
The best cell (or measurement) interval for these 400 observed values with a range of 65 kg, a high of 360kg, and a low of 295kg is 3.25 kg.
The interval with the cells (or measurement) for a range of 400 observed values with a high of 360kg and a low of 295kg can be found as follows.Let's find the range of observed values first.
To find out the range, you need to subtract the smallest value (low) from the largest value (high) as given;
Range = High - Low = 360 - 295 = 65 kg
Now, we need to decide on the cell or measurement interval for these 400 observed values.
The measurement interval should not be too small or too large. If it is too small, the data may be over-detailed, and if it is too large, it may lose the essential information that we need.
Therefore, the measurement interval needs to be optimal and sufficient enough to provide the required information.Therefore, we need to calculate the number of intervals that would be suitable for this range.
One of the common ways to calculate the number of intervals is by using the square root of the number of observed values. So the number of intervals is:
No. of Intervals = sqrt (number of observed values) = sqrt(400) = 20 intervals
Now, we need to calculate the size of each cell or measurement interval
Size of interval = Range/No. of intervals = 65/20 ≈ 3.25 kg
Therefore, the best cell (or measurement) interval for these 400 observed values with a range of 65 kg, a high of 360kg, and a low of 295kg is 3.25 kg.
Learn more about measurement interval here https://brainly.com/question/27124916
#SPJ11
does applying gradient boosting linear regressor multiple times give the same result as linear regression
Answers
No, applying gradient boosting linear regressor multiple times does not necessarily give the same result as linear regression.
Gradient boosting is an iterative machine learning algorithm that involves combining multiple weak models, such as decision trees, to create a strong predictive model. In each iteration of the algorithm, a new model is trained to predict the errors of the previous models, and the final prediction is the sum of the predictions of all the models.
On the other hand, linear regression is a parametric method that involves fitting a linear equation to the data, where the coefficients of the equation are estimated using the least squares method. While gradient boosting linear regression and linear regression both aim to predict a target variable based on a set of input variables, they use different approaches and assumptions, and their results may not be the same.
In particular, gradient boosting can be more effective than linear regression when the relationship between the input variables and the target variable is nonlinear or when there are complex interactions between the input variables. However, linear regression can be more interpretable and easier to implement than gradient boosting in some cases.
To know more about linear regression,
https://brainly.com/question/29665935
#SPJ11
Problem 2 (21 points) The random variables X and Y have joint pdf fX,Y(x,y)=2e−x−y,0
Answers
1. P(X + Y ≤ 2) = -e⁻² - 2e⁻², 2. Marginal PDF for X: fₓ(x) = -2e⁻ˣ and marginal PDF for Y: fᵧ(y) = 2e⁻ʸ - 2e⁻ˣ⁻ʸ.
1. To find P(X + Y ≤ 2), we need to integrate the joint PDF over the region where X + Y is less than or equal to 2. Since X and Y are non-negative random variables, the region of interest is the triangle bounded by the lines X = 0, Y = 0, and X + Y = 2. Integrating the joint PDF over this region gives:
P(X + Y ≤ 2) = ∫∫ fₓᵧ(x, y) dx dy
The integral bounds can be determined by considering the constraints 0 ≤ X ≤ Y ≤ ∞:
0 ≤ x ≤ y
0 ≤ y ≤ ∞
Setting up the integral,
P(X + Y ≤ 2) = ∫[0,∞] ∫[x,2-x] 2e⁻ˣ⁻ʸ dy dx
Solving the integral,
P(X + Y ≤ 2) = ∫[0,∞] -2e⁻ˣ⁻ʸ ∣ x to 2-x dx
Simplifying the integral bounds,
P(X + Y ≤ 2) = ∫[0,∞] -2e⁻ˣ⁻²⁻ˣ + 2e⁻²⁻ˣ dx
Evaluating the integral,
P(X + Y ≤ 2) = -e⁻²⁻ˣ - 2e⁻²⁻ˣ ∣ 0 to ∞
As x approaches infinity, e⁻²⁻ˣ approaches 0, so the second term in the integral becomes zero.
P(X + Y ≤ 2) = -e⁻²⁻⁰ - 2e⁻²⁻⁰
P(X + Y ≤ 2) = -e⁻² - 2e⁻²
Therefore, P(X + Y ≤ 2) = -e⁻² - 2e⁻².
2. To find the marginal PDFs for X and Y, we integrate the joint PDF over the respective variable while treating the other variable as a constant. The marginal PDF for X, denoted as fₓ(x), is obtained by integrating the joint PDF fₓᵧ(x, y) over the range of Y:
fₓ(x) = ∫[x,∞] fₓᵧ(x, y) dy
Substituting the given joint PDF,
fₓ(x) = ∫[x,∞] 2e⁻ˣ⁻ʸ dy
Simplifying the integral,
fₓ(x) = -2e⁻ˣ⁻ʸ ∣ x to ∞
As y approaches infinity, e⁻ˣ⁻ʸ approaches 0, so the integral becomes,
fₓ(x) = -2e⁻ˣ⁻ˣ
Simplifying further,
fₓ(x) = -2e⁻ˣ
Therefore, the marginal PDF for X is fₓ(x) = -2e⁻ˣ.
Similarly, the marginal PDF for Y, denoted as fᵧ(y), is obtained by integrating the joint PDF fₓᵧ(x, y) over the range of X,
fᵧ(y) = ∫[0,y] fₓᵧ(x, y) dx
Substituting the given joint PDF,
fᵧ(y) = ∫[0,y] 2e⁻ˣ⁻ʸ dx
Simplifying the integral,
fᵧ(y) = 2e⁻ˣ⁻ʸ ∣ 0 to y
fᵧ(y) = 2e⁻ʸ - 2e⁻ˣ⁻ʸ
Therefore, the marginal PDF for Y is fᵧ(y) = 2e⁻ʸ - 2e⁻ˣ⁻ʸ.
To know more about Probability density function (PDF), visit,
https://brainly.com/question/30403935
#SPJ4
Complete question - Let the random variables X and Y have the joint PDF given below:
fₓᵧ(x, y) = 2e⁻ˣ⁻ʸ when 0 ≤ X ≤ Y ≤ ∞
fₓᵧ(x, y) = 0 otherwise.
1. Find P(X + Y ≤ 2)
2. Find the marginal PDF for X and Y.
A coach is buying snacks for 22 players at a soccer match. She pays a total of $77 to
buy each player a bottle of water and an energy bar. The price of one energy bar is $2.
Let w equal the price of a bottle of water. Write an equation that
represents the situation.
Answers
Answer: 22( w + 2 ) =77 and the amount of the water bottle would be 1.50
Step-by-step explanation: i dont know what to write??
graph the following state and show the a h and k values.
y=2(x+3)^2-4

Answers

Simplify 9x^0y^-3 write your answer using only positive exponents 
Answers
Answer:
9x/y³
Step-by-step explanation:
The simplification of the expression 9x⁰y⁻³ will be 9/y³.
What is the law of indices?Index (indices) in Maths is the power or exponent which is raised to a number or a variable.
In another word the mathematics of power or exponent of any number is called indices.
As per the given expression,
9x⁰y⁻³
By the law of indices that, \(x^{-m}\) = 1/\(x^{m}\)
9x⁰y⁻³ = 9x⁰ × 1/y³
⇒ 9(1)/y³ = 9/y³
Hence "The simplification of the expression 9x⁰y⁻³ will be 9/y³".
To learn more about indices,
https://brainly.com/question/170984
#SPJ2
Question in the picture (disregard the choice)
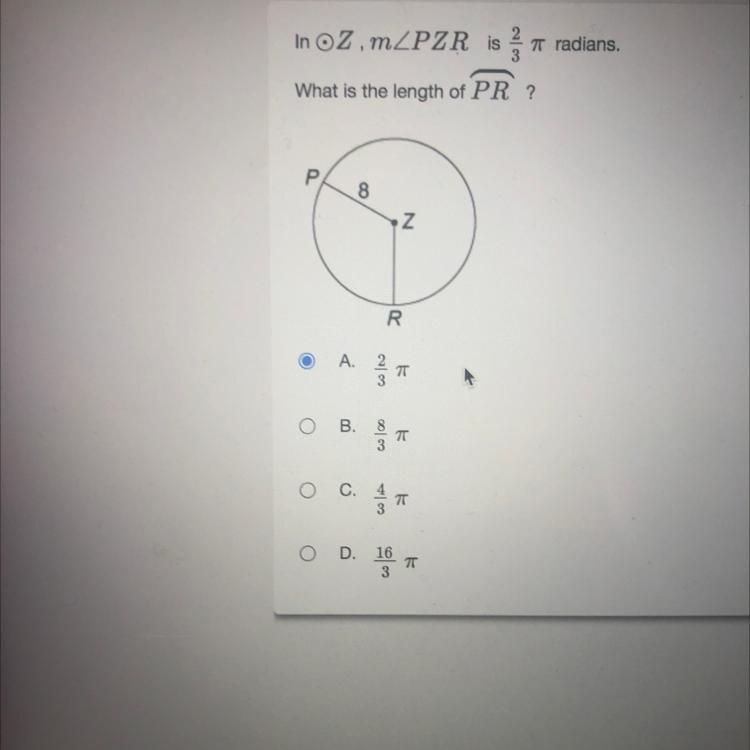
Answers
Answer:
D
Step-by-step explanation:
Answer:
A is the right answer of your question but....
I m little bit doubtful about that
if 4/5x - -3/4=0 then x=
Answers
a random sample of 22 people, the mean commute time to work was 34.2 minutes and the standard deviation was 7.1 minutes. assume the population is normally distributed and use a t-distribution to construct a 95% confidence interval for the population mean . what is the margin of error of y? interpret the results.
Answers
We're 95% confident that the true population mean is between 31.361 and 37.039 minutes, with a margin of error of 2.839 minutes.
To find the t-value from the t-distribution table, we need to know the degrees of freedom. Since we have a sample size of 22, the degrees of freedom are 22-1=21. Looking up the t-value with 21 degrees of freedom and a 95% confidence level, we get 2.080.
Plugging in this value, we get:
CI = 34.2 ± 2.080*(7.1/√22)
CI = 34.2 ± 2.839
Therefore, the 95% confidence interval for the population mean commute time to work is (31.361, 37.039). This means that if we were to take many random samples of size 22 from the population and construct a 95% confidence interval for each sample, 95% of those intervals would contain the true population mean.
The margin of error of y is the amount added and subtracted from the sample mean to get the upper and lower bounds of the confidence interval. In this case, the margin of error is 2.839 minutes.
This means that we're 95% confident that the true population mean commute time to work is between 31.361 and 37.039 minutes, with a margin of error of 2.839 minutes.
To know more about confidence interval here
https://brainly.com/question/24131141
#SPJ4
Re-do
-3 > 2/3p
Find inequality! :D
Answers
Answer:
p < -9/2 or p < -4.5
Step-by-step explanation:
-3 > 2/3p
-3 * 3> 2p
-9/2 > p
-9/2 > p or -4.5 > p
can y⁵ x y be simplified??
Answers
Answer:
Yes,
\(y^{6} x\)
Step-by-step explanation:
\(y^{5} xy = y^{5} *y*x = y^{6} x\)
The ratio of the number of bananas to the number of apples at a fruit stand is 3:5. Moe says that the ratio is equivalent to 12:25.
Answers
Answer: Moe is wrong.
Step-by-step explanation:
Moe is incorrect because 25 divided by 5 equals 5 (constant of proportionality) but 12 divided by 3 does not equal 5 (it equals 4)
Solve the system of equations.
- 5y + 87 = -18
5y + 2x = 58
X=
Y=
Answers
Answer:
Sorry, I tried.
Hope this helps.
Step-by-step explanation:
The chosen topic is not meant for use with this type of problem. Try the examples below.
6x2+3y2=126x2+3y2=12 , x+y=2x+y=2
x+2y=4x+2y=4 , x−y=−3x-y=-3
x2−y=2x2-y=2 , 2x−y=−12x-y=-1
-5y + 87 = -18
-5y = -18 - 87
-5y = -180
y = -180 / -5
y = +36
X:
( 5 x 36 ) + 2x = 58
180 + 2x = 58
2x = 58 - 180
2x = -122
x = -122 / 2
x = -61
According to my knowledge
Suppose that you must choose a password at your work that is five to seven characters long. How many possible passwords are there if: With 1his
i) each password can be any combination of alphanumeric characters ?
ii) each password must contain at least one digit? (The remaining characters are still able to be any alphanumeric value.)
Answers
The number of possible passwords for a length of 5 to 7 characters, where each character can be any alphanumeric value, is 218,340,105,584. If each password must contain at least one digit, then the number of possible passwords is 577,311,447,520.
There are 62 possible alphanumeric characters (26 uppercase letters + 26 lowercase letters + 10 digits). Therefore, the total number of possible passwords for a length of 5 to 7 characters is:
Total number of passwords = 62^5 + 62^6 + 62^7 = 218,340,105,584,896
If each password must contain at least one digit, then there are 10 choices for the first character, and 62 choices for each of the remaining four to six characters. Therefore, the total number of possible passwords is:
Total number of passwords = 10 * 62^4 + 10 * 62^5 + 10 * 62^6 = 577,311,447,520.
To know more about password, here
brainly.com/question/15577168
#SPJ4
pls help if you can asap!!!!

Answers
Answer: A
Step-by-step explanation: I would say A because the angle is greater than 90 degrees
Answer:
We have supplementary angles.
76 + 3x + 2 = 180
3x + 78 = 180
3x = 102
x = 34
suppose there is a 10% chance of raining, and there is a 2% chance that the midterm exam is cancelled. assume that these two events (raining and cancelling the exam) are independent. what is the probability that neither events happen? please select the best answer.
Answers
TLDR: 88%
The probability of neither event happening is the complement of the probability of either event happening, which is 100 - 12 = 88.
Cheers,
qxxi
PLS HELP WILL MARK BRAINLIEST!!!!!!!!
answer both questions (they are two separate questions)


Answers
Answer: c
Step-by-step explanation:
Can someone help me pls?

Answers
Isosceles triangles have 2 equal sides. In this case, the 6 foot side and the x/9 side are the same length. Set 6 equal to x/9 and solve:
6 = x/9
Multiply both sides by 9.
54 = x

match each decimal value on the left with the corresponding hexadecimal
Answers
To match decimal values with their corresponding hexadecimal values, we need to convert the decimal numbers into their hexadecimal equivalents using division and remainders.
To match each decimal value on the left with the corresponding hexadecimal value, we need to convert the decimal numbers into their hexadecimal equivalents.
Here are a few examples:
1. Decimal 10 = Hexadecimal A
To convert 10 to hexadecimal, we divide it by 16. The remainder is A, which represents 10 in hexadecimal.
2. Decimal 25 = Hexadecimal 19
To convert 25 to hexadecimal, we divide it by 16. The remainder is 9, which represents 9 in hexadecimal. The quotient is 1, which represents 1 in hexadecimal. Therefore, 25 in decimal is 19 in hexadecimal.
3. Decimal 128 = Hexadecimal 80
To convert 128 to hexadecimal, we divide it by 16. The remainder is 0, which represents 0 in hexadecimal. The quotient is 8, which represents 8 in hexadecimal. Therefore, 128 in decimal is 80 in hexadecimal.
Remember, the hexadecimal system uses base 16, so the digits range from 0 to 9, and then from A to F. When the decimal value is larger than 9, we use letters to represent the values from 10 to 15.In conclusion, to match decimal values with their corresponding hexadecimal values, we need to convert the decimal numbers into their hexadecimal equivalents using division and remainders.
Learn more about Equivalente here,https://brainly.com/question/2972832
#SPJ11
2.1 is what percent of 37?
O 1493.#%
O 1761.9%
O 5.7%
0 0.06%
Answers
if you need a step by step comment and i’d be happy to give one
is the following example true or false? if false give a counterexample. The sum of two rational numbers is always rational the sum of two irrational numbers is always irrational
Answers
Answer:
Both are TRUE.
Step-by-step explanation:
The sum of 2 rational numbers is always rational.
The sum of 2 irrational numbers is always irrational.
The sum of two rational numbers is always rational the sum of two irrational numbers is always irrational.
What are rational and irrational numbers?
Rational number are real numbers that can be expressed as a ratio of two integers.
Irrational number are real numbers that cannot be expressed as a ratio of two integers.
Now, to prove that,
The sum of two rational numbers is always rational.
Let us take an example,
Suppose two rational numbers sqrt(16) and sqrt(36),
So, there sum is given as,
sqrt(16) + sqrt(36) = 4 + 6
sqrt(16) + sqrt(36) = 9
which is rational.
Hence, the sum of two rational numbers is always rational.
The sum of two irrational numbers is always irrational
Let us take an example,
Suppose two irrational numbers sqrt(7) and pi,
So, there sum is given as,
sqrt(7) + pi = 5.7857...
This cannot be reduced to any kind of fraction
So, we will get an irrational number.
Thus, the sum of two irrational numbers is always irrational.
Hence, the sum of two rational numbers is always rational the sum of two irrational numbers is always irrational.
To learn more about rational and irrational numbers :
https://brainly.com/question/15267867
#SPJ2
The swimming pool shown is a right prism with concave hexagonal bases.... pls help

Answers
3 bottom sections:
10 x 20 = 200
5x 20 = 100
10 x 20 = 200
Bottom area = 200 + 200 + 100 = 500 square feet.
Short side: 3 x 20 = 60
Deep end wall : 6 x 20 = 120
Side wall : (24 x6) - (10x3) - (1/2 x 4x3) = 144-30-6 = 108
2 side walls: 108 x 2 = 216
Total area : 500 + 216 + 60 + 120 = 896 square feet
Divide total area by area of 1 gallon:
896/400 = 2.24 gallons
It will take 2.24 gallons of paint