Two marathon runners run the full distance of the marathon, approximately 26 miles, in 4 hours.
Part A
About how many miles did they run in 1 hour?
Enter the correct answer in the box. Part B
What percent of the full distance have they run in 1 hour?
Enter the correct answer in the box.
Answers
Answer:
6.5 miles in 1 hour and they will run 75% of the full distance in 1 hour.
Step-by-step explanation:
The distance covered by two marathon runners = 26 miles
They takes 4 hours
We need to find how many miles did they run in 1 hour
In 4 hour, the distance covered is 26 miles
To find distance covered in 1 hour, divide 26 by 4 such that.
\(d=\dfrac{26}{4}\\\\d=6.5\ \text{miles/hour}\)
So, they will cover 6.5 miles in 1 hour.
For percentage,
\(\%=\dfrac{26-6.5}{26}\times 100\\\\=75\%\)
So, they will run 75% of the full distance in 1 hour.
Related Questions
Select the correct answer.
The variable s varies directly as the square of t. When s= 4, t= 12. Nick's work finding the value of twhen s = 48 is shown:
s = kt2
12 = k : 42
12 = 16k
0.75 = k
48 = 0.752
64 = t2
8 = t
What is the first error, if any, in Nick's work?
OA. He did not make any errors.
ОВ. He used an equation that models inverse variation instead of direct variation.
OC. He substituted incorrectly when calculating the constant of variation.
OD.
He made an error when isolating t.

Answers
Its C. He substituted incorrectly when calculating the constant of variation.
Reason: He said so
The first error in Nick's work is he substituted incorrectly when calculating the constant of variation. The correct answer is C.
What is variable?The unknown term which is need to be calculated using system of equations is called variable.
Given s= 4, t= 12 to calculate value of k in the equation
s = kt²
4 = k (12)²
k = 0.02777
Thus, the first error he made is substituted incorrect values while calculating constant k.
Learn more about variable.
https://brainly.com/question/22277991
#SPJ5
Conduct a test to determine whether the two classifications R and C are independent, using the data
in the accompanying cross-classification table. (Use
α = .10.)
Applications
Use alpha 5% significance level unless specified otherwise
Answers
If the calculated chi-square statistic is greater than the critical value, reject the null hypothesis (i.e., conclude that the two classifications are not independent).
- If the calculated chi-square statistic is less than or equal to the critical value, do not reject the null hypothesis (i.e., we do not have enough evidence to conclude that the two classifications are not independent).
To determine if the two classifications R and C are independent, we will perform a chi-square test of independence using the data provided in the cross-classification table. Since the question asks us to use α = 0.10, we will use this significance level for our test, even though the default is Alpha 5%.
Follow these steps for the chi-square test:
1. Calculate the expected frequencies for each cell in the table, assuming R and C are independent. Use the formula:
Expected frequency = (Row total * Column total) / Grand total
2. Calculate the chi-square statistic using the formula:
χ² = Σ [ (Observed frequency - Expected frequency)² / Expected frequency ]
3. Determine the degrees of freedom (df) using the formula:
df = (number of rows - 1) * (number of columns - 1)
4. Compare the calculated chi-square statistic to the critical value from the chi-square distribution table, using the specified significance level (α = 0.10) and the calculated degrees of freedom.
5. Make a conclusion:
- If the calculated chi-square statistic is greater than the critical value, reject the null hypothesis (i.e., conclude that the two classifications are not independent).
- If the calculated chi-square statistic is less than or equal to the critical value, do not reject the null hypothesis (i.e., we do not have enough evidence to conclude that the two classifications are not independent).
Perform these steps using the data in the cross-classification table. Based on the results, you can determine whether the two classifications R and C are independent or not at the given significance level.
To learn more about data: https://brainly.in/question/48902948?referrer=searchResults
#SPJ11
Please help solve :D
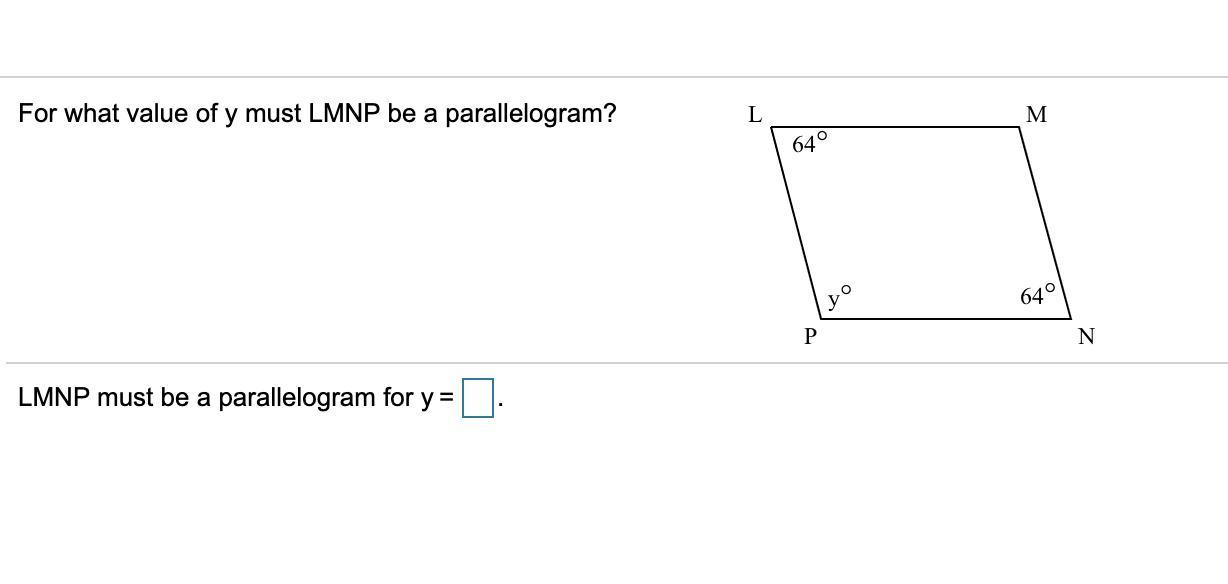
Answers
So y = 180-64 = 116 degrees
I need help solving this please

Answers
Consider these three numbers expressed in scientific notation: 8.2 × 10-3, 5.2 × 10-6, and 4.1 × 10-6. which number is the greatest, and by how many times is it greater than the smallest number? a. the greatest number is 8.2 × 10-3. it is 20 times greater than the smallest number. b. the greatest number is 5.2 × 10-6. it is 20 times greater than the smallest number. c. the greatest number is 8.2 × 10-3. it is 2,000 times greater than the smallest number. d. the greatest number is 5.2 × 10-6. it is 2,000 times greater than the smallest number.
Answers
C)The greatest number is 8.2 × 10-3. It is 2,000 times greater than the smallest number.
In scientific notation, a number is written as the product of a number between 1 and 10 and a power of 10. The power of 10 tells us how many places to move the decimal point to the right (if the exponent is positive) or to the left (if the exponent is negative).
In this case, 8.2 × 10-3 means 8.2 × (10^-3) = 0.0082, 5.2 × 10-6 means 5.2 × (10^-6) = 0.0000052 and 4.1 × 10-6 means 4.1 × (10^-6) = 0.0000041.
To compare the numbers, we can compare the coefficient or the number in front of the 10 power. We can see that 8.2 is greater than 5.2 and 4.1. To check how many times greater the smallest number is, we can use the following formula: (greatest number / smallest number) = (8.2 / 0.0000041) = 2,000
Therefore, the greatest number is 8.2 × 10-3 and it is 2,000 times greater than the smallest number.
For more questions like Scientific notation click the link below:
https://brainly.com/question/21289208
#SPJ4
]
can someone please help me I don’t understand what to do

Answers
So your equation should say
3x - 10 + 70 = 180
3x + 60 = 180
-60 -60
3x = 120
— —
3 3
X = 40
And your answers x = 40
Hope you understood
Please help me out, thank you! I'll be giving brainliest and five stars to the correct answer!
Find the lowest value of the set of data this box-and-whisker plot represents. (Look at the image)
16
12
15
13
Also, please put an explanation to your answer, thanks :)

Answers
Answer:
Step-by-step explanation:
The lowest value of the set of data in the boxplot is 12.
12 is the lowest as:
15 is the lower quartile.
16 is the median.
18 is the upper quartile.
20 is the highest value.
divide x³ + 5x² + 7x – 2 by x + 3.
Answers
Answer:
= x^3 + 5x^2 + 5x + 3
Step-by-step explanation:
Let's simplify: Step-by-Step.
x^3 + 5x^2 + 7x − 2x + 3
=x^3 + 5x^2 + 7x + − 2x + 3
Combine Like Terms:
=x^3 + 5x^2 + 7x + − 2x + 3
=(x^3) + (5x^2) + (7x + − 2x) + (3)
=x^3 + 5x^2 + 5x + 3
Answer:
=x^3 + 5x^2 + 5x + 3
HOPE THIS HELPS!
PLEASE MARK BRAINLIEST IF THIS HELPED YOU LEARN
Answer:
(x³ + 5x² + 7x – 2) /(x+3)=(x^2+2x+1)-5/(x+3)

Show that the quadrilateral is a parallelogram.

Answers
9514 1404 393
Answer:
opposite sides have the same slope, so it is a parallelogram
Step-by-step explanation:
A parallelogram has opposite sides that are parallel. Here, one pair of opposite sides consists of horizontal lines. Both have zero slope, so are parallel.
The other pair of lines each has a "rise" of 3 units for each "run" of 2 units, so the lines have a slope of 3/2. Both lines have the same slope, so are parallel.
Since opposite sides are parallel, the figure is a parallelogram.
The fifth grade has 152 students. Each student has 18
pencils. About how many pencils do the students have altogether?
Answers
There are total of 152 students in 5th grade, then the number of pencils altogether will be equal to 2,736 pencils.
What are arithmetic operations?The four basic operations of arithmetic can be used to add, subtract, multiply, or divide two or even more quantities.
They cover topics like the study of integers and the order of operations, which are relevant to all other areas of mathematics including algebra, data processing, and geometry.
As per the given information in the question,
Total number of students in 5th grade = 152
Amount of pencil each student have = 18
Then, the total number of pencils altogether,
= 152 × 18
= 2,736 pencils.
To know more about arithmetic operations:
https://brainly.com/question/13585407
#SPJ1
2. How many bits are needed to represent decimal values ranging from 0 to 12,500?
Answers
To represent decimal values ranging from 0 to 12,500, we need 14 bits.
To determine the number of bits needed to represent decimal values ranging from 0 to 12,500, we need to find the smallest number of bits that can represent the largest value in this range, which is 12,500.
The binary representation of a decimal number requires log base 2 of the decimal number of bits. In this case, we can calculate log base 2 of 12,500 to find the minimum number of bits needed.
log2(12,500) ≈ 13.60
Since we can't have a fraction of a bit, we round up to the nearest whole number. Therefore, we need at least 14 bits to represent values ranging from 0 to 12,500.
Using 14 bits, we can represent decimal values from 0 to (2^14 - 1), which is 0 to 16,383. This range covers the values 0 to 12,500, fulfilling the requirement.
Learn more about whole number
brainly.com/question/29766862
#SPJ11
pleasee help 100 points


Answers
Answer:
\(\begin{array}{| c | c |}\cline{1-2} x & y\\\cline{1-2} -3 & 0\\\cline{1-2} -2 & 1\\\cline{1-2} -1 & 2\\\cline{1-2} 0 & 3\\\cline{1-2} 1 & 4\\\cline{1-2} 2 & 5\\\cline{1-2}\end{array}\)
non-proportional
Step-by-step explanation:
Given equation:
\(y=x+3\)
Create a table of ordered pairs using the given equation:
\(\begin{array}{| c | c | c |}\cline{1-3} x & x+3 & y\\\cline{1-3} -3 & -3+3 & 0\\\cline{1-3} -2 & -2+3 & 1\\\cline{1-3} -1 & -1+3 & 2\\\cline{1-3} 0 & 0+3 & 3\\\cline{1-3} 1 & 1+3 & 4\\\cline{1-3} 2 & 2+3 & 5\\\cline{1-3}\end{array} \implies \begin{array}{| c | c |}\cline{1-2} x & y\\\cline{1-2} -3 & 0\\\cline{1-2} -2 & 1\\\cline{1-2} -1 & 2\\\cline{1-2} 0 & 3\\\cline{1-2} 1 & 4\\\cline{1-2} 2 & 5\\\cline{1-2}\end{array}\)
Graph
As the given equation is linear, plot two of the ordered pairs and draw a straight line through them. (See attachment).
Proportional Relationship
A relationship in which two quantities vary directly with each other.
y varies directly as x:
\(y=kx\)
(where k is some constant)
To find if the relationship is proportional using the table, find the ratio \(\dfrac{y}{x}\) of each row. If the ratio is the same, the relationship is proportional.
\(\begin{array}{| c | c | c |}\cline{1-3} x & y & \dfrac{y}{x}\\\cline{1-3} -3 & 0 & 0\\\cline{1-3} -2 & 1 & -0.5} \\\cline{1-3} -1 & 2 & -2 \\\cline{1-3} 0 & 3 & \text{-}\\\cline{1-3} 1 & 4 & 4\\\cline{1-3} 2 & 5 & 2.5\\\cline{1-3}\end{array}\)
Graphs of proportional relationships pass through the origin (0, 0).
Therefore, the relationship is non-proportional because:
The ratios of y/x of each row of the table are not the same.The graph does not pass through the origin.There is the addition of a constant in the given equation, which means that y does not vary directly as x.
Suppose that the production function is q=F(L,K)=(KL)
1/3
. The output and input prices are (p,w,r)=(1,1,1). ** Part a (5 marks) Derive the long-run cost function C(q). ** Part b (7 marks) Solve the long-run profit maximization problem directly: max
K,L
1∗F(L,K)−1∗L−1∗K and find the profit-maximizing output. [Hint: there are two first-order conditions, and you need to solve them jointly.] ** Part c (8 marks) As an alternative to Part b, solve for the profit-maximizing output using the longrun cost function you derived in Part a.
Answers
The long-run cost function is C(q) = 2w(sqrt[rw(q^3)]). The profit-maximizing output can be found by minimizing this cost function with respect to q.
Part a: Deriving the long-run cost function C(q):
To derive the long-run cost function, we need to find the minimum cost of producing a given output level q using the given production function.
Given the production function q = F(L, K) = (KL)^(1/3), we can rewrite it as K = (q^3)/L.
Now, let's express the cost function C(q) in terms of q. We have the cost function as C(q) = wL + rK, where w is the wage rate and r is the rental rate.
Substituting the expression for K in terms of q, we get C(q) = wL + r[(q^3)/L].
To minimize the cost function, we can take the derivative of C(q) with respect to L and set it equal to zero:
dC(q)/dL = w - r[(q^3)/(L^2)] = 0.
Simplifying the equation, we have w = r[(q^3)/(L^2)].
Solving for L, we get L^2 = r(q^3)/w.
Taking the square root, we have L = sqrt[(r(q^3))/w].
Substituting this value of L back into the cost function equation, we get:
C(q) = w(sqrt[(r(q^3))/w]) + r[(q^3)/sqrt[(r(q^3))/w]].
Simplifying further, we have:
C(q) = 2w(sqrt[rw(q^3)]).
So, the long-run cost function C(q) is given by C(q) = 2w(sqrt[rw(q^3)]).
Part b: Solving the long-run profit maximization problem directly:
To solve the profit maximization problem directly, we need to maximize the expression:
max K, L [F(L, K) - wL - rK].
Taking the derivative of the expression with respect to L and K, and setting them equal to zero, we can solve for the optimal values of L and K.
The first-order conditions are:
dF(L, K)/dL - w = 0, and
dF(L, K)/dK - r = 0.
Differentiating the production function F(L, K) = (KL)^(1/3) with respect to L and K, we get:
(1/3)(KL)^(-2/3)K - w = 0, and
(1/3)(KL)^(-2/3)L - r = 0.
Simplifying the equations, we have:
K^(-2/3)L^(1/3) - (3/2)w = 0, and
K^(1/3)L^(-2/3) - (3/2)r = 0.
Solving these two equations simultaneously will give us the optimal values of L and K.
Part c: Using the derived long-run cost function:
In Part a, we derived the long-run cost function as C(q) = 2w(sqrt[rw(q^3)]).
To find the profit-maximizing output, we can minimize the long-run cost function C(q) with respect to q.
Taking the derivative of C(q) with respect to q and setting it equal to zero, we can solve for the optimal value of q.
dC(q)/dq = w(sqrt[rw(q^3)]) + (3/2)w(q^2)/(sqrt[rw(q^3)]) = 0.
Simplifying the equation, we have:
(sqrt[rw(q^3)])^2 + (3/2)(q^2) =
0.
Solving this equation will give us the profit-maximizing output q.
Learn more about long-run cost function here :-
https://brainly.com/question/30882146
#SPJ11
mia has a certain amount of money. if she buys $4$ pens and $1$ pencil, she will have $\$5$ left over. if she buys $2$ pens and $2$ pencils, she will have $\$3$ left over. if edward arrives with the same amount of money as mia, together they can buy $7$ pens and $4$ pencils and spend all their money. if $a$ is the cost of one pen and $b$ is the cost of one pencil, compute the ordered pair $(a,b)$.
Answers
If 2 is the cost of one pen and 6 is the cost of one pencil, compute the ordered pair (2,6)
When Mia buys 4 pens and 1 pencil, she has $5 left; the number of dollars she starts with is 4a+b+5.
When she buys 2 pens and 2 pencils, she has $3 left; the number of dollars she starts with is 2a+2b+3.
Since those two expressions represent the same number, set them equal to each other and simplify to get an equation in a and b.
4a+b+5=2a+2b+3
2a-b=-2 [1]
They can purchase 7 pens and 4 pencils with their entire budget if Edward shows up with the same amount of money that Mia did.
The two of them have twice as much money as Mia did in the beginning, and they can buy 7 pens and 4 pencils with the money they have left over. To get a second equation in a and b, write an equation that says that and simplify it.
7a+4b = 8a+2b+10
a-2b=-10 [2]
solving both the equations 1 and 2:
2a-b = -2 - [1]
a-2b = -10 -[2]
a = 2 , b= 6
if 2 is the cost of one pen and 6 is the cost of one pencil, compute the ordered pair (2,6)
To learn more about equations:
https://brainly.com/question/29657983
4(a + 4) = 2(a + 10)
Someone solve pls.
Answers
Answer:
a=2
Step-by-step explanation:
4a+16=2a+20
2a=4
a=2
Answer:
The value of a is 2.
Step-by-step explanation:
First, you have to expand using distributive law :
\(4(a + 4) = 2(a + 10)\)
\(4a + 16 = 2a + 20\)
Next, you have to move all the common terms to one side :
\(4a - 2a = 20 - 16\)
\(2a = 4\)
Lastly, you have to solve it by dividing:
\(a = 4 \div 2\)
\(a = 2\)
Calculate the effective compound interest on £2000 at 5%
interest haft-yearly after 4
years.
Answers
The effective compound interest on £2000 at a 5% interest rate, compounded semi-annually for 4 years, amounts to £434.15.
To calculate the effective compound interest, we need to consider the formula for compound interest: A = P(1 + r/n)^(nt), where A is the final amount, P is the principal amount, r is the annual interest rate, n is the number of times interest is compounded per year, and t is the number of years.
In this case, the principal amount (P) is £2000, the annual interest rate (r) is 5%, the interest is compounded semi-annually (n = 2), and the duration is 4 years (t = 4).
First, we calculate the interest rate per compounding period: 5% divided by 2 equals 2.5%. Next, we calculate the total number of compounding periods: 2 compounding periods per year multiplied by 4 years equals 8 periods.
Now we can substitute the values into the compound interest formula: A = £2000(1 + 0.025)^(2*4). Simplifying this equation gives us A = £2434.15.
The effective compound interest is the difference between the final amount and the principal: £2434.15 - £2000 = £434.15.
Therefore, the effective compound interest on £2000 at a 5% interest rate, compounded semi-annually for 4 years, amounts to £434.15.
Learn more about compound interest here:
https://brainly.com/question/22621039
#SPJ11
Qué significa a^2 en matemáticas es la mi trabajo
Answers
In mathematics, "\(a^2\)" denotes the square of a number or variable "a." It is calculated by multiplying "a" by itself.
How to illustrate with an example4For example, if "a" is 5, then a^2 would be 5*5, which equals 25. When "a" represents a positive number, its square is always positive.
If "a" is negative, its square is still positive since a negative multiplied by a negative results in a positive.
In geometrical terms, if "a" represents the length of the side of a square, then a^2 represents the area of that square. This notation is part of the general concept of exponentiation.
Read more about exponents here:
https://brainly.com/question/13669161
#SPJ1
The Question in English
What does a^2 mean in mathematics
please help me out!!!

Answers
Answer:
-0.4
Step-by-step explanation:
K12 school showed me
HELP PLEASE :/ not too good in geometry sadly

Answers
Answer:
3rd option
Step-by-step explanation:
tanB = \(\frac{opposite}{adjacent}\) = \(\frac{AC}{BC}\) = \(\frac{2x+4}{x+3}\)
Please answer quickly !!

Answers
Answer: B
Step-by-step explanation:
There is no perfect square root for 0.4, there is a perfect square root for all other numbers though.
Answer:
And:- B
it is the irrational number
Temperature is an example of a variable that uses (select one):
1. the ordinal scale
2. the interval scale
3. either ordinal or ratio scale
4. the ratio scale
Answers
Temperature is a variable that uses (2) the scale interval and, according to physical theory, represents in the numerical form how hot or cold something is.
What is Temperature?The physical concept of temperature indicates in numerical form how hot or cold something is.
A thermometer is used to determine temperature.
One variable that makes use of the scale interval is temperature.
Thermometers are calibrated using a variety of temperature scales, which historically defined distinct reference points and thermometric substances.
The most popular scales are the Celsius scale, sometimes known as centigrade, with the unit symbol °C, the Fahrenheit scale (°F), and the Kelvin scale (K), with the latter being mostly used for scientific purposes.
One of the seven base units in the International System of Units is the kelvin (SI). The lowest point on the thermodynamic temperature scale is absolute zero, or zero Kelvin, or 273.15 °C.
Therefore, the temperature is a variable that uses (2) the scale interval and, according to physical theory, represents in the numerical form how hot or cold something is.
Know more about Temperature here:
https://brainly.com/question/24746268
#SPJ4
what does the following indicate in a genogram:
1. square
2. circle
3. solid horizontal line
4. broken line
5. X through a square/circle
6. solid verticle line
Answers
In a genogram, various symbols and lines represent different aspects of a person's familial relationships and attributes. Here's a breakdown of the symbols you mentioned:
1. Square: A square in a genogram indicates a male individual. It represents the person's gender and is used to distinguish between male and female family members.
2. Circle: A circle in a genogram indicates a female individual. It represents the person's gender and is used to distinguish between male and female family members.
3. Solid horizontal line: A solid horizontal line in a genogram represents a marital relationship between two individuals. The line connects a square (male) and a circle (female) to show that they are married or in a committed partnership.
4. Broken line: A broken line in a genogram represents a non-blood relationship, such as an adoptive parent-child relationship or a step-sibling connection. It is used to show relationships that are not based on biological ties.
5. X through a square/circle: An X through a square or a circle indicates that the individual is deceased. This symbol is used to show that the person has passed away and is no longer living.
6. Solid vertical line: A solid vertical line in a genogram represents a parent-child relationship. It connects an individual (either a square or circle) to their parent(s), showing the biological connection between the family members.
These symbols and lines help provide a visual representation of a person's family history and relationships, making it easier to analyze and understand the various connections within a family tree.
Overall, a genogram is a visual representation of a family tree that includes important information about relationships, health issues, and other relevant details. By understanding the various symbols and indicators used in a genogram, it is possible to gain a deeper understanding of family dynamics and relationships, as well as potential risk factors for various health conditions. As such, genograms are an important tool for healthcare providers, therapists, and other professionals working with individuals and families.
Learn more about genogram here: brainly.com/question/29573143
#SPJ11
which of the internet protocols contains the ip address? group of answer choices tcp smtp all of the other answers internet protocol
Answers
The internet protocol that contains the IP address is the Internet Protocol (IP), the correct option is Internet protocol. The other options, TCP and SMTP, are protocols that operate on top of IP and do not contain the IP address themselves.
The correct answer is the Internet Protocol (IP). IP is responsible for delivering packets of data from the source to the destination based on IP addresses, while other protocols like TCP and SMTP handle different aspects of data transmission and communication.
Therefore, the correct option is Internet protocol.
To know more about internet protocol refer here:
https://brainly.com/question/30547558#
#SPJ11
Pls help me ill give brainlyest to first correct answer! pls and thank u!


Answers
Answer:
1 1/6
Step-by-step explanation:
the answer is 1 1/6
Answer:
for the first one, it is c. the second one is b
Step-by-step explanation:
Algebra II please help!

Answers
Answer:
D) a8 = 35 - (n - 1)(3)
Step-by-step explanation:
Make and test a conjecture about the quotient of a number and its reciprocal the quotient of a number and its reciprocal is?
Answers
We conclude that the conjecture that the quotient of a number and its reciprocal is always equal to 1 is not correct.
How to determine if the conjecture that the quotient of a number and its reciprocal is always equal to 1Conjecture: The quotient of a number and its reciprocal is always equal to 1.
To test this conjecture, let's consider a specific number, x, and its reciprocal, 1/x.
According to the conjecture, the quotient of x and its reciprocal should be 1.
Let's perform the calculation:
\(x / (1/x) = x * x/1 = x^2\)
Based on the calculation, we see that the quotient of x and its reciprocal simplifies to x^2, not necessarily equal to 1. Therefore, the conjecture is not true in general.
Hence, we conclude that the conjecture that the quotient of a number and its reciprocal is always equal to 1 is not correct.
Learn more about conjecture at https://brainly.com/question/14392383
#SPJ4
If z is inversely proportional to r, and z=32 when r=1.5, find r when z=8.
Answers
Answer:
votes
z is inversly proportional to r then z = k/r
zr = k
If z = 32 when r = 1.5
32(1.5) = k
48 = k
k = 48
If z = 8 then r = ?
8r = k
8r = 48
Divide to each side by 8.
r = 48/8
r = 6
In Problems 55-62, write each function in terms of unit step functions. Find the Laplace transform of the given function 0 =t< 1 57. f(t) = {8 12 1 Jo, 0 =t < 30/2 58. f(t) = ( sint, t = 30/2
Answers
The Laplace transform of the given function is,
L{f(t)} = (8/s) - 4e^{-3s/2}/s - 6e^{-2s}/s
Given function is f(t) = {8 12 1 Jo, 0 ≤ t < 3/2, 3/2 ≤ t < 2, 2 ≤ t < ∞ respectively.
We have to find Laplace transform of the given function.
For first interval 0 ≤ t < 3/2,
f(t) = 8u(t) - 8u(t-3/2)
For second interval 3/2 ≤ t < 2,
f(t) = 12u(t-3/2) - 12u(t-2)
For third interval 2 ≤ t < ∞,
f(t) = Jo(u(t-2))
Hence, we can write the Laplace transform of the given function as,
L{f(t)} = L{8u(t) - 8u(t-3/2)} + L{12u(t-3/2) - 12u(t-2)} + L{Jo(u(t-2))}
Where, L is Laplace transform.
Let's calculate each Laplace transform stepwise,
1. L{8u(t) - 8u(t-3/2)}L{8u(t)} = 8/L{u(t)}L{u(t)}
= 1/sL{u(t-3/2)}
= e^{-3s/2}/s
Therefore,
L{8u(t) - 8u(t-3/2)} = 8[1/s - e^{-3s/2}/s]
2. L{12u(t-3/2) - 12u(t-2)}L{12u(t-3/2)}
= 12e^{-3s/2}/sL{12u(t-2)}
= 12e^{-2s}/s
Therefore,
L{12u(t-3/2) - 12u(t-2)} = 12[e^{-3s/2}/s - e^{-2s}/s]
3. L{Jo(u(t-2))}L{Jo(u(t-2))} = ∫_{0}^{∞}δ(t-2)e^{-st}dtL{Jo(u(t-2))}
= e^{-2s}
Hence, the Laplace transform of the given function is,
L{f(t)} = 8[1/s - e^{-3s/2}/s] + 12[e^{-3s/2}/s - e^{-2s}/s] + e^{-2s}
= (8/s) - 4e^{-3s/2}/s - 6e^{-2s}/s
To know more about Laplace visit:
https://brainly.com/question/30759963
#SPJ11
11. Engineering The maximum load for a certain elevator is 2000 pounds. The total
weight of the passengers on the elevator is 1400 pounds. A delivery man who weighs
243 pounds enters the elevator with a crate of weight w. Write, solve, and graph an
inequality to show the values of w that will not exceed the weight limit of the elevator.
Answers
The inequality to show the values of [w] that will not exceed the weight limit of the elevator is w + 1643 ≤ 2000. On solving the inequality, we get w ≤ 357. The graph of the inequality is attached.
What is inequality?In mathematics, an inequality is a relation which makes a non-equal comparison between two numbers or other mathematical expressions. It is used most often to compare two numbers on the number line by their size.An inequality is a mathematical relationship between two expressions and is represented using one of the following -≤ : less than or equal to
≥ : greater than or equal to
< : less than
> : greater than
≠ : not equal to
Given is the maximum load for a certain elevator is 2000 pounds. The total weight of the passengers on the elevator is 1400 pounds. A delivery man who weighs 243 pounds enters the elevator with a crate of weight [w].
We can write the inequality as follows -1400 + 243 + w ≤ 2000
w + 1643 ≤ 2000
Solving the inequality, we get -w + 1643 ≤ 2000
w ≤ 2000 - 1643
w ≤ 357
Refer to the graph attached.Therefore, the inequality to show the values of [w] that will not exceed the weight limit of the elevator is w + 1643 ≤ 2000. On solving the inequality, we get w ≤ 357. The graph of the inequality is attached.
To solve more questions on inequalities, we get -
https://brainly.com/question/11897796
#SPJ1

Write the question of the line with the given slope and Y-intercept
Slope = 5
y-intercept =8
Answers
Answer:
y = 5x+8
Step-by-step explanation:
I'm assuming you mean to write an equation.
Slope intercept form is y = mx+b
m represents slope
b represents the y intercept
Substitute the values into the equation
We get: y = 5x+8