Two circles, C1 and C2, intersect at point A and B. Passes through the center O of circle C2. The point P lies on circle C2 so that the line PAT is target to circle Ci and point A. Let ∠APB =.
Answers
The value of ∠APB = 180°. It is a straight line.
Given the information, we can deduce that the line passing through the center O of circle C2 and point A also passes through point B, as AB is the intersection of the two circles.
Now, consider the line segment AP. Since PAT is tangent to circle C1 at point A, we know that ∠APT = 90°. Additionally, since AB is a diameter of circle C1, we know that ∠ABP = 90°.
Using these angles, we can see that ∠APB is equal to the sum of ∠APT and ∠ABP. Therefore,
∠APB = ∠APT + ∠ABP = 90° + 90° = 180°.
So, we have shown that ∠APB is a straight line.
To know more about circles, refer to the link below:
https://brainly.com/question/11253017#
#SPJ11
Related Questions
choose the statement that best describes what is meant when we say that the sample mean is unbiased when estimating the population mean.
Answers
The sample mean does not consistently overestimate or underestimate the population mean. It provides an accurate estimate of the population mean.
The statement that best describes what is meant when we say that the sample mean is unbiased when estimating the population mean is that the sample mean is equal to the population mean on average. In other words, the sample mean does not consistently overestimate or underestimate the population mean. It provides an accurate estimate of the population mean.
Learn more about mean :
https://brainly.com/question/19538277
#SPJ11
circle the expression that is equivalent to x/5+x/10
3x/10 2x/15 x/25 x^2/50
Answers
Answer:
A. 3x/10
Step-by-step explanation:
\(\frac{x}{5}+\frac{x}{10}\)
Find a common denominator. The lowest common denominator is 10, so match the equations to fit that denominator.
\((\frac{x*2}{5*2})+\frac{x}{10}\\\frac{2x}{10}+\frac{x}{10}\)
Now that the denominators are the same, combine the fractions by adding the numerators.
\(\frac{3x}{10}\)
Your answer is a.
A paper is in the form of a rectangle ABCD in which AB= 18 cm and BC=14cm.A semicircular portion with BC as diameter is cut off. Find the area of the remaining paper (see in below figure)
Answers
Answer:
remaining portion is area= area of rectangle- area of semicircle
= 18*14 - 3.14*7^2
=252-154.86
=199.86cm^2
In the last couple of months, Jack has seen rabbits in his backyard on
12 days and no rabbits on 36 days. What is the approximate probability
that he will see rabbits in his yard tomorrow?
Answers
Answer:
12/36 can be simplifed to 1/3 so he has a 1/3's chance of seeing them or 33%
Step-by-step explanation:
:)
Answer:
1/4
Step-by-step explanation:
What Linear equation represents the graph?
y =3x + 6
y=3x - 6
y = -3x + 6
y = -3x -6

Answers
Answer:
y=-3x-6
Step-by-step explanation:
A cone has a radius and height of 15 inches. What is the volume of the cone?
Answers
Answer:
3532.5
Step-by-step explanation:
Here’s the equation you would followe
V=1/3h(3.14)r^2
H=height
R=radius
umbilical cord blood is a rich source of stem cells. which possible advance in biology would most likely be a result of performing research with an individual's banked cord blood?
A. Creation of a novel cancer cell line to test anticancer agents
B. Creation of a personalized cell replacement therapy for the donor
C. Creation of a skin graft for an unrelated burn victim
D. Creation of a culture to produce vitamin E
Answers
Answer:
The answer is A.
Step-by-step explanation:
The possible advance in the field of biology that would be a result of the stem cell research is: Creation of a novel cancer cell line to test anticancer agents.
What is a stem cell research?This is a type of research that is carried out by biogical researchers. The function of this type of research is to manipulate the different cells that are in the human body.
This research is done in order to specialize some body cells that can be used to treat different diseases.
Read more on research here: https://brainly.com/question/968894
#SPJ2
Send em answers in !! Plz & Thx need immediately maybe 30 minutes THX

Answers
Answer:
bad handwritting so i can't see it
Step-by-step explanation:
suppose you were to collect data for the pair of given variables in order to make a scatterplot. for the variables time spent on homework before an exam and the exam grade, which is more naturally the response variable and which is the explanatory variable?
Answers
The time spent on homework will be naturally more an explanatory variable and exam grade a response variable.
The Linear equation for a scatter plot y = mx+b has two variables i.e., a Dependent Variable [Y] and an Independent variable [X] .
A student who spends more time on his work and do it nicely will automatically get good exam grade . On the other side, a student who did'nt dedicate much time to the homework and carelessly does it , will obviously score a low exam grade.We can see that the exam grade is dependent on the time spent on the homework which naturally makes exam grade a response variable and time spent on home a independent thus an explanatory variable.
Hence, the time spent on homework will be naturally more an explanatory variable and exam grade a response variable.
To understand more about scatter plot refer -
https://brainly.com/question/14777758
#SPJ4
In developing patient appointment schedules , a medical centre wants to estimate the mean time that a staff member spends with each patient. How large a sample should be taken if the desired margin of error is 2 minutes at a 95 per cent level of confidence? How large a sample should be taken for a 99 per cent level of confidence ? Use a planning value for the population standard deviation of 8 minutes.
Answers
A. A sample size of 62 should be taken for a 95% level of confidence.
B. The sample size of 107 should be taken for a 99% level of confidence.
a. To estimate the sample size needed to estimate the mean time a staff member spends with each patient, we can use the formula for sample size calculation:
n = (Z^2 * σ^2) / E^2
Where:
n = required sample size
Z = Z-score corresponding to the desired level of confidence
σ = population standard deviation
E = desired margin of error
For a 95% level of confidence:
Z = 1.96 (corresponding to a 95% confidence level)
E = 2 minutes
σ = 8 minutes (population standard deviation)
Substituting these values into the formula:
n = (1.96^2 * 8^2) / 2^2
n = (3.8416 * 64) / 4
n = 245.9904 / 4
n ≈ 61.4976
Since we can't have a fraction of a sample, we round up the sample size to the nearest whole number. Therefore, a sample size of 62 should be taken for a 95% level of confidence.
b. For a 99% level of confidence:
Z = 2.58 (corresponding to a 99% confidence level)
E = 2 minutes
σ = 8 minutes (population standard deviation)
Substituting these values into the formula:
n = (2.58^2 * 8^2) / 2^2
n = (6.6564 * 64) / 4
n = 426.0096 / 4
n ≈ 106.5024
Rounding up the sample size to the nearest whole number, a sample size of 107 should be taken for a 99% level of confidence.
Learn more about sample size :
brainly.com/question/25894237
#SPJ11
if the variance of a normal population is 4, what is the probability that the variance of a random sample of size 10 exceeds 6.526? a. find the probability using the distribution tableb. find the probability using R
Answers
The probability that the variance of a random sample of size 10 exceeds 6.526 is approximately 0.0325.
a. To find the probability that the variance of a random sample of size 10 exceeds 6.526, we use the chi-squared distribution with degrees of freedom equal to n-1 = 9.
Using the chi-squared distribution table, we find that the critical value for a one-tailed test with alpha = 0.05 and 9 degrees of freedom is 16.919.
The test statistic for this problem is:
χ^2 = (n-1)s^2/σ^2 = 9(6.526)/4 = 14.7945
Since the test statistic (14.7945) is less than the critical value (16.919), we fail to reject the null hypothesis that the variance of the sample is less than or equal to 6.526. Therefore, the probability that the variance of a random sample of size 10 exceeds 6.526 is less than 0.05.
b. To find the probability using R, we can use the pchisq() function. The syntax is pchisq(q, df, lower.tail = FALSE), where q is the test statistic, df is the degrees of freedom, and lower.tail = FALSE specifies a one-tailed test.
The R code to find the probability is:
n <- 10
sigma_sq <- 4
s_sq <- 6.526
df <- n-1
test_stat <- (n-1)*s_sq/sigma_sq
p_val <- pchisq(test_stat, df, lower.tail = FALSE)
p_val
The output is:
[1] 0.03254215.
Therefore, the probability that the variance of a random sample of size 10 exceeds 6.526 is approximately 0.0325.
Learn more about probability here
https://brainly.com/question/13604758
#SPJ11
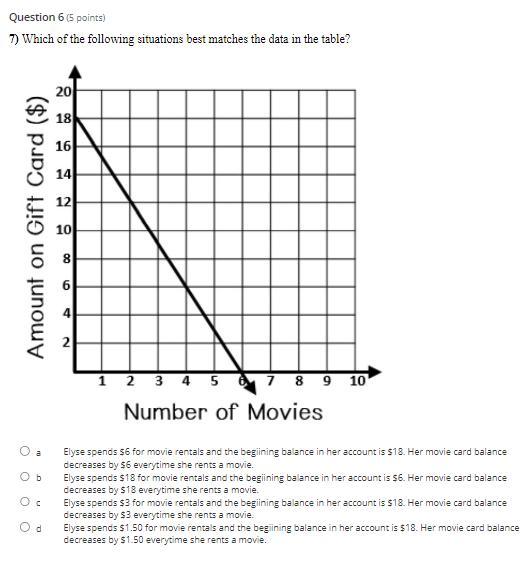
Which of the following situations best matches the data in the table?
Answers
Based on the graph, the situation that best matches what the data on the table shows is C. Elyse soends $3 for movie rentals and the beginning balance in her account is $18. Her movie card balance decreases by $3 everytime she rents a movie.
What does the data on the graph show?The data on the graph shows the amount of money that was spent by Elyse for every movie she rented. She did so with the use of a gift card. Based on the fact that the graph begins at $18, this means that the amount on the gift card was $18.
The amount that Elyse spent per movie was:
= Change in amount on gift card / Change in movies rented
= (18 - 12) / (2 - 0)
= 6 / 2
= $3
Elyse therefore spent $3 whenever she rented a movie.
Find out more on matching data at https://brainly.com/question/23957040
#SPJ1
HELP PLEASE
a rectangle room has an area of 400 square feet. the length is 7 feet less than twice the width. find the dimensions of the room.
Answers
Answer: 16 feet is the width and 25 is length
Step-by-step explanation:
x*(2x-7)=400
Word problem written in numerical form^^^^
Solve for x to get 16
length = 2(16)-7= 25
Check our work
16*25=400 yay
An open top box with a square bottom and rectangular sides is to have a volume of 256 cubic inches. Find the dimensions that require the minimum amount of material.
Answers
The dimensions that require the minimum amount of material are an 8-inch square bottom and a height of 4 inches using calculus.
To find the dimensions that require the minimum amount of material for an open-top box with a square bottom and rectangular sides and a volume of 256 cubic inches, we will use calculus.
1. Let x be the side length of the square bottom and y be the height of the box.
2. The volume, V = \(x^2 * y\). Since we are given that the volume is 256 cubic inches, we have x^2 * y = 256.
3. Solve for y: y = 256 / \(x^2\).
Now, let's find the surface area, which represents the material required.
4. The surface area, S = x^2 (square bottom) + 4 * x * y (four rectangular sides).
5. Substitute the expression for y we found earlier: S = \(x^2\) + 4 * x * (256 / \(x^2\)).
6. Simplify the surface area function: S = x^2 + (1024 / x).
Next, we'll minimize the surface area using calculus.
7. Differentiate the surface area function with respect to x: dS/dx = 2x - 1024 / \(x^2\).
8. Set the derivative equal to zero and solve for x: 2x - 1024 / \(x^2\) = 0.
9. Multiply both sides by x^2 to eliminate the fraction: 2\(x^3\) - 1024 = 0.
10. Solve for x: x^3 = 512, x = 8 inches.
Now, find the height (y) using the expression we found earlier:
11. y = 256 / \(x^2\) = 256 / \(8^2\) = 4 inches.
To learn more about calculus, refer here:
https://brainly.com/question/6581270#
#SPJ11
Sum and Product of zeroes of the quadratic polynomial 16s² - 16s + 4 respectively is:Sum and Product of zeroes of the quadratic polynomial 16s² - 16s + 4 respectively is:
Answers
Answer:
The sum and product of zeroes are 1 and 1/4, respectively.
Step-by-step explanation:
To determine the zeroes of the quadratic polynomial, let equalize the polynomial to zero and solve in consequence:
\(16\cdot s^{2}-16\cdot s + 4 = 0\)
By the General Quadratic Formula:
\(s_{1,2} = \frac{16\pm \sqrt{(-16)^{2}-4\cdot (16)\cdot (4)}}{2\cdot (16)}\)
\(s_{1,2} = \frac{1}{2}\)
Which means that zeroes are \(s_{1}=s_{2}=\frac{1}{2}\).
The sum and product of zeroes are, respectively:
\(s_{1}+s_{2} =\frac{1}{2}+\frac{1}{2}\)
\(s_{1}+s_{2} = 1\)
\(s_{1}\cdot s_{2} = \left(\frac{1}{2} \right)^{2}\)
\(s_{1}\cdot s_{2} = \frac{1}{4}\)
The sum and product of zeroes are 1 and 1/4, respectively.
2x^2 + 2y^2 - 8x + 10y + 2 =0
please help me with this problem. rewrite in standard form. find the center and radius of the circle. show all of your work.
Answers
Center of the circle is (-2, -1) and the radius is sqrt(23).
To rewrite the equation in standard form, we need to complete the square for both the x and y terms.
First, we can rewrite the equation as: 2x^2 - 8x + 2y^2 + 10y = -2
Next, we can add and subtract (8/2)^2 = 4 to complete the square for the x terms: 2x^2 - 8x + 4 + 2y^2 + 10y = -2 + 4
This simplifies to: (2x - 4)^2 + 2y^2 + 10y = 2
Then, we can add and subtract (10/2)^2 = 25 to complete the square for the y terms: (2x - 4)^2 + (5y + 5)^2 - 25 = 2 - 25
This simplifies to: (2x - 4)^2 + (5y + 5)^2 = -23
This is the equation in standard form: (x - h)^2 + (y - k)^2 = r^2
We can read the center of the circle as (h, k) = (-2, -1) and the radius as r = sqrt(23).
To show this, we can substitute the values back into the standard form equation: (x + 2)^2 + (y + 1)^2 = sqrt(23)^2
which simplifies to: (x + 2)^2 + (y + 1)^2 = 23
Thus, the center of the circle is (-2, -1) and the radius is sqrt(23).
To learn more about Equation if Circle,
Visit; brainly.com/question/29288238
#SPJ4
N is an interger what are the possible values of n A-, -2 ,-1, 0, 1, 2 ,3 ,4 ,5 ,6 B-, -1 ,1 ,2 ,3, 4, 5 ,6 C-, -2, -1 ,0 ,1, 2, 3 ,4, 5 D- ,-2 ,-1 ,0, 1 ,2, 3, 4, 5, 6, 7 E-, -1 ,0 ,1 ,2, 3 ,4 ,5 ,6
Answers
Answer:
All options have possible values of an integer
Explanation:
From the above options given all options are integers. An integer is a whole number, that is a number that is not a fraction or a decimal number. An integer can be negative, positive or zero such as the above given numbers. Here there are no fractions such as 1/4 or improper fractions as 1 3/4 or decimal numbers as 2.543, therefore all options are correct.
HELP!!!
Evaluate the function for x = 2
f(x)=7x-5
ISTG I WILL MARK BRAINLIEST!!!!
Answers
Answer:
9
Step-by-step explanation:
All you have to do is plug x = 2 into the equation so:
\(7 * 2 - 5\\14 - 5\\9\)
F(x)=7x-5
F(x)= 7(2)-5
=14-5
=11
Qa.) State the contrapositive of the following implication. If G is a connected planar graph then G has at least one vertex of degree <= 5.
Qb.) Prove the contrapositive stated in part (a). Hint: use the fact that if G is a connected Planar graph , then e <= 3v-6.
Qc.) Use part (a) to show that every planar graph can be colored with 6 (or less) colors. Hint: Use a proof by Induction on the number of vertices G.
Answers
We assume that G is a connected planar graph with no vertex of degree <= 5. We will use e <= 3v - 6 to prove that G is not a planar graph. By handshaking lemma, we know that 2e = sum of degrees of all vertices. Let d be the maximum degree of G.
Qa. Contrapositive of an implication is a new implication formed by negating both the hypothesis and the conclusion.
The contrapositive of the implication "If G is a connected planar graph, then G has at least one vertex of degree <= 5" is "If G has no vertex of degree <= 5, then G is not a connected planar graph."
Qb. Proof: We assume that G is a connected planar graph with no vertex of degree <= 5.
We will use e <= 3v - 6 to prove that G is not a planar graph. By handshaking lemma, we know that 2e = sum of degrees of all vertices.
Let d be the maximum degree of G. Since G has no vertex of degree <= 5, then d >= 6.
Thus, the sum of degrees of all vertices in G is greater than or equal to 6v/2, which is equal to 3v.
Hence, 2e >= 3v.
Substituting this inequality in e <= 3v - 6, we get 2e >= 3e - 6, which implies that e >= 6.
Since e >= 6, it follows that G is not planar.
Qc. Proof: We use proof by induction on the number of vertices of G. For a graph with one vertex, the statement is trivially true.
For a graph with n > 1 vertices, assume that every planar graph with at most n - 1 vertices can be colored with 6 (or less) colors.
Let G be a planar graph with n vertices.
By part (a), there exists a vertex v of G with degree <= 5.
We remove v and all its edges from G to get a new graph G' with n - 1 vertices.
By the induction hypothesis, we can color G' with 6 (or less) colors.
We add back v and its edges to G.
Since v has degree <= 5, at most 5 colors are used on its adjacent vertices.
We use a new color for v.
Thus, G can be colored with 6 (or less) colors.
Therefore, by induction, the statement is true for all planar graphs.
To know more about planar graph visit: https://brainly.com/question/30954417.
#SPJ11
Find the distance between point T (1,5) and point V (3,1). Round to the nearest tenth if necessary.
Please answer by Sunday
Answers
Answer:
use distance formula TV=root under (3-1)²+(1-5)² = root under 4+16=root 20
Step-by-step explanation:
3(a - 4) ≤ 33
Help me solve
Answers
Answer:
a ≤ 15
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightEquality Properties
Step-by-step explanation:
Step 1: Define
3(a - 4) ≤ 33
Step 2: Solve for a
Divide 3 on both sides: a - 4 ≤ 11Add 4 on both sides: a ≤ 15Here we see that any value a less than or equal to 15 would work as a solution to the inequality.
15PTS PLEASE HELP ASAP!
(dont write random answers pls)
look at the pic attached:

Answers
Answer:
-1.75
Step-by-step explanation:
We know that the midpoint formula is [for the x-coordinate per say] x = 1/2x1 + 1/2x2. If we want to find a point that lies 1/4th of the way we use x = 3/4x1 + 1/4x1. How? Because the point lies 1/4th from one endpoint and 3/4th from the other.
x = 3/4x1 + 1/4x2,
x = 3/4(-3) + 1/4(2) = -9/4 + 2/4 = -7/4
= - 1.75
--- There is an easier way to do it though, but it is really vague so you should not use it. We can form a triangle with MN being the hypotenuse. What would the length of the legs be? They would be 6 and 5. Now let's form a triangle 1/4th of that. 6/4 = 1.5 and 5/4 = 1.25. If you look at the diagram, start from point N move up 1.5 units and over 1.25 forming our mini triangle. You can see the x-axis has a value of -1.75.
Write tan 41π/36 in terms of the tangent of a positive acute angle.
Answers
tan(41π/36) can be written in terms of the tangent of a positive acute angle as (tan((1/9)π) + tan((37/36)π)) / (1 - tan((1/9)π)tan((37/36)π))
To express tan(41π/36) in terms of the tangent of a positive acute angle, we need to find an angle within the range of 0 to π/2 that has the same tangent value.
First, let's simplify 41π/36 to its equivalent angle within one full revolution (2π):
41π/36 = 40π/36 + π/36 = (10/9)π + (1/36)π
Now, we can rewrite the angle as:
tan(41π/36) = tan((10/9)π + (1/36)π)
Next, we'll use the tangent addition formula, which states that:
tan(A + B) = (tan(A) + tan(B)) / (1 - tan(A)tan(B))
In this case, A = (10/9)π and B = (1/36)π.
tan(41π/36) = tan((10/9)π + (1/36)π) = (tan((10/9)π) + tan((1/36)π)) / (1 - tan((10/9)π)tan((1/36)π))
Now, we need to find the tangent values of (10/9)π and (1/36)π. Since tangent has a periodicity of π, we can subtract or add multiples of π to get equivalent angles within the range of 0 to π/2.
For (10/9)π, we can subtract π to get an equivalent angle within the range:
(10/9)π - π = (1/9)π
Similarly, for (1/36)π, we can add π to get an equivalent angle:
(1/36)π + π = (37/36)π
Now, we can rewrite the expression as:
tan(41π/36) = (tan((1/9)π) + tan((37/36)π)) / (1 - tan((1/9)π)tan((37/36)π))
Since we are looking for an angle within the range of 0 to π/2, we can further simplify the expression as:
tan(41π/36) = (tan((1/9)π) + tan((37/36)π)) / (1 - tan((1/9)π)tan((37/36)π))
Therefore, tan(41π/36) can be written in terms of the tangent of a positive acute angle as the expression given above.
For more about tangent:
https://brainly.com/question/19064965
#SPJ4
Which function has real zeros at x = -10 and x = -67
Answers
Answer:
x^2 + 77x + 670 = 0
Step-by-step explanation:
x^2 + bx + c = 0
100 - 10b + c = 0
4489 - 67b + c = 0
4389 - 57b = 0
b = 77
100 - 770 + c = 0
c = 670
what does CRE mean in edge?
Answers
Solve the equation.
9x=25
Answers
Answer:
\(x = \frac{25}{9}\)
Step-by-step explanation:
Divide both sides by 9 to isolate x:
\(\frac{9x}{9} = \frac{25}{9} \\x = \frac{25}{9}\\\)
Hope this helps!
The measures of two angles of a triangle are 57° and 33°. Is the triangle acute, right, or obtuse? Use
geometric terms in your explanation,
Pls help !!
Answers
The triangle is a right angled triangle, because one angle of the triangle is a right angle, that is, it is exactly 90°.
Here, the measure of the two angles are given, so we can find the third angle using the angle sum property of a triangle
that is, 57° + 33° + x = 180°
= 90° + x = 180°
x = 180° - 90° = 90°
Since, the third angle is 90°, the triangle is a right angled triangle.
Solve 2x=54xˆ(2/3)
Please, I need the step by step working to find the value of x
Answers
Answer:
x = 19683 or x = 0
Step-by-step explanation:
Solve for x:
2 x = 54 x^(2/3)
Hint: | Isolate the radical to the left hand side by reversing the equality.
2 x = 54 x^(2/3) is equivalent to 54 x^(2/3) = 2 x:
54 x^(2/3) = 2 x
Hint: | Eliminate the power on the left hand side.
Raise both sides to the power of three:
157464 x^2 = 8 x^3
Hint: | Move everything to the left hand side.
Subtract 8 x^3 from both sides:
157464 x^2 - 8 x^3 = 0
Hint: | Factor the left hand side.
Factor x^2 and constant terms from the left hand side:
-8 x^2 (x - 19683) = 0
Hint: | Divide both sides by a constant to simplify the equation.
Divide both sides by -8:
x^2 (x - 19683) = 0
Hint: | Find the roots of each term in the product separately.
Split into two equations:
x - 19683 = 0 or x^2 = 0
Hint: | Look at the first equation: Solve for x.
Add 19683 to both sides:
x = 19683 or x^2 = 0
Hint: | Look at the second equation: Eliminate the exponent.
Take the square root of both sides:
Answer: x = 19683 or x = 0
An 8-ounce bottle of glue costs $1.92. What is the unit price
Answers
Answer:
$0.27 for 1 ounce
Step-by-step explanation:
Hope this helps!!!
simplify -3/5-(-1/10)
Answers
Answer:
-1/2
Step-by-step explanation:
Change the signs
-3/5 + 1/10
-6+1/10
-5/10
Reduce
-1/2
Answer:
-1/2
Step-by-step explanation:
Change the signs
-3/5 + 1/10
-6+1/10
-5/10
Reduce
-1/2