Twice a number increased by five is 11. What is the number?
Answers
Answer:
2
Step-by-step explanation:
Related Questions
7. Assume that when you take a bath, you fill a tub to the halfway point. The portion that you fill measures 6 feet by 2 feet by 2.2 feet. When you take a shower, your use a shower head with a flow rate of 2.23 gallons per minutes and you typically spend 8 minutes in the shower. There are 7.5 gallons in one cubic foot. a. Calculate the cubic feet of water for the bath. b. Calculate the cubic feet of water for the shower. C. How many minutes do you need in the shower to use as much water as the bath?
Answers
The volume of water filled in the bath tub is 6 feet × 2 feet × 2.2 feet = 26.4 cubic feet. You need 11.83 minutes in the shower to use as much water as the bath.
The volume of water filled in the bath tub is 6 feet × 2 feet × 2.2 feet = 26.4 cubic feet.
The amount of water used in shower = flow rate × time = 2.23 gallons/minute × 8 minutes = 17.84 gallons
Let's convert gallons to cubic feet: 1 cubic foot = 7.5 gallons
17.84 gallons = 17.84/7.5 cubic feet = 2.378 cubic feet
The volume of water used in the shower is 2.378 cubic feet. The volume of water used for taking a bath is 26.4 cubic feet.
To calculate how many minutes one would need in the shower to use as much water as the bath, divide the volume of water used in taking a bath with the amount of water used per minute in the shower as shown:
26.4/2.23=11.83 min
Therefore, one needs 11.83 minutes in the shower to use as much water as the bath.
To know more about volume, visit:
https://brainly.com/question/1578538
#SPJ11
Please answer fast! (10 points)
Type the correct answer in each box. Use numerals instead of words. If necessary, use / for the fraction bar(s).
Line m has no y-intercept, and its x-intercept Is (3, 0). Line n has no x-intercept, and its y-intercept Is (0, -4).
The equation of line m is ____
and the equation of line n is ____
Answers
Answer:
can u show me a picture of this problem.
Step-by-step explanation:
Help me please help

Answers
Answer:
165°
..
..
..
..
..
..
.............
how many faces does the following shape have
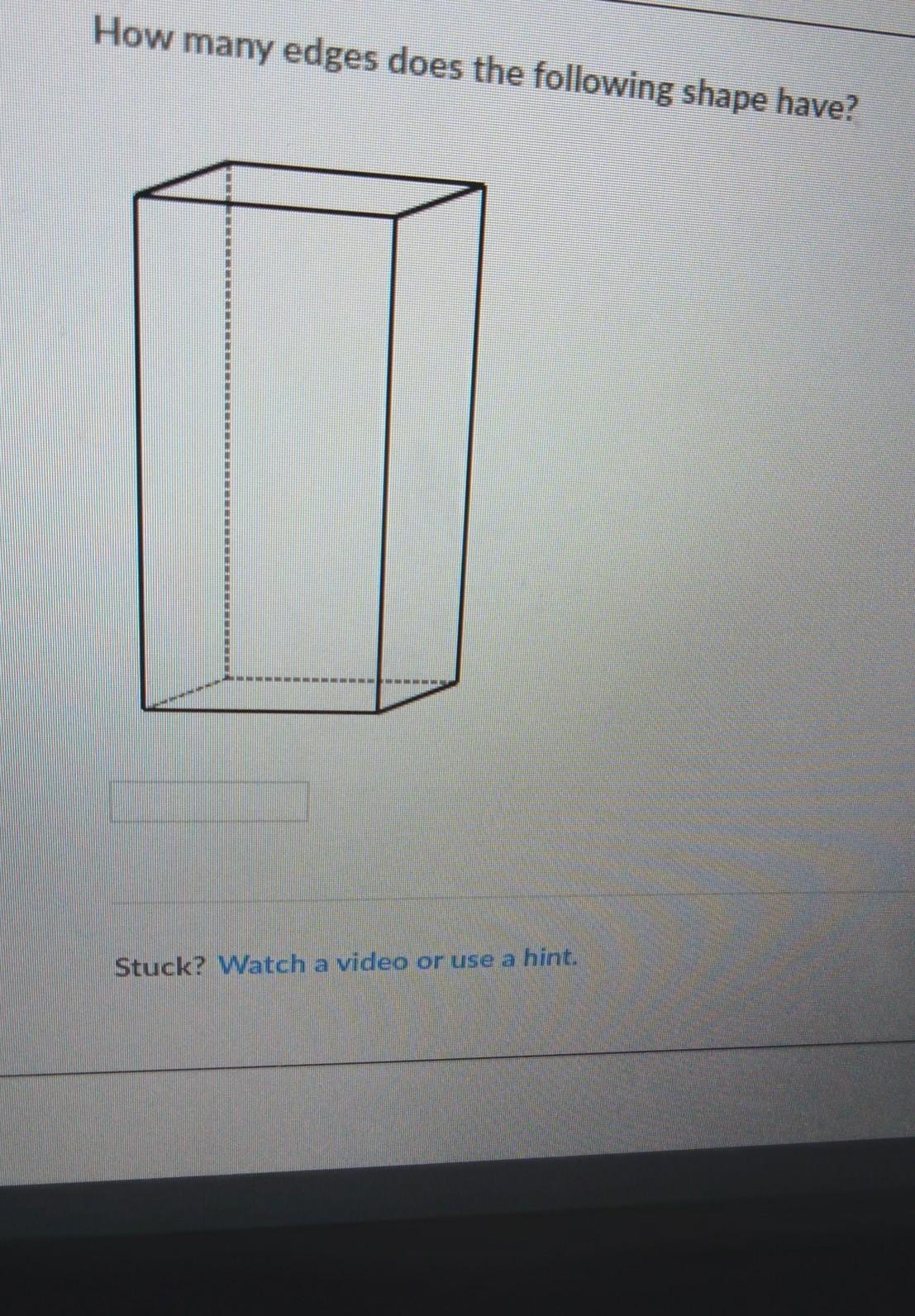
Answers
Answer:
6.
Step-by-step explanation:
Faces in other words is the number of individual shapes on one shape. In this case, how many rectangles is on this shape. Hope this helps have a good day!
Answer:
rectangle is
Edges=12
Faces=6
Vertices=8
[8 Points] Suppose you invest $17,000 into an account that earns 6.75% compounded monthly. a) Find the effective yield rate of the investment. b) How much money will be in the account in 22 years?
Answers
(a) We find that the effective yield rate is approximately 6.91%.
(b) The account will have approximately $70,297.97 in it after 22 years.
a) To find the effective yield rate of the investment, we can use the formula for compound interest:
Effective yield rate = (1 + (annual interest rate / number of compounding periods))^{number of compounding periods - 1}
In this case, the annual interest rate is 6.75% (or 0.0675 as a decimal), and the compounding is done monthly, so the number of compounding periods per year is 12.
Plugging in the values, we get:
Effective yield rate = (1 + (0.0675 / 12))^12 - 1
Calculating this expression, we find that the effective yield rate is approximately 6.91%.
b) To find how much money will be in the account in 22 years, we can use the formula for compound interest:
Future value = Principal * (1 + (annual interest rate / number of compounding periods))^(number of compounding periods * number of years)
In this case, the principal is $17,000, the annual interest rate is 6.75% (or 0.0675 as a decimal), the compounding is done monthly, so the number of compounding periods per year is 12, and the number of years is 22.
Plugging in the values, we get:
Future value = $17,000 * (1 + (0.0675 / 12))^(12 * 22)
Calculating this expression, we find that the future value of the account after 22 years is approximately $70,297.97.
Therefore, the account will have approximately $70,297.97 in it after 22 years.
To learn more about compound interest visit:
brainly.com/question/22621039
#SPJ11
- Evaluate Sc (y + x – 4ix3)dz where c is represented by: C:The straight line from Z = 0 to Z = 1+ i C2: Along the imiginary axis from Z = 0 to Z = i. = =
Answers
The value of the integral C1 and C2 are below:
∫[C1] (y + x – 4ix³) dz = -1/2 + 4/3 i
∫[C2] (y + x – 4ix³) dz = 0
To evaluate the integral, we need to parameterize the given contour C and express it as a function of a single variable. Then we substitute the parameterization into the integrand and evaluate the integral with respect to the parameter.
Let's evaluate the integral along contour C1: the straight line from Z = 0 to Z = 1 + i.
Parameterizing C1:
Let's denote the parameter t, where 0 ≤ t ≤ 1.
We can express the contour C1 as a function of t using the equation of a line:
Z(t) = (1 - t) ×0 + t× (1 + i)
= t + ti, where 0 ≤ t ≤ 1
Now, we'll calculate the differential dz/dt:
dz/dt = 1 + i
Substituting these into the integral:
∫[C1] (y + x – 4ix³) dz = ∫[0 to 1] (Im(Z) + Re(Z) - 4i(Re(Z))³)(dz/dt) dt
= ∫[0 to 1] (t + 0 - 4i(0)³)(1 + i) dt
= ∫[0 to 1] (t + 0)(1 + i) dt
= ∫[0 to 1] (t + ti)(1 + i) dt
= ∫[0 to 1] (t + ti - t + ti²) dt
= ∫[0 to 1] (2ti - t + ti²) dt
= ∫[0 to 1] (-t + 2ti + ti²) dt
Now, let's integrate each term:
∫[0 to 1] -t dt = [-t²/2] [0 to 1] = -1/2
∫[0 to 1] 2ti dt = \(t^{2i}\)[0 to 1] = i
∫[0 to 1] ti² dt = (1/3)\(t^{3i}\) [0 to 1] = (1/3)i
Adding the results together:
∫[C1] (y + x – 4ix³) dz = -1/2 + i + (1/3)i = -1/2 + 4/3 i
Therefore, the value of the integral along contour C1 is -1/2 + 4/3 i.
Let's now evaluate the integral along contour C2: along the imaginary axis from Z = 0 to Z = i.
Parameterizing C2:
Let's denote the parameter t, where 0 ≤ t ≤ 1.
We can express the contour C2 as a function of t using the equation of a line:
Z(t) = (1 - t)× 0 + t × i
= ti, where 0 ≤ t ≤ 1
Now, we'll calculate the differential dz/dt:
dz/dt = i
Substituting these into the integral:
∫[C2] (y + x – 4ix³) dz = ∫[0 to 1] (Im(Z) + Re(Z) - 4i(Re(Z))³)(dz/dt) dt
= ∫[0 to 1] (0 + 0 - 4i(0)³)(i) dt
= ∫[0 to 1] (0)(i) dt
= ∫[0 to 1] 0 dt
= 0
Therefore, the value of the integral along contour C2 is 0.
In summary:
∫[C1] (y + x – 4ix³) dz = -1/2 + 4/3 i
∫[C2] (y + x – 4ix³) dz = 0
Learn more about integral here:
https://brainly.com/question/31059545
#SPJ11
What is the slope of the line that passes theoough the points (1,-6) and (-2,-8)?
Answers
Considering the expression of a line, the slope of the line that passes through the points (1,-6) and (-2,-8) is 2/3.
Equation of a line
A linear equation o line can be expressed in the form y = mx + b
where
x and y are coordinates of a point.m is the slope.b is the ordinate to the origin and represents the coordinate of the point where the line crosses the y axis.Knowing two points (x₁, y₁) and (x₂, y₂) of a line, the slope m of said line can be calculated using the following expression:
m= (y₂ - y₁) ÷ (x₂ - x₁)
Slope in this caseBeing (x₁, y₁)= (1, -6) and (x₂, y₂)= (-2, -8), the slope m can be calculated as:
m= (-8 - (-6)) ÷ (-2 - 1)
m= (-8 +6) ÷ (-2 - 1)
m= (-2) ÷ (-3)
m= 2/3
Finally, the slope in this case is 2/3.
Learn more about the equation of a line having 2 points:
brainly.com/question/12851029
brainly.com/question/19496333
#SPJ1
Sienna has 5 3/4 pounds of grapes. She eats 1/8 pound and gives 2 1/2 pounds to her brother.
How many pounds of grapes does Sienna have left?
Answers
Answer:
3 1/8 lbs left
Step-by-step explanation:
\(5\frac{3}{4} -\frac{1}{8} -2\frac{1}{2}\)
\(\frac{23}{4} -\frac{1}{8} -\frac{5}{2}\)
\(\frac{46}{8} -\frac{1}{8} -\frac{20}{8}\)
\(\frac{46-1-20}{8}\)
\(\frac{25}{8}\) lbs
the data set in ceosal2 contains information on chief executive officers for u.s. corporations. the variable salary is annual compensation, in thousands of dollars, and ceoten is prior number of years as company ceo. find the average salary and the average tenure in the sample. how many ceos are in their first year as ceo (that is, ceoten
Answers
After calculation, the average salary is 865.8644 thousands of dollars and average tenure is 7.955 years. Number of CEOs who are in their first year as CEO is equal to 5.
Here are the steps in R Studio to perform the tasks:
(a) Finding the average salary and the average tenure in the sample:
Load the CEOSAL2 data set in R Studio using the read.csv function.
ceos <- read.csv("CEOSAL2.csv")
Calculate the average salary using the mean function:
average_salary <- mean(ceos$salary)
Calculate the average tenure using the mean function:
average_tenure <- mean(ceos$ceoten)
(b) Finding the number of CEOs in their first year as CEO and the longest tenure as CEO:
Use the sum function and a logical test to count the number of CEOs in their first year as CEO:
first_year_ceos <- sum(ceos$ceoten == 0)
Use the max function to find the longest tenure as CEO:
longest_tenure <- max(ceos$ceoten)
Read more about Average Calculations:
https://brainly.com/question/14371457
#SPJ4
PLEASE HELP!!!!!! It’s algebra

Answers
When the cost of a gallon of milk increases from $2.81 to $3.48 over a period of 10 years the annual inflation rate is 2.15 percent.
What is a annual inflation rate?
A percentage is used to represent the inflation rate. For instance, a yearly inflation rate of 2% indicates that the cost of products and services as a whole has increased by 2%. As an illustration, a product that cost $10 last year will cost $10.20 this year.
Here, we have
Given
The cost of the gallon of milk earlier was $2.81
The cost of a gallon of milk now is $3.48.
The total time period is 10 years.
r = (F/P)ⁿ⁻¹ - 1
r = {(3.48/2.81)^(1/10) - 1}×100
r = {(1.238)^(1/10) - 1}×100
r = 0.0215 ×100
r = 2.15
Hence, when the cost of a gallon of milk increases from $2.81 to $3.48 over a period of 10 years the annual inflation rate is 2.15 percent.
To learn more about the annual inflation rate from the given link
https://brainly.com/question/24723238
#SPJ1
Find the value of the expression: 9 / 3 + ( 5 - 3 )^2
Answers
Answer:
u arrange it mathematically and then you'll be able to get the answer

Indeterminate form [0^0]: Calculate the following limits using L'Hospital's Rule.
lim tanx^sinx
x-> 0+
With the way the problem is written on my homework, I'm not sure if it's (tanx)^sinx or tan(x^sinx). Answers to both methods would be helpful.
Answers
When interpreting the expression as \((tanx)^{(sinx)\), the limit using L'Hospital's Rule is -∞ as x approaches 0+. However, when interpreting the expression as\(tan(x^{sinx})\), the limit is not well-defined due to the indeterminate form of 0^0.
To calculate the limit using L'Hospital's Rule, let's consider both interpretations of the expression and find the limits for each case:
Case 1: lim\((tanx)^{(sinx)\) as x approaches 0+
Taking the natural logarithm of the expression, we have:
\(ln[(tanx)^{(sinx)}] = sinx * ln(tanx)\)
Now, we can rewrite the expression as:
\(lim [sinx * ln(tanx)]\)as x approaches 0+
Applying L'Hospital's Rule, we differentiate the numerator and denominator:
\(lim [(cosx * ln(tanx)) + (sinx * sec^{2}(x))] / (1 / tanx)\) as x approaches 0+
Simplifying the expression:
\(lim [cosx * ln(tanx) + sinx * sec^{2}(x)] * tanx\) as x approaches 0+
\(lim [cosx * ln(tanx) + sinx * sec^{2}(x)] * (sinx / cosx)\) as x approaches 0+
\(lim [(cosx * ln(tanx) + sinx * sec^{2}(x)) / cosx] * sinx\) as x approaches 0+
\(lim [ln(tanx) + (sinx / cosx) * sec^{2}(x)] * sinx\) as x approaches 0+
\(lim [ln(tanx) + tanx * sec^{2}(x)] * sinx\) as x approaches 0+
Since lim ln(tanx) as x approaches 0+ = -∞ and\(lim (tanx * sec^{2}(x))\) as x approaches 0+ = 0, we have:
\(lim [ln(tanx) + tanx * sec^{2}(x)] * sinx\) as x approaches 0+ = -∞
Therefore, the limit of \((tanx)^{(sinx)\) as x approaches 0+ using L'Hospital's Rule is -∞.
Case 2: lim\(tan(x^{sinx})\)as x approaches 0+
We can rewrite the expression as:
lim\(tan(x^{(sinx)})\) as x approaches 0+
This expression does not have an indeterminate form of \(0^0\), so we do not need to use L'Hospital's Rule. Instead, we can substitute x = 0 directly into the expression:
lim \(tan(0^{(sin0)})\) as x approaches 0+
lim\(tan(0^0)\)as x approaches 0+
The value of \(0^0\) is considered an indeterminate form, so we cannot determine its value directly. The limit in this case is not well-defined.
For more question on L'Hospital's Rule visit:
https://brainly.com/question/24116045
#SPJ8
Suppose you are testing the hypotheses H0: π = 0.25 and Ha: π < 0.25 and the observed statistic, pˆ is equal to 0.30 with a sample size of 100.
a. If you are using a proportion as your statistic, where do you expect your null distribution to be centered?
b. If you are using a count as your statistic, where do you expect your null distribution to be centered
Answers
a. Null distribution is expected to be centered at the hypothesized proportion, which is 0.25.
b. Null distribution is expected to be centered at 25.
a. If you are using a proportion as your statistic, you expect the null distribution to be centered at the hypothesized proportion, which is 0.25 in this case.
b. If you are using a count as your statistic, you expect the null distribution to be centered at the expected count, which is np under the null hypothesis, where n is the sample size and p is the hypothesized proportion. In this case, np = 100 * 0.25 = 25.
To know more about null hypothesis click here:
https://brainly.com/question/11614388
#SPJ11
how many multiples of $9^3$ are greater than $9^4$ and less than $9^5$?
Answers
There are 72 multiples of 9³ that are greater than \(9^4\) and less than \(9^5\).
We have,
The values of 9³, \(9^4\), and \(9^5\):
9³ = 729
\(9^4\) = 6561
\(9^5\) = 59049
Now,
The multiples of 729 that fall within the range (6561, 59049).
The number of multiples can be calculated as follows:
Multiples = (Highest value ÷ Divisor) - (Lowest value ÷ Divisor)
= (59049 ÷ 729) - (6561 ÷ 729)
= 81 - 9
= 72
Therefore,
There are 72 multiples of 9³ that are greater than \(9^4\) and less than \(9^5\).
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ12
Given the triangle ABC, what is the measure of angle B?
38.612
81.853
6.214
64.147

Answers
Answer:
\(64.147^{\circ}\)
Step-by-step explanation:
The explanation is attached below.

Select all that apply

Answers
Answer and Step-by-step explanation:
The numbers that are irrational are the square root of 27 and the square root of 55. ( \(\sqrt{27}, \sqrt{55}\) ).
This is because those numbers don't have a perfect square root.
The square root of 16 and the square root of 64 have perfect square roots (16 having the answer as 4, and 64 having the answer as 8).
#teamtrees #PAW (Plant And Water)
Help please! Giving brainliest! Determine weather x and y show direct variation. If so, identify the constant of variation.
y=3x+2
Answers
Answer:
not direct variation
Step-by-step explanation:
You want to know if the equation y = 3x +2 represents a direct variation between x and y.
Direct variationDirect variation is characterized by the equation ...
y = kx
for a constant of variation k. The point (0, 0) is on a graph of direct variation.
Given equationThe given equation is not in this form, and cannot be put in this form. The value of y when x=0 is not 0, so the variation is not direct.
<95141404393>
How do you know it two line segments are parallel? A. The slope of one is the negative of the slope of the other B. Their slopes are negative reciprcals C. Their slopes are equal D. Their slopes are reciprocals
Answers
Answer: 1 2 imm comingg for youuuuuuuuuuuuu
Step-by-step explanation:
Answer:
C. their slope are equal
Step-by-step explanation:
Ex: Solve by reduction of order: 1) y ′′
+16y=0 given y 1
=cos4x
Answers
The general solution to the differential equation y'' + 16y = 0 is y(x) = (c₁ + c₂) * cos(4x)
To solve the differential equation y'' + 16y = 0 using reduction of order, we'll assume a second solution of the form y₂(x) = u(x) * y₁(x), where y₁(x) is a known solution and u(x) is an unknown function.
Given y₁(x) = cos(4x), we'll differentiate it to find y₁'(x) and y₁''(x):
y₁'(x) = -4sin(4x)
y₁''(x) = -16cos(4x)
Now we substitute y₂(x) = u(x) * y₁(x) into the original differential equation:
y'' + 16y = 0
(-16cos(4x)) + 16(u(x) * cos(4x)) = 0
Simplifying the equation:
-16cos(4x) + 16u(x) * cos(4x) = 0
cos(4x)(-16 + 16u(x)) = 0
For this equation to hold for all values of x, we must have (-16 + 16u(x)) = 0.
Solving for u(x):
-16 + 16u(x) = 0
16u(x) = 16
u(x) = 1
Now we have the second solution:
y₂(x) = u(x) * y₁(x)
y₂(x) = 1 * cos(4x)
y₂(x) = cos(4x)
Therefore, the general solution to the differential equation y'' + 16y = 0 is:
y(x) = c₁ * y₁(x) + c₂ * y₂(x)
y(x) = c₁ * cos(4x) + c₂ * cos(4x)
y(x) = (c₁ + c₂) * cos(4x)
Where c₁ and c₂ are arbitrary constants.
Learn more about reduction of order at
https://brainly.com/question/32250420
#SPJ11
Gribbles are small, pale white, marine worms that bore through wood. While sometimes considered a pest since they can wreck wooden docks and piers, they are now being studied to determine whether the enzyme they secrete will allow us to turn inedible wood and plant waste into biofuel.1 A sample of 50 gribbles finds an average length of 3.1 mm with a standard deviation of 0.72. Give a best estimate for the length of gribbles, a margin of error for this estimate (with 99% confidence), and a 99% confidence interval. Round your answer for the point estimate to one decimal place, and your answers for the margin of error and the confidence interval to two decimal places. point estimate = Enter your answer; point estimate margin of error = Enter your answer; margin of error The 99% confidence interval is Enter your answer; The 99%confidence interval, value 1 to Enter your answer; The 99%confidence interval, value 2
Answers
Answer:
a) The Margin of Error = 0.26
b) The 99% Confidence Interval = ( 2.84, 3.36)
Step-by-step explanation:
a) Margin of Error
The formula for Margin of Error =
z × Standard deviation/√n
From the above question
The z score for 99% confidence interval = 2.576
Standard deviation = 0.72
n = Random number of samples = 50
Margin of Error =
2.576 × 0.72/√50
= 1.85472 /√(50)
= 0.2622970178
Approximately to 2 decimal places = 0.26
b) 99% Confidence Interval
= Mean ± Margin of Error
Mean = 3.1mm
Confidence Interval = 3.1 ± 0.26
3.1 ± 0.26
= 2.84
3.1 + 0.26
= 3.36
The 99% Confidence Interval = ( 2.84, 3.36)
Helen wanted to add some rosebushes and hostas to her garden. Her first purchase was 8 rosebushes and 4 hostas for a total of $140. Helen realized she had room for more plants so the next day she bought 4 more rosebushes and 3 more hostas and spent $80. How much did she spend on each rosebush?
Answers
The cost of each rosebush is $12.5. Her first purchase was 8 rosebushes and 4 hostas for a total of $140.
Let's assume the cost of each rosebush is represented by "r" (in dollars), and the cost of each hosta is represented by "h" (in dollars).
From the given information, we can create a system of equations:
Equation 1: 8r + 4h = 140 (total cost of 8 rosebushes and 4 hostas)
Equation 2: 4r + 3h = 80 (total cost of 4 additional rosebushes and 3 additional hostas)
To solve this system, we can use the method of elimination. Multiply Equation 1 by 3 and Equation 2 by 4 to eliminate the "h" term:
Equation 1: 24r + 12h = 420
Equation 2: 16r + 12h = 320
Subtract Equation 2 from Equation 1:
(24r + 12h) - (16r + 12h) = 420 - 320
8r = 100
Divide both sides by 8:
r = 100 / 8
r = 12.5
Therefore, the cost of each rosebush is $12.5.
Learn more about cost here
https://brainly.com/question/2292799
#SPJ11
solve for x and y then find angle ABE

Answers
Answer: x is 9° , y is 21°. The measure of angle ABE is 48°.
Step-by-step explanation:
First we will solve for x.
The variable x appears in the angle 8x + 18 and that angle is a right angle.
Right angles have the measure of 90 degrees so we will set the angle equal 90 and solve for x.
8x + 18 = 90 Subtract 18 from both sides
- 18 -18
8x = 72 divide both sides by 8
x = 9
y is also on the right side and the combination of both angles has to also equal 90 degrees because they form a right angle.
Since we already know x is 9 we will input it into the left side for x and solve for y.
y + 3(9) + 2y = 90
3y + 27= 90
-27 -27
3y = 63
y = 21
Now we need to find the measure of angle ABE.
ABE is represented by y + 3x so since we know the value of y and x we will input it into the expression and solve for the angle.
21 + 3(9) = m∠ABE
21 + 27= m∠ABE
48 = m∠ABE
This means the measure of angle ABE is 48°
Write the explicit formula for the sequence:

Answers
The explicit rule for the sequence is f(n) = 6 - 4(n - 1)
Finding the explicit rule for the sequenceFrom the question, we have the following parameters that can be used in our computation:
a1 = 6
a(n) = a(n - 1) - 4
In the above sequence, we can see that -4 is added to the previous term to get the new term
This means that
First term, a = 6
Common difference, d = -4
The nth term is then represented as
f(n) = a + (n - 1) * d
Substitute the known values in the above equation, so, we have the following representation
f(n) = 6 - 4(n - 1)
Hence, the explicit rule isf(n) = 6 - 4(n - 1)
Read more about sequence at
brainly.com/question/30499691
#SPJ1
Spray drift is a constant concern for pesticide applicators and agricultural producers. The inverse relationship between droplet size and drift potential is well known. The paper "Effects of 2,4-D Formulation and Quinclorac on Spray Droplet Size and Deposition" investigated the effects of herbicide formulation on spray atomization. A figure in the paper suggested the normal distribution with mean 1050 μm and variance 22500 μm was a reasonable model for droplet size for water (the control treatment) sprayed through a 760 ml/min nozzle.
a. What is the probability that the size of a single droplet is less than 1500 μm? At least 1000μm?
b. What is the probability that the size of a single droplet is between 1000 and 1500 μm?
c. How would you characterize the smallest 2% of all droplets?
d. If the sizes of five independently selected droplets are measured, what is the probability that
at least one exceeds 1500 μm?
Answers
To answer the questions related to the probability of droplet sizes, we'll use the normal distribution with the given mean and variance. Let's solve each part of the question:
a. Probability that the size of a single droplet is less than 1500 μm:
To find this probability, we need to calculate the cumulative distribution function (CDF) of the normal distribution up to 1500 μm. We'll use the z-score formula:
z = (x - μ) / σ
Where:
x = droplet size (1500 μm)
μ = mean (1050 μm)
σ = standard deviation (square root of the variance, which is sqrt(22500 μm))
Calculating the z-score:
z = (1500 - 1050) / sqrt(22500)
= 450 / 150
= 3
Using the z-score table or a calculator, we can find that the cumulative probability corresponding to z = 3 is approximately 0.9987.
Therefore, the probability that the size of a single droplet is less than 1500 μm is approximately 0.9987.
b. Probability that the size of a single droplet is between 1000 and 1500 μm:
Similar to part (a), we need to calculate the cumulative probability for two values: 1000 μm and 1500 μm. Let's calculate the z-scores for both values:
For 1000 μm:
z_1000 = (1000 - 1050) / sqrt(22500)
For 1500 μm:
z_1500 = (1500 - 1050) / sqrt(22500)
Once we have the z-scores, we can find the corresponding cumulative probabilities using the z-score table or a calculator. Then, we subtract the probability for 1000 μm from the probability for 1500 μm to find the probability between the two values.
c. Characterizing the smallest 2% of all droplets:
To characterize the smallest 2% of droplets, we need to find the droplet size that corresponds to the 2nd percentile of the normal distribution. In other words, we need to find the value x such that the cumulative probability up to x is 0.02. We can use the z-score formula to solve for x:
z = (x - μ) / σ
We'll find the z-score corresponding to the cumulative probability 0.02 using the z-score table or a calculator. Then, we can rearrange the formula to solve for x:
x = z * σ + μ
d. Probability that at least one of five independently selected droplets exceeds 1500 μm:
To find this probability, we'll use the complement rule. The probability that none of the five droplets exceed 1500 μm is the complement of the probability that at least one of them exceeds 1500 μm. We can calculate this probability by subtracting the probability of none from 1. We'll use the probability obtained in part (a) for a single droplet.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
Which statement is true about the sum of two rational numbers? It can always be written as a fraction. It can never be written as a fraction. It can always be written as a repeating decimal. It can never be written a terminating decimal. ?
Answers
Answer:
It can always be written as a fraction.
Step-by-step explanation:
The importance of this question is to differentiate rational and irrational numbers.
Rational numbers can be written as a ratio, hence a fraction, or a repeating or terminating decimal.
Irrational numbers cannot be written as a ratio and will not have a terminating or repeating decimal.
So the first statement is true since the sum of two rational numbers will be rational.
The second statement is false since the sum of two rational numbers can absolutely be represented by a fractional ratio.
The third statement is false since the sum of two rational numbers is not always a repeating decimal.
The fourth statement is false since the sum of two rational numbers could be written as a terminating decimal.
Cheers.
I agree with the other person's response. The sum is always rational (it can always be written as a fraction of integers)
----------------
Here's a proof:
Let x and y be two rational numbers. This means
x = a/b
y = c/d
where a,b,c,d are integers. The denominators b and d cannot be 0.
----------------
Let's add x and y, then simplify
x+y = (a/b) + (c/d)
x+y = (ad/bd) + (bc/bd)
x+y = (ad+bc)/(bd)
This last expression is in the form p/q
p = ad+bc is an integer
q = bd is also an integer
we have a ratio or fraction of integers, therefore x+y is also rational
D is 13. What is the length of the line.

Answers
Answer:
D
Step-by-step explanation:
You have to use pythagorean theorem to solve this.
Answer:
D
Step-by-step explanation:
use pytherogream theory
sides, 5 and 12
pytherogream triple 5, 12, 13
Mr. Smiths algebra class is inquiring about slopes of lines. The class was asked to graph the total cost, c, of buying h hotdog that cost 75 cent each. The class was asked to describe the slope between any two points on the graph. Which statement below is always a correct answer about the slope between any two points on this graph?
1)the same positive value
2)the same negative value
3) zero
4) a positive value, but the values vary
Answers
The slope of the graph is the same positive value that is 0.75.
Hence the correct option is (1).
We know that the equation of a straight line with slope 'm' and y intercept 'c' is given by,
y = mx + c
Here the model equation
c = 0.75h, where c is the total cost to buy hotdogs
h is the number of hotdogs bought
And 0.75 is the price of one hotdog
Now we can clearly say that c = 0.75h will make a straight line coordinate plane.
Now comparing the equation with slope intercept equation of straight line we get,
m = 0.75 and c = 0
So the slope of the line represented by model equation = 0.75 which is a positive number.
y intercept = 0.
We know that the slope of one particular straight line on cartesian plane is unique.
So, the slope of the graph is the same positive value.
Hence the correct option is (1).
To know more about slope here
https://brainly.com/question/3493733
#SPJ1
plese help me i need it

Answers
Answer:
B
Step-by-step explanation:
0.25=1/4=15/60
3/20=9/60
20%=1/5=12/60
1/3=20/60
Now we can easily put them in order since they have a common denominator.
9<12<15<20
Now let's bring back the original numbers in the same order as shown above.
3/20, 20%, 0.25, 1/3
Choice B matches this order.
Find a linear regression model for the weekly cost data, using z as the independent variable. C(z) = ma +k Round m to 1 decimal place, and round k to the nearest integer. Use the weekly cost model to estimate the total weekly cost when the weekly demand is 210. Round to the nearest dollar $_____. What is the per unit variable cost? Round to 1 decimal place. $_____. per sleeping bag What is the weekly fixed cost of producing sleeping bags? Round to the nearest integer $_____.
Answers
The linear regression model for the weekly cost data is given by C(z) = ma + k, where z is the independent variable representing the weekly demand.
The values of m and k are determined through the regression analysis. Using this model, we can estimate the total weekly cost for a given weekly demand and calculate the per unit variable cost and weekly fixed cost.To find the linear regression model, we need to perform a regression analysis on the given weekly cost data. This analysis will determine the values of m and k in the equation C(z) = ma + k, where C(z) represents the weekly cost and z represents the weekly demand.
Once the values of m and k are obtained, we can use the model to estimate the total weekly cost when the weekly demand is 210. By plugging in z = 210 into the equation C(z) = ma + k, we can calculate the total weekly cost rounded to the nearest dollar.The per unit variable cost can be determined by the value of m in the model. It represents the change in cost per unit change in demand. By rounding m to one decimal place, we can obtain the per unit variable cost rounded to one decimal place.
The weekly fixed cost can be determined by the value of k in the model. It represents the cost that does not depend on the weekly demand. By rounding k to the nearest integer, we can obtain the weekly fixed cost rounded to the nearest dollar.Overall, by applying the linear regression model to the given data, we can estimate the total weekly cost, calculate the per unit variable cost, and determine the weekly fixed cost of producing sleeping bags.
Learn more about linear regression model here: brainly.com/question/30470285
#SPJ11
If X = 3t4 + 7 and y = 2t - t2, find the following derivatives as functions of t. dy/dx = d^2y/dx^2 =
Answers
The derivative function is dy/dx = (1 - t) / (\(6t^3\)) and \(d^2y/dx^2\) = \((-1 / (6t^3))\)- (3 / \((2t^4)\)
To find dy/dx, we need to differentiate y with respect to t and x with respect to t, and then divide the two derivatives.
Given:
\(x = 3t^4 + 7\)
\(y = 2t - t^2\)
Differentiating y with respect to t:
dy/dt = 2 - 2t
Differentiating x with respect to t:
\(dx/dt = 12t^3\)
Now, to find dy/dx, we divide dy/dt by dx/dt:
\(dy/dx = (2 - 2t) / (12t^3)\)
To simplify this expression further, we can divide both the numerator and denominator by 2:
\(dy/dx = (1 - t) / (6t^3)\)
The second derivative \(d^2y/dx^2\)represents the rate of change of the derivative dy/dx with respect to x. To find \(d^2y/dx^2\), we differentiate dy/dx with respect to t and then divide by dx/dt.
Differentiating dy/dx with respect to t:
\(d^2y/dx^2 = d/dt((1 - t) / (6t^3))\)
To simplify further, we can expand the differentiation:
\(d^2y/dx^2 = (-1 / (6t^3)) - (3 / (2t^4))\)
learn more about differentiation here:
https://brainly.com/question/24062595
#SPJ11