tropical storm jayton moved 87/100 miles in 1/20 hour. how far did the storm move in 1 hour
Answers
The tropical storm jayton covered 87/5 miles in 1 hour.
We are given;
Tropical storm jayton moved 87/100 miles in 1/20 hour.
We will solve the given problem using the unitary method.
Since the tropical storm jayton in 1/20 hour moved 87/100 miles.
So, the tropical storm jayton in 1 hour moved (87/100)/(1/20) miles
= 87/100 * 20 miles
= 87/5 miles
Thus, the tropical storm jayton covered 87/5 miles in 1 hour.
We can also use the direct proportional method for the given problem;
Let tropical storm jayton cover x miles in 1 hour.
1/20 : 1 :: 87/100 : x
1/20 = 87/100x
x = 87/100 * 20
x = 87/5 miles
Thus, the tropical storm jayton covered 87/5 miles in 1 hour.
To learn more about the unitary method visit:
https://brainly.com/question/21648365
#SPJ9
Related Questions
(b) An Investment is estimated to grow at the rate al 15% per annum. If the worth of the Investment now is ¢850,000 i. What will its worth be in the 6th year? What is the percentage increase in its worth after 6th year? In what year will the investment worth ¢3.23million ?
Answers
Answer:
~9.6 years it will be worth 3.23 mil.
Step-by-step explanation:
This problem requires use of the growth formula.
PART 1:
Equation:
\(3,230,000 = 850,000 * (1.15)^6\)
By solving this you get:
A valuation of $1,966,101.65078125 after 6 years
PART 2:
Equation:
\(3,230,000 = 850,000*(1+.15)^x\)
By solving this (which im too lazy to show the steps for) you get:
x = years
x = ~9.6 years / 9.55196417 years
QuestionFind the equation of the line with slope m=1/4 that contains the point (4,5)
Answers
The standard form equation for a line is
\(y=mx+b\)in which m represents the slope and b the y-intercept.
start putting the value of the slope into the equation
\(y=\frac{1}{4}x+b\)although it is a fraction we repace it as if it was a whole number
then using (4,5) as (x,y) we can find b, the y-intercept
\(5=\frac{1}{4}(4)+b\)simplify both sides of the equation
\(5=1+b\)subtract 1 one on both sides in order to find b
\(\begin{gathered} 5-1=1+b-1 \\ 4=b \\ b=4 \end{gathered}\)The equation of the line is
\(y=\frac{1}{4}x+4\)Maria's grandmother gave her a gift of $2,000 for her birthday in November 2015. She deposited this into a savings account on January 2, 2016, after the holidays. The savings bank offered 0.725% interest at the time. Over the next year, the inflation rate averaged 1.3%. Now consider the following statements:
Statement I: In 2016, the buying power of Maria's gift decreased by about 0.6%.
Statement II: Maria's gift earned around $14.50 in interest during 2016, but this amount did not keep up with inflation.
Statement III: Maria's savings account had less than $2000 in it by the end of 2016.
Statements I and II are correct, but not Statement III.
None of the statements are correct.
All the statements are correct.
Statements I and III are correct, but not Statements II.
Statements II and III are correct, but not Statements I.
Answers
According to the given question we can conclude that statement I and statement II are correct but not statement III.
Define interest?Interest is the cost incurred when lending and borrowing a specific amount of money from a financial standpoint. It is crucial to note that interest is calculated as a percentage.
given,
Statement I is correct because the inflation rate averaged 1.3%, and Maria's savings account earned interest at a rate of 0.725%, which is lower than the inflation rate. This means that the buying power of her gift decreased by approximately 1.3% - 0.725% = 0.575% or 0.6% (rounded).
Statement II is also correct because Maria's savings account earned interest on the deposit of $2,000 for one year at a rate of 0.725%. The interest earned can be calculated as:
Interest = Principal x Rate x Time
Interest = $2,000 x 0.00725 x 1 year
Interest = $14.50
However, statement III is not correct. Since Maria deposited the entire gift of $2,000 into the savings account and did not make any withdrawals during the year, the balance in the account at the end of 2016 would be the sum of the initial deposit and the interest earned, which is $2,000 + $14.50 = $2,014.50. Therefore, the correct option is:
Statement III is incorrect, however Statements I as well as II are true.
To know more about interest visit:
https://brainly.com/question/28960137
#SPJ1
I need help please
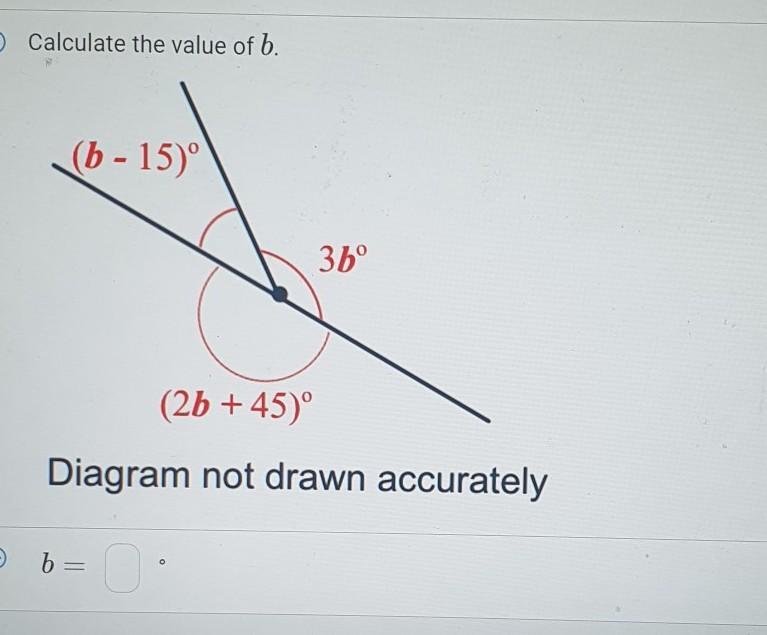
Answers
Answer:
b = 55°
Step-by-step explanation:
Angles around a point will always add up to 360°
Therefore, we can write an expression where we sum the 3 angles given and equate them to 360°:
(b - 15) + 3b + (2b + 45) = 360
eliminate the brackets and collect like terms:
b + 3b + 2b - 15 + 45 = 360
Combine like terms:
6b + 30 = 360
subtract 30 from both sides:
6b = 330
divide both sides by 6:
6b ÷ 6 = 330 ÷ 6
⇒ b = 55
A national study, that revealed a normal distribution, revealed that the average time a student spends studying statistics on a weekend is 60 minutes. A random sample of 11 students in BU 203 were asked to record their statistic study time over a weekend. The sample revealed an average study time of 44.27 minutes with a standard deviation of 20.4. With an alpha of 5% State the null hypothesis (H0) and the alternate hypothesis (H1). Draw the distribution.
Answers
Answer:
Null hypothesis = H0 : μ = 60
Alternative hypothesis = H1 : μ < 60
Step-by-step explanation:
From the question given :
μ = 60 minutes
xbar = 44.27 minutes
s = 20.4 minutes
The alternative hypothesis is the claim ; which is to hypothesize that the average studying time is 44.27 (which is less than the population average studying time)
The null hypothesis is the initial truth and it is the opposite of the alternative hypothesis.
The hypothesis are :
H0 : μ = 60
H1 : μ < 60
Given triangle GHJ, the measure of angle G equals 110°, the measure of angle J equals 40°, and the measure of angle H equals 30°. Complete the following statements. Since angle G is angle, the opposite side, JH, is . The order of the side lengths from longest to shortest is .
Answers
Answer:
Since angle G is
✔ the largest
angle, the opposite side, JH, is
✔ the longest side
. The order of the side lengths from longest to shortest is
✔ HJ, GH, and GJ
.
Step-by-step explanation:
Answer: the answers are
-the largest
-the longest side
-HJ, GH, and GJ
Step-by-step explanation: put them in edge 2020, got them right Hope this helps :)
Help, this is my math hw and I don't get it!
Pictures are attached below...
I need to show my work too, so i need a file to your work!
I'll mark brainliest if you can answer it.


Answers
So 3x KLM = 72 deg.
KLM = 72 / 3 = 24 deg
MLN = 2x KLM = 24 x 2 = 48 deg.
Consider the function f,g:\(\mathbb{R} \to\mathbb{R}\) defined by
\( \rm f(x) = {x}^{2} + \frac{5}{12} \: and \: g(x) = \begin{cases}2 \bigg( \rm 1 - \dfrac{4 |x| }{3} \bigg), \: \: \: \: |x| \leq \dfrac{3}{4}, \\ \\ 0, \: \: \: \: \: \rm \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: |x| > \dfrac{3}{4} .\end{cases} \)
If \(\alpha\) is the area of the region
\( \rm \bigg \{(x,y) \in \mathbb{R} \times \mathbb R : |x| \leq \dfrac{3}{4} ,0 \leq y \leq min \{f(x),g(x) \} \bigg \}\)
then the value of 9\(\alpha\)
Answers
Suppose \(x>0\); then the curves meet when
\(x^2 + \dfrac5{12} = 2 - \dfrac83 x \implies x^2 + \dfrac83 x - \dfrac{19}{12} = \left(x + \dfrac{19}6\right) \left(x - \dfrac12\right) = 0 \\\\ \implies x = \dfrac12\)
By symmetry, they intersect at \(x=\pm\frac12\).
We also see that \(\min\left\{f(x):|x|\le\frac34\right\} = \frac5{12}\) and \(\max\left\{g(x):|x|\le\frac34\right\} = 2\) at \(x=0\). \(f\) and \(g\) are continuous, so it follows that
\(\min\left\{f(x),g(x) :|x|\le\frac34\right\} = \begin{cases} f(x) & \text{if } |x| < \frac12 \\ g(x) & \text{if } |x| > \frac12 \\ f\left(\pm\frac12\right) = g\left(\pm\frac12\right) = \frac23 & \text{if } x = \pm\frac12 \end{cases}\)
Compute the area \(\alpha\). Taking advantage of symmetry again, we have
\(\alpha = \displaystyle 2 \int_0^{1/2} \int_0^{f(x)} dy\,dx + 2 \int_{1/2}^{3/4} \int_0^{g(x)} dy \, dx \\\\ ~~~~ = 2 \int_0^{1/2} f(x) \, dx + 2 \int_{1/2}^{3/4} g(x) \, dx \\\\ ~~~~ = \left. 2 \left(\frac{x^3}3 + \frac{5x}{12}\right) \right\vert_0^{1/2} + \left. 2 \left(2x - \frac{8x^2}6\right) \right\vert_{1/2}^{3/4} \\\\ ~~~~ = \left(\frac12 - 0\right) + \left(\frac32 - \frac43\right) = \frac23\)
and it follows that \(9\alpha = \boxed{6}\).
solve the system of equations y=3x y=x^2-18
Answers
Answer:
Point Form:
(6,18), (-3,-9)
Equation Form:
x=6, y=18
x=-3, y=-9
Step-by-step explanation:
Solve for the first variable in the first equation, then substitute the result into the other equation.
Answer:
x=-3 , x=6
so
y=-9 or y=18
is y=2x or y=-4x bigger one
Answers
Answer:
Explanation:
Given the expressions y = 2x and y = -4x, we need to know the greatest one.
From both equations, we can see that the variable y is directly proportional to x as shown:
y α x
y = kx
k is the constant of proportionality
First, we need to get the constant of proportionality for both equations. The greater the constant of proportionality, the greater the equation.
For the equation y = 2x
kx = 2x
k = 2
For the equation y = -4x
kx = -4x
k = -4
Since 2 is greater than -4, this shows that the equation y = 2x is greater.
Industrial Designs has been awarded a contract to design a label for a new wine produced by Lake View Winery. The company estimates that 150 hours will be required to complete the project. The firm’s three graphic designers available for assignment to this project are Lisa, a senior designer and team leader; David, a senior designer; and Sarah, a junior designer. Because Lisa has worked on several projects for Lake View Winery, management specified that Lisa must be assigned at least 40% of the total number of hours assigned to the two senior designers. To provide label designing experience for Sarah, the junior designer must be assigned at least 15% of the total project time. However, the number of hours assigned to Sarah must not exceed 25% of the total number of hours assigned to the two senior designers. Due to other project commitments, Lisa has a maximum of 50 hours available to work on this project. Hourly wage rates are $30 for Lisa, $15 for David, and $18 for Sarah.Formulate a linear program that can be used to determine the number of hours each graphic designer should be assigned to the project to minimize total cost (in dollars). (Assume L is the number of hours Lisa is assigned to the project, D is the number of hours David is assigned to the project, and S is the number of hours Sarah is assigned to the project.)
Answers
Answer:
a) Minimize Z =30 X1 +25 X2+18 X3
subject to following constraints
\(1.X1\geq 0.4\left ( X1+X2 \right )\\2.X3\geq 0.15\left ( X1+X2+X3 \right )\\3.X1+X2+X3\leq 150\\4.X3\geq 0.25\left ( X1+X2 \right )\\5.X1\leq 50\\6.X1,X2,X3\geq 0\)
b) Total cost=\(30 \times 48+15\times72+18\times30\) = $3180.
c) As the dual price for constraint five is zero hence additional work hours for Lisa won't change the optimum solution.
Step-by-step explanation:
Step 1:-
a)
Let's take
X1 to be the number of hours assigned to Lisa
X2 to be the number of hours assigned to David
X3 to be the number of hours assigned to Sarah.
The objective function is to attenuate the entire cost of the project by deciding an optimum number of hours for every person. the target function is given by -
Minimize Z =30 X1 +25 X2+18 X3
subject to following constraints
\(1.X1\geq 0.4\left ( X1+X2 \right )\\2.X3\geq 0.15\left ( X1+X2+X3 \right )\\3.X1+X2+X3\leq 150\\4.X3\geq 0.25\left ( X1+X2 \right )\\5.X1\leq 50\\6.X1,X2,X3\geq 0\)
Constraints and explanation:
1. Lisa must be assigned a minimum of 40% of the entire number of hours assigned to the 2 senior designers.
2. Sarah must be assigned a minimum of 15% of the entire project time.
3. The corporate estimates that 150 hours are going to be required to finish the project.
4. The number of hours assigned to Sarah must not exceed 25% of the entire number of hours assigned to the 2 senior designers.
5. Lisa features a maximum of fifty hours available to figure on this project.
6. Non-negative condition.
Step 2:-
b)
From the above equations, we get
The number of hours assigned to Lisa is 48 hours
The number of hours assigned to David 72 hours
The number of hours assigned to Sarah 30 hours.
Total cost=\(30 \times 48+15\times72+18\times30\) = $3180.
Step 3:-
c)
As the dual price for constraint five is zero hence additional work hours for Lisa won't change the optimum solution.
) 65 people were asked on the activities they engage in during their free time. The results showed that 23 visit national parks, 26 engage in cycling while 22 engage in swimming. Furthermore 9 engage in swimming and visit national parks, 9 engage in swimming only while 11 visit national parks only. How many engage in
i. Swimming and cycling
Answers
Answer:
Step-by-step explanation:
i am working on the assumption that nobody does all three of them
i got 4 because including the people that do swimming and park, the total number of people that do swimming is 22.
the same logic goes for cycling: including the people that do swimming and visit the national park, the total is 23.
so that means that find how many people do swimming and cycling, we have to add the people doing only swimming, with the people doing both swimming and park and then subtract that answer from 22 which gives you 4

What is the slope of the line that contains these points?
x
39 40 41
42
y
36
29 22 15
Answers
Answer:
-7
Step-by-step explanation:
The slope of the line between two points can be found using the slope formula:
m = (y2 -y1)/(x2 -x1)
__
Using the first two points from your list, we find the slope to be ...
m = (29 -36)/(40-39) = -7/1 = -7
The slope of the line is -7.
Magnolia, Inc., manufactures bedding sets. The budgeted production is for 15,100 comforters this year. Each comforter requires 7 yards of material. The estimated January 1 beginning inventory is 5,650 yards with the desired ending balance of 5,500 yards of material. If the material costs $5.80 per yard, determine the materials budget for the year.
Answers
As a result, the annual materials budget is $611,540.
What is the budget for materials?The process of creating a material or buy budget that includes the amount and financial value of the materials to be purchased within a given time frame is known as material budgeting. Further to analysing the material requirements, it assists in estimating material prices over time.
To start, we must determine how much material will be needed to make 15,100 comforters:
15,100 comforters multiplied by their 7 yards of fabric each equal 105,700 yards of material.
The amount of material that must be purchased must then be determined:
Desired ending inventory + Material required for production - Beginning inventory = Material to be purchased
5,500 yards + 105,700 yards - 5,650 yards = 105,550 yards
Intended ending inventory plus the production-related materials minus the initial inventory equals the material to be bought.
Materials budget = Material to be purchased x Cost per yard
Materials budget = 105,550 yards x $5.80 per yard = $611,540
As a result, the annual materials budget is $611,540.
To know more about budget visit:-
https://brainly.com/question/27447669
#SPJ1
Which graph represents a linear function? !*100 Points*!

Answers
Answer:I only see one graph my guy but that is leaner
Step-by-step explanation:
what is the difference between ANOVA and Z-test Hypothesis
Answers
The difference between ANOVA and Z-test Hypothesis is the Z-test is employed to contrast the averages of single or dual populations, whereas ANOVA is utilized for assessing the means across three or more clusters.
How to determine the differenceThe Z-test becomes possible in the comparison of the mean of a sample to that of the population. It evaluates if there is statistical relevance in the difference between the mean of a sample and the mean of the whole population
In contrast, ANOVA is employed to contrast the averages of three or more separate groups. This assesses if there is a noteworthy distinction in the averages of said groups. The F-statistic in ANOVA is computed by assessing the disparity in variability between groups and the variability within groups.
In a nutshell, the Z-test is employed to contrast the averages of single or dual populations, whereas ANOVA is utilized for assessing the means across three or more clusters.
Learn more about ANOVA at: https://brainly.com/question/25800044
#SPJ1
HELP PLEASE NO LINKS OR FILES THEY WILL BE REPORTED

Answers
Answer:
One of the possible dimensions of the full trailer could be 5 by 12 by 3.
Step-by-step explanation:
Volume = weight times height times length = 12 times 5 times 3 = 180.
Ujalakhan01! Please help me! ASAP ONLY UJALAKHAN01. What's (x-1)(x-1)?
Answers
Answer:
\(x^2-2x+1\)
Step-by-step explanation:
=> (x-1)(x-1)
Using FOIL
=> \(x^2-x-x+1\)
=> \(x^2-2x+1\)
Answer:
Step-by-step explanation:
simply :
(x-1)(x-1)= (x-1)²= x²-2x=1
A new gaming chair costs $309.99. You have already saved $144.99 and earn $27.50 each week babysitting. Write and solve an equation to determine how many weeks, w, you must babysit to earn enough money to buy the new gaming chair.
27.5w − 144.99 = 309.99; w = 17
27.5 + 144.99w = 309.99; w = 6
27.5w − 309.99 = 144.99; w = 17
27.5w + 144.99 = 309.99; w = 6
Answers
The linear equation we need to solve is:
$27.50*w = $309.99 - $144.99
And the solution is w = 6.
How to write and solve the equation?
We know that the cost of the gaming chair is $309.99.
To buy this, you already have saved $144.99, and save another $27.50 per week, then the amount you have after w weeks is:
f(w) = $144.99 + $27.50*w
So the linear equation we need to solve is:
$144.99 + $27.50*w = $309.99
To solve this we need to isolate w.
$144.99 + $27.50*w = $309.99
$27.50*w = $309.99 - $144.99
w = ($309.99 - $144.99)/$27.50 = 6
So they can buy the chair after 6 weeks.
Learn more about linear equations at:
brainly.com/question/13763238
#SPJ1
Is n = -4.4 part of the solution set for n ÷ 2 < 4?

Answers
Answer:
Step-by-step explanation:

The point (2,0) lies on the graph of the function y = 2x^2 - 8x + 6.
A. True
B. False
Answers
y= 2(2)^2 -8(2)+6 = 2(4)-16+6 = 16 - 16 + 6 = 6
since y=6 and not 0, the answer is B (false)
What is the slope of this line?
a.−23
b.−13
c.13
d.23

Answers
Answer:
D
Step-by-step explanation:
I think you meant to put the answers as a fraction
Answer:
if there were slashes in between every answer, the answer would be
D. 2/3
Step-by-step explanation:
m = y2-y1 / x2-x1 (slope formula) ⋅the two points i used were: (0,-3) and (3,-1)
m = -1-(-3) / 3-0 (plug in the points)
m = -1+3 / 3-0
m = 2/3 (Simplify to get your answer)
Which statement defines an annuity?
Answers
Answer:
Annuity- A certain amount of money paid to somebody each year, usually for the rest of their life.
Step-by-step explanation:
Hope this helps.
Answer: A form of insurance or investments entitling the investor to a series of annual sums.
Step-by-step explanation:
Let A, B, C be three points with position vectors a, b, c respectively. You may assume that the three points A, B, C do not all lie on the same straight line. Let D, E, F be the midpoints of the line-segments BC, AC, AB respectively. What is the point with position vector 1/3 (a+b+c)?
Answers
The midpoint of three points with the position vector 1/3(a + b + c) is given by:
P = (b + c - B - C) / 2 + (1/3)(b + c)
The point with the position vector 1/3(a + b + c) is given by:
P = F - (2/3)D - (1/3)E + (1/3)(b + c)
To find the point with the position vector 1/3(a+b+c), we can use the fact that the position vector of a point that divides a line segment in a given ratio can be found by taking the weighted average of the position vectors of the endpoints.
Given that D, E, and F are the midpoints of line segments BC, AC, and AB, respectively, we know that:
D = (B + C) / 2
E = (A + C) / 2
F = (A + B) / 2
To find the point with the position vector 1/3(a+b+c), we can substitute a = 3F - 2D - E into the equation:
1/3(a + b + c) = 1/3((3F - 2D - E) + b + c)
Expanding the equation further:
1/3(a + b + c) = 1/3(3F - 2D - E + b + c)
= (F - (2/3)D - (1/3)E) + (1/3)(b + c)
Therefore, the point with the position vector 1/3(a + b + c) is given by:
P = F - (2/3)D - (1/3)E + (1/3)(b + c)
Substituting the midpoints:
P = (A + B) / 2 - (2/3)((B + C) / 2) - (1/3)((A + C) / 2) + (1/3)(b + c)
= (A + B - 2B - 2C - A - C + b + c) / 2 + (1/3)(b + c)
= (b + c - B - C) / 2 + (1/3)(b + c)
Therefore, the midpoint of three points with the position vector 1/3(a + b + c) is given by:
P = (b + c - B - C) / 2 + (1/3)(b + c)
The point with the position vector 1/3(a + b + c) is given by:
P = F - (2/3)D - (1/3)E + (1/3)(b + c)
For such more questions on midpoint of three points.
https://brainly.com/question/18226052
#SPJ11
Find the value of x in each case.

Answers
Student spend 5 minutes of every 60 minutes at school moving from class to class. Which fraction is equivalent to the number of minutes student spend moving from class to class?
Answers
Answer:
10/120
Step-by-step explanation:
Match the system of linear equations on the left with its solution type on the right
1. Y=2x-1
Y=2x+1
2. Y-4x=-2
Answers
Solution for the given System of linear equation is:
Infinite number of solution(2, -3)(-2, 4)Infinite number of solutionWhat are System of equation?Simultaneous equations, system of equations Two or more equations in algebra must be solved jointly (i.e., the solution must satisfy all the equations in the system). The number of equations must match the number of unknowns for a system to have a singular solution.
There are four methods to solving systems of equations: graphing, substitution, elimination and matrices.
Given, the system of linear equations on the left with its solution type on the right
For Y=2x-1 and Y=2x+1
Adding both equation, we will get y = 4x
Thus, these equations have infinite number of solution
For 2x - y = 7 and 3x + y = 3
Adding these equations
5x = 10
x= 2
Substitute the value in equation 1
y = -3
Thus, solution is (2, - 3)
therefore, the Solution for the given System of linear equation is:
Infinite number of solution(2, -3)(-2, 4)Infinite number of solutionLearn more about System of equation here:
https://brainly.com/question/12628931
#SPJ1
Complete question:

a line is perpendicular to y=-4x-2 and intersects the point (0,9). what is the equation for this perpendicular line?
Answers
Answer:
y=(1/4)x + 9 OR y=x/4 +9
Step-by-step explanation:
Perpendicular lines have a slope/gradient of -1/n
Because the slope of this line is -4, the slope of a line perpendicular to it would be 1/4.
y=(1/4)x+b
(0,9) is the y-intercept, so b = 9
y=(1/4)x + 9 OR y=x/4 +9
Part A
In the boxes provided, write three equations that can be solved to
find h, the number of hours it takes James to mow each of the
three lawns. Use h and = in each equation.
Equation for Mrs. Chavez's lawn:
Equation for Mr. Ortiz's lawn:
Equation for Mrs. White's lawn:
Answers
Answer:
Step-by-step explanation:
To find the number of hours for each, divide the amount of money he had received by the amount he would receive for 1 hour of work. (Answers are in the image below) I hope I wasn’t too late to help:)

Write an equation of a line that contains the following two points in slope intercept form
(-2,4) (3,-1)
Answers
Answer:
y = -x + 2
Step-by-step explanation:
The slope intercept form equation of this line can be written like this :
y = my + p ; where m is the slope and p is the y intercept.
\(m = \frac{-1-4}{3-(-2)} = \frac{-5}{5} =-1\)
then the equation becomes y = -x + p
(-2,4) is a point of the line means 4 = -(-2) + p
then p = 4 - 2 = 2
finally, y = -x + 2