Triangles ABC and DEF are similar. The lengths of the sides of ABC are 12, 15, and 20. The
length of the smallest side of DEF is 24. What is the length of the largest side of DEF?
Answers
Answer:
The length of the largest side of DEF is 40.
Step-by-step explanation:
Similar triangles' corresponding sides are proportional in length.
The smallest side of ABC is 12, and that is the corresponding side to the smallest side of DEF.
Calculate the proportional factor.
24 / 12 = 2.
Since similar triangles' sides are corresponding, the largest side of ABC will correspond with the largest side of DEF.
Calculate the largest side length.
20 * 2 = 40.
Related Questions
The vectors v and w lie in the coordinate plane such that their initial points are at the origin. Vector v has a magnitude of 2 and direction of 45° North of East. Vector w has a magnitude of 2 and a direction of 45° South of East. What is the magnitude of the vector v+w?
Answers
The vector v+w has a magnitude of 2√2 and its direction is along the positive x-axis.
What is meant by vector?
A vector is a quantity that has both magnitude and direction. It is represented as an arrow with its length representing the magnitude and its direction representing the direction of the quantity.
What is meant by the x-axis?
The x-axis is the horizontal line on a coordinate plane that is used as a reference for plotting and describing the positions of points in two-dimensional space. It is often referred to as the "horizontal axis" or the "abscissa".
According to the given information
Here the vector v has a magnitude of 2 and a direction of 45° so the components of vector v are:
v_x = 2 cos 45° = √2
v_y = 2 sin 45° = √2
Vector w has a magnitude of 2 and a direction of 45° South of East. This means that the angle between vector w and the positive x-axis is 45°, and the angle between vector w and the negative y-axis is 45°. Therefore, the components of vector w are:
w_x = 2 cos 45° = √2
w_y = -2 sin 45° = -√2
Now we can add the components of vectors v and w to find the components of the vector v+w:
(v+w)_x = v_x + w_x = √2 + √2 = 2√2
(v+w)_y = v_y + w_y = √2 - √2 = 0
To know more about x-axis visit
brainly.com/question/12032954
#SPJ1
To solve 1/3 divided by 9 James thinks of dividing a loaf of bread
Answers
Answer:
it would be 0.3 with bar notation
Step-by-step explanation:
Answer:
1/ 27
Step-by-step explanation:
Hope it helps

Write an equivalent expression by distributing the "−" sign outside the parentheses:
9.8w-(7x-1)
Answers
Answer:
9.8w-7x+1
Step-by-step explanation:
9.8w-(7x-1)
Distribute the minus sign to each term in the parenthesis
9.8w-7x - -1
A negative negative is a positive
9.8w-7x+1
Find the measure of angle AEB

Answers
Answer:
∠ AEB = 114°
Step-by-step explanation:
the chord- chord angle AEB is half the sum of the measures of the arcs intercepted by the angle and its vertical angle , that is
∠ AEB = \(\frac{1}{2}\) (AB + CD) = \(\frac{1}{2}\) (140 + 88)° = \(\frac{1}{2}\) × 228° = 114°
H Н
Which two statements are both true?
Di Ta and KFT
EH I TĞ and KT | TG
Di I K and Di 1 ET
ET I TĞ and KF | DI
Answers
A bag contains 3 blue marbles, 10 green marbles, 4 yellow marbles, and 8 red marbles. A marble is chosen at random, not replaced, then another marble is chosen. What is the probability that it is a red marble, then a blue marble? Write your answer as a fraction in simplest form.
Answers
Answer:
There are a total of 25 marbles in the bag.
The probability of choosing a red marble first is 8/25 since there are 8 red marbles out of 25 marbles in the bag.
Since a marble is not replaced after the first selection, there are now 24 marbles in the bag. There are still 3 blue marbles in the bag.
The probability of choosing a blue marble second, after a red marble has already been selected, is 3/24 or 1/8 since there are 3 blue marbles left out of 24 marbles in the bag.
To find the probability of both events occurring together, we multiply their individual probabilities:
8/25 x 1/8 = 1/25
Therefore, the probability that a red marble is chosen first, followed by a blue marble, is 1/25.
of 30 students, 1/3 play sports. of those who play sports,2/5 play soccer. How many students play soccer?
Answers
Answer: 4
Step-by-step explanation:
1 third of 30 is 10 and 2/5s of 10 is 4
When x=5, the value of the expression 20/-25+x-2(x-10)is
Answers
In the Gaussian integral, how does the left side of this equation equal the right side? An answer would be really appreciated, thank you.

Answers
the left side of this equation equal the right side through the process of completing the square that establishes the equality between the left side and the right side of the Gaussian integral equation.
How do we calculate?
using completing the square method:
Starting with the left side of the equation:
∫\(e^(^-^x^2)\) dx
\(e^(^-^x^2) = (e^(^-x^2/2))^2\)
∫\((e^(^-^x^2/2))^2 dx\)
let u = √(x²/2) = x = √(2u²).
dx = √2u du.
∫ \((e^(^x^2/2))^2 dx\)
= ∫ \((e^(^-2u^2)\)) (√2u du)
The integral of \(e^(-2u^2)\)= √(π/2).
∫ \((e^(-x^2/2))^2\) dx
= ∫ (√2u du) \((e^(-2u^2))\\\)
= √(π/2) ∫ (√2u du)
We substitute back u = √(x²/2), we obtain:
∫ \((e^(-x^2/2))^2\)dx
= √(π/2) (√(x²/2))²
= √(π/2) (x²/2)
= (√π/2) x²
A comparison with the right side of the equation shows that they are are equal.
Learn more about Gaussian integral equation at:
https://brainly.com/question/33550421
#SPJ1
What is the present value of R13 000 p.a. invested at the beginning of each year for 8years at 10%p.a. compound interest? (NB Use the compound interest tables provided or work to three decimal places only.)
Answers
Given statement solution is :- The present value of R13,000 per year invested for 8 years at 10% compound interest is approximately R69,776.60.
To calculate the present value of an investment with compound interest, we can use the formula for the present value of an annuity:
PV = A *\((1 - (1 + r)^(-n)) / r\)
Where:
PV = Present value
A = Annual payment or cash flow
r = Interest rate per period
n = Number of periods
In this case, the annual payment (A) is R13,000, the interest rate (r) is 10% per year, and the investment is made for 8 years (n).
Using the formula and substituting the given values, we can calculate the present value:
PV = \(13000 * (1 - (1 + 0.10)^(-8)) / 0.10\)
Calculating this expression:
PV = \(13000 * (1 - 1.10^(-8)) / 0.10\)
= 13000 * (1 - 0.46318) / 0.10
= 13000 * 0.53682 / 0.10
= 6977.66 / 0.10
= 69776.6
Therefore, the present value of R13,000 per year invested for 8 years at 10% compound interest is approximately R69,776.60.
For such more questions on present value
https://brainly.com/question/30390056
#SPJ8
Adams High School is going to select a committee. The committee will have a faculty member, a male student, a female student, a parent, and a school board member.
Here are the positions and the people interested in each.
Based on this list, how many ways are there to fill the five committee positions?
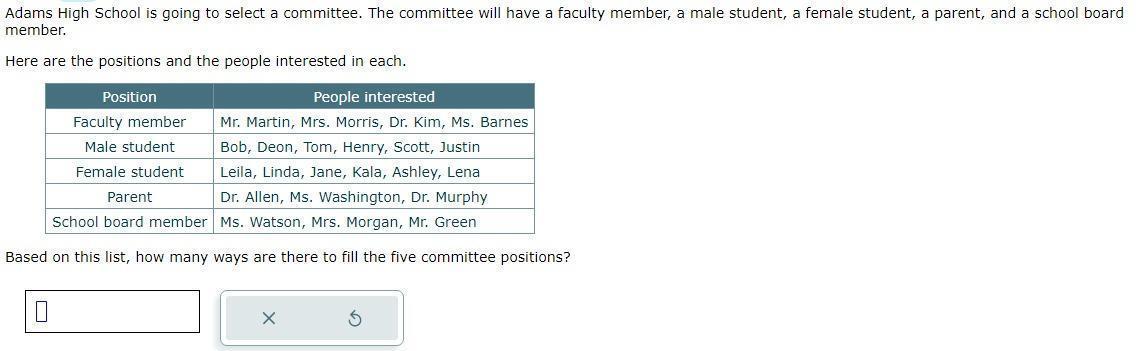
Answers
The number of ways to fill the five committee positions is 1296
How to determine the number of ways?from the question, we have the following parameters that can be used in our computation:
Faculty member = 4 members of staffMale students = 6Female students = 6Parent = 3School board member = 3The number of ways to fill the five committee positions is calculated as
Ways = Faculty member * Male students * Female students * Parent * School board member
So, we have
Ways = 4 * 6 * 6 * 3 * 3
Evaluate
Ways = 1296
Hence, there are 1296 ways
Read more about combination at
https://brainly.com/question/11732255
#SPJ1
Write an equivalent expression for 3x + 21
Answers
hope this helps
Find the measure of the indicated angle in each triangle.
A)37
B)63
C)80
D)180

Answers
m∠U = 80°
total interior angle in a triangle is 180°m∠U + 37° + 63° = 180°
m∠U = 180° - 63° - 37°
m∠U = 80°
m<U be x
Apply angle sum property
\(\\ \rm\rightarrowtail x+37+63=180\)
\(\\ \rm\rightarrowtail x+100=180\)
\(\\ \rm\rightarrowtail x=80\)
Please help me and answer that ??

Answers
Answer: A. 7/21 = 1/x
Step-by-step explanation: 7/21 = 1/3 so x would be 3.
Consider the curve given by the equation (2y+1)^3 − 24x = −3.
(a) Show that dy/dx = 4/(2y+1)^2.
(b) Write an equation for the line tangent to the curve at the point (−1,−2).
(c) Evaluate d2y/dx2 at the point (−1,−2).
(d) The point (16,0) is on the curve. Find the value of (y−1)′(0).
Answers
Answer:
(a) dy/dx = 4/(2y+1)^2.
(b) y = 4/9 x - 14/9
(c) d2y/dx2 = -64/243
Step-by-step explanation:
You have the following equation
\((2y+1)^3-24x=-3\) (1)
(a) You first derivative implicitly the equation (1) respect to x:
\(\frac{d}{dx}[(2y+1)^3-24x]=\frac{d}{dx}[-3]\\\\3(2y+1)^2(2\frac{dy}{dx})-24=0\)
next, you solve the last result for dy/dx:
\(6(2y+1)^2\frac{dy}{dx}=24\\\\\frac{dy}{dx}=\frac{4}{(2y+1)^2}\)(2)
(b) The equation for the tangent line is given by:
\(y-y_o=m(x-x_o)\) (3)
with yo = -2 and xo = -1
To find the slope m you use the result of the equation (2), because dy/dx evaluated in (-1,-2) is the slope at such point:
m = \(\frac{dy}{dx}=\frac{4}{(2(-2)+1)^2}=\frac{4}{9}\)
Hence, by replacing in the equation (3) you obtain:
\(y-(-2)=\frac{4}{9}(x-(-1))\\\\y+2=\frac{4}{9}x+\frac{4}{9}\\\\y=\frac{4}{9}x-\frac{14}{9}\)
hence, the equation for the tangent line is y = 4/9 x - 14/9
(c) To find d2y/dx2 you derivative the result obtain in the equation (2):
\(\frac{d^2y}{dx^2}=\frac{d}{dx}[4(2y+1)^{-2}]\\\\\frac{d^2y}{dx^2}=-8(2y+1)^{-3}(2\frac{dy}{dx})\\\\\frac{d^2y}{dx^2}=-16(2y+1)^{-3}\frac{dy}{dx}\) (4)
the second derivative for the point (-1,-2) is obtained by replacing y=-2 and dy/dx=m=4/9 in the equation (4):
\(\frac{d^2y}{dx^2}=-16(2(-2)+1)^{-3}(\frac{4}{9})=-\frac{64}{243}\)
hence, d2y/dx2 evaluated in (-1,-2) is -64/243
Answer:
(A) The value of \(dy/dx=\frac{4}{(2y+1)^2}\).
(B) The equation of the tangent is : \(y=(4/9)x-(14/9)\)
(C) The value of \(\frac{d^2y}{dx^2}=-64/243\)
(D) The point (16,0) is not on curve so it can not be determined by the given equation.
Step-by-step explanation:
Given information:
The equation \((2y+1)^3-24x=-3\)
(A) For the first derivative of the given equation:
\(\frac{d}{dx}[(2y+1)^3-24x ]= \frac{d}{dx}(-3)\)
\(3(2y+1)^2(dy/dx)-24=0\)
\((dy/dx)=\frac{4}{(2y+1)^2}\)
Hence , from the above equation it is shown that the value of
\(dy/dx=\frac{4}{(2y+1)^2}\)
(B) The equation of the tangent to the curve is given by:
\(y-y_o=m(x-x_0)\\\)
On putting the given values in the above equation
We get:
\(m=\frac{4}{(2(-2))+1)^2}\)
\(m=4/9\)
Hence, the equation of the tangent can be written as :
\(y-(-2)=(4/9)(x-(-1))\\y+2=\frac{4}{9}x+\frac{4}{9}\)
So, the equation of the tangent is :
\(y=(4/9)x-(14/9)\)
(C) Now ,
To find \(d^2y/dx^2\) for the equation
We have to find double derivative of the equation;
\(\frac{d^2y}{dx^2} =\frac{d}{dx}[4(2y+1)^{-2}]\\\frac{d^2y}{dx^2} = -16(2y+1)^{-3}\frac{dy}{dx}\)
On putting the values from the given information in the above equation;
\(\frac{d^2y}{dx^2} =-16(2(-2)+1)^{-3}(4/9)\)
\(\frac{d^2y}{dx^2}=-64/243\)
(D) For the equation \((2y+1)^3-24x=-3\)
First check for the given points (16,0) if it satisfies the given equation or not.
Now on checking for the same the point is not satisfying the given equation hence, we can not find the value of \((y-1)'(0)\).
For more information visit:
https://brainly.com/question/5797309?referrer=searchResults
What is the domain of the function graphed below

Answers
Answer: Option 1
Step-by-step explanation:
The domain is the set of all x values.
Battery life for a hand-held computer is normally distrituted and has a population standard deviation of 7 hours. Suppose you need to estimate a confidence interval estimate at the 95% level of confidence for the mean life of these batteries. Determine the sample size required to have a margin of error of 0.585 hours. Round up to the nearest whole number.
Answers
Answer:
A sample size of 551 is required.
Step-by-step explanation:
We have that to find our \(\alpha\) level, that is the subtraction of 1 by the confidence interval divided by 2. So:
\(\alpha = \frac{1 - 0.95}{2} = 0.025\)
Now, we have to find z in the Ztable as such z has a pvalue of \(1 - \alpha\).
That is z with a pvalue of \(1 - 0.025 = 0.975\), so Z = 1.96.
Now, find the margin of error M as such
\(M = z\frac{\sigma}{\sqrt{n}}\)
In which \(\sigma\) is the standard deviation of the population and n is the size of the sample.
Population standard deviation of 7 hours.
This means that \(\sigma = 7\)
Determine the sample size required to have a margin of error of 0.585 hours.
This is n for which M = 0.585. So
\(M = z\frac{\sigma}{\sqrt{n}}\)
\(0.585 = 1.96\frac{7}{\sqrt{n}}\)
\(0.585\sqrt{n} = 1.96*7\)
\(\sqrt{n} = \frac{1.96*7}{0.585}\)
\((\sqrt{n})^2 = (\frac{1.96*7}{0.585})^2\)
\(n = 550.04\)
Rounding up(as for a sample of 550 the margir of error will be a bit above the desired target):
A sample size of 551 is required.
What is the slop of the line that contains the points (0,1)and(-2,-9).write your answer as a friction in simplest from (hint:2/1 should be simplified to 2
Answers
Answer:
5
Step-by-step explanation:
To find the slope we will use the slope formula:
\(slope = \frac{y2 - y1}{x2 - x1}\)
They give us the points of (0,1) and (-2,-9) in the equation. Let's label each thing to fit the equation:
y2 = -9
y1 = 1
x2 = -2
x1 = 0
Now, plug it all in to the equation:
\(\frac{-9-1}{-2-0} = \frac{-10}{-2} = 5\)
Therefore, the slope is 5.
I hope this helps!!
- Kay :)
Let Y1 and Y2 denote the proportion of time during which employees I and II actually performed their assigned tasks during a workday, The joint density of Y1 and Y2 is given by
f(y1,y2) = { y1+y2, 0<=y1<=1, 0<=y2<=1, 0, elsewhere
Required:
a. Find the marginal density function of Y1 and Y2
b. Find P(Y1 >= 1/2 | Y2 >= 1/2).
c. If employee II spends exactly 50% of the dayworking on assigned duties, find the probability that employee I spends more than 75% of the day working on similarduties.
Answers
Answer:
Step-by-step explanation:
From the information given:
The joint density of \(y_1\) and \(y_2\) is given by:
\(f_{(y_1,y_2)} \left \{ {{y_1+y_2, \ \ 0\ \le \ y_1 \ \le 1 , \ \ 0 \ \ \le y_2 \ \ \le 1} \atop {0, \ \ \ elsewhere \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \right.\)
a)To find the marginal density of \(y_1\).
\(f_{y_1} (y_1) = \int \limits ^{\infty}_{-\infty} f_{y_1,y_2} (y_1 >y_2) \ dy_2\)
\(=\int \limits ^{1}_{0}(y_1+y_2)\ dy_2\)
\(=\int \limits ^{1}_{0} \ \ y_1dy_2+ \int \limits ^{1}_{0} \ y_2 dy_2\)
\(= y_1 \ \int \limits ^{1}_{0} dy_2+ \int \limits ^{1}_{0} \ y_2 dy_2\)
\(= y_1[y_2]^1_0 + \bigg [ \dfrac{y_2^2}{2}\bigg]^1_0\)
\(= y_1 [1] + [\dfrac{1}{2}]\)
\(= y_1 + \dfrac{1}{2}\)
i.e.
\(f_{(y_1}(y_1)}= \left \{ {{y_1+\dfrac{1}{2}, \ \ 0\ \ \le \ y_1 \ \le , \ 1} \atop {0, \ \ \ elsewhere \ \\ \ \ \ \ \ \ \ \ } \right.\)
The marginal density of \(y_2\) is:
\(f_{y_1} (y_2) = \int \limits ^{\infty}_{-\infty} fy_1y_1(y_1-y_2) dy_1\)
\(= \int \limits ^1_0 \ y_1 dy_1 + y_2 \int \limits ^1_0 dy_1\)
\(=\bigg[ \dfrac{y_1^2}{2} \bigg]^1_0 + y_2 [y_1]^1_0\)
\(= [ \dfrac{1}{2}] + y_2 [1]\)
\(= y_2 + \dfrac{1}{2}\)
i.e.
\(f_{(y_1}(y_2)}= \left \{ {{y_2+\dfrac{1}{2}, \ \ 0\ \ \le \ y_1 \ \le , \ 1} \atop {0, \ \ \ elsewhere \ \\ \ \ \ \ \ \ \ \ } \right.\)
b)
\(P\bigg[y_1 \ge \dfrac{1}{2}\bigg |y_2 \ge \dfrac{1}{2} \bigg] = \dfrac{P\bigg [y_1 \ge \dfrac{1}{2} . y_2 \ge\dfrac{1}{2} \bigg]}{P\bigg[ y_2 \ge \dfrac{1}{2}\bigg]}\)
\(= \dfrac{\int \limits ^1_{\frac{1}{2}} \int \limits ^1_{\frac{1}{2}} f_{y_1,y_1(y_1-y_2) dy_1dy_2}}{\int \limits ^1_{\frac{1}{2}} fy_1 (y_2) \ dy_2}\)
\(= \dfrac{\int \limits ^1_{\frac{1}{2}} \int \limits ^1_{\frac{1}{2}} (y_1+y_2) \ dy_1 dy_2}{\int \limits ^1_{\frac{1}{2}} (y_2 + \dfrac{1}{2}) \ dy_2}\)
\(= \dfrac{\dfrac{3}{8}}{\dfrac{5}{8}}\)
\(= \dfrac{3}{8}}\times {\dfrac{8}{5}}\)
\(= \dfrac{3}{5}}\)
= 0.6
(c) The required probability is:
\(P(y_2 \ge 0.75 \ y_1 = 0.50) = \dfrac{P(y_2 \ge 0.75 . y_1 =0.50)}{P(y_1 = 0.50)}\)
\(= \dfrac{\int \limits ^1_{0.75} (y_2 +0.50) \ dy_2}{(0.50 + \dfrac{1}{2})}\)
\(= \dfrac{0.34375}{1}\)
= 0.34375
Which statement describes the relationship between x
and y?
As x increases, y decreases.
QAs x increases, y increases.
O As x increases, y increases and then decreases.
As x increases, y decreases and then increases.

Answers
Answer:
1.) inverse proportion : 1kx = y
2) direct proportion. y = kx
find 7x +y when x=7 and y=1
Answers
Answer:
7x+y
7(7)+1
49+1
50
Step-by-step explanation:
please mark me as brainlest
Answer:
7x + y
x=7 y=1
7(7) + 1
49 + 1
= 50
Solve for x by writing the equation in exponential form.
log₁₆ x=-1/2
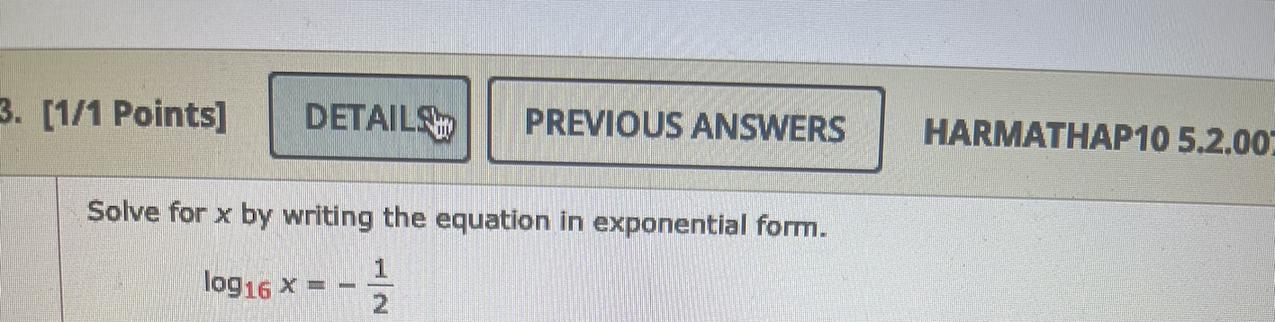
Answers
The solution for x in the given logarithmic equation, log₁₆x = -1/2, is x = 1/4
Solving logarithmic equationsFrom the question, we are to solve the given equation for x.
The given equation is
log₁₆x = -1/2
To solve the equation, we will determine the value of x.
Solving the equation
log₁₆x = -1/2
From one of the laws of logarithm,
logₐy = n ⇒ y = aⁿ
Thus,
The equation becomes
x = 16^(-1/2)
By applying one of the laws of indices, we get
x = (√16)⁻¹
x = 4⁻¹
x = 1/4
Hence, the value of x is x =1/4
Learn more on Solving equations here: https://brainly.com/question/28041634
#SPJ1
Write the solution of one-half of two-thirds of three out of four-fifths of 200
Answers
Answer:
53 1/3
Step-by-step explanation:
200×4/5=160
160×2/3=106 2/3
106 2/3×1/2=53 1/3
Step-by-step explanation:
200×1/2=100
100×2/3=66.6666666667
so, the question is wrong
Help pls pls pls pls

Answers
Answer:
angle 5 and angle 2
angle 1 and angle 4 + 3
(a) Un ángulo mide 47°. ¿Cuál es la medida de su complemento?
(b) Un ángulo mide 149°. ¿Cuál es la medida de su suplemento?
Answers
El supplemento y el complemento de cada ángulo son, respectivamente:
Caso A: m ∠ A' = 43°
Caso B: m ∠ A' = 31°
¿Cómo determinar el complemento y el suplemento de un ángulo?De acuerdo con la geometría, la suma de un ángulo y su complemento es igual a 90° and la suma de un ángulo y su suplemento es igual a 180°. Matemáticamente hablando, cada situación es descrita por las siguientes formulas:
Ángulo y su complemento
m ∠ A + m ∠ A' = 90°
Ángulo y su suplemento
m ∠ A + m ∠ A' = 90°
Donde:
m ∠ A - Ángulom ∠ A' - Complemento / Suplemento.Ahora procedemos a determinar cada ángulo faltante:
Caso A: Complemento
47° + m ∠ A' = 90°
m ∠ A' = 43°
Caso B: Suplemento
149° + m ∠ A' = 180°
m ∠ A' = 31°
ObservaciónEl enunciado se encuentra escrito en español y la respuesta está escrita en el mismo idioma.
The statement is written in Spanish and its answer is written in the same language.
Para aprender más sobre ángulos complementarios y suplementarios: https://brainly.com/question/4410854
#SPJ1
The fraction of PKR 1 is 50 paisas
Answers
The fraction that represents the rate between PKR and Paisas is given as follows:
1/50.
What is a fraction?A fraction is a numerical representation of the division of the two terms x and y, as follows:
Fraction = x/y.
As the rate is PKR 1 = 50 paisas, we have that the fraction that represents the rate between PKR and Paisas is given as follows:
1/50.
More can be learned about fractions at brainly.com/question/1622425
#SPJ1
Answer this question please

Answers
Answer:
Step-by-step explanation:
we know this is a 2 dimensional shape so m*3 out, its m not ft so only answer is
24 m*2
Find the indicated measure.
Radius of a circle with an area of 380 square inches
Answers
The radius of the circle that has an area of 380 square inches is calculated as: 11 inches.
What is the Radius of a Circle?The radius of a circle is half of the diameter. It connects from the center of the circle to any point on the circumference on the circle.
We are given the following information about a circle:
Area of the circle = 380 square inches
To find the radius of the circle, recall the formula of the area of a circle which is:
area = πr², where r is the radius, π = 3.14
Therefore:
380 = πr²
380 = 3.14 * r²
380/3.14 = r²
r² = 121.01
r = √121.01
r = 11 inches.
Learn more about the radius of a circle on:
https://brainly.com/question/28162977
#SPJ1
Evaluate -7 1/3 - (-2/5)=
Answers
Answer:
-7 1/3 - (-2/5)
Step-by-step explanation:
-22/3 + 2/5
(-110+6)/15
-104/15
-6. 933
ans is -6. 933
Answer: -104/5
Step-by-step explanation:
-22/3 + 2/5 = -104/15
Evaluate the expression if a = 3, b = 5, and c = 6.
c^2 + 3a × b

Answers
Answer:
81 is your answer.☺Step-by-step explanation:
a = 3, b = 5, and c = 6
c^2 + 3a × b
6^2 + 3(3) × 5
36+9×5
36+45
81 => Ans
Hope this helps
Keep Smiling :)