Trey is selling raffle tickets. For every 4 tickets, he charges $24 . Complete the table below showing the number of tickets and the amount Trey charges.

Answers
$24 / 4 tickets = $6 per 1 ticket
With that information, we can calculate the rest through simple evaluation. That would look like so:
7 tickets • $6 per ticket = $42 for 7 tickets
$54 / $6 per ticket = 9 tickets for $54
10 tickets • $6 per ticket = $60 for every 10 tickets
Answer Recap: The answers, from left to right, would be 1, 42, 9, and 60.
Related Questions
Evaluate the function f(x) = 4x-6 at the given values of the independent variable and simplify

Answers
In general, to evaluate the function f(x) at a specific value of x, we substitute that value into the expression for f(x) and simplify.
What is function?In mathematics, a function is a relation between two sets, where for every element in the first set (called the domain), there is exactly one element in the second set (called the range) that the function maps to. In simpler terms, a function is a rule that assigns each input value from the domain to exactly one output value in the range. Functions are usually represented by a formula or equation that describes the relationship between the input and output values. For example, the function f(x) = 2x + 1 maps every input value of x to an output value that is twice the input value plus 1.
Here,
To evaluate the function f(x) = 4x - 6, we substitute the given values of the independent variable into the expression for f(x) and simplify.
For example:
f(0) = 4(0) - 6 = -6
f(1) = 4(1) - 6 = -2
f(2) = 4(2) - 6 = 2
f(-1) = 4(-1) - 6 = -10
f(3a) = 4(3a) - 6 = 12a - 6
To know more about function,
https://brainly.com/question/28278690
#SPJ1
Find the missing number to complete the linear equation that gives the rule for this table
This is 7th grade accelerated math
Pls help ASAP this is due soon

Answers
Answer:
Y=25x
Step-by-step explanation:
Cross multiply
75/3=25
50/2=25
25/1=25
Ans: 25
Answer:
y= 25x.
Step-by-step explanation:
This is direct variation because y/x = 25/1 = 50/2 = 75/3 = 25 , and when x = 0 y = 0.
So the equation is y = 25x.
a raised rectangular garden is two feet more than three times as long as it is wide. the depth of the pool is half the width. if the length is 11 feet, what is the volume?
Answers
Answer:
49.5ft³
Step-by-step explanation:
If it is 2 ft more than 3 times as long as it is wide then:
l = 3w + 2
which means:
w = (l-2)/3
and:
d = 1/2((l-2)/3)
Now just substitute in 11 for l
w = (11 - 2)/3
w = 9/3
w = 3
d = 1/2((11-2)/3)
d = 1/2(9/3)
d = 1/2(3)
d = 1.5
So the total volume is:
11 * 3 * 1.5
49.5
What is the value of the
expression shown?
28 - 62
Answers
Answer:
-34........................

The graph compares the scores earned by 100 students on a pre-test and a post-test.
Two box and whisker plots showing Pre-Test and Post-Test scores on a number line from 0 to 100. The upper plot represents the pre-test scores. For this upper plot, the minimum number is 0, the maximum number is 78, the right side of the box is 60, the left side of the box is 16, and the bar in the box is at 30. The lower plot represents the post-test scores. For this lower plot, the minimum number is 4, the maximum number is 100, the right side of the box is 83, the left side of the box is 30, and the bar in the box is at 45.
About how many more students scored greater than 30% on the post-test than on the pre-test?
15

Answers
Answer:
25 more studentsStep-by-step explanation:
30% mark represents:
50% on pre-test and 25% on post test.So
50% of 100 = 50 students scored greater than 30%75% of 100 = 75 students scored greater than 30%.The difference is:
75 - 50 = 25 studentsAnswer:
25 students
Step-by-step explanation:
1. Given the scalar field, (x, y, z)=x²y + 2yz². Find the directional derivativative of (x, y, z) at the point Q(1,-1,1) in Q(1,-1,1) in the direction of a = -2i-j+2k. Hence, obtain the direction and the maximum change of p(x, y, z) at the point Q. Ans: Do== √29, Vo=(-2,3,-4)
Answers
The directional derivative of the scalar field p(x, y, z) = x²y + 2yz² at the point Q(1, -1, 1) in the direction of a = -2i - j + 2k is √29. The direction of maximum change of p(x, y, z) at the point Q is Vo = (-2, 3, -4).
The directional derivative of a scalar field in the direction of a unit vector u is given by
```
Dp(u) = ∇p(x, y, z) ⋅ u
```
where ∇p is the gradient of p. The gradient of p is a vector that points in the direction of the steepest ascent of p, and its magnitude is the rate of change of p in that direction.
In this case, the gradient of p is
```
∇p = (2xy + 2yz, x² - 2z², 2x²y)
```
The unit vector in the direction of a is
```
u = 1/√29 (-2, -1, 2)
```
Therefore, the directional derivative of p in the direction of a is
```
Dp(u) = ∇p ⋅ u = √29
```
This means that the rate of change of p in the direction of a is √29. The direction of maximum change of p at the point Q is the same as the direction of a, which is (-2, -1, 2).
Learn more about directional derivative here:
brainly.com/question/29451547
#SPJ11
Suppose we have 4 email messages. We have also classified 3 messages as normal and 1 as spam. Use Naïve Bayes multinomial to answer the question that follows. Use alpha=1 to avoid zero probabilities.
Message Content Classification
1 Chinese Beijing Chinese Normal
2 Chinese Chinese Shanghai Normal
3 Chinese Macao Normal
4 Tokyo Japan Chinese Spam
Round your answer to the nearest ten thousand
P(Tokyo | Spam)
Answers
Using Naïve Bayes multinomial with alpha=1, we classify the given messages based on their content. Message 4, "Tokyo Japan Chinese," is classified as spam.
To classify the messages using Naïve Bayes multinomial, we consider the content of the messages and their corresponding classifications. We calculate the probabilities of each message belonging to the "Normal" or "Spam" classes.
3 messages are classified as "Normal."
1 message is classified as "Spam."
We calculate the probabilities as follows:
P(Class = Normal) = 3/4 = 0.75
P(Class = Spam) = 1/4 = 0.25
Next, we analyze the occurrence of words in each class:
For the "Normal" class:
The word "Chinese" appears 5 times.
The word "Beijing" appears 1 time.
The word "Shanghai" appears 1 time.
The word "Macao" appears 1 time.
For the "Spam" class:
The word "Tokyo" appears 1 time.
The word "Japan" appears 1 time.
The word "Chinese" appears 1 time.
Now, we calculate the probabilities of each word given the class using Laplace smoothing (alpha=1):
P(Chinese|Normal) = (5 + 1)/(5 + 4) = 6/9
P(Beijing|Normal) = (1 + 1)/(5 + 4) = 2/9
P(Shanghai|Normal) = (1 + 1)/(5 + 4) = 2/9
P(Macao|Normal) = (1 + 1)/(5 + 4) = 2/9
P(Tokyo|Spam) = (1 + 1)/(3 + 4) = 2/7
P(Japan|Spam) = (1 + 1)/(3 + 4) = 2/7
P(Chinese|Spam) = (1 + 1)/(3 + 4) = 2/7
To classify Message 4, "Tokyo Japan Chinese," we compute the probabilities for each class:
P(Normal|Message 4) = P(Chinese|Normal) * P(Tokyo|Normal) * P(Japan|Normal) * P(Class = Normal)
≈ (6/9) * (0/9) * (0/9) * 0.75
= 0
P(Spam|Message 4) = P(Chinese|Spam) * P(Tokyo|Spam) * P(Japan|Spam) * P(Class = Spam)
≈ (2/7) * (2/7) * (2/7) * 0.25
≈ 0.017
Since P(Spam|Message 4) > P(Normal|Message 4), we classify Message 4 as spam.
In summary, using Naïve Bayes multinomial with alpha=1, we classify Message 4, "Tokyo Japan Chinese," as spam based on its content.
Learn more about probabilities: brainly.com/question/13604758
#SPJ11
Using Naïve Bayes multinomial with alpha=1, we classify the given messages based on their content. Message 4, "Tokyo Japan Chinese," is classified as spam.
To classify the messages using Naïve Bayes multinomial, we consider the content of the messages and their corresponding classifications. We calculate the probabilities of each message belonging to the "Normal" or "Spam" classes.
3 messages are classified as "Normal."
1 message is classified as "Spam."
We calculate the probabilities as follows:
P(Class = Normal) = 3/4 = 0.75
P(Class = Spam) = 1/4 = 0.25
Next, we analyze the occurrence of words in each class:
For the "Normal" class:
The word "Chinese" appears 5 times.
The word "Beijing" appears 1 time.
The word "Shanghai" appears 1 time.
The word "Macao" appears 1 time.
For the "Spam" class:
The word "Tokyo" appears 1 time.
The word "Japan" appears 1 time.
The word "Chinese" appears 1 time.
Now, we calculate the probabilities of each word given the class using Laplace smoothing (alpha=1):
P(Chinese|Normal) = (5 + 1)/(5 + 4) = 6/9
P(Beijing|Normal) = (1 + 1)/(5 + 4) = 2/9
P(Shanghai|Normal) = (1 + 1)/(5 + 4) = 2/9
P(Macao|Normal) = (1 + 1)/(5 + 4) = 2/9
P(Tokyo|Spam) = (1 + 1)/(3 + 4) = 2/7
P(Japan|Spam) = (1 + 1)/(3 + 4) = 2/7
P(Chinese|Spam) = (1 + 1)/(3 + 4) = 2/7
To classify Message 4, "Tokyo Japan Chinese," we compute the probabilities for each class:
P(Normal|Message 4) = P(Chinese|Normal) * P(Tokyo|Normal) * P(Japan|Normal) * P(Class = Normal)
≈ (6/9) * (0/9) * (0/9) * 0.75
= 0
P(Spam|Message 4) = P(Chinese|Spam) * P(Tokyo|Spam) * P(Japan|Spam) * P(Class = Spam)
≈ (2/7) * (2/7) * (2/7) * 0.25
≈ 0.017
Since P(Spam|Message 4) > P(Normal|Message 4), we classify Message 4 as spam.
In summary, using Naïve Bayes multinomial with alpha=1, we classify Message 4, "Tokyo Japan Chinese," as spam based on its content.
Learn more about probabilities: brainly.com/question/13604758
#SPJ11
A rose garden in the city park is rectangular and is 9 m wide. If the area of the rectangle is 144 m², what is the length of the garden?
Answers
Answer:
Length = 16m
Step-by-step explanation:
Area of a rectangle = Length * Width
144m^2 = Length * 9m
Divide both sides by 9m
Length = 16m
Comparing Ratios from Tables
Squares
5
10
Squares
10
20
Table A
Table B
Circles
3
6
Circles
3
9
Which statement is true about the ratios of squares to
circles in the tables?
The ratios in Table A are greater than the ratios in
Table B.
The ratios in Table B are greater than the ratios in
Table A.
Only some of the ratios in Table A are greater than
the ratios in Table B.
The ratios in Table A are equal to the ratios in Table
B.
Answers
We can conclude that only some of the ratios in Table A are greater than the ratios in Table B. (option-c)
To compare the ratios of squares to circles in the tables, we must divide the value in the Squares column by the value in the Circles column for each row in the table.
For Table A, the ratios of squares to circles are:
5/3 = 1.67
10/6 = 1.67
For Table B, the ratios of squares to circles are:
10/3 = 3.33
20/9 = 2.22
Comparing the ratios in Table A to the ratios in Table B, we see that the first two ratios are equal (1.67) and the last two ratios are different (3.33 in Table B is greater than 1.67 in Table A, and 2.22 in Table B is less than 1.67 in Table A).
Specifically, the ratio in the second row of Table B is greater than both ratios in Table A, but the ratios in the first row of each table are equal.(option-c)
For such more questions on ratio
https://brainly.com/question/12024093
#SPJ8
Find the missing angle.
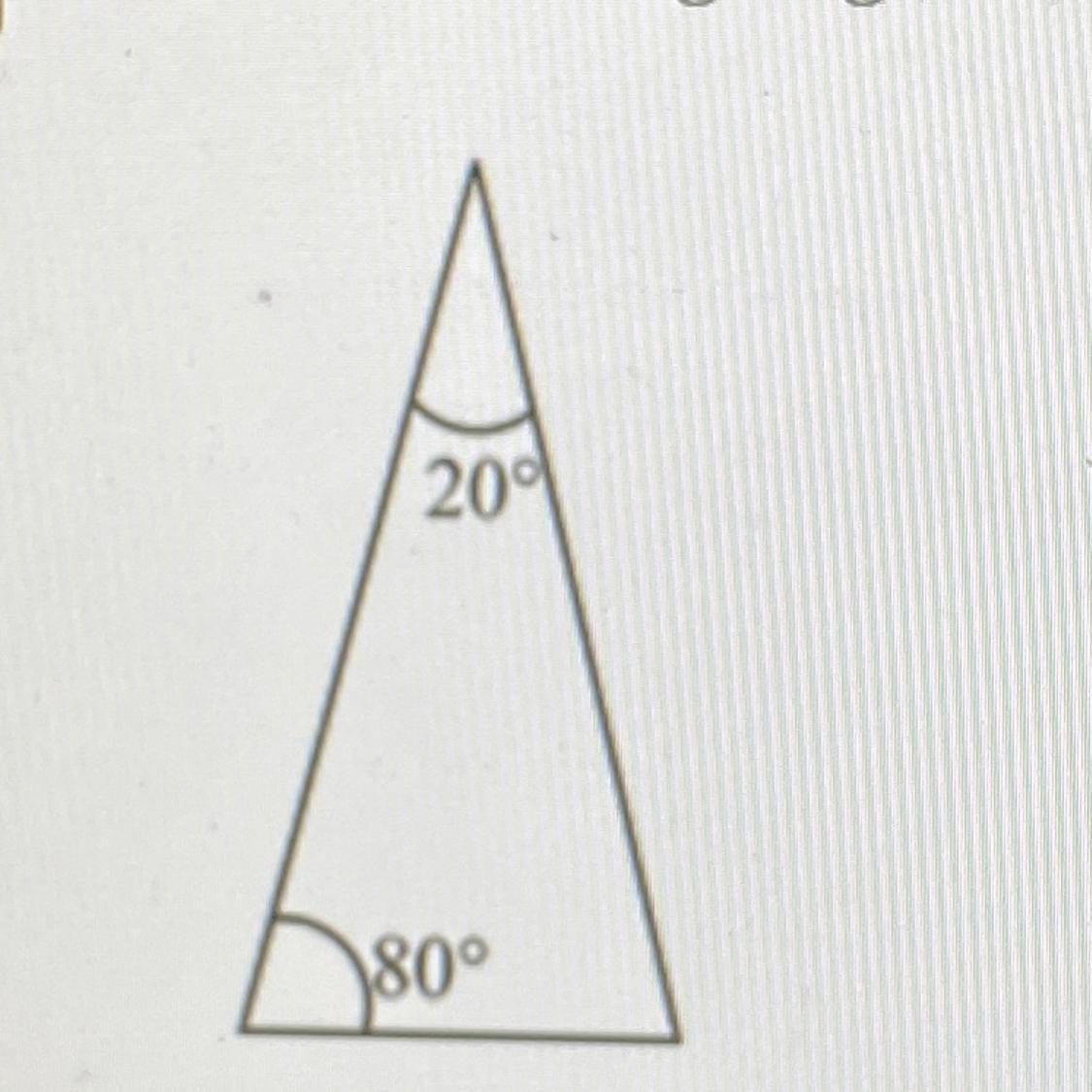
Answers
Answer:
\(x=80\)°
Step-by-step explanation:
\(sum ~of ~3~angles ~of ~a~ triangle ~is ~180\)
\(80+20+x=180\)
\(x=missing ~angle\)
\(100+x=180\)
\(x=180-100=80\)
\(So, x=80\)
-------------------------
hope it helps...
have a great day!!
Multiple
(3x – 4)(2x²–5x+1)
Answers
The Answer is
6x^3 - 23x^2 + 23x - 4
Which inequality is true?
O A. |-15| > |-19
OB. |-161 < 1131
OC. |-15] > [12
OD. 12< |-81
O E. |-19| > |-201
Answers
Answer:
Taking the absolute value results in a positive value A would be trueMe miles burrow lies 5 meters below ground. He started digging his way deeper into the ground. Descending 3 meters each minute. Graph the relationship between Mr. Moles elevation relative to the ground (in meters) and in time (in minutes)
Answers
Answer:
y= -3x-5
Step-by-step explanation:
Since your 5 m below, it is -5
The rate of change is 3 but since your going down, it is -3.
Hope this helps and sorry I can't graph this but you can use the equation to help
what is the arclength of \(r(x)=(6x^2, 2\sqrt{6} x , lnx) for 1\leq x\leq 6\)
Answers
Differentiate r(x) :
\(r'(x) = \left(12x,2\sqrt 6,\dfrac1x\right)\)
Then the arc length of r(x) over 1 ≤ x ≤ 6 is given by the integral,
\(\displaystyle \int_1^6 \|r'(x)\|\,\mathrm dx = \int_1^6 \sqrt{(12x)^2 + (2\sqrt6)^2 + \left(\frac1x\right)^2} \,\mathrm dx = \int_1^6 \sqrt{144x^2 + 24 + \frac1{x^2}}\,\mathrm dx\)
Notice that the expression in the square root is a perfect square:
\(144x^2 + 24 + \dfrac1{x^2} = (12x)^2 + 2\cdot12x\cdot\dfrac1x + \left(\dfrac1x\right)^2 = \left(12x+\dfrac1x\right)^2\)
Then in the integral, we have
\(\displaystyle \int_1^6 \sqrt{\left(12x+\frac1x\right)^2}\,\mathrm dx = \int_1^6 \left|12x + \frac1x\right|\,\mathrm dx\)
but the integrand is positive over its entire domain, so we can drop the absolute value.
The arc length is then
\(\displaystyle \int_1^6 \left(12x+\frac1x\right)\,\mathrm dx = (6x^2 + \ln|x|)\bigg|_1^6 = (6^3+\ln(6)) - (6+\ln(1)) = \boxed{210+\ln(6)}\)
Javier drinks 8 cups of water in one day.What is the unit rate of cups of water to days?
Answers
The unit rate here is also 8 cups of water per day.
We need to remember that in the unit rate we have as the denominator one unit of any quantity.
In this case, we have a day as the denominator one day, since:
\(\frac{8cupofwater}{1\text{day}}\)In summary, therefore, the unit rate, in this case, is 8 cups of water per day:

A transit system contains the blue line. The blue line has 7 cars and averages 450 passengers per run. Calculate the huntington-hill number for the blue line.
Answers
The total number of passengers (3150) by the geometric mean (5.71), resulting in approximately 550.81. The nth root of the product of the number of passengers in each car, where n is the number of cars.
To calculate the Huntington-Hill number for the blue line of the transit system, we need to divide the total number of passengers by the geometric mean of the population of each car. In this case, the blue line has 7 cars and averages 450 passengers per run.
So, the total number of passengers for the blue line would be 7 cars multiplied by 450 passengers per run, which equals 3150 passengers.
To find the geometric mean of the population of each car, we take the nth root of the product of the number of passengers in each car, where n is the number of cars.
So, the geometric mean for the blue line would be the seventh root of 450 passengers per run, which is approximately 5.71 passengers.
Finally, to calculate the Huntington-Hill number, we divide the total number of passengers (3150) by the geometric mean (5.71), resulting in approximately 550.81.
To know more about geometric mean visit:-
https://brainly.com/question/29199001
#SPJ11
8. Maximize p=x+2y subject to 30x+20y
0.1x+0.4y
0.2x+0.3y
x≥0,y≥0
Answers
Answer:5.97
Step-by-step explanation.
you have to look at the question.
you have to look around the question
The very last step is you have to answer it
The map scale is 1 cm = 3 miles. If the distance between my house and school is 4.5 cm on the map, how far is the actual distance?
Answers
the answer is 13.5 miles

Which choice is equivalent to the quotient shown here for acceptable
values of x?
√12(x-1)+√√2(x-1)²

Answers
For acceptable x values of √12(x-1)+√√2(x-1)², the option is equivalent to the quotient given here (x-1) ² is \($2 \sqrt{3} \sqrt{x-1}-\sqrt{2}(x-1)$\\\) .
How do you find the quotient of a set?The equivalent of the quotient displayed above for allowable x values is
\($\sqrt{1} \cdot 2(x-1)+\sqrt{\sqrt{2}}(x-1)^2$\)
\($2(x-1)+\sqrt[2 \cdot 2]{2}(x-1)^2$\\\)
\(\$2(x-1)+\sqrt[4]{2}(x-1)^2$\\$(2 x-2)+\sqrt[4]{2}\left(x^2+2 x(-1)+(-1)^2\right)$\\$(2 x-2)+\sqrt[4]{2}\left(x^2-2 x+1\right)$\\$2 x-2+\sqrt[4]{2}\left(x^2-2 x+1\right)$\\$2 x+\sqrt[4]{2}\left(x^2-2 x+1\right)-2$\\$2 x+\left(\sqrt[4]{2} \cdot x^2-\sqrt[4]{2} \cdot 2 x+\sqrt[4]{2}\right)-2$\\$2 x+\left(\sqrt[4]{2} \cdot x^2-2 \cdot \sqrt[4]{2} \cdot x+\sqrt[4]{2}\right)-2$\\$2 x+\sqrt[4]{2} \cdot x^2-2 \cdot \sqrt[4]{2} \cdot x+\sqrt[4]{2}-2$\)
\($f(x)=\sqrt{12(x-1)}-\sqrt{2(x-1)^2}$\)
\($\frac{d}{d x}\left(\sqrt{12(x-1)}-\sqrt{2(x-1)^2}\right)$\)
\($\sqrt{12(x-1)}-\sqrt{2(x-1)^2}=2 \sqrt{3} \sqrt{x-1}-\sqrt{2}(x-1)$\)
\($\sqrt{12(x-1)}-\sqrt{2(x-1)^2}$\)
\($\sqrt{12(x-1)}=2 \sqrt{3} \sqrt{x-1}$\)
\($\sqrt{2(x-1)^2}=\sqrt{2}(x-1)$\\$=2 \sqrt{3} \sqrt{x-1}-\sqrt{2}(x-1)$\\\)
Values that might result in a fraction's denominator being equal to zero are excluded. Finding these omitted values is crucial for resolving a rational statement because you cannot divide by 0.
To learn more about quotient refer to :
https://brainly.com/question/11418015
#SPJ1
Please answer this. I will give you Brainliest.

Answers
Answer:
A) \(14.9\)
Step-by-step explanation:
\(0.3r-4.9\\\\0.3(66)-4.9\\\\19.8-4.9\\\\14.9\)
Answer:
14.9
Step-by-step explanation:
It's simple. Just replace the r with 66.
Over the past 30 years in the US there has been a strong negative correlation between the number of infant deaths at birth and the number of people over the age 65. Is the fact that people are living longer causing a decrease in infant deaths at birth?
Answers
Yes, the fact that people are living longer is likely causing a decrease in infant deaths at birth in the US. This is because advancements in medical technology and healthcare have allowed for better prenatal care and delivery methods, which have contributed to lower infant mortality rates.
Additionally, as more people live into old age, there is likely more knowledge and experience in caring for newborns, further decreasing the likelihood of infant deaths.
Therefore, the negative correlation between the number of infant deaths at birth and the number of people over the age 65 can be attributed to a combination of factors related to improvements in healthcare and the aging population.
To know more about healthcare, refer to the link:
https://brainly.com/question/17051267#
#SPJ11
Matti is making moonshine in the woods behind his house. He’s
selling the moonshine in two different sized bottles: 0.5 litres
and 0.7 litres. The price he asks for a 0.5 litre bottle is 8€, for
a
Answers
Based on the calculation, it appears that Matti had approximately 94 bottles of 0.5 litres and 11 bottles of 0.7 litres in the last patch of moonshine that he sold.
To solve the problem using the determinant method (Cramer's rule), we need to set up a system of equations based on the given information and then solve for the unknowns, which represent the number of 0.5 litre bottles and 0.7 litre bottles.
Let's denote the number of 0.5 litre bottles as x and the number of 0.7 litre bottles as y.
From the given information, we can set up the following equations:
Equation 1: 0.5x + 0.7y = 16.5 (total volume of moonshine)
Equation 2: 8x + 10y = 246 (total earnings from selling moonshine)
We now have a system of linear equations. To solve it using Cramer's rule, we'll find the determinants of various matrices.
Let's calculate the determinants:
D = determinant of the coefficient matrix
Dx = determinant of the matrix obtained by replacing the x column with the constants
Dy = determinant of the matrix obtained by replacing the y column with the constants
Using Cramer's rule, we can find the values of x and y:
x = Dx / D
y = Dy / D
Now, let's calculate the determinants:
D = (0.5)(10) - (0.7)(8) = -1.6
Dx = (16.5)(10) - (0.7)(246) = 150
Dy = (0.5)(246) - (16.5)(8) = -18
Finally, we can calculate the values of x and y:
x = Dx / D = 150 / (-1.6) = -93.75
y = Dy / D = -18 / (-1.6) = 11.25
However, it doesn't make sense to have negative quantities of bottles. So, we can round the values of x and y to the nearest whole number:
x ≈ -94 (rounded to -94)
y ≈ 11 (rounded to 11)
Therefore, based on the calculation, it appears that Matti had approximately 94 bottles of 0.5 litres and 11 bottles of 0.7 litres in the last patch of moonshine that he sold.
for such more question on litres
https://brainly.com/question/27877215
#SPJ8
Question
Matti is making moonshine in the woods behind his house. He’s selling the moonshine in two different sized bottles: 0.5 litres and 0.7 litres. The price he asks for a 0.5 litre bottle is 8€, for a 0.7 litre bottle 10€. The last patch of moonshine was 16.5 litres, all of which Matti sold. By doing that, he earned 246 euros. How many 0.5 litre bottles and how many 0.7 litre bottles were there? Solve the problem by using the determinant method (a.k.a. Cramer’s rule).
diseases tend to spread according to the exponential growth model. in the early days of aids, the growth factor (i.e. common ratio; growth multiplier) was around 1.9. in 1983, about 1700 people in the u.s. died of aids. if the trend had continued unchecked, how many people would have died from aids in 2005?
Answers
The number of people died from aids in U.S. in 2005 are 2,30,68,96,671
Given, diseases tend to spread according to the exponential growth model.
In the early days of aids, the growth factor (i.e. common ratio; growth multiplier) was around 1.9.
In 1983, about 1700 people in the U.S. died of aids.
we have to find the number of people died from aids in 2005.
Let the exponential function, be
P(x) = AB^x
where, A is the initial population of people died of aids in U.S.
B is the growth factor of aids in U.S.
as, B = 1.9
In 1983, x = 0
P(0) = AB^0
1700 = A
Now, P(x) = 1700(1.9)^x
and the number of years from 1983 to 2005 are, 22 years
The number of people died from aids in 2005 be,
P(22) = 1700(1.9)^22
P(22) = 2,30,68,96,671
So, 2,30,68,96,671 people died from aids in 2005.
Hence, 2,30,68,96,671 people died from aids in 2005.
Learn more about Exponential Functions here https://brainly.com/question/12472697
#SPJ4
Can somebody help me, please

Answers
Answer:
uh I don't even know what this is
Answer: x = 500
Step-by-step explanation:
Use the Pythagorean Theorem
a²+b²=c²
300² + 400² = x²
90000 + 160000 = x²
250000 = x²
√250000 = √x²
500 = x
hope i explained it :)
an article gave the following observations on a maximum concrete pressure (kn/m^2): 33.3 41.8 37.4 40.2 36.7 39.1 36.2 41.8 36.0 35.2 36.7 38.9 35.8 35.2 40.1 using a normal probability plot, we ascertain that it is plausible that this sample was taken from a normal population distribution. calculate an upper confidence bound with confidence level 95% for the population standard deviation of maximum pressure.
Answers
A mean of a normal distribution's upper bound of a 95% confidence interval is 58.11.
What does "confidence interval" mean?This confidence interval would just be constructed using the Z or t distribution depending on the confidence level that was selected and the standard error of the point estimate.The standard error of the point estimate will be used to account for the variation in the important finding for every one of the outcome measures.For the given question,
sample mean μ = 554.4/15 = 36.96standard deviatio σ = 41.8sample size n = 15confidence interval = 95%The confidence bound's upper limit (UCB) is determined as follows:
UCB = μ + z(α/2)×σ/√n
Now, α/2 = (1 - 0.95)/2
α/2 = 0.025
z(α/2) = 1.96 (obtain from t-distribution table for degree of freedom)
Put the values in the formula,
UCB = μ + z(α/2)×σ/√n
UCB = 36.96 + 1.96×41.8/√15
UCB = 58.11
As a result, 58.11 is the upper bound of a 95% confidence interval for the mean of a normal distribution.
To know more about confidence interval, here
brainly.com/question/15712887
#SPJ4
Evaluate 8 - m/n + p2 when m = 8, n = 2, p=7
Answers
Answer:
8-m/n+p^3= 8-8/2+7^2 sub in the numbers for the variables
(8-8)/2+7^2 Exponents
(8-8)/2+49 add the denominators together
(8-8)/60 subtract 8-8
0/60 is the answer (which doesn't seem right to me)
Step-by-step explanation:
Which measures are used in the five-number summary? A. Standard deviation B. Minimum value C. First quartile D. Median
Answers
The minimum value and median are used in the five-number summary.
What is the box-and-whisker plot?A box and whisker plot displays a "box" with its left edge at Q₁, right edge at Q₃, "center" at Q₂ (the median), and "whiskers" at the maximum and minimum.
Given:
A five-number summary.
That means minimum value, lower quartile (Q1), median value (Q2), upper quartile (Q3), and maximum value.
From the given choices:
The minimum value and median are the required measures.
Therefore, the minimum value and median are the required measures.
To learn more about the box-and-whisker plot ;
https://brainly.com/question/2742784
#SPJ1
two stores each have the same number of lawn mowers for sale. the lawn mowers at store a have a median price of $150. the lawn mowers at store b have a median price of $200.
Answers
The median price of all the lawn mowers for sale is $175.
If the two stores have the same number of lawn mowers for sale, then the median price of all the lawn mowers can be found by taking the average of the two median prices, which is:
median price = (150 + 200) / 2 = 175
Therefore, the median price of all the lawn mowers for sale is $175.
However, it is important to note that the median price may not give us a complete picture of the prices of all the lawn mowers at each store. For example, one store could have a wide range of prices for its lawn mowers, with a few very expensive models bringing up the median price, while the other store could have a more consistent range of prices with fewer outliers. Therefore, it would be best to also look at other measures of central tendency, such as the mean or mode, and to examine the entire range of prices at each store before making a decision on where to buy a lawn mower.
Learn more about "median" : https://brainly.com/question/26177250
#SPJ11
Maggie graphed the image of a 90 counterclockwise rotation about vertex A of . Coordinates B and C of are (2, 6) and (4, 3) and coordinates B’ and C’ of it’s image are (–2, 2) and (1, 4). What is the coordinate of vertex A.
Answers
Answer:
free points? ill answer anyway! :)
Step-by-step explanation:
maggie graphed -2-8 so the vertex could be 270 degrees and the B'-2, 2 SO now B' -4 8 and same with C' 3, -8 now instead of C' 1/4! hoped this helped!!
The length of one diagonal of a rhombus is 4 times the length of the other diagonal. Write an expression that represents the perimeter of the rhombus. Let d be the length of the shorter diagonal.
Answers
The expression that represents the perimeter of the rhombus is 2d√17
How to determine the expression that represents the perimeter of the rhombus?
From the question, we have the following parameters that can be used in our computation:
The length of one diagonal of a rhombus is 4 times the length of the other diagonal.
This means that
Length 1 = 4 * Length 2
From the question, we have
Let d be the length of the shorter diagonal.
This means that
Length 1 = 4d
Length 2 = d
The perimeter of the rhombus from the diagonals is calculated as
P = 2√(Length 1² + Length 2²)
Substitute the known values in the above equation, so, we have the following representation
P = 2√((4d)² + d²)
Evaluate the exponents
P = 2√(16d² + d²)
So, we have
P = 2√(17d²)
Evaluate the exponents
P = 2d√17
Hence, the perimeter is 2d√17
Read more about perimeter at
https://brainly.com/question/19819849
#SPJ1