Tres cargas puntuales, q1=5uc,q3=5uc y q2=-2. 0uc, se encuentran en los vértices de un triángulo rectángulo la longitud de los catetos del triángulo es de 10 cm cuál es la fuerza resultante sobre q3
Answers
La fuerza resultante sobre q3 debe calcularse considerando la interacción de las cargas q1, q2 y q3.
How to calculate the resultant force on q3?Para determinar la fuerza resultante sobre q3, debemos calcular la magnitud y la dirección de las fuerzas ejercidas por q1 y q2 sobre q3.
Usando la Ley de Coulomb, podemos calcular la fuerza entre dos cargas puntuales utilizando la fórmula: F = k * (|q1| * |q2|) / r^2, donde k es la constante de Coulomb, |q1| y |q2| son los valores absolutos de las cargas, y r es la distancia entre las cargas.
Dado que las cargas q1 y q3 son iguales, y q2 tiene una carga negativa, las fuerzas ejercidas por q1 y q2 en q3 tendrán direcciones opuestas. Debido a la simetría del triángulo rectángulo, las fuerzas tendrán componentes horizontales y verticales iguales en magnitud.
La magnitud de la fuerza resultante sobre q3 se calcula sumando las magnitudes de las fuerzas ejercidas por q1 y q2. La dirección de la fuerza resultante será la misma que la de las fuerzas individuales ejercidas por q1 y q2.
Por lo tanto, para calcular la fuerza resultante sobre q3, debemos encontrar la magnitud de la fuerza ejercida por q1 y la magnitud de la fuerza ejercida por q2, y luego sumarlas. La dirección será la misma que las fuerzas individuales.
Learn more about determinar
brainly.com/question/30457159
#SPJ11
Related Questions
If a polynomial function, f(x), with rational coefficients has roots 3 and startroot 7 endroot, what must also be a root of f(x)?
Answers
The conjugate which is 3 - √7 is also a root of f(x).
What is the root of a polynomial function?The root of a polynomial function f(x) is the value of x for which f(x) = 0.
Now if a polynomial function has a root x = a + √b then the conjugate of x which is x' = a - √b is also a root of the function, f(x).
What must also be a root of f(x)?
Given that the polynomial function, f(x), with rational coefficients has roots
3 + √7, then by the above, the conjugate which is 3 - √7 is also a root of f(x).
So, 3 - √7 is also a root of f(x).
Learn more about root of a polynomial function here:
https://brainly.com/question/2833285
#SPJ1
A pallet of floor tiles contains 60 cases of tiles, and the yard has 10 complete pallets of tile. If you remove 180 cases for one customer how many cases of tiles will be remaining in the yard?
Answers
Total cases = total pallets x cases per pallet
Total cases = 60 x 10 = 600 cases
600 cases - 180 cases = 420 cases left
Answer: 420 cases
PLEASEEEEE I NEED HELP WITH THIS!!
Solve for x.
5
6X 30
7 1
X+ x =
5*= -52
x =
(Type an integer or a simplified fraction.)

Answers
Answer:
x = 60
Step-by-step explanation:
Given: j(x) = x2 - 2x + 1
Which set of values represents the range of the function for the domain {0, 1, 5}?

Answers
Answer:
{1, 0, 16}
Step-by-step explanation:
given..
j(x) = x^2-2x+1
put all given values of domain (1,0 and 5 ) in the equation..
the values you get are range of the function
Answer: 1
Step-by-step explanation
0(2)-2(0)+1=0+0+1= 1
1(1)-(2)(1)+1=1-2+1= 1
(5)(2)-(2)(5)+1=10-10+1= 1
Jim, Carla and Tomy are members of the same family. Carla is 5 years older than Jim. Tomy is 6 years older than Carla. The sum of their three ages is 31 years. How old is each one them?
Answers
We are given these three people age below:
Jim's ageCarla's ageTomy's ageWe define the age of Jim as any variable, because the problem doesn't give any specific age. I will define Jim's age as x.
Jim's age = xNext, Carla is 5 years older than Jim. That means if Carla is 5 years older, her age would be x+5.
Carla's age = x+5Then Tomy is 6 years older than Carla. That means the age would be 6+(x+5).
Tomy's age = 6+(x+5)The sum of their three ages is 31 years old. That means we add all these ages and equal to 31.
\( \large{x + x + 5 + 6 + x + 5 = 31}\)
Combine like terms and solve for x.
\( \large{3x + 16 = 31} \\ \large{3x = 31 - 16} \\ \large{3x = 15} \\ \large{x = 5}\)
Then we substitute the value of x in ages to find these three people ages.
Jim's age = x = 5Carla's age = x+5 = 5+5 = 10Tomy's age = 6+(x+5) = 6+(5+5) = 6+10 = 16.Answer
Jim's age = 5Carla's age = 10Tomy's age = 16Solve by completing the square:
x^2 + 2x - 3 =0
a. - 3 or 1
b. X-3 or -1
C. - 3 or -1
d. 2-3 or 1
Please select the best answer from the choices provided
Answers
Answer:
a
Step-by-step explanation:
Given
x² + 2x - 3 = 0 ( add 3 to both sides )
x² + 2x = 3
To complete the square
add ( half the coefficient of the x- term )² to both sides
x² + 2(1)x + 1 = 3 + 1
(x + 1)² = 4 ( take the square root of both sides )
x + 1 = ± \(\sqrt{4}\) = ± 2 ( subtract 1 from both sides )
x = - 1 ± 2
Thus
x = - 1 - 2 = - 3
x = - 1 + 2 = 1
The weights of cars passing over a bridge have a mean of 3,550 pounds and standard deviation of 870 pounds.Assume that the weights of the cars passing over the bridge are normally distributed. What is z-score corresponding to a car that weighs 2800 pounds?
Answers
The z-score corresponding to a car that weighs 2800 pounds is approximately -0.86.
We have,
We can find the z-score corresponding to a car that weighs 2800 pounds using the formula:
z = (x - μ) / σ
where x is the weight of the car, μ is the mean weight, and σ is the standard deviation.
Substituting the given values, we get:
z = (2800 - 3550) / 870
z = -0.86
Therefore,
The z-score corresponding to a car that weighs 2800 pounds is approximately -0.86.
Learn more about z-score here:
https://brainly.com/question/15016913
#SPJ1
What is the midpoint of FB

Answers
Point L is the midpoint
The midpoint is halfway between the two points. In this case, Point F and Point B are 10 units away from each other. The midpoint is the distance between the points (10) divided by 2.
Addison worked 11 more hours this week than last week. In total, she worked 65 hours this week and last week. Using the equation 2h + 11 = 65, how many hours (h) did Addison work last week?
Answers
Answer:
27
Step-by-step explanation:
2h+11=65
2h= 65-11
2h=54
then divide both side by two to find h
Im stuck on this problem. 25 points for the help!

Answers
Answer:
Step-by-step explanation:
First we can determine that this is a special 45-45-90 triangle, since the two legs are congruent, meaning the two unknown angles are congruent as well:
180 = 90 + 2(theta)
theta = 45
Knowing this, we can remember that the hypotenuse of this special triangle is equal to the leg*sqrt(2).
This means that 1 = x(sqrt(2)).
\(x=\frac{1}{\sqrt{2} }\)
Hope this helps!
John orders 25 prints from a photo store for $13.00.
What is the cost per print?
Answers
Answer:
$0.52 or 52 cents
Step-by-step explanation:
Ratios:
\(\frac{25}{13} =\frac{1}{x} \\\\25x=13\\x=0.52\)
If the mug cost $6 last year and the price increased by 25%, how much did the mug cost this year?
Answers
Answer:7.5
Step-by-step explanation:
6*0.25=7.5
Anyone know this one ?
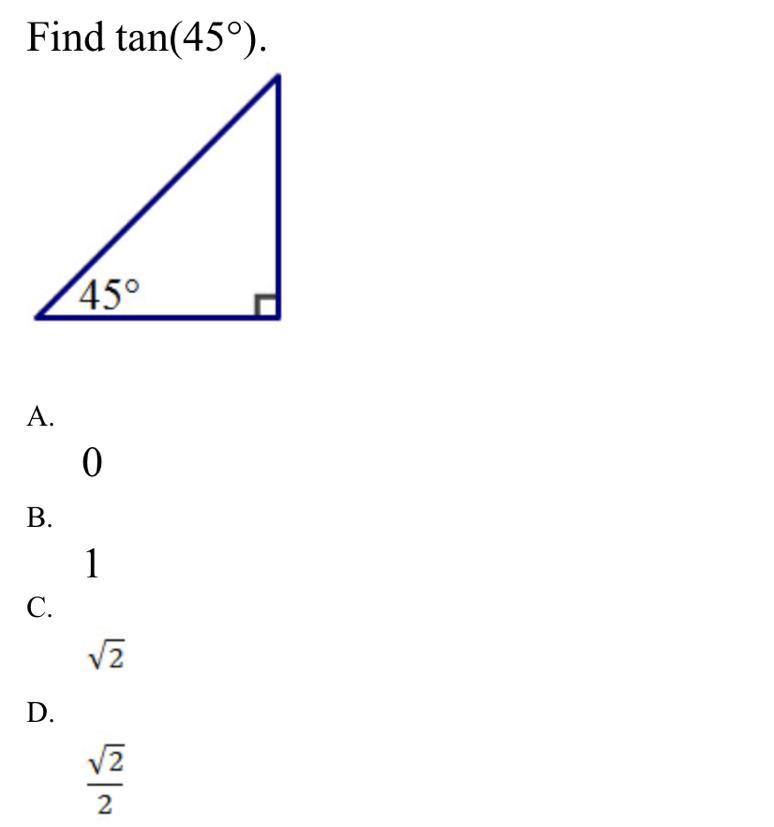
Answers
tan is (opposite)/(adjacent). In the triangle you can see that the opposite and adjacent sides are the same length, because it's a 45-45-90 triangle. So, something divided by the same thing will give 1.
Dne leg of a right triangle is seven more than the other leg. The hypotenuse is eight more than the shorter leg. Find the length of the hypothenuse.
Answers
In a right triangle, the length of one leg is seven more than the other leg, and the hypotenuse is eight more than the shorter leg. By applying the Pythagorean theorem, we can determine the length of the hypotenuse, which is found to be 13 units.
Let's denote the shorter leg of the right triangle as x.
According to the given information, the longer leg is seven more than the shorter leg, so its length is x + 7.
The hypotenuse is eight more than the shorter leg, so its length is x + 8.
We can use the Pythagorean theorem to relate the lengths of the legs and the hypotenuse:
x^2 + (x + 7)^2 = (x + 8)^2
Expanding the equation:
x^2 + x^2 + 14x + 49 = x^2 + 16x + 64
Simplifying the equation:
2x^2 + 14x + 49 = x^2 + 16x + 64
Rearranging terms:
x^2 - 2x - 15 = 0
Now, we can factor the quadratic equation:
(x - 5)(x + 3) = 0
Setting each factor equal to zero:
x - 5 = 0 --> x = 5
x + 3 = 0 --> x = -3
Since lengths cannot be negative, we discard x = -3.
Therefore, the length of the shorter leg is x = 5, the length of the longer leg is x + 7 = 12, and the length of the hypotenuse is x + 8 = 13.
So, the length of the hypotenuse is 13.
Learn more about hypotenuse here:
https://brainly.com/question/16893462
#SPJ11
zelda has 8 rabbits with which to start an animal the rabbit population doubleseach month, in how many months will the rabbit population be 5,800 answers
Answers
It will take about 9.5 months (or 10 months rounded up) for the rabbit population to reach 5,800.
How to find the rabbit population?Let's use the formula for exponential growth to solve this problem:
N = N0 * 2^(t/k)
Where:
N0 = initial population (8 rabbits)
N = final population (5,800 rabbits)
k = doubling time (1 month)
t = time in months (what we're trying to find)
Substituting the values we have:
5,800 = 8 * 2^(t/1)
Dividing both sides by 8:
725 = 2^(t/1)
Taking the logarithm of both sides (base 2):
log2(725) = t/1
t = log2(725) ≈ 9.515
So it will take about 9.5 months (or 10 months rounded up) for the rabbit population to reach 5,800.
Learn more about logarithm
brainly.com/question/30226560
#SPJ11
(Pls Help ASAP)( If you dont know dont answer)

Answers
Answer:
Consistent, Inconsistent, Dependent, Independent
Step-by-step explanation:
A system of equations that has at least one solution is classified as Consistent.
A system of equations that has at least one and only one solution is classified as Inconsistent.
The system of equations in the graph is Dependent and Independent.
Use the rules of differentiation to to find the derivatives of the functions: (a) f(x) = 3x^2+4/x^2+2
(b) f(x) = (x2 - 7x)^12
(c) f(x) = x^4√6x+5
Answers
The solution to the given question is given below:(a) f(x) = 3x^2+4/x^2+2To differentiate the given function, we will use the quotient rule of differentiation.
which is given by,(f(x)/g(x))'=[f'(x)g(x)-f(x)g'(x)]/[g(x)]2Now, putting the given values into the formula, we get,f(x) = 3x2+4/x2+2Let f(x) = 3x2+4 and g(x) = x2+2Now,f'(x) = d/dx[3x2+4] = 6xg'(x) = d/dx[x2+2] = 2xAfter substituting all the values in the quotient rule, we get,(f(x)/g(x))'=(6x(x2+2)-2x(3x2+4))/(x2+2)2=(-6x^3-8x+12x^3+16x)/[x^4+4x^2+4] = (6x^3+8x)/[x^4+4x^2+4]Hence, f'(x) = (6x^3+8x)/[x^4+4x^2+4].Therefore, the required derivative of the given function is (6x^3+8x)/[x^4+4x^2+4].(b) f(x) = (x2 - 7x)12To differentiate the given function, we will use the chain rule of differentiation which is given by, d/dx[f(g(x))] = f'(g(x)).g'(x)Now, putting the given values into the formula, we get,Let f(x) = x^12 and g(x) = x2-7xThen,f'(x) = 12x^11g'(x) = d/dx[x2-7x] = 2x-7After substituting all the values in the chain rule, we get,d/dx[f(g(x))] = f'(g(x)).g'(x) = 12(x2-7x)11.(2x-7)Therefore, the required derivative of the given function is 12(x2-7x)11.(2x-7).(c) f(x) = x^4√6x+5To differentiate the given function, we will use the product rule of differentiation which is given by, (fg)' = f'g + fg'Now, putting the given values into the formula, we get,Let f(x) = x^4 and g(x) = √6x+5Then,f'(x) = d/dx[x4] = 4x3g'(x) = d/dx[√6x+5] = 3/√6x+5After substituting all the values in the product rule, we get,(fg)' = f'g + fg' = (4x3).(√6x+5) + (x^4).(3/√6x+5)Hence, f'(x) = (4x3).(√6x+5) + (x^4).(3/√6x+5).Therefore, the required derivative of the given function is (4x3).(√6x+5) + (x^4).(3/√6x+5).
To know more about differentiation visit:
https://brainly.com/question/13958985
#SPJ11
The derivatives of the functions of the differentiation of the given functions has been calculated.
(a) The rule of differentiation applied to
f(x) = 3x²+4/x²+2 is as follows:
f'(x) = [12x(x²+2)-(6x)(4)] / [(x²+2)²]
=> f'(x) = [12x³-24x] / [(x²+2)²]
=> f'(x) = 12x(1-x²)/[(x²+2)²].
(b) The rule of differentiation applied to f(x) = (x² - 7x)^12 is as follows:
f'(x) = 12(x²-7x)^11(2x-7).
We apply the chain rule, which is the following:
[f(g(x))]' = f'(g(x)) * g'(x).(c)
The rule of differentiation applied to f(x) = x⁴√(6x+5) is as follows:
f'(x) = 4x³ * (6x+5)¹∕² + x⁴ * 1/2(6x+5)^-1/2 * 6
=> f'(x) = [24x³(6x+5) + 3x⁴(6)]/[2(6x+5)¹∕²]
=> f'(x) = [3x³(8x²+15)]/[(6x+5)¹∕²].
Thus, the differentiation of the given functions has been calculated.
To know more about differentiation, visit:
https://brainly.com/question/13958985
#SPJ11
Help me quick please solve in inequality please

Answers
Answer:
B
i don't know how to explain what i did correctly but the answer is B
Answer:
D.
Step-by-step explanation:
x + 3 is 3 more laps
≥ 12 means at least 12.
Rita tutors history. For each hour that she tutors, she earns 40 dollars. her earning, E (in dollars), after tutoring for h hours is given by the following function.E (h) =40hHow much does Rita earn if she tutors for 2 hours?? dollars
Answers
Earning per hour E(h) = 40h
h = number of hours
Therefore, for 2 hours
Earning E(h) = 40h
= 40 x 2
= 80 dollars
Please help me answer this question

Answers
Answer:
(x-4) (x-4)
Step-by-step explanation:
-4 + -4 = -8
-4 x -4 = 16
Eric has a bag of carrots that weighs 3 pounds. He separates the carrots equally into 10 containers. How many pounds are in each container?
Answers
Answer:
3/10 pounds
Step-by-step explanation:
Distribute 3 pounds equally into 10 containers so it is 3/10 pounds in each container.
(I’m having trouble with this question, it would be greatly appreciated if I could have some help, thank you)
What is the equation of a line that is parallel to – 2x + 3y = -6 and passes through the point (-2, 0)?
Answers
Answer:
y = 2/3x + 4/3
Step-by-step explanation:
you need to know the slope of the line -2x + 3y = -6 because parallel lines have the same slopes
let's put the equation in y=mx+b format (slope-intercept format)
-2x + 3y = -6
add 2x to each side to get:
3y = 2x - 6
divide each side by 3 to get:
y = 2/3x - 2
the equation now shows us the slope is 2/3 and the y-intercept is (0,-2)
now we use y=mx+b again and use the point (-2,0) and the m=2/3 to get the y-intercept ('b' value) of the equation that is parallel:
0 = 2/3(-2) + b
0 = -4/3 + b
b = 4/3
equation would be:
y = 2/3x + 4/3
Sixty percent of the profit was used to pay the investors. If $15,000 was not used to pay the investors, what was the
total amount of profit?
please please help i have a pretest that’s due in 40 mins i will mark anyone as 5 stars
Answers
For the expression (a 0 3(a - b) b) = (1 0 3 1) (a 0 0 b) (1 0 -3 1) Use the factorization 'A=PDP-1'to compute 'Ak' where 'k' represents an arbitrary positive integer.
Answers
Given the matrix expression A = (a 0 3(a-b) b) = (1 0 3 1) (a 0 0 b) (1 0 -3 1), we want to compute the matrix power Ak using the factorization A = PDP^-1.
First, we need to find the matrices P and D. The matrix D is a diagonal matrix consisting of the eigenvalues of A, which are a, b+3a, and b-3a. The matrix P is the matrix whose columns are the eigenvectors of A, which can be found by solving the system (A - λI)x = 0 for each eigenvalue λ.
Solving for each eigenvalue, we get λ1 = a with eigenvector (0,1), λ2 = b+3a with eigenvector (-3,1), and λ3 = b-3a with eigenvector (1,1). Thus, we have:
D = (a 0 0
0 b+3a 0
0 0 b-3a)
P = (0 -3 1
1 1 1
0 0 1)
To compute Ak, we can use the formula A^k = PD^kP^-1. Since D is a diagonal matrix, we can easily compute D^k by raising each diagonal entry to the power of k. Thus, we get:
D^k = (a^k 0 0
0 (b+3a)^k 0
0 0 (b-3a)^k)
Multiplying out the matrices P and P^-1, we get:
P^-1 = (1/3 -1/3 0
-1/3 2/3 -1/3
0 -1/3 1/3)
P^-1AP = D
Multiplying both sides by P^-1, we get:
A = PDP^-1
Now, substituting D^k into the formula A^k = PD^kP^-1, we get:
A^k = P D^k P^-1
Substituting the matrices P, P^-1, and D^k, we get the expression for Ak as:
Ak = (1/3)((b+3a)^k - (b-3a)^k) (1 -3(b-3a)^k/(b+3a)^k - 3(b+3a)^k/(b-3a)^k 1) (a 0 0 b)
Therefore, we have the expression for Ak.
Learn more about expression here:
https://brainly.com/question/14083225
#SPJ11
Al dividir "D" entre "d" se obtuvo 12 de
cociente y 8 de residuo. Si: D + d = 203.
Hallar: D
Answers
El valor que satisface D es 188.
El modelo matemático será así:
D/d = 12(resto 8)
si escribimos 8 como resto de D, entonces:
(D-8) /d=12
D-8= 12d o se puede escribir D= 12d+8
luego sustituya D= 12d+8 por D+d= 203
D+d= 203
(12d +8) +d= 203
13d= 203-8
13d= 195
re=15
sustituir d=15 en D+d= 203
D+d= 203
D+15=203
D=203-15
D=188
Sobre el modelo matemáticoEl modelo matemático es una forma de interpretación humana al traducir o formular problemas existentes en forma matemática, de modo que el problema pueda resolverse utilizando las matemáticas.
El uso principal de los modelos matemáticos es ayudar a las personas a comprender los problemas y simplificarlos para que puedan resolverse.
, los siguientes son algunos de los usos que se obtienen al utilizar un modelo matemático, a saber:
Agrega velocidad, claridad y poder de ideas en un período de tiempo relativamente corto. La descripción del problema ocupa un lugar central. Obtener una comprensión o claridad del mecanismo en el problema. Se puede utilizar para predecir eventos que surgirán de un fenómeno o su expansión. Como base para la planificación y el control en la formulación de políticas, entre otros.Obtenga más información sobre el modelo matemático en
https://brainly.com/question/30517381
#SPJ1
What is the equation, in slope-intercept form, of the line that is perpendicular to the line y-4= -2/3 (x-6) and passes through the point (-2, -2)?
Oy=-2/3x-10
Oy=-2/3x+10
Oy=x3/2x-1
O y=3/2x+1

Answers
Answer:
The answer is option D.
Equation of a line is y = mx + c
m = slope
c = intercept on y axis
y-4= -2/3 (x-6)
y = -2/3x + 4 + 4
y = -2/3x + 8
From the above equation
m= -2/3
Since the lines are perpendicular the slope of the line is the negative inverse of the original line.
so m = 3/2
Equation of the line using point (-2 , -2) is
y + 2 = 3/2(x+2)
y = 3/2x + 3 - 2
y = 3/2x + 1
That's the last option
Hope this helps
The linear equation with the given characteristics is given by:
\(y = \frac{3}{2}x + 1\)
What is the equation of a line in slope-intercept form?It is given by:
y = mx + b.
In which:
m is the slope.b is the y-intercept.When two lines are perpendicular, the multiplication of their slopes is -1, hence:
\(-\frac{2}{3}m = -1\)
\(2m = 3\)
\(m = \frac{3}{2}\)
Then:
\(y = \frac{3}{2}x + b\)
It passes through the point (-2, -2), hence:
\(-2 = \frac{3}{2}(-2) + b\)
\(-3 + b = -2\)
\(b = 1\)
Hence, the equation is:
\(y = \frac{3}{2}x + 1\)
More can be learned about linear equations at https://brainly.com/question/24808124
vocab word for this definetion
Answers
Answer:
whats the definition?
Step-by-step explanation:
I having a hard time figuring this out.

Answers
Answer:
33
Step-by-step explanation:
Start by adding the 3 to the other side (2/3x=22)
Then, you divide 2/3 to cancel it out. To do that, multiply 22 by 3/2 which equals to 33.
Answer:
2/3x - 3 = 19
We first isolate the variable and solve for x, (we get rid of any constants first in the process)
2/3x - 3 = 19 the three is the constant so we get rid of it by adding three to both sides.
2/3x - 3 = 19
+3 +3
2/3x = 22
Now we divide by 2/3 on both sides
X = 33
. How many days will it take for $9500 to earn $800 at 8.25% p.a.?
Answers
It will take approximately 39.532 days for $9500 to earn $800 at an annual interest rate of 8.25%.
To find the number of days it will take for $9500 to earn $800 at an annual interest rate of 8.25%, we need to use the formula for simple interest:
Interest = Principal * Rate * Time
In this case, we are given the interest ($800), the principal ($9500), and the annual interest rate (8.25%). We need to solve for time.
Let's denote the time in years as "t". Since we're looking for the number of days, we'll convert the time to a fraction of a year by dividing by 365 (assuming a standard 365-day year).
$800 = $9500 * 0.0825 * (t / 365)
Simplifying the equation:
800 = 9500 * 0.0825 * (t / 365)
Divide both sides by (9500 * 0.0825):
800 / (9500 * 0.0825) = t / 365
Simplify the left side:
800 / (9500 * 0.0825) ≈ 0.1083
Now, solve for t by multiplying both sides by 365:
0.1083 * 365 ≈ t
t ≈ 39.532
Therefore, it will take approximately 39.532 days for $9500 to earn $800 at an annual interest rate of 8.25%.
for such more question on annual interest rate
https://brainly.com/question/29451175
#SPJ8
For n sided die (1, 2, ... n)
what is the expected number of times of rolling 2 if you roll k times?
Answers
The expected number of times of rolling 2 for n sided die (1, 2, ... n) if you roll k times is given by the following solution:The probability of rolling 2 on any roll is 1/n, and the probability of not rolling 2 on any roll is (n - 1)/n.
The number of times 2 is rolled in k rolls is a binomial random variable with parameters k and 1/n.The expected value of a binomial random variable with parameters n and p is np.
So the expected number of times 2 is rolled in k rolls is k(1/n). Therefore, the expected number of times of rolling 2 if you roll k times for n sided die (1, 2, ... n) is k/n.In summary, for an n sided die (1, 2, ... n), if you roll it k times, the expected number of times you will get a 2 is k/n.
To know more about number visit:
https://brainly.com/question/3589540
#SPJ11