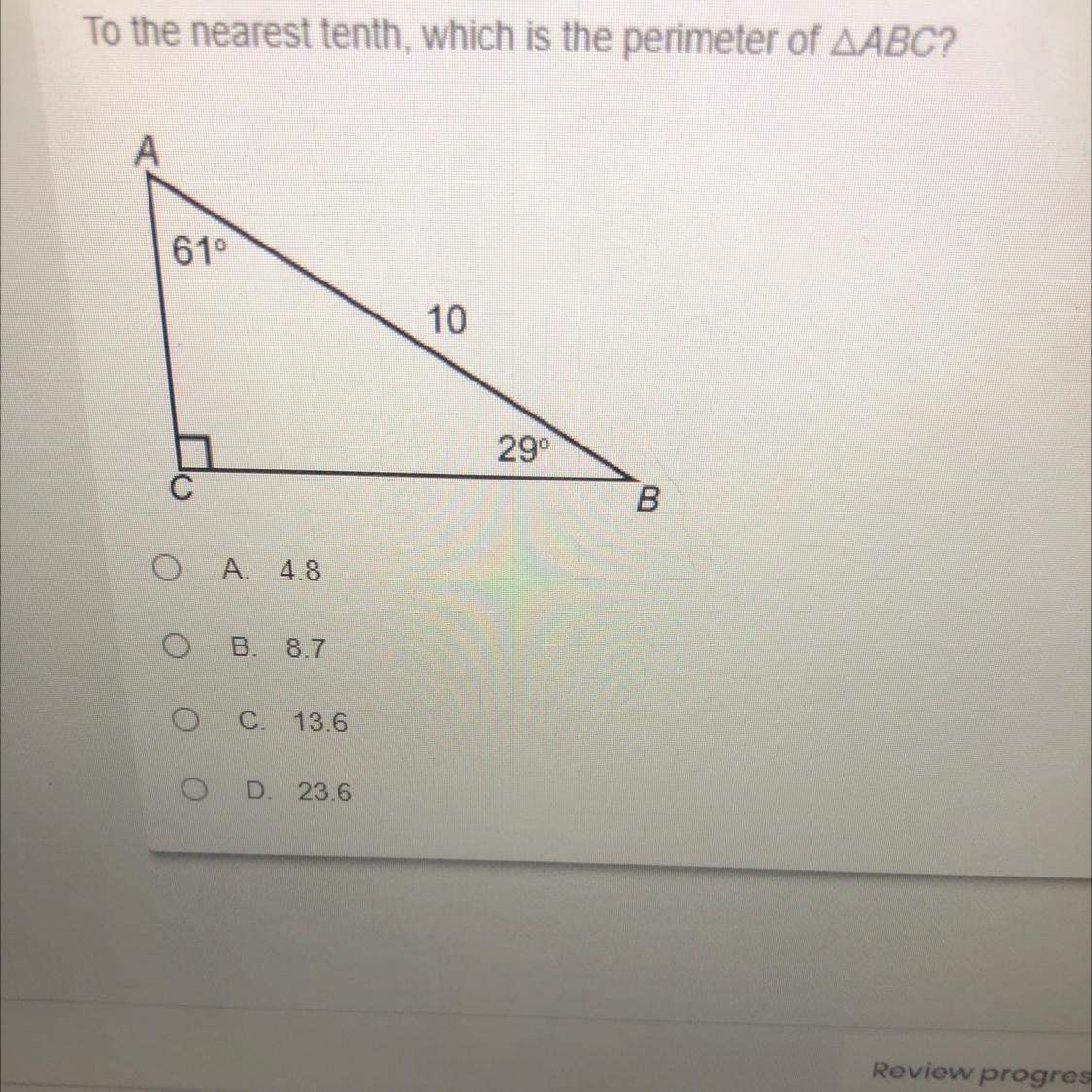
Answers
First let's calculate the sides opposite the angles.
For this we will use the expression for the sine.
In a right angled triangle, the sine of an angle is:
The length of the side opposite the angle divided by the length of the hypotenuse.
The abbreviation is sin
sin θ = opposite / hypotenuse
\(\begin{gathered} AB=h\cdot\sin (29) \\ AB=4.84 \\ \\ CB=h\cdot\sin (61) \\ CB=8.74 \end{gathered}\)The perimeter of a triangle is simply the sum of its three sides.
\(\begin{gathered} P=10+8.74+4.84 \\ P=23.6 \end{gathered}\)The perimeter would be 23.6
Related Questions
Nicole is making a cake that uses 3/4 cup of flour and 1 and 1/8 teaspoons if nicole uses 1 cup of flour how much salt would she need
Answers
Answer:
1.5 teaspoons
Step-by-step explanation:
1/(3/4)
=4/3
9/8*4/3
=1.5 teaspoons
PLS GIVE BRAINLIEST
36,802,277 round of to the nearest millions
Answers
Answer:
37 million
Step-by-step explanation:
What is the cube of 8?
O A. 2
O B. 64
C.53
O D. 24
Answers
Answer:
for my answer i got 512 but it is not one of the answer choices
Step-by-step explanation:
plisss helppppppppppñp

Answers
Answer:
The value of x is 37.36
Step-by-step explanation:
The given triangle is a right-angled triangle where
Base = 25
Angle = 48°
Hypotenuse = x
As the triangle is a right angled triangle, trigonometric ratios can be used to find the missing value. We can use a ratio which uses base and hypotenuse.
\(cos\ 48 = \frac{base}{hypotenuse}\\cos\ 48 = \frac{25}{x}\\0.6691 = \frac{25}{x}\\x = \frac{25}{0.6691}\\x = 37.36\)
Hence ,
The value of x is 37.36
EastLake Middle School is participating in the SDSU Compact for Success field trip. One-fourth of all the students plan on attending. Of those students, two-fourths turned in their permission slips and will be allowed to participate.
Answers
Answer:
3/4
Step-by-step explanation:
1/4+2/4=3/4
3/4 of the students are attending
1/4 of the students are not attending
Kelsey deposited $3,600 in a bank account with annual interest rate 4.25%. How much interest was earned in 5 years?
Answers
Answer:
in 1year =4.25%in 5year=xthen 1=4.25%5=x then cross x=4.25%*5=21.25%Answer:
$765
Step-by-step explanation:
If an amount of money, P, called the principal, is invested for a period of t years at an annual interest rate r, the amount of interest, I, earned is given by
I =Prt where
I =interest
P =principal
r =rate
t =time
The following information is given.
Prt=$3,600=4.25%=5 years
Substituting the given information into the simple interest formula and solving for I gives
I =Prt
I =(3,600)(0.0425)(5)
=765
The amount of interest Kelsey earned in 5 years was $765.
Area of composite shapes ?
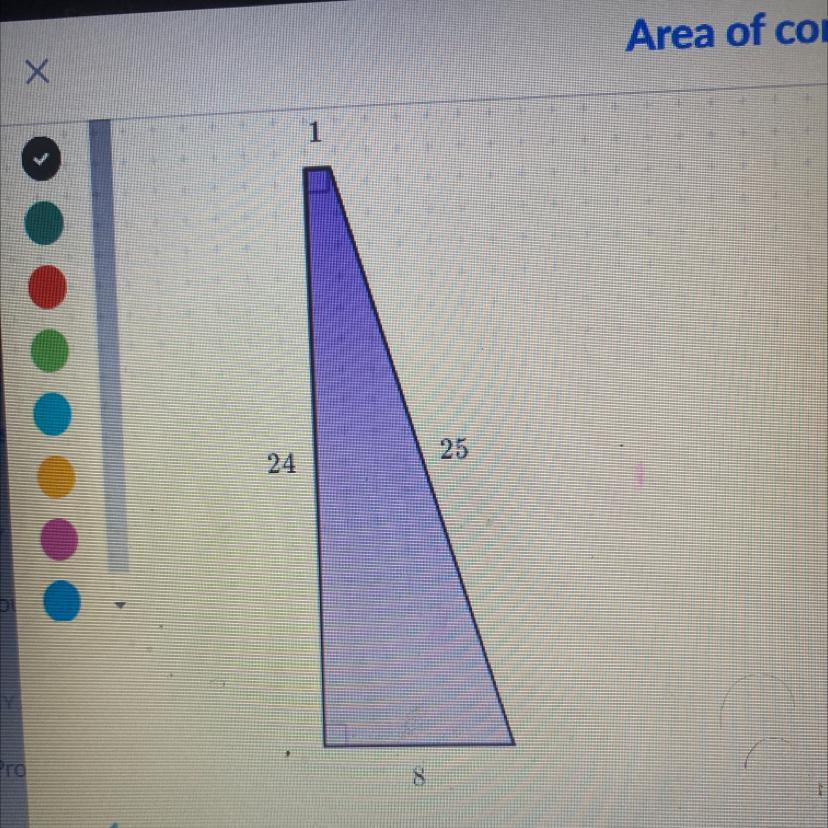
Answers
Answer: 58
Step-by-step explanation: you add them all together
Its 108 the other answer is the perimeter not the area.
Please tell me the answer and how to do it.

Answers
Answer:
there is no constant rate
Step-by-step explanation:
at first i thought it was 25 cents for each, but once i saw the last 3, it broke the rate.
The price of a television was increased from $200 to $250. By what percentage was the price of the television increased
Answers
Answer:
20%
Step-by-step explanation:
cuz quick meths
The measure of one small angles of a right triangle is 45 less than twice the measure of the other small angle. Find the measure of both angles
Answers
Answer:
x + x - 45 = 90
2x - 45 = 90
2x = 135
x = 67.5, so x - 45 = 22.5
The other two angles measure 22.5° and 67.5°.
Pls help i need to get this done or i will get grounded for a week

Answers
Answer: the answer is 3
Step-by-step explanation:
Isolate the x so in other words do the opposite, then you have your answer.
Answer:
D
Step-by-step explanation:
BRUH ALL IT SAYS IS "IT HAS ADDITION" HOW CAN YOU NOT SEE THAT I-
A baseball player had batting average of 0.298 what the probability of him getting exactly 4 out of 10 times he was up at bat
Answers
The probability of the baseball player getting exactly 4 hits out of 10 times at bat is approximately 0.161, or 16.1%.
To calculate the probability of a baseball player getting exactly 4 hits out of 10 times he was up at bat, we need to use the binomial probability formula.
The binomial probability formula is given by:P(X = k) = C(n, k) * p^k * (1 - p)^(n - k)
Where:
P(X = k) is the probability of getting exactly k hits
n is the total number of trials (in this case, the player's 10 times at bat)
k is the number of successful trials (in this case, 4 hits)
p is the probability of success in a single trial (in this case, the player's batting average, 0.298)
(1 - p) is the probability of failure in a single trial
Plugging in the values:
P(X = 4) = C(10, 4) * (0.298)^4 * (1 - 0.298)^(10 - 4)
Using the combination formula C(n, k) = n! / (k! * (n - k)!):
P(X = 4) = 10! / (4! * (10 - 4)!) * (0.298)^4 * (1 - 0.298)^(10 - 4)
Calculating the values:
P(X = 4) ≈ 0.161
For more such questions on probability
https://brainly.com/question/1834572
#SPJ8
Find the area of a circle and use 3.14 for pi

Answers
The area of the shaded region of a circle with a 100 degree angle and a radius of 3cm, using pi=3.14, is approximately 25.64 square centimeters.
To find the area of the shaded region of a circle, we need to subtract the area of the sector formed by the shaded region from the area of the whole circle.
The area of the whole circle is given by
A = πr²
where A is the area of the circle, r is the radius of the circle, and π is a mathematical constant approximately equal to 3.14 (as given in the question).
Substituting the given values, we get
A = π(3cm)²
A = 28.26 cm² (rounded to two decimal places)
Now, let's find the area of the sector formed by the shaded region.
The angle of the sector is given as 100 degrees. To find the area of the sector, we need to use the formula:
A = (θ/360)πr²
where θ is the angle in degrees, r is the radius of the circle, and π is again approximately equal to 3.14.
Substituting the given values, we get
A = (100/360)π(3cm)²
A = 2.62 cm² (rounded to two decimal places)
Finally, we can find the area of the shaded region by subtracting the area of the sector from the area of the whole circle
Shaded area = Area of circle - Area of sector
Shaded area = 28.26 cm² - 2.62 cm²
Shaded area = 25.64 cm² (rounded to two decimal places)
Therefore, the area of the shaded region of the circle is approximately 25.64 square centimeters.
To know more about Area of Circle:
https://brainly.com/question/28642423
#SPJ1
--The given question is incomplete, the complete question is given
" Find the area of a shaded region of circle and use 3.14 for pi "--
Black & Decker Manufacturing sold a set of saws to True Value Hardware. The list price was $3,800. Black & Decker offered a chain discount of 8/3/1. The net price of the saws is:
Answers
The net price of the saws that Black & Decker Manufacturing sold to True Value Hardware on a chain discount of 8/3/1 is $3,357.21.
What is a chain discount?A chain discount refers to a type of discount offered to customers, which is sequentially applied to the list price to arrive at the net price.
Chain discounts involve a series of trade discounts applied in sequence.
Data and Calculations:List price = $3,800
Chain discount = 8/3/1
First net price = $3,496 ($3,800 x 1 - 8%)
Second net price = $3,391.12 ($3,496 x 1 - 3%)
Third net price = $3,357.21 ($3,391.12 x 1 - 1%)
Thus, the net price based on a chain discount of 8/3/1 is $3,357.21.
Learn more about chain discounts at https://brainly.com/question/1515915
#SPJ1
7.
If one United States dollar is worth $6.46 in yen (Chinese currency) in Euro money,
how much is $100 in Yen worth in United States money, to the nearest cent?
Answers
Answer:
$15.48
Explanation:
100 ÷ 6.46 = 15.479876
The regular price of a color TV is $585.83. During a sale, Hill TV is selling the TV for $526.77. Determine the percent decrease in the price of the TV.
Answers
The actual price of the TV is $ 566.37. During a sale, it was sold at $ 502.21. 11.3282% decrease in the price of the TV.
First, we need to the difference in the price.
Let us call the actual price M.R.P and the value it was sold for as S.P
SO we have M.R.P = $ 566.37 and S,P = $ 502.21. THe difference D = M.R.P -S.P = $566.37-$502.21 = $64.16
To find the percent decrease will have to compare the difference with M.R.P and multiply it by a hundred so we get,
D% = (D/M.R.P)x 100 = 64.16/566.37 x100 = 11.3282 %.
Discount pricing is a type of promotional pricing strategy that involves lowering the original price of a product or service with the goal of increasing traffic, moving inventory, and increasing sales. Consumers are attracted to low prices because they want to feel they are getting a good deal.
The difference between what a consumer is willing to pay for a service and the market price. The potential price of Rs.250 and the actual price he considers is Rs.200.
Learn more about the actual price at
https://brainly.com/question/19104371
#SPJ1
1. The graph of a certain geometric sequence can be described as a curve that is decreasing from left to right. Which sequence would have a similar graph?
A {1,1/3,1/9,1,27…}
B{1/16,1/8,1/4,1/2,..,}
Answers
The sequence A, 1, 1/3, 1/9, 1/27 shows the similar graph decreasing from left to right. Option a is correct.
Geometric progression abbreviated as GP is type of sequence and series that has common and equal ratio between preceding values in series.
Here,
The only geometric sequence seems from observation having decreasing from left to right, that implies the curve is also decreasing from left to right is 1, 1/3, 1/9, 1/27, having common ratio of 1/3 with preceding values.
Thus, the sequence 1, 1/3, 1/9, 1/27 shows the similar graph decreasing from left to right which can be described as a curve that is decreasing from left to right.
To learn more about geometric progression refer here:
brainly.com/question/4853032
#SPJ9
The total amount of candy sold at Cassandra's Candy Corner can be represented by the function C(x) = 4x3 + 10x2 + 54x + 520, where x represents the number of years since the store opened. The amount of types of candy can be modeled by the linear function T(x) = 2x + 10. Which expression represents the amount of candy sold each year per type at Cassandra's Candy Corner?
2x^2 – 5x + 52
2x^2 + 5x + 52
4x^3 + 10x^2 + 52x + 510
4x^3 + 10x^2 + 56x + 530
Answers
Using polynomial division, it is found that the expression that represents the amount of candy sold each year per type at Cassandra's Candy Corner is:
\(2x^2 - 5x + 52\)
The amount of candy sold per type is given by the following division:
\(\frac{C(x)}{T(x)} = \frac{4x^3 + 10x^2 + 54x + 520}{2x + 10}\)
The denominator can be written as:
\(2x + 10 = 2(x + 5)\)
At the numerator, to see if we can simplify, we verify if x = -5 is a factor:
\(C(-5) = 4(-5)^3 + 10(-5)^2 + 54(-5) + 520 = 0\)
Since C(-5) = 0, it is a factor of the numerator, and thus, since the numerator is of the 3rd degree, it can be written as a 3 - 1 = 2nd degree polynomial multiplying x + 5:
\((ax^2 + bx + c)(x + 5) = 4x^3 + 10x^2 + 54x + 520\)
\(ax^3 + (5a + b)x^2 + (5b + c)x + 5c = 4x^3 + 10x^2 + 54x + 520\)
Equaling both sides:
\(a = 4\)
\(b = 10 - 5a = -10\)
\(5c = 520 \rightarrow c = 104\)
Thus:
\(C(x) = (4x^2 - 10x + 104)(x + 5)\)
And:
\(\frac{C(x)}{T(x)} = \frac{(4x^2 - 10x + 104)(x + 5)}{2(x + 5)} = 2x^2 - 5x + 52\)
Thus, the expression is:
\(2x^2 - 5x + 52\)
A similar problem is given at https://brainly.com/question/13586325
a ball is thrown into the air by a baby alien on a planet in the system of alpha centauri with a velocity of 21 ft/s. its height in feet after t seconds is given by y=21t-12t^{2} Find the average velocity for the time period beginning when
Answers
The average velocity for the time period beginning when t=3 and lasting for
1) 0.01 s: -9051.12 ft/sec
2) 0.005 s: -18051.06 ft/sec
3) 0.002 s: -45051.1 ft/sec
4) 0.001 s: -90051 ft/sec
Here, a ball is thrown with initial velocity of 46 ft/s.
The height of the ball in feet after t seconds is given by an equation,
y = 21t - 12t²
Let us assume that P represents the average velocity.
The average velocity is given by formula,
P = [y(t₂) - y(t₁)]/[t₂ - t₁]
i) the average velocity for the time period beginning when t=3 and lasting 0.01 s
Here, t₂ = 3.01 s and t₁ = 3 s
y(t₂) = 21(3.01) - 12(3.01)²
= -45.5112
y(t₁) = 21(3) - 12(3)²
= 45
y(t₂) - y(t₁) = -45.5112 - 45
= -90.5112
So, P = -90.5112 / (0.01)
P = -9051.12 ft/sec
ii) the average velocity for the time period beginning when t=3 and lasting 0.005 s
Here, t₂ = 3.005 s and t₁ = 3 s
y(t₂) - y(t₁) = -45.5112 - 45
= -90.2553
So, P = -90.2553 / (0.005)
P = -18051.06 ft/sec
iii) the average velocity for the time period beginning when t=3 and lasting 0.002 s
Here, t₂ = 3.002 s and t₁ = 3 s
y(t₂) - y(t₁) = -45.1021 - 45
= -90.1021
So, P = -90.1021 / (0.002)
P = -45051.1 ft/sec
iv) the average velocity for the time period beginning when t=3 and lasting 0.001 s
Here, t₂ = 3.001 s and t₁ = 3 s
y(t₂) - y(t₁) = -45.051 - 45
= -90.051
So, P = -90.051 / (0.001)
P = -90051 ft/sec
Learn more about the average velocity here:
https://brainly.com/question/14003954
#SPJ4
The complete question is:
A ball is thrown into the air by a baby alien on a planet in the system of Alpha Centauri with a velocity of 46 ft/s. Its height in feet after t seconds is given by y = 21t - 12t² . A. Find the average velocity for the time period beginning when t=3 and lasting .01 s: .005 s: .002 s: .001 s: NOTE: For the above answers, you may have to enter 6 or 7 significant digits if you are using a calculator. Estimate the instanteneous velocity when t=3.
In a popular online role playing game, players can create detailed designs for their character's "costumes," or appearance. Isabella sets up a website where players can buy and sell these costumes online. Information about the number of people who visited the website and the number of costumes purchased in a single day is listed below.
105 visitors purchased no costume.
41 visitors purchased exactly one costume.
8 visitors purchased more than one costume.
Based on these results, express the probability that the next person will purchase one or more costumes as a decimal to the nearest hundredth.
Answers
The probability that the next person will purchase one or more costumes can be found by dividing the number of visitors who purchased one or more costumes by the total number of visitors.
The total number of visitors is 105 + 41 + 8 = 154.
The number of visitors who purchased one or more costumes is 41 + 8 = 49.
So the probability that the next person will purchase one or more costumes is 49/154, which is approximately 0.32 to the nearest hundredth.
A sociologist wishes to conduct a poll to estimate the percentage of Americans who favor affirmative action program for women and minorities for admission to colleges and universities. What sample size should be obtained if she wishes the estimate to be within a margin of error of 0.04, with 95% confidence, if she uses a 2003 estimate of 0.55 obtained from a Gallup Youth Survey
Answers
Answer:
A sample of 595 should be obtained.
Step-by-step explanation:
In a sample with a number n of people surveyed with a probability of a success of \(\pi\), and a confidence level of \(1-\alpha\), we have the following confidence interval of proportions.
\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In which
z is the zscore that has a pvalue of \(1 - \frac{\alpha}{2}\).
The margin of error is:
\(M = z\sqrt{\frac{\pi(1-\pi)}{n}}\)
Estimate of 0.55
This means that \(\pi = 0.55\)
95% confidence level
So \(\alpha = 0.05\), z is the value of Z that has a pvalue of \(1 - \frac{0.05}{2} = 0.975\), so \(Z = 1.96\).
What sample size should be obtained if she wishes the estimate to be within a margin of error of 0.04?
This is n for which M = 0.04. So
\(M = z\sqrt{\frac{\pi(1-\pi)}{n}}\)
\(0.04 = 1.96\sqrt{\frac{0.55*0.45}{n}}\)
\(0.04\sqrt{n} = 1.96\sqrt{0.55*0.45}\)
\(\sqrt{n} = \frac{1.96\sqrt{0.55*0.45}}{0.04}\)
\((\sqrt{n})^2 = (\frac{1.96\sqrt{0.55*0.45}}{0.04})^2\)
\(n = 594.2\)
Rounding up,
A sample of 595 should be obtained.
between what two consecutive integers must log2(17) lie
Answers
Answer:
4 and 5
Step-by-step explanation:
For answering questions like this, it can be useful to remember a few of the powers of small integers:
2^4 = 16
2^5 = 32
Exponents and logarithmsA logarithm can be considered to be an exponent of the base.
\(\log_b(x) = a \ \Longleftrightarrow\ b^a=x\)
The ordering of powers of 2 relative to the number of interest (17) is ...
16 < 17 < 32
2⁴ < 17 < 2⁵ . . . . . . . . . . . . . . . . . . . expressed as powers of 2
log₂(2⁴) < log₂(17) < log₂(2⁵) . . . . . log₂ of the above inequality
4 < log₂(17) < 5 . . . . . . . . . . . . . . . . showing the values of the logs
Log₂(17) lies between 4 and 5.
__
Additional comment
Using the "change of base" formula, you can use a calculator to find the value of log₂(17). It shows you the value is between 4 and 5.
log₂(17) = log(17)/log(2) . . . . . . using logs to the same base

If it takes one hour for Max to do his homework and it takes Kimberly, his older sister, 1/5 as long to do it. How much longer, in minutes, does it take Max to do his homework than Kimberly?
Answers
Answer:
60-12=48min
Step-by-step explanation:
Kimberly takes 12 min, 1/5 of 60 min.
Um serviço de reparo apresentou valor à vista de R$ 2.500,00 e foi financiado em 6 parcelas mensais e iguais a R$ 363,10, sob o regime de taxa de juros composto, com entrada de R$ 500,00. Determine o valor da taxa de juros compostos imposta no financiamento do serviço de reparo em questão. (Inicie os cálculos com 2,7% a.m. Execute os cálculos com quatro casas decimais.)
Answers
Express your answer in simplest form. 1 3/5 divided by 3/8
Answers
Answer: 1 3/5 divided by 3/8 is equal to 22/3 in simplest form.
Step-by-step explanation:
To express the answer to 1 3/5 divided by 3/8 in simplest form, we first need to convert the mixed number 1 3/5 to an improper fraction. To do this, we can multiply the whole number (1) by the denominator of the fraction (5) and add the numerator (3) to get:
1 * 5 + 3 = 8 + 3 = 11/5
We can then divide this fraction by 3/8 to get the final answer:
$\frac{11/5}{3/8}$
To divide fractions, we can multiply the numerator of the first fraction by the reciprocal of the second fraction:
$\frac{11/5}{3/8} = \frac{11/5}{3/8} \cdot \frac{8/8}{8/8} = \frac{11/5}{3/8} \cdot \frac{8}{3} = \frac{118}{53} = \frac{88}{15}$
Simplifying this fraction gives us:
$\frac{88}{15} = \frac{22}{3}$
Therefore, 1 3/5 divided by 3/8 is equal to 22/3 in simplest form.
How are these two expressions equivalent?

Answers
The expressions In(√2+2) and - In(1-1/√2) are not equivalent.
To determine whether the two expressions are equivalent, we need to evaluate each expression and compare the results.
Expression 1: In(√2+2)
The square root of 2 (√2) is an irrational number approximately equal to 1.414.
Adding 2 to √2 gives us approximately 1.414 + 2 = 3.414.
Taking the natural logarithm (In) of 3.414 will give us the value of the expression.
Expression 2: - In(1-1/√2)
To evaluate - In(1-1/√2), we need to simplify it further.
Let's start by simplifying 1-1/√2:
1 - 1/√2 = (√2/√2) - (1/√2) = (√2 - 1)/√2
Taking the natural logarithm (In) of (√2 - 1)/√2 will give us the value of the expression.
To determine if the two expressions are equivalent, we would need to evaluate the numerical values of In(√2+2) and - In(1-1/√2). However, without the specific values of √2, we cannot compare the results directly.
Therefore, we cannot determine the equivalence of the two expressions without knowing the specific value of √2.
For more such questions on expressions, click on:
https://brainly.com/question/723406
#SPJ8
if x-y = 8 and xy=5 , find x^2 + y^2
Answers
Answer:
x² + y² = 74
Step-by-step explanation:
given
(x - y) = 8 ( square both sides )
(x - y)² = 8² ← expand left side using FOIL
x² - 2xy + y² = 64 ← substitute xy = 5
x² - 2(5) + y² = 64
x² - 10 + y² = 64 ( add 10 to both sides )
x² + y² = 74
Starbucks opened two new locations. Location A costed $800 to open but makes $100 a month. Location B costed $1200 to open but makes $200 a month. Determine how long it will take for the locations to have made the same amount after paying off their costs and how much that amount is. *
Answers
Answer:
I think it is A that will take longer but im not 100 percent sure
Step-by-step explanation:
First write an equation:
Location A- 800+100x
Location B- 1200+200x
Then you need to plug numbers in for x
Determine if the figure is a right triangle by substituting the side lengths into the Pythagorean formula.
Is ABC a right triangle? (0.73 cm) (0.7 cm) (0.24 cm)
Yes or no?

Answers
The figure ABC is not a right triangle
How to determine if the figure is a right triangleFrom the question, we have the following parameters that can be used in our computation:
Side lentghs = (0.73 cm) (0.7 cm) (0.24 cm)
Using the Pythagorean formula, we have
Square of longest sides = Sum of the squares of the other sides
using the above as a guide, we have the following:
0.73² = 0.7² + 0.24²
Evaluate
0.5329 = 0.5476
This equation is false
Hence, ABC is not a right triangle
Read more about right triangle at
https://brainly.com/question/2437195
#SPJ1
a student skipped a step when he tried to convert 1020 seconds into hours and got the following incorrect result
1020seconds (1hours/60mins)=17hours
what conversion ratio did he skip in this multiple-step conversion
Answers
Answer:That student has forgot to convert it into minutes and then convert it to hours
Step-by-step explanation:
1020/7=17 minutes and
17/60=0.283hours