To begin a bacteria study, a petri dish had 2700 bacteria cells. Each hour since, the number of cells has increased by 5. 2%.
Let t be the number of hours since the start of the study. Let y be the number of bacteria cells.
Write an exponential function showing the relationship between y and t.
Answers
The exponential function y = \(2700(1.02)^t\) models the growth of bacteria cells in a petri dish over time, with an initial population of 2700 cells and a growth rate of 2% per hour.
Exponential functions are often used to model situations where the growth or decay of a quantity depends on a constant proportionality factor.
In this case, the proportionality factor is the growth rate, which is represented by the constant 0.02 in the function. The factor (1 + r) represents the growth factor, which is the multiplier for the initial population to calculate the population after t hours. The larger the growth rate, the faster the population will grow, and the steeper the graph of the exponential function will be.
The equation y = \(2700(1.02)^t\) can be used to make predictions about the growth of the bacteria population over time. For example, after one hour, the number of bacteria cells would be y = \(2700(1.02)^1\) = 2754 cells. After two hours, the number of cells would be y = \(2700(1.02)^2\) = 2812 cells, and so on.
It's worth noting that exponential growth cannot continue indefinitely, as there are always limiting factors that will eventually constrain the growth of a population. In the case of bacteria, the petri dish may eventually become overcrowded or run out of nutrients, which will slow or stop the growth of the bacteria population. Therefore, the exponential function y = \(2700(1.02)^t\) is a model that is only valid for a certain range of values of t, beyond which other factors may come into play.
To learn more about exponential function refer here:
https://brainly.com/question/14355665
#SPJ11
Related Questions
What is the circumference of the field? *
a circular field has a area of 14400 sq ft
Answers
Answer:
425.39
Step-by-step explanation:
4 glue sticks cost $7.76. Write a proportion
Answers
Divide 7.76 by 4 to get the cost of each glue stick
The following are the annual operations. The interest rate for the first fourteen years is 1% per month and thereafter will be 1.5% per month: $100,000 will be contributed at the end of each year for 8 years. end of each year for 8 years (the first is at the end of year 1); equal annual withdrawals will be made from the end of year 10 to the end of year 14 of $60,000; finally, equal contributions of $50,000 will be made from the end of year 15 to the end of year 20.
8. Calculate the effective annual interest rates: Answer 12.6825% and 19.56182%.
9. Calculate the balance in present value: Answer $444,117.28
10. Calculate the balance in future value: Answer $6,903,087.93
Answers
Effective annual interest rates: 12.6825% for the first 14 years, 19.56182% thereafter.
Balance in present value: $444,117.28.
Balance in future value: $6,903,087.93.
The effective annual interest rates for the given operations are 12.6825% for the first 14 years and 19.56182% thereafter. These rates take into account compounding on a monthly basis and reflect the actual annual return on the investments.
To calculate the effective annual interest rate for the first 14 years, we can use the formula: (1+monthly interest rate)12−1(1+monthly interest rate)12−1. Plugging in the monthly interest rate of 1%, we find that the effective annual interest rate is 12.6825%.
For the period after 14 years, the effective annual interest rate can be calculated using the same formula, but with the monthly interest rate of 1.5%. Substituting this value, we obtain an effective annual interest rate of 19.56182%.
The balance in present value can be calculated as the sum of the present values of the contributions and withdrawals. The present value of a cash flow can be calculated using the formula: FV(1+r)n(1+r)nFV, where FV is the future value, r is the interest rate, and n is the number of periods.
To calculate the balance in present value, we need to determine the present value of the contributions, withdrawals, and future contributions. Applying the formula for each cash flow and summing them up, we find that the balance in present value is $444,117.28.
The balance in future value can be calculated as the sum of the future values of the contributions and withdrawals. The future value of a cash flow can be calculated using the formula: PV×(1+r)nPV×(1+r)n, where PV is the present value, r is the interest rate, and n is the number of periods.
To calculate the balance in future value, we need to determine the future value of the contributions, withdrawals, and future contributions. Applying the formula for each cash flow and summing them up, we find that the balance in future value is $6,903,087.93.
learn more about "interest ":- https://brainly.com/question/25720319
#SPJ11
How many grams are in 4.3 moles of ammonium chloride
Answers
Answer:
230 g
Step-by-step explanation:
4.3 x molar mass of NH4Cl
Molar Mass of NH4Cl = 14.0067 + 4x1.0079 + 35.453 = 53.491
4.3 x 53.491 = 230 g
If they can travel 30 miles on one gallon of gas, and their family car has an 18-gallon tank, how many miles can they travel on one tank of gas?
Answers
The figure shows the dimensions for a package to be shipped.
6 in.
4 in.
-12 in.
10 in.
sq. in.
15 in.
What is the minimum amount of wrapping paper, in square inches, needed to cover the package?

Answers
The minimum amount of wrapping paper, needed to cover the package surface area is 174 square inches.
Total surface area = Area of 2 similar trapeziums + Area of rectangles of 4 different rectangles
area of a triangle = 1/2 ×Base×Height and area of a rectangle is Length×Breadth.
= 2×1/2(7+3)×3+8×5+8×3+8×3+8×7
= 174 square inches
To learn more about the surface area, here:
brainly.com/question/26403859.
#SPJ1
Which of the following constructions must you know how to do in order to construct an inscribed circle for a given triangle?
angle bisector
perpendicular bisector
duplicating a line segment
bisecting a segment
Answers
For the construction of an inscribed circle the required construction that must be known is the angle bisector. The correct option is (A).
What is an angle bisector?The angle bisector is a line that divides an angle into two equal parts. For a circle inscribed in a triangle the line joining the center to the vertex is the angular bisector of the interior angle.
The diagram for the given case can be drawn as follows,
For the circle inscribed in the circle, all the sides are tangents.
By the property of tangents to a circle ∠ODB and ∠OFB are right angles.
Now, in ΔODB and ΔOFB the relation is obtained as,
∠ODB = ∠OFB (right angles)
OB = OB (Common sides)
And, OD = OF (radius of the circle)
⇒ ΔODB ≅ ΔOFB (by RHS criteria)
This implies that ∠ODB ≅ ∠OFB.
Thus, the line joining the centre and the vertex of triangle bisects its angles.
Hence, for the given case the required construction to be known is the angle bisector of triangle.
To know more about angle bisector click on,
https://brainly.com/question/12896755
#SPJ1
Solve this question with full working and explanation and I will mark you as brainliest.

Answers
Answer:
The hand moved \(\bf \frac{3}{4}\) of a complete turn.
Step-by-step explanation:
The hand moved from 3 to 12, that is, it moved:
12 - 3 = 9 hours
In a clock, 12 hours represent a complete turn.
∴ Using the unitary method:
12 hours ⇒ 1 turn
1 hour ⇒ \(\frac{1}{12}\) turns
9 hours ⇒ \(\frac{1}{12}\) × 9 = \(\frac{9}{12}\)
= \(\bf \frac{3}{4}\) turns (simplified)
∴ The hand moved \(\bf \frac{3}{4}\) of a complete turn.
The answer is \(\boxed{\frac{3}{4}}\).
To find the fraction of a complete turn it moved in this case, take the ratio between hours covered between 3 and 12, and the hours covered in a complete turn.
Hours covered between 3 and 12 : 12 - 3 = 9Hours covered in a complete turn = 12Fraction of a complete turn it moved : 9/12 = 3/4You need a simple interest bridge loan to cover the costs of buying a new home while waiting to close on your old one. You need to finance $73,000 and bank will charge 6%. How much interest will you pay if you needed the loan for 9 months?Interest =$(nearest $1)
Answers
The problem says you need a simple interest bridge loan.
You need to finance $73,000.
The interest rate is 6% (0.06)
You need the loan for 9 months.
The formula for simple interest rate is the following:
\(SI=P\cdot r\cdot t\)Where SI is the simple interest. P is the principal or money borrowed. r is the interest rate in decimal form. t is the time in years.
As you need the loan for 9 months, we need to convert it to years, as follows:
\(9\text{months}\cdot\frac{1\text{year}}{12months}=0.75years\)Now, replace the known values and solve for SI:
\(\begin{gathered} SI=73,000\cdot0.06\cdot0.75 \\ SI=3,285 \end{gathered}\)You will pay $3,285 interest for the loan.
There are 86{,}40086,40086, comma, 400 frames of animation in 111 hour of anime. How many frames are there per second? There are 3600 seconds in one hour
Answers
Answer
24 frames per second
Step-by-step explanation:
Total frames=86,400
Total time=1 hour
Find frame per second
1 hour= 60 minutes*60 seconds
1 hour=3600 seconds
Frame per second=Total frames/Total number of seconds
=86,400/3600
=24 frames per second
The number of monthly breakdowns of a conveyor belt at a local factory is a random variable having the Poisson distribution with λ = 2.8. Find the probability that the conveyor belt will function for a month without a breakdown. (Note: please give the answer as a real number accurate to 3 decimal places after the decimal point.)
Answers
The probability that the conveyor belt will function for a month without a breakdown is approximately 0.061 (accurate to 3 decimal places after the decimal point).
To find the probability that the conveyor belt will function for a month without a breakdown, given that the number of monthly breakdowns follows a Poisson distribution with λ = 2.8, we will use the Poisson probability formula:
P(X = k) = (e^(-λ) * (λ^k)) / k!
In this case, k = 0 (no breakdowns) and λ = 2.8. Plug these values into the formula:
P(X = 0) = (e^(-2.8) * (2.8^0)) / 0!
P(X = 0) = (e^(-2.8) * 1) / 1
Now, use a calculator or software to compute e^(-2.8) and multiply it by 1:
P(X = 0) ≈ 0.06078
So, the required probability is approximately 0.061 (accurate to 3 decimal places after the decimal point).
To learn more about Poisson distribution visit : https://brainly.com/question/9123296
#SPJ11
The large rectangle below represents one whole. A large rectangle with 25 equal sections, 11 of which are shaded What percent is represented by the shaded area?
Answers
fourty four percent hope this helps !
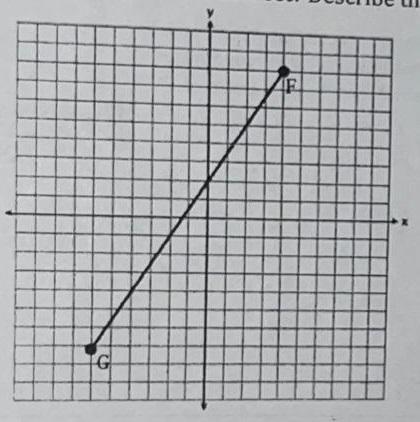
Loule and Nicky were asked to find point P that divides the directed line segment FG so that the ratio of FP to PG is 4 to 1. Loule says the coordinate of point P is (-4,-4), while Nicky says the coordinate of point P is (2, 5). Who is correct? Describe the mistake that was made by the student who was incorrect
Answers
Using ratio and proportion, Louie is correct.
Ratio is defined as the relationship between two quantities. On the other hand, proportion is defined as the equality between two or more ratios.
From the given graph (see attached photo), the coordinates of Point F and Point G is (4, 8) and (-6, -7).
If the ratio of FP to PG is 4 to 1, then the ratio of the horizontal distance and vertical distance between the two endpoints is also 4 to 1.
FP : PG = 4 : 1
FP/PG = 4/1 = 4
x-coordinate of P
(4 - x)/(x - -6) = 4
(4 - x) = 4(x + 6)
4 - x = 4x + 24
-5x = 20
x = -4
y-coordinate of P
(8 - y)/(y - -7) = 4
(8 - y) = 4(y + 7)
8 - y = 4y + 28
-5y = 20
y = -4
Hence, the coordinates of Point P is (-4, -4).
Therefore, Louie is correct, while Nicky is mistaken probably while setting up the proportion and solving for the coordinates.
Learn more about ratio and proportion here: https://brainly.com/question/23431895
#SPJ4
green eggs and ham find the area of the domain enclosed by the curve with parametric equations x = tsin t, y = cost, t ∈ [0, 2π].
Answers
The area of the domain enclosed by the curve with parametric equations x = tsin t, y = cost, t ∈ [0, 2π] is 2π + 2.
The parametric equations given are:
x = t sin t
y = cos t
To find the area of the domain enclosed by the curve, we can use the formula for the area of a region bounded by a curve given in parametric form:
A = ∫[a,b] y dx
where a and b are the limits of the parameter t that describe the domain of the curve.
In this case, we have:
a = 0
b = 2π
So, we need to compute:
A = ∫[0,2π] cos(t) (t sin(t)) dt
Using integration by parts with u = t and dv = sin(t) dt, we get:
A = [t cos(t)]|[0,2π] - ∫[0,2π] cos(t) dt + ∫[0,2π] sin(t) dt
The first integral evaluates to:
[t cos(t)]|[0,2π] = 2π
The second integral evaluates to:
∫[0,2π] cos(t) dt = [sin(t)]|[0,2π] = 0
The third integral evaluates to:
∫[0,2π] sin(t) dt = [-cos(t)]|[0,2π] = 2
Therefore, the area of the domain enclosed by the curve is:
A = 2π - 0 + 2 = 2π + 2
To learn more about parametric equations go to:
https://brainly.com/question/29275326
#SPJ11
Which ordered pairs make both inequalities true? Check all that apply

Answers
Answer:.
Step-by-step explanation:
Match the following values as a A) discrete random variable, B) continuous random variable, or C) not a random variable: Exact weight of quarters now in circulation in the United States ________ Shoe sizes of humans ________ Political party affiliations of adults in the United States ________
Answers
Answer:
Exact weight of quarters now in circulation in the United States (continuous random variable )
Shoe sizes of humans (discrete random variable)
Political party affiliations of adults in the United States ( random variable)
Step-by-step explanation:
continuous random variable: this is a random experiment where the data usually assume an infinite mode. meaning it is continuous.
discrete random variable: this is the assigning of values based on the outcome of a radom experiment.
random variable: a random variable is a set of possible outcomes from a random experiment
marcus borrows $3,000 from his local credit union, to be repaid with 3.5% simple interest over 4 years. What are the principal, interest rate, and time in this situation?
Answers
Interest rate=3.5
Time=4 years
=42k
Doug, who runs track for his high school, was challenged to a race by his younger brother, matt. Matt started running first, and doug didn’t start running until matt had finished a quarter-mile lap on the school track. Doug passed matt as they both finished their sixth lap. If both boys ran at a constant speed, with doug running 2 miles an hour faster than matt, what was matt’s speed?.
Answers
Doug passed the matt as they both finished their sixth lap. If both boys ran at a constant speed, with doug running 2 miles an hour faster than matt, the speed of the matt is 10 miles per hour.
Doug ran 2 miles an hour faster than Matt, so let Matt’s speed equal x miles per hour. Then the Doug’s speed equals to x + 2 miles per hr. Each of the lap is one-quarter of a mile, so the Doug runs 1.5 miles the time it takes Matt to run 1.25 miles. Place this information in a chart:
Rate Time
Doug x+2 1.5/x+2
Matt x 1.25/x
Doug and Matt took the same amount of time from the time as Doug started, lets make an equation by setting the two times in the equation equal to each other, and then solve for x:
1.5/x+2 = 1.25/x
1.5x = 1.25(x+2)
1.5x = 1.25x+2.5
0.25x = 2.5
x = 10
The Matt ran at 10 miles per hour.
learn more about speed and miles here :
https://brainly.com/question/27274794
#SPJ4
show how the parameters in the two equations are related
Answers
The method for determining the similar relationship between the parameters of two equations has been explained below.
The relationship between parameters in two equations depends on the specific equations and parameters involved. In general, parameters are constants or variables that are used to define or modify the behavior of a mathematical or physical system.
If two equations have the same parameters, then changes in those parameters will affect the behavior of both equations in the same way and if they have different parameters, then changes in those parameters may affect the behavior of the equations differently. In general, to determine the relationship between parameters in two equations, you would need to analyze the equations and their specific parameters to understand how they are related.
Learn more about the parameter of equations on
https://brainly.com/question/30117042?referrer=searchResults
#SPJ4
If you enter into an annual contract but decide to leave after 5 months, how much do your parents lose by not doing the month-to-month contract?
Answers
By choosing the annual contract and breaking it after 5 months, your parents would lose $574.00.
How much do your parents lose by not doing the contract?If you enter into an annual contract at $467.00/month and break it after 5 months, you would have paid:
= $467.00 x 5
= $2,335.00
Since breaking the annual contract incurs a penalty of 2 months' rent, your parents would need to pay an additional of:
= $467.00 x 2
= $934.00
If parents opted for the month-to-month contract at $539.00/month, the total cost for 5 months would be:
= $539.00 * 5 month
= $2,695.00.
So, by choosing the annual contract and breaking it after 5 months, your parents would lose:
= $3,269.00 - $2,695.00
= $574.00.
Full question "Your parents are considering renting you an apartment instead of paying room and board at your college. The month-to-month contract is $539.00/month and the annual contract is $467.00/month. If you break the annual contract, there is a 2-month penalty. If you enter into an annual contract but decide to leave after 5 months, how much do your parents lose by not doing the month-to-month contract."
Read more about contract
brainly.com/question/5746834
#SPJ1
The prices of consumer goods do not always exactly follow the CPI. The following chart shows several consumer items, along with their respective prices in 1983 and today.ItemPrice in 1983 ($)Current Price ($)Pair of boots67.45126.85Hair dryer15.2529.95Box of tissues1.152.25Toaster22.8544.25Using the prices shown on this chart, which of the following is a reasonable estimate of the current CPI?a. 208b. 195c. 180d. 173
Answers
None of the given options (i.e. a, b, c, or d) is correct.
Given the prices of consumer items, we can find the estimate of the current CPI.
The percentage change in the price of the consumer item over time can be given as:
Percentage change = (Current Price − Price in 1983)/Price in 1983 × 100%
Now, using the percentage change we can find the average percentage change (increase or decrease) in prices. We calculate the average percentage change by finding the sum of the percentage change in prices of all items and then dividing it by the number of items.
Thus, we have:
Average percentage change = [(126.85−67.45)/67.45 + (29.95−15.25)/15.25 + (2.25−1.15)/1.15 + (44.25−22.85)/22.85]/4Average percentage change = 4.4188%
Now, the current CPI can be found using the following formula:
Current CPI = CPI in 1983 × [1 + (Average percentage change)/100]Current CPI = 100 × [1 + 4.4188/100] ≈ 104.42 ≈ 104
Therefore, the reasonable estimate of the current CPI is 104.
None of the given options (i.e. a, b, c, or d) is correct.
To learn more about “ CPI” refer to the https://brainly.com/question/8416975
#SPJ11
a. Find the value of a. b. Find the value of the marked angles.A. 21; 137B. 20; 131C. 17; 113D. 18; 119

Answers
Both are vertical angles (opposite)
So, they are congruent ( equal)
6a +11 = 2a+83
Solve for a:
6a -2a = 83-11
4a= 72
a= 72/4
a= 18
Value of the angles:
6a+11 = 6(18)+11 = 108+11 = 119°
2a+83 = 2(18)+83 =
A rope goes from one building to another. The distance between the buildings is 10m, and the rope is tied at each building at a point 8m and 4m from the ground. Find the length of the rope.
Answers
Answer:
Step-by-step explanation:
Think of it as a triangle.
They give you the length of the bottom side and the location of the tops of the buildings.
You need to find the hypotenuse ( the longest side or the length of the rope)
Use the pythagorean theorem
\(a^{2} + b^{2} = c^{2}\)
10 ^2 + 4^2= c^2
100 + 16 = c^2
116 = c^2
c is about 10.77

The length of the rope is 10.77 m
What is a Triangle?
A triangle is a plane figure or polygon with three sides and three angles.
A Triangle has three vertices and the sum of the interior angles add up to 180°
Let the Triangle be ΔABC , such that
∠A + ∠B + ∠C = 180°
For a right angle triangle
From the Pythagoras Theorem , The hypotenuse² = base² + height²
Given data ,
Let the length of the rope be = H
Let the distance between the two buildings be L = 10 m
Let the height of the first building be A = 8 m
Let the height of the second building B = 4 m
Now ,
The expressions form a right angled triangle with the base of the triangle has a length of 10 m and the height of the triangle is 4m
Height of the triangle = A / 2 = 4m
So , the hypotenuse of the triangle will be the length of the rope
From the Pythagoras Theorem , The hypotenuse² = base² + height²
So , H² = ( A / 2 )² + L²
Substituting the values , we get
H² = 4² + 10²
H² = 16 + 100
H² = 116
Taking square roots on both sides , we get
H = √116
H ≈ 10.77 m
Therefore , the value of H is 10.77 m
Hence , The length of the rope is 10.77 m
To learn more about triangles click :
https://brainly.com/question/16739377
#SPJ2
Which of the following shows the extraneous solution to the logarithmic equation? log Subscript 4 Baseline (x) log Subscript 4 Baseline (x minus 3) = log Subscript 4 Baseline (negative 7 x 21).
Answers
By solving the given equation and then substituting solution in original equation we found out that x=3 and x=-7 are extraneous solution.
What is Extraneous solutions?
The extraneous solutions are the solutions that does not work in the original equation.
Original equation
\($\log _{4}(x)+\log _{4}(x-3)=\log _{4}(-7x+21)$\)
Now we will simplify this
\(\log _{4}(x(x-3))=\log _{4}(-7 x+21)$\\\\x(x-3)=-7 x+21\\\\&x^{2}-3 x=-7 x+21 \\\\\\&x^{2}-3 x+7 x-21 =0\\\\&x^{2}+4 x-21=0\\\\\\&x^{2}-3 x+7x-21=0\\\\\\(x-3)(x+7)=0\\x=3,-7\)
Now, we will determine the extraneous solution, by substituting x=3 and x=-7 in the originally given equation.
Substituting x=3,
\(\log _{4}(3)+\log _{4}(3-3)=\log _{4}(-21+21) \\\\\log _{4}(3)+\log _{4}(0)=\log _{4}(0)\)
As we know log(0) is undefined , Hence x=3 is extraneous solution
Now Substituting x=-7
\(\log _{4}(-7)+\log _{4}(-7-3)=\log _{4}(-7(-7)+21)\\\\\log _{4}(-7)+\log _{4}(-10)=\log _{4}(-28)\)
As we know log is not defined for negative numbers hence x=-7 is extraneous solution
By solving the given equation and then substituting solution in original equation we found out that x=3 and x=-7 are extraneous solution
To know more about logarithm function visit : https://brainly.com/question/13473114
Sarah says “if you subtract 11 from my number and multiply the difference by -3,the result is -36. What is Sara’s number
Answers
Answer:
n = 23
Step-by-step explanation:
Let Sara's number be n. Then -3(n - 11) = -36
Solve for n - 11 by dividing both sides by -3: n - 11 = 12.
Adding 11 to both sides yields n = 23
Answer:
i believe that the correct answer is -1

Banks and other financial institutions offer incentives for people to keep their money in a savings account.
True or False?
Answers
it's true because it gives interset or compensation amount to the individuals or organizations which motivates people to save their money in a saving account
Your weekly net income is $380. Your total budgeted monthly expenses $1. 550,00. Do you have a surplus or deficit balance at the end of the month?
Answers
We will have a Deficit balance of $30 at the end of the month.
"Unilateral transfer" is the term used to describe the balance of payments deficit's most obvious cause. For instance, Americans who contribute money to another country in the form of foreign aid do not receive anything in return (economically speaking). Few economists would argue that foreign aid-related balance of payment deficits are a "bad thing."
Weekly net income = $380
Monthly net income = $380 * 4 weeks = $1520.
Monthly expenses = $1550
Balance = Monthly income - monthly expenses = $-30.
The negative sign shows a deficit of $30 monthly
Therefore, We will have a Deficit balance of $30 at the end of the month.
To learn more about Deficit, visit the link below:
brainly.com/question/2290367
#SPJ4
find perimeter of a semicircle that has radius of 6cm (give answer in 2 d.p)
Answers
Answer:
30.84 cm
Step-by-step explanation:
Formula for perimeter of semi-circle = πr + 2r
Radius (r) = 6 cm
π = 3.14
Perimeter
= πr + 2r
= 3.14(6) + 2(6)
= 3.14(6) + 12
= 18.84 + 12
= 30.84 cm
_________
Hope it helps ⚜
Answer:
30.85 cm to 2 d.p.
Step-by-step explanation:
The perimeter is made up of the diameter ( = 2*radius) and half a full circle
= 6*2 + 1/2 * π* 6
= 12 + 3π
= 30.849
What is the volume of this triangular prism?

Answers
Answer:
576 cm squared
Step-by-step explanation:
need help quick, please and thank tou

Answers
Answer: C
Step-by-step explanation: