Tickets to the baseball game are on sale for $1.50 off the regular price. Dea buys 6 tickets. If her total cost is $51, what is the regular price of each ticket? Write and solve an equation of the form p(x±q)=r. Then write a sentence to explain your answer.
Answers
Answer:
Below
Step-by-step explanation:
6 (x-1.50) = 51 6 = number of tix x - 1.50 = sale price x = reg price
6x - 9 = 51
6x = 60
x = 10 dollar regular price
Related Questions
A certain college graduate borrows $6600 to buy a car. The lender charges interest at an annual rate of 10%. Assuming that interest is compounded continuously and that the borrower makes payments continuously at a constant annual rate k dollars per year, determine the payment rate k that is required to pay off the loan in 5 years. (Round your answer to two decimal places.) k = $ per yr
Answers
The borrower would need to make payments of approximately $943.57 per year to pay off the loan in 5 years.
To determine the payment rate required to pay off the loan in 5 years, we can use the continuous compound interest formula:
A = P * \(e^{(rt)\),
where A is the final amount, P is the initial principal, e is the base of the natural logarithm (approximately 2.71828), r is the annual interest rate, and t is the time in years.
In this case, the initial principal is $6600, the annual interest rate is 10%, and the time is 5 years. We want to find the payment rate, so let's set A equal to zero, indicating that the loan is fully paid off:
0 = 6600 * \(e^{(0.10 * 5)\)- k * 5,
Simplifying the equation, we have:
\(e^{(0.5)\) = k / 6600.
Now, we can solve for k by multiplying both sides of the equation by 6600:
k = 6600 * \(e^{(0.5)\),
Using a calculator or software, we find that k is approximately $943.57 per year.
To learn more about payment rate click on,
https://brainly.com/question/14806350
#SPJ4
Please help me !! would appreciate

Answers
The answers that describe the quadrilateral DEFG area rectangle and parallelogram.
The correct answer choice is option A and B.
What is a quadrilateral?A quadrilateral is a parallelogram, which has opposite sides that are congruent and parallel.
Quadrilateral DEFG
if line DE || FG,
line EF // GD,
DF = EG and
diagonals DF and EG are perpendicular,
then, the quadrilateral is a parallelogram
Hence, the quadrilateral DEFG is a rectangle and parallelogram.
Read more on quadrilaterals:
https://brainly.com/question/23935806
#SPJ1
Help please 10 pts!!!

Answers
Answer:
2 cups
Step-by-step explanation:
to make one cup of orange
1/3 (multiply by 3) = 1 cup
then also multiply 2/3 by 3 =2
so you need 2 cups of pineapple
What is the breakdown of this math problem? 8 2/5 - 6 7/10 =
Answers
let's first off, convert the mixed fractions to improper fractions.
\(\stackrel{mixed}{8\frac{2}{5}}\implies \cfrac{8\cdot 5+2}{5}\implies \stackrel{improper}{\cfrac{42}{5}}~\hfill \stackrel{mixed}{6\frac{7}{10}} \implies \cfrac{6\cdot 10+7}{10} \implies \stackrel{improper}{\cfrac{67}{10}} \\\\[-0.35em] ~\dotfill\\\\ \cfrac{42}{5}-\cfrac{67}{10}\implies \cfrac{(2)42~~ - ~~(1)67}{\underset{\textit{using this LCD}}{10}}\implies \cfrac{84-67}{10}\implies \cfrac{17}{10}\implies 1\frac{7}{10}\)
What is the volume of a sphere with a diameter of 2.2 ft, rounded to the nearest tenth
of a cubic foot?
Answers
Answer:
V≈5.58ft³ d=2.2 ft
Step-by-step explanation:
V=4 3πr3
d=2r
Solving for V
V=1 6π d3 =1 6·π·2.23≈5.57528ft³
Hope this helps! :D
Answer:
5.6 ft
Step-by-step explanation:
\text{Volume of a Sphere:}
Volume of a Sphere:
V=\frac{4}{3}\pi r^3
V=
3
4
πr
3
\text{radius} = \frac{\text{diameter}}{2} = \frac{2.2}{2}=1.1
radius=
2
diameter
=
2
2.2
=1.1
feet
\text{Plug in:}
Plug in:
\frac{4}{3}\pi (1.1)^3
3
4
π(1.1)
3
5.57527976257
A researcher obtains z = 1.80 for a one-sample z test. What is the decision for this test at a .05 level of significance?
Group of answer choices
a. to reject the null hypothesis
b. to retain the null hypothesis
c. It depends on whether the test is one-tailed or two-tailed.
d. There is not enough information to make a decision.
Answers
The decision for this test at a .05 level of significance is not enough information to make a decision the correct answer is (d).
To make a decision for a hypothesis test, we compare the obtained test statistic (in this case, z = 1.80) with the critical value(s) based on the chosen level of significance (in this case, α = 0.05).
For a one-sample z test, if the obtained test statistic falls in the rejection region (i.e., beyond the critical value(s)), we reject the null hypothesis. Otherwise, if the obtained test statistic does not fall in the rejection region, we fail to reject the null hypothesis.
Without knowing the critical value(s) corresponding to a significance level of 0.05 and the directionality of the test (one-tailed or two-tailed), we cannot determine the decision for this test. Therefore, the correct answer is (d) There is not enough information to make a decision.
Learn more about z test at https://brainly.com/question/32334731
#SPJ11
A cell phone provider will allow you to buy a phone over time. They require a $50 initial payment and then charge $25 per month. If this situation were represented by a function, what would be the slope?
50
25
75
0
Answers
Answer:
slope is 25 because the equation is y=25x+50
Step-by-step explanation:
heres the official answer
( Let C be the curve which is the union of two line segments, the first going from (0,0) to (-2,-1) and the second going from (-2,-1) to (-4, 0). Compute the line integral ∫ C –2dy+ 1dx .
Answers
The line integral ∫C -2dy + 1dx is equal to 0 for C1 and -4 for C2.
To compute the line integral ∫C -2dy + 1dx, we need to parameterize the curve C and then evaluate the integral along that parameterization.
The curve C consists of two line segments. Let's denote the first line segment as C1 and the second line segment as C2.
C1 goes from (0, 0) to (-2, -1), and C2 goes from (-2, -1) to (-4, 0).
Let's parameterize C1 using t ranging from 0 to 1:
x(t) = (1 - t) * 0 + t * (-2) = -2t
y(t) = (1 - t) * 0 + t * (-1) = -t
Now, let's parameterize C2 using s ranging from 0 to 1:
x(s) = -2 + s * (-4 - (-2)) = -2 - 2s
y(s) = -1 + s * (0 - (-1)) = -1 + s
We can now compute the line integral ∫C -2dy + 1dx by splitting it into two integrals corresponding to C1 and C2:
∫C -2dy + 1dx = ∫C1 -2dy + 1dx + ∫C2 -2dy + 1dx
For C1, we have:
∫C1 -2dy + 1dx = ∫[0,1] -2(-dt) + 1(-2dt) = ∫[0,1] 2dt - 2dt = ∫[0,1] (2 - 2) dt = 0
For C2, we have:
∫C2 -2dy + 1dx = ∫[0,1] -2(ds) + 1(-2ds) = ∫[0,1] (-2 - 2ds) = ∫[0,1] (-2 - 4s)ds = -2s - 2s^2 evaluated from s = 0 to s = 1 = -2 - 2 = -4.
For more such questions on integral visit:
https://brainly.com/question/30094386
#SPJ8
(WILL GIVE BRAINLIEST) Solve for x.
-2(-9x+5)-4x=2(x-5)-4
Simplify your answer as much as possible
Answers
Answer:
−2(−9x+5)−4x=2(x−5)−4
Step 1: Simplify both sides of the equation.
−2(−9x+5)−4x=2(x−5)−4
(−2)(−9x)+(−2)(5)+−4x=(2)(x)+(2)(−5)+−4(Distribute)
18x+−10+−4x=2x+−10+−4
(18x+−4x)+(−10)=(2x)+(−10+−4)(Combine Like Terms)
14x+−10=2x+−14
14x−10=2x−14
Step 2: Subtract 2x from both sides.
14x−10−2x=2x−14−2x
12x−10=−14
Step 3: Add 10 to both sides.
12x−10+10=−14+10
12x=−4
Step 4: Divide both sides by 12.
12x
12
=
−4
12
x= -1/3
Step-by-step explanation:
Good luck! Hope this helps! <3
Answer :
\(x = - \frac{1}{3} \)
or you can just write x = -0.3
hope this helps!
a) Verify that the function y=x^2 + c/x^2 is a solution of the differential equation xy' + 2y = 4x^2, (x > 0). b) Find the value of c for which the solution satisfies the initial condition y(8) = 6. C = ___
Answers
a) the function y=x^2 + c/x^2 is a solution of the differential equation xy' + 2y = 4x^2, (x > 0).
b) The value of c for which the solution satisfies the initial condition y(8) = 6 is c = -3712.
a) To verify that the function y = x^2 + c/x^2 is a solution of the differential equation xy' + 2y = 4x^2, we first need to find the derivative y' using algebra:
y = x^2 + c/x^2
y' = 2x - 2c/x^3
Now, plugging y and y' into the given differential equation:
x(2x - 2c/x^3) + 2(x^2 + c/x^2) = 4x^2
Next, simplify the equation:
2x^2 - 2cx^(-2) + 2x^2 + 2c/x^2 = 4x^2
Combine the like terms:
4x^2 = 4x^2
The equation holds true, so the function y = x^2 + c/x^2 is a solution of the differential equation xy' + 2y = 4x^2.
b) To find the value of c for which the solution satisfies the initial condition y(8) = 6, plug in x = 8 and y = 6 into the function y = x^2 + c/x^2:
6 = (8^2) + c/(8^2)
Solve for c:
6 - 64 = c/64
-58 = c/64
c = -58 * 64
So, the value of c is -3712.
Learn more about the Algebra of derivatives: https://brainly.com/question/28376218
#SPJ11
A water tank is 1•2m square and 1•35m deep. It is half full of water. How many times can a 9-litre bucket be filled from the tank
Answers
Answer:
180
Step-by-step explanation:
Volume = base * height(depth)
V=1.2*1.35=1.62 m³
1 m³=1000 liter
1.62*1000=1620 liter
1620/9=180 ( 9 liter bucket)
When constructing an inscribed hexagon by hand, which step comes after constructing a circle?.
Answers
After constructing a circle, the next step in constructing an inscribed hexagon by hand is to draw two diameters of the circle that are perpendicular to each other.
Drawing two diameters of the circle that are perpendicular to each other is the next step in constructing an inscribed hexagon because it helps to determine the positions of the vertices of the hexagon. The diameters divide the circle into four equal quadrants, with the center of the circle as the point of intersection. By connecting the points where the diameters intersect the circle, we can identify the six vertices of the hexagon. These vertices will lie on the circumference of the circle and will form the six sides of the inscribed hexagon.
To know more about hexagon,
https://brainly.com/question/29153003
#SPJ11
Which of these is a zero of the polynomials p(y) = 3y^3 - 16 y - 8? * - 8 0 2 - 2
Answers
The zero of polynomials is -2. The polynomials is p(y) = \(3y^{3} - 16 y - 8\).
According to the question,
The polynomials is p(y) = \(3y^{3} - 16 y - 8\). In order to find the zero of polynomials only if we substitute the value and polynomials become zero.
p(-2) = \(3(-2)^{3} - 16 (-2) - 8\)
= 3(8) + 32 -8
= 0
Hence, the zero of polynomials is -2. The polynomials is p(y) = \(3y^{3} - 16 y - 8\).
Learn more about polynomials here
https://brainly.com/question/1720316
#SPJ4
Given the following information write the equation of the line
b=8; m=5/2
Answers
Answer:
Step-by-step explanation:

Hello! I really need some help with this (:

Answers
Answer:
y = 3x + 3
Step-by-step explanation:
As x increases, y increases by 3. Therefore, the slope of the function is 3.
Setting x = 0 will give an output of 3. Therefore, the y-intercept is (0, 3).
Overall, the function rule for the given data set is y = 3x + 3.
an 8 sided regular polygon (regular octagon) is inscribed in a circle whose radius is 16 feet. find the area of the polygon.
Answers
The area of the regular octagon inscribed in a circle with a radius of 16 feet can be found using the formula A = (2 + 2sqrt(2))r^2, where r is the radius of the circle. Plugging in the value for r, we get:
A = (2 + 2sqrt(2))(16)^2
A = (2 + 2sqrt(2))(256)
A = 660.254 ft^2
Therefore, the area of the regular octagon is approximately 660.254 square feet.
To derive the formula for the area of a regular octagon inscribed in a circle, we can divide the octagon into eight congruent isosceles triangles, each with a base of length r and two congruent angles of 22.5 degrees. The height of each triangle can be found using the sine function, which gives us h = r * sin(22.5). Since there are eight of these triangles, the area of the octagon can be found by multiplying the area of one of the triangles by 8, which gives us:
A = 8 * (1/2)bh
A = 8 * (1/2)(r)(r*sin(22.5))
A = 4r^2sin(22.5)
We can simplify this expression using the double angle formula for sine, which gives us:
A = 4r^2sin(45)/2
A = (2 + 2sqrt(2))r^2
Therefore, the formula for the area of a regular octagon inscribed in a circle is A = (2 + 2sqrt(2))r^2.
To learn more about regular octagon : brainly.com/question/1386507
#SPJ11
Consider a multiple channel line with 5 cashiers. The customer arrival rate, $\lambda$, is $85.5 /$ hour, and the service rate, $\mu$, is $19 /$ hour. Determine the average waiting time in minutes. (Round your answer to TWO places of decimal) \#5.
Answers
The average waiting time in minutes is approximately 0.317 minutes.
To determine the average waiting time in minutes, we can use the queuing theory formula for average waiting time in an\($\mathrm{M} / \mathrm{M} / \mathrm{c}$\) queue:
\($$W_q=\frac{\rho^{c+1}}{c ! \cdot(1-\rho)} \cdot \frac{1}{\mu-\lambda}$$\)
Where:
\($W_q$\) is the average waiting time in the queue.
\($\rho$\) is the traffic intensity, given by $\frac{\lambda}{c \cdot \mu}$.
\($c$\) is the number of service channels (cashiers).
\($\mu$\) is the service rate (customers per hour).
\($\lambda$\) is the arrival rate (customers per hour).
Given:
\($\lambda=85.5$\)customers per hour.
\($\mu=19$\) customers per hour.
\($c=5$\) cashiers.
First, let's calculate $\rho$ :
\($$\rho=\frac{\lambda}{c \mu}=\frac{85.5}{5 \cdot 19} \approx 0.9011$$\)
Now, let's calculate \($W_q$\) :
\($$W_q=\frac{\rho^{c+1}}{c ! \cdot(1-\rho)} \cdot \frac{1}{\mu-\lambda}\\=\frac{0.9011^{5+1}}{5 ! \cdot(1-0.9011)} \cdot \frac{1}{19-85.5} \\\approx 0.317 \text { (rounded to two decimal places) }$$\)
Therefore,the average waiting time in minutes is approximately 0.317 minutes.
learn more about interest expense on
https://brainly.com/question/24057012
#SPJ11
Ulse the standard normal distribution or the f-distribution to construct a 95% confidence interval for the population meare Justify your decion, il newter distribution can bo used, explain why. Interpret the results In a randorn sample of 46 people, the mean body mass index (BMI) was 27.2 and the standard devation was 6.0f. Which distribution should be used to construct the confidence interval? Choose the correct answer below. A. Use a 1-distribuition because the sample is random, the population is normal, and σ is uricnown 8. Use a normal distribution because the sample is random, the population is normal, and o is known. C. Use a nomal distribution because the sample is random, n≥30, and α is known. D. Use a t-distribution because the sample is random, n≥30, and σ is unknown. E. Neither a normal distribution nor a t-distribution can be used because either the sample is not random, of n < 30 , and the population a nat known to be normal.
Answers
We can be 95% confident that the true population mean BMI is between 25.368 and 29.032.
A 95% confidence interval for the population mean can be constructed using the t-distribution when the sample size is small (<30) or the population standard deviation is unknown.
In this case, we have a random sample of 46 people with a mean body mass index (BMI) of 27.2 and a standard deviation of 6.0.
Thus, we need to use the t-distribution to construct the confidence interval.
The formula for the confidence interval is as follows:
Upper limit of the confidence interval:27.2 + (2.013) (6.0/√46) = 29.032Lower limit of the confidence interval:27.2 - (2.013) (6.0/√46) = 25.368
Therefore, the 95% confidence interval for the population mean BMI is (25.368, 29.032).
This means that we can be 95% confident that the true population mean BMI is between 25.368 and 29.032.
To learn more about true population visit:
https://brainly.com/question/32979836
#SPJ11
find the distance between each pair points (-4,6) and (3,-7)
Answers

May someone please help me with this question? With Step-by-step
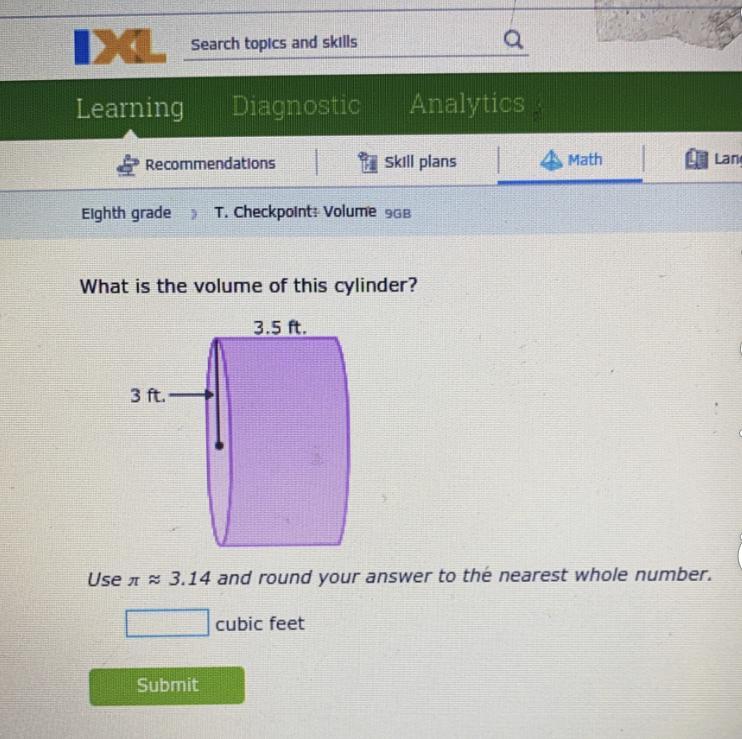
Answers
Answer:
32.92
Step-by-step explanation:
well you just do base times height
the height is 3.5
the area of the base is 3 * pi which is 9.42 if you round pi to 3.14
so 3.5*9.42= 32.92
Step by step solution: See Photo

Three more than a certain number is six less than four times
the same number. What is the number?
Answers
Answer:
number is 3
Step-by-step explanation:
let n be the number , then 3 more than the number is n + 3 and six less than 4 times the number is 4n - 6 , so
4n - 6 = n + 3 ( subtract n from both sides )
3n - 6 = 3 ( add 6 to both sides )
3n = 9 ( divide both sides by 3 )
n = 3
the number is 3
I need help! I'm almost done with my test this is one of the last questions!

Answers
Answer:
3 1/2
Step-by-step explanation:
|3 1/2|
= | 7/2|
= 7/2
= 3 1/2
help!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
x=-3
Step-by-step explanation:
-4(-2x+5)-5x+5=-24
8x-20-5x+5=-24
3x-15=-24
3x=-9
x=-3
I hope that this helped you!
How many different ways are there to get 10 heads in 20 throws of a true coin?
Answers
Now how many ways can we get 10 heads? This is 20 choose 10, or (20/10)
This means our probability is (20/10)2(20)=184756/1048576≈.1762
Select the correct answer.
Martha manages a home improvement store and uses this function to model the number of customers that visit the store each hour on a
Saturday afternoon.
n(t) = -2.82t2 + 25.746 + 60.87
Which graph would most likely be associated with this model?

Answers
The given quadratic equation gives the parameters of the shape of the
graph of the equation.
The graph that is most likely associated with the model is; graph BReasons:
The given function is n(t) = -2.82·t² + 25.74·t + 60.87
by analyzing the above function, we have;
At t = 0
n(0) = -2.82 × 0² + 25.74 × 0 + 60.87 = 60.87
The x-coordinate of the maximum point is given by \(\displaystyle x = -\frac{b}{2 \cdot a}\)
Which gives;
\(\displaystyle t = -\frac{25.74}{2 \times (-2.82)} \approx 4.564\)
The maximum value of the function is therefore;
n(4.564) = -2.82 × 4.564² + 25.74 × 4.564 + 60.87 ≈ 119.61
The characteristics of the equation are;
Initial value of equation = 60.87
t-coordinate of the maximum point, t ≈ 4.564
Maximum value of the of the function = 119.61
By comparing with the given graphs, we have;
\(\begin{tabular}{c|c|c|}&Graph A&Graph B\\Initial value&100&75\\t-value at max point&7&4\\Maximum value&200&125\end{array}\right]\)Therefore, the graph that will most likely be associated with the model is; graph B.
Learn more about graphs of quadratic equations here:
https://brainly.com/question/10989920
Answer:
The correct answer is graph B.
Step-by-step explanation:
I got it right on the Edmentum test.
What’s the quadratic function answer for 2(x^2-3x+6)
Answers
The quadratic function answer for 2(x^2-3x+6) is 4x^2 - 6x + 12.
I believe that is correct
nia is fixing a rectangular sign. She plans to place metal trim around the sign edges. The rectangle measures 64.5 cm x 18.2 cm. How much trim will nia need?
Answers
Nia needs 165.4cm trim.
What is a rectangle measure?
It has a tight, flat form. There are 4 corners, 4 angles, and 4 sides. It has length and width as its 2 dimensions. A rectangle has 90° angles on each side. The opposing sides are parallel and equal. A rectangle is a quadrilateral in which all the angles are equal and the opposite sides are equal and parallel. There are many rectangular objects around us.
Here, we have
Given: Nia is fixing a rectangular sign. She plans to place metal trim around the sign edges. The rectangle measures 64.5 cm x 18.2 cm.
P = 2*L + 2*W
L = 64.5 cm
W = 18.2 cm
P = 2*(64.5) + 2*(18.2)
P = 129+36.4
P = 165.4cm
Hence, Nia needs 165.4cm trim.
To learn more about the rectangle measure from the given link
https://brainly.com/question/22811803
#SPJ1
The number of miles a car can drive varies directly with the number of gallons of gas in
the car. If the car can go 81 miles on 3 gallons of gas, how many gallons does the car
need to go 378 miles?
Answers
Answer:
14 gallons
Step-by-step explanation:
Answer:
14 gallons
Step-by-step explanation:
a line passes through the point (-8 7) and has a slope of 5/4
Answers
Answer:
y=1.25x + 17
Coordinate, (-8,7) ==> (x,y)
Slope is 5/4 ==> 1.25
y=mx + b (m is slope)
Plug in coordinate and slope to find b
7 = 1.25(-8) + b
Multiply
7 = -10 + b
Add -10 to isolate b
17 = b
Answer:
Coordinate, (-8,7) ==> (x,y)
Slope is 5/4 ==> 1.25
y=mx + b (m is slope)
Step-by-step explanation:
anyone solve this??????????????????????????????????

Answers
Answer:
16
Step-by-step explanation:
9-9:9 +9 - 9 :9 =
9 - 1 +9 - 1 =
8 +9 - 1 =
17 - 1 =
16