Three sisters have were born in 3 consecutive years. The total of their ages is 30. What is the oldest sibling's age?
Answers
The oldest child is a 11-year-old boy.
What exactly is a sequential number?Three sisters have were born in 3 consecutive years. The total of their ages is 30.
Sequential numbers are those that follow one another continually, from lowest to biggest.
Here, assume that the youngest sibling is x years old.
Middle sibling's age will be (x+1) years old.
the oldest sibling's age is (x+2) years.
According to the inquiry,
x + (x+1) + (x+2) = 30
3x + 3 = 30
3x = 30-3
3x = 27
x = 27 / 3
x= 9
The oldest child is therefore (x + 2) years old, or 11 years old.
x+2 = 9+2 =11
The oldest child is a 11-year-old boy.
To learn more about Sequential numbers refer to:
https://brainly.com/question/23392629
#SPJ1
Related Questions
Most dietitians recommend that adults consume 20 to 30 percent of their daily caloric intake in protein. Based on this recommendation, what is the minimum amount of calories from protein an adult should consume from an 1,800 calorie diet?
Answers
Answer:
360-540 calories
the fifth term of the sequence is 5 and the sixth term is 2.5. What is the 2nd term?
Answers
Answer:
Let's denote the first term of the sequence as a, and the common difference between consecutive terms as d.
Then, we know that the fifth term is 5, so:
a + 4d = 5
Similarly, we know that the sixth term is 2.5, so:
a + 5d = 2.5
We can solve this system of equations by subtracting the first equation from the second:
(a + 5d) - (a + 4d) = 2.5 - 5
d = -2.5
Now, we can substitute this value of d into either equation to find the value of a:
a + 4d = 5
a + 4(-2.5) = 5
a - 10 = 5
a = 15
Therefore, the first term of the sequence is 15, and the common difference is -2.5. We can use this to find the value of the second term:
a + d = 15 + (-2.5) = 12.5
Therefore, the second term of the sequence is 12.5.
mark my answer as brainliest
A dragster starts from rest and accelerates at 32 m/s2m/s2. how fast is it going after tt = 4.0 secsec?
Answers
The dragster, starting from rest and accelerating at 32 m/s², reaches a speed of 128 m/s after 4.0 seconds.
A dragster starting from rest means that its initial velocity is zero. The dragster's acceleration is given as 32 m/s². To determine the speed of the dragster after 4.0 seconds, we can use the equation of motion:
where:
v = final velocity
u = initial velocity (which is 0 m/s since the dragster starts from rest)
a = acceleration (32 m/\(s^2\) in this case)
t = time (4.0 seconds in this case)
Substituting the given values into the formula:
v = 0 + (32 m/\(s^2\))(4.0 s)
v = 0 + 128 m/s
v = 128 m/s
Therefore, the dragster is traveling at a speed of 128 m/s after 4.0 seconds of acceleration.
Learn more about speed here:
https://brainly.com/question/29419608
#SPJ11
if oil leaks from a tank at a rate of r(t) gallons per minute at time t, what does 120 0 r(t) dt represent?
Answers
the total amount of oil that leaks out over the entire time interval [0, 120].
integral ∫₀¹₂₀ r(t) dt represents the total amount of oil that leaks from the tank in 120 minutes.
To see why, consider the definition of an integral. If we divide the interval [0, 120] into small subintervals of width Δt, then the amount of oil that leaks out during each subinterval is approximately r(t)Δt. Summing up all these small amounts over the entire interval gives:
Σᵢ r(tᵢ) Δt
where tᵢ is the midpoint of the i-th subinterval. As we take the limit as the subinterval width goes to zero, this sum becomes the integral:
∫₀¹₂₀ r(t) dt
which represents the total amount of oil that leaks out over the entire time interval [0, 120].
To learn more about interval click here:brainly.com/question/29179332
#SPJ11
is xsquare+1/xsquare equal5 is quadratic or not
Answers
Answer:
Yes, it is a quadratic equation.
Step-by-step explanation:
Let's solve it to make it a quadratic equation:
=> \(\frac{x^2+1}{x^2} =5\)
=> x²+1 = 5x²
=> 5x²-x²-1 = 0
=> 4x²-1 = 0
Comparing it with the standard form of quadratic equation i.e.
\(ax^2+bx+c = 0\)
So, we get
a = 4 , b = 0 and c = -1
So, yes. It is a quadratic equation and it is a pure quadratic equation since b is equal to 0.
An autonomous car is programmed to travel forty kilometers at an average speed of 40 km/hr. During the first 20 km, an average speed of 40 km/hr is maintained. During the next ten kilometers, however, the car averages only twenty km/hr. To drive the remaining ten kilometers and average 40 km/hr, the autonomous car must drive
Answers
Answer:
To cover the remaining ten kilometres and average 40 km/hr, the autonomous car must drive at infinite speed (light speed)
Step-by-step explanation:
The average speed = (The total distance)/(The total time taken)
The given parameters are;
The required average speed of the autonomous car = 40 km/hr
The average speed of the car during the first 20 km = 40 km/hr
The average speed of the car during the next 10 km = 20 km/hr
Therefore, we have;
The time taken = Distance/Speed
The time taken by the car during the first 20 km = 20 km/40 km/hr = 0.5 hour
The time taken by the car during the next 10 km = 10 km/20 km/hr = 0.5 hour
Therefore, the amount of time elapsed = 0.5 hour + 0.5 hour = 1 hour
The distance covered = 30 km
Which gives;
To drive the remaining distance of 10 km the car has 0 hour left,
The speed of the remaining 10 km must therefore be 10/0 = Infinite (speed).
To cover the remaining ten kilometres and average 40 km/hr, the autonomous car must drive at infinite speed.
The results that Charles, Isabella and Naomi achieved in four tests are shown in
the table below. They want to see who has the most consistent results.
a) Which of the mean, median, mode or range should they calculate to help
them decide?
b) Who achieved the most consistent results?
Charles 46, 43, 39, 57
Isabella
69, 64, 62, 71
Naomi
94,80, 61,72
Answers
Answer:
Range & Isabella
Step-by-step explanation:
Part A:
Definitely not range mean or median, as that'll give you their average, not consistency. None of their tables show any repeating values, so not mode either, and range would be the most hopeful for this.
Part B:
The results with the smallest range would be the most consistent:
Charles:
Lowest value = 39 and Highest Value = 57
Range = 57-39 = 18
Isabella:
Lowest value = 62 and Highest value = 71
Range = 71-62 = 9
Naomi:
Lowest value = 61 and Highest value = 94
Range = 94-61 = 33
Isabella achieved the most consistent results. Hope this helps
Megan is shopping at a store that sells jewelry, scarves, and purses. The cost of all of the items at the store includes tax. Megan buys 3 bracelets and 3 necklaces. Each bracelet costs $5. Megan pays the clerk $40 and gets $4 change. What is the cost, in dollars, of one necklace?
Answers
Answer: 7$
Step-by-step explanation: 40-4= 36 | 3x5=15 | 36-15=21 | 21/3=7
Compute the directional derivative of the function f(x,y)=y^2 ln(x) at the point (2,1) in the direction of the vector v=−3i^+j^. Enter an exact answer involving radicals as necessary.
Answers
The directional derivative is (-3/2√10) + (2 ln(2)/√10).
To compute the directional derivative of f(x,y) = y² ln(x) at the point (2,1) in the direction of the vector v = -3i + j, first find the gradient of f and then take the dot product with the unit vector in the direction of v.
The gradient of f(x, y) is given by (∂f/∂x, ∂f/∂y) = (y²/x, 2y ln(x)). At the point (2,1), this becomes (1/2, 2 ln(2)).
Next, find the unit vector of v by dividing v by its magnitude: u = v/||v|| = (-3, 1)/√((-3)² + 1²) = (-3, 1)/√10.
Now, take the dot product of the gradient and the unit vector: ((1/2, 2 ln(2)) · (-3/√10, 1/√10)) = (-3/2√10) + (2 ln(2)/√10).
To know more about directional derivative click on below link:
https://brainly.com/question/30365299#
#SPJ11
Rebecca carries a balance on her credit card each month. Today is the first day of the new. 28-day billing cycle. The current balance is x and the APR is 24%.
Rebecca is buying a friend an expensive gift that costs $1,400 that she plans to put on her credit card. This will be her only purchase this month. Sed she will be
making this purchase on the last day of the month. Part A if her finance charge will be $51 write and solve an equation to determine her current balance on her credit card show your work. Part B How much in finance charges can she save by making the purchase on the last day of the billing cycle
Answers
Part A: Rebecca's credit card balance can be calculated using the equation x = (51 - 1) 0.02 if her finance charge is $51.
Part B: By making the purchase on the final day of the billing cycle rather than the first day, Rebecca will be able to avoid paying $27 in finance charges.
How do equations work?
A mathematical statement proving the equality of values between two or more mathematical expressions is called an equation.
Equation symbols (=) are used to represent equations.
A finance charge is what?
The interest and other fees levied on credit cards are included in a finance charge.
Typically, the finance charge is based on a stated APR (annual percentage rate).
The month's billing cycle lasts for 28 days.
Balance at current starting = x.
APR = 24%, or annual percentage rate.
The monthly percentage rate (MPR) equals 2% (24% divided by 12).
The final day's purchase cost $1,400.
$51 is the total finance fee for the month.
($1,400 x 2% x 1/28) = $1 finance fee for the last-minute purchase.
$50 ($51 - $1) serves as the initial balance's finance charge.
The starting balance at this time is x = $2,500 ($50 x 2%).
Current Beginning Balance Equation: x = 51 - 1 0.02
($1,400 x 2%) Equals $28 in total loan charges for the last-minute purchase.
Finance charge savings from buying on the last day equals $27 ($28 - $1).
By buying the $1,400 gift for her friend on the last day of the billing cycle rather than the first, Rebecca can avoid paying $27 in finance charges.
Learn more about credit cards and finance charges at brainly.com/question/22717601
#SPJ4
Which of the following is equivalent to 5(4-m)-2(m+3)? *
don’t give me that link .

Answers
\(\longrightarrow{\green{Option\:1.\:(14\:-\:7m)}}\)
\(\large\mathfrak{{\pmb{\underline{\red{Step-by-step\:explanation}}{\orange{:}}}}}\)
\(5 \: (4 - m) - 2 \: (m + 3) \\ \\ = 20 - 5m - 2m - 6\)
Combining like terms, we have
\( = 20 - 6 - 5m - 2m \\ \\ = 14 - 7m\)
\(\large\mathfrak{{\pmb{\underline{\orange{Mystique35 }}{\orange{♡}}}}}\)
Which of the following is the equation of the ellipse with a vertical major axis, center at (1, -3), a = 7, and b = 5?
Answers
The equation of the ellipse with a vertical major axis, center at (1, -3), a = 7, and b = 5 is; (x - 1)²/25 + (y + 3)²/49 = 1
What is the equation of the ellipse?The general format for equation of an ellipse with center (h, k) and vertical major axis is;
(x - h)²/b² + (y - k)²/a² = 1
We are given the following;
center at (1, -3)
a = 7
b = 5
Thus;
Equation of ellipse with given parameters is;
(x - 1)²/5² + (y + 3)²/7² = 1
This simplifies to;
(x - 1)²/25 + (y + 3)²/49 = 1
Read more about Equation of Ellipse at; https://brainly.com/question/16904744
#SPJ1
help solve this as a two step equation!!

Answers
Answer:
x = - 14
Step-by-step explanation:
Step 1: Equation
x/2 - 7 = - 14
Step 2: Solve
x - 14 = - 28
Answer:
x = - 14
Hope This Helps :)
What is (f + g)(x)?
f(x) = -3x² + 3
g(x) = −3x
Answers
Answer:
Step-by-step explanation:
(f.g)(x)=\(-3*(-3x)^{2}+3=-27x^{2}+3\)
Helppppppppppppppppppppppppppppppppppppppp

Answers
Answer:
B
Step-by-step explanation:
Answer:
the answer B
Step-by-step explanation:
This sample is selected by dividing the population into subgroups and then taking a fixed number of units from each group using the simple random sample. simple random sample stratified random sample cluster random sample Voluntary random sample
Answers
The correct sampling method described in the question is a stratified random sample among the simple random sample, stratified random sample, cluster random sample and Voluntary random sample
The sampling method described in the question is a stratified random sample.
In a stratified random sample, the population is divided into subgroups or strata based on certain characteristics or criteria. Then, a random sample is selected from each stratum. The key idea behind this method is to ensure that each subgroup is represented in the sample proportionally to its size or importance in the population. This helps to provide a more accurate representation of the entire population.
In the given sampling method, the population is divided into subgroups, and a fixed number of units is taken from each group. This aligns with the process of a stratified random sample. The sample selection is random within each subgroup, but the number of units taken from each group is fixed.
Other sampling methods mentioned in the question are:
Simple random sample: In a simple random sample, each unit in the population has an equal chance of being selected. This method does not involve dividing the population into subgroups.
Cluster random sample: In a cluster random sample, the population is divided into clusters or groups, and a random selection of clusters is included in the sample. Within the selected clusters, all units are included in the sample.
Voluntary random sample: In a voluntary random sample, individuals self-select to participate in the sample. This method can introduce bias as those who choose to participate may have different characteristics than those who do not.
Therefore, the correct sampling method described in the question is a stratified random sample.
Learn more about sampling methods here:
https://brainly.com/question/15604044
#SPJ4
A parabola is defined as the set of points the same distance from (6,2) and line y=4. Select all points that are on this parabola
Answers
In conclusion there are no points among the given options that are on the parabola.
why it is?
The vertex of the parabola is the midpoint between the point (6, 2) and the line y = 4, which is at (6, 3). Since the focus is below the vertex and the directrix is a horizontal line, the equation of the parabola is of the form:
(x - h)²2 = 4p(y - k)
where (h, k) is the vertex and p is the distance from the vertex to the focus (and from the vertex to the directrix).
Using the vertex and the given point (6, 2), we can find that p = 1. Therefore, the equation of the parabola is:
(x - 6)²2 = 4(y - 3)
Now we can check which of the given points satisfy this equation:
A. (4, 6)
(4 - 6)²2 = 4(6 - 3)
4 = 12 - 12
This point is not on the parabola.
B. (5, 7)
(5 - 6)²2 = 4(7 - 3)
1 = 16
This point is not on the parabola.
C. (6, 5)
(6 - 6)²2 = 4(5 - 3)
0 = 8
This point is not on the parabola.
D. (7, 6)
(7 - 6)²2 = 4(6 - 3)
1 = 12
This point is not on the parabola.
E. (8, 5)
(8 - 6)²2 = 4(5 - 3)
4 = 8
This point is not on the parabola.
Therefore, there are no points among the given options that are on the parabola.
To know more about Parabola related questions, visit:
https://brainly.com/question/21685473
#SPJ1
Complete question:
Which points are on the parabola defined as the set of points the same distance from (6,2) and the line y=4?
A box has the shape of a rectangular prism with height 30 cm. If the height is increased by 0.2 cm, by how much does the surface area of the box increase?
Answers
If the height is increased by 0.2 then the surface area will be increased by 1.14times the original.
What is surface area of a prism?A prism is a solid shape that is bound on all its sides by plane faces.
The surface area of a prism is expressed as;
SA = 2B + ph
where h is the height , p is the perimeter of the base and B is the base area
The scale factor in terms of height = 32/30
if x is the surface area of old prism and y for new
then area factor = (16/15)² = 256/225
256/225 = y/x
225y = 256x
y = 256/225 x
y = 1.14x
therefore the surface area will increase by 1.14times the original.
learn more about surface area from
https://brainly.com/question/16519513
#SPJ1
The sum of 110 and a number
is five times that number
minus 10. What is the
number?
Answers
Answer: Let the number = x
5x+10 = 120
Or, 5x = 120 - 10
Or, 5x = 110
Or, x = 110/5
Or, x = 2
Step-by-step explanation:
If B is the midpoint of AC and AB = 5 Find BC and AC.
Answers
The length of BC is 5
The length of AC is 10
Midpoint of a line: Calculating length of a lineFrom the given information, we are to calculate the length of the given parts of line AC
From the given information,
B is the midpoint of AC
Thus,
We can write that
AB + BC = AC
and
AB = BC
Also, from the given information,
AB = 5
Therefore,
BC = 5
From the equation,
AB + BC = AC
Substitute the values of AB and BC
5 + 5 = AC
10 = AC
AC = 10
Hence, BC = 5 and AC = 10
Learn more on Midpoint of a line: Calculating length of a line here: https://brainly.com/question/26034806
#SPJ1
HELP PLEASE!!!!dont answer just for points:(

Answers
Answer:
15 is 50% of 30
and 75% of 20
Which transformation maps quadrilateral EFGH onto JKLM?
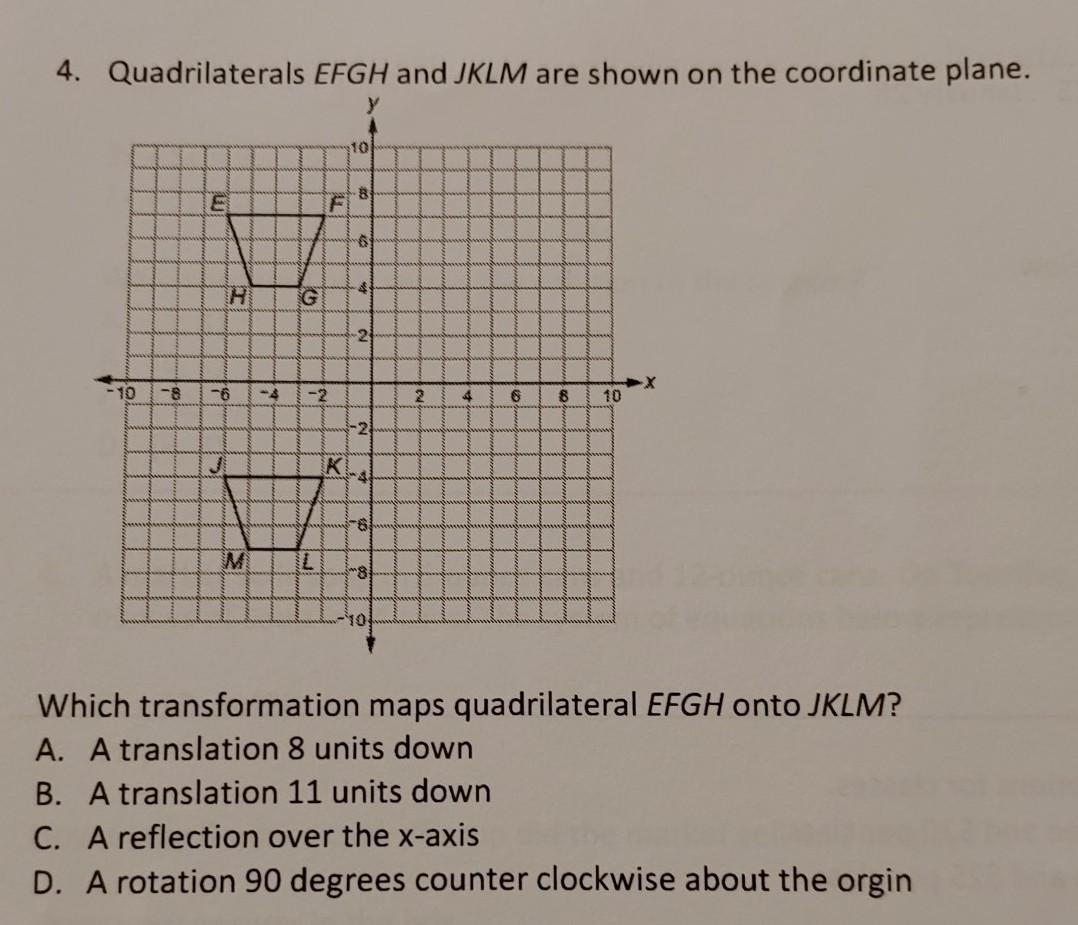
Answers
Answer:
A) A translation 8 units down
Step-by-step explanation:
It does not reflect over the x-axis because it would have flip.
Not 11 units down, only 8
it did not rotate 90 degrees, it went a little more past that
find the area between a large loop and the enclosed small loop of the curve r = 2 + 4 cos(3θ).
Answers
Therefore, the area between the large loop and the small loop of the curve r = 2 + 4cos(3θ) is 70π/3.
To find the area between the large loop and the small loop of the curve, we need to find the points of intersection of the curve with itself.
Setting the equation of the curve equal to itself, we have:
2 + 4cos(3θ) = 2 + 4cos(3(θ + π))
Simplifying and solving for θ, we get:
cos(3θ) = -cos(3θ + 3π)
cos(3θ) + cos(3θ + 3π) = 0
Using the sum to product formula, we get:
2cos(3θ + 3π/2)cos(3π/2) = 0
cos(3θ + 3π/2) = 0
3θ + 3π/2 = π/2, 3π/2, 5π/2, 7π/2, ...
Solving for θ, we get:
θ = -π/6, -π/18, π/6, π/2, 5π/6, 7π/6, 3π/2, 11π/6
We can see that there are two small loops between θ = -π/6 and π/6, and two large loops between θ = π/6 and π/2, and between θ = 5π/6 and 7π/6.
To find the area between the large loop and the small loop, we need to integrate the area between the curve and the x-axis from θ = -π/6 to π/6, and subtract the area between the curve and the x-axis from θ = π/6 to π/2, and from θ = 5π/6 to 7π/6.
Using the formula for the area enclosed by a polar curve, we have:
A = 1/2 ∫[a,b] (r(θ))^2 dθ
where a and b are the angles of intersection.
For the small loops, we have:
A1 = 1/2 ∫[-π/6,π/6] (2 + 4cos(3θ))^2 dθ
Using trigonometric identities, we can simplify this to:
A1 = 1/2 ∫[-π/6,π/6] 20 + 16cos(6θ) + 8cos(3θ) dθ
Evaluating the integral, we get:
A1 = 10π/3
For the large loops, we have:
A2 = 1/2 (∫[π/6,π/2] (2 + 4cos(3θ))^2 dθ + ∫[5π/6,7π/6] (2 + 4cos(3θ))^2 dθ)
Using the same trigonometric identities, we can simplify this to:
A2 = 1/2 (∫[π/6,π/2] 20 + 16cos(6θ) + 8cos(3θ) dθ + ∫[5π/6,7π/6] 20 + 16cos(6θ) + 8cos(3θ) dθ)
Evaluating the integrals, we get:
A2 = 80π/3
Therefore, the area between the large loop and the small loop of the curve r = 2 + 4cos(3θ) is:
A = A2 - A1 = (80π/3) - (10π/3) = 70π/3
To know more about area,
https://brainly.com/question/31479047
#SPJ11
Help with this equation I need to turn it in

Answers
Answer:
y=12x+40
Step-by-step explanation:
The earnings are the initial payment per month plus the pay per hour times the number of hours.
How do i find the slope and y intercept?

Answers
Answer:
The slope is the change in y over the change in x.
Look at the g(x) and the x. \(\frac{2 - (-4) }{0 - (-12)}\) = \(\frac{6}{12}\) = \(\frac{1}{2}\). The slope is 1/2
The y intercept is when x is zero. So the point (0,2) is the intercept. We say that the y intercept is 2. That is where the line will cross the y axis.
Step-by-step explanation:
Please help I’m so stressed over this ok here it is it cost $12.50 to enter an amusement park and $1.50 to play each game. Solve an inequality to find the number of games, g, Cole can play if he has $35 to spend at the park. Enter your answer in the box.
Answers
He can go on 15 gams
i need help on this and yea

Answers
Answer:
3
Step-by-step explanation:
(Q2) The set of line segments _____ meet the requirements to form a triangle.8 cm4 cm3 cm
Answers
To form a triangle, the set of line segments must satisfy the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. Therefore, we need to check if the given line segments 8 cm, 4 cm, and 3 cm meet this requirement.
We can start by checking if the sum of the two smaller sides (3 cm and 4 cm) is greater than the largest side (8 cm). 3 cm + 4 cm = 7 cm, which is less than 8 cm. Therefore, these three line segments cannot form a triangle.
In general, for a set of line segments to form a triangle, the largest side must be smaller than the sum of the other two sides. In this case, the line segment of 8 cm is too long compared to the other two sides, which makes it impossible to form a triangle.
In conclusion, there are no line segments that meet the requirements to form a triangle with lengths of 8 cm, 4 cm, and 3 cm.
learn more about the inequality theorem here: brainly.com/question/1163433
#SPJ11
if the average (arithmetic mean) of 24 consecutive odd integers is 48, what is the median of the 24 numbers?
Answers
Answers: 36
Step-by-step explanation:
Tammy estimated the product of 4.2 and 5.9, then calculated the exact product. Analyze her work and decide if she made an error.
Answers
Answer:
C.Tammy’s estimate is right, but the actual product should be 24.78.
Step-by-step explanation:
i took the assessment! thank you for your attention and i hope i helped!!
Answer:
the answer is C which is Tammy’s estimate is right, but the actual product should be 24.78.
Step-by-step explanation: