Three-quarters of a number is 15.
Work out four-fifths of the number.
Answers
Answer:
16
Step-by-step explanation:
let the number be x , then
\(\frac{3}{4}\) x = 15 ( multiply both sides by 4 to clear the fraction )
3x = 60 ( divide both sides by 3 )
x = 20 , then
\(\frac{4}{5}\) × 20 = 4 × 4 = 16
Answer:
16
Step-by-step explanation:
let the number be x , then
\frac{3}{4} x = 15 ( multiply both sides by 4 to clear the fraction )
3x = 60 ( divide both sides by 3 )
x = 20 , then
\frac{4}{5} × 20 = 4 × 4 = 16
Related Questions
what function lets you test if something is true or false and then do different things depending on which result you get?
Answers
The function that lets you test if something is true or false and then do different things depending on which result you get is called an "if statement".
In programming, an if statement is a conditional statement that allows you to execute certain code if a specified condition is true, and a different set of code if the condition is false. The syntax for an if statement typically involves the use of a comparison operator (such as "==" for equality or ">" for greater than) to compare a variable or expression to a specific value or set of values. If the comparison evaluates to true, the code inside the if statement is executed. If the comparison evaluates to false, the code inside the if statement is skipped and the program moves on to the next line of code. If statements can also be combined with other statements, such as else statements or nested if statements, to create more complex logic in a program.
Learn more about syntax here:
https://brainly.com/question/11364251
#SPJ11
Select the correct answer. The dot product between the vectors \[ u=a i+b j, \quad v=i-b j \] is \[ a-b^{2} \] \( a^{2}-b^{2} \) \[ b-a \] \( a-b \) \( a^{2}-b \)
Answers
The dot product between the vectors \( u = a\mathbf{i} + b\mathbf{j} \) and \( v = \mathbf{i} - b\mathbf{j} \) is \( a^2 - b^2 \).
To find the dot product between two vectors, we multiply their corresponding components and then sum them up.
Let's calculate the dot product between \( u \) and \( v \):
\( u \cdot v = (a\mathbf{i} + b\mathbf{j}) \cdot (\mathbf{i} - b\mathbf{j}) \)
Expanding the dot product, we have:
\( u \cdot v = a\mathbf{i} \cdot \mathbf{i} + a\mathbf{i} \cdot (-b\mathbf{j}) + b\mathbf{j} \cdot \mathbf{i} + b\mathbf{j} \cdot (-b\mathbf{j}) \)
Since \( \mathbf{i} \) and \( \mathbf{j} \) are orthogonal unit vectors, their dot products with themselves are equal to 1, and their dot product with each other is equal to 0:
\( \mathbf{i} \cdot \mathbf{i} = 1 \)
\( \mathbf{i} \cdot \mathbf{j} = 0 \)
\( \mathbf{j} \cdot \mathbf{j} = 1 \)
Simplifying the dot product of \( u \) and \( v \):
\( u \cdot v = a(1) + a(0) + b(0) + b(1) = a + b \)
Therefore, the dot product between u and v is a + b.
To learn more about vectors, click here: brainly.com/question/17157624
#SPJ11
Solve for x: 2/7 (x - 2) = 4x
(9th grade Algebra 1)
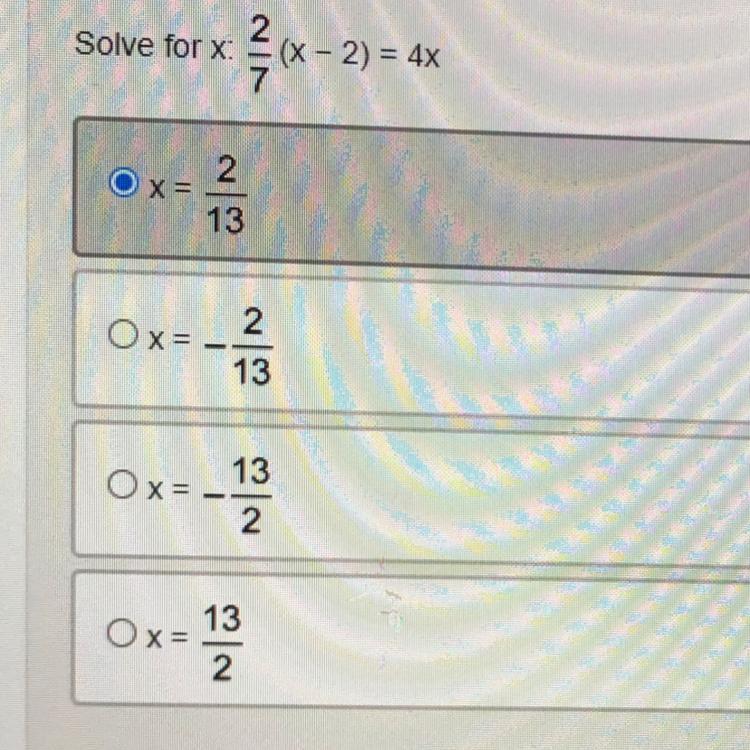
Answers
Pls mark as brainest if it was the best
Have a lovely day

Asx approaches negative infinity, for which of the following functions does f(x) approach positive infinity? Select all that apply. Select all that apply: f(x) =2x5 Ofx)9x +100 f(x)= 6x8 +9x6+32 f(x)=-8x3 + 11 f(x)=-10x +5x+ 26 f(x)=-x +8x4 + 248
Answers
Among the provided functions, the ones that approach positive infinity as x approaches negative infinity are:
- f(x) = 2x^5
- f(x) = 6x^8 + 9x^6 + 32
- f(x) = -x + 8x^4 + 248
To determine which functions approach positive infinity as x approaches negative infinity, we need to analyze the leading terms of the functions. The leading term dominates the behavior of the function as x becomes very large or very small.
Let's examine each function and identify their leading terms:
1. f(x) = 2x^5
The leading term is 2x^5, which has a positive coefficient and the highest power of x.
As x approaches negative infinity, this term becomes very large and positive, indicating that f(x) approaches positive infinity.
2. f(x) = 9x + 100
The leading term is 9x, which has a positive coefficient but a lower power of x compared to the constant term 100.
As x approaches negative infinity, the leading term becomes very large and negative, indicating that f(x) approaches negative infinity, not positive infinity.
3. f(x) = 6x^8 + 9x^6 + 32
The leading term is 6x^8, which has a positive coefficient and the highest power of x.
As x approaches negative infinity, this term becomes very large and positive, indicating that f(x) approaches positive infinity.
4. f(x) = -8x^3 + 11
The leading term is -8x^3, which has a negative coefficient and the highest power of x.
As x approaches negative infinity, this term becomes very large and negative, indicating that f(x) approaches negative infinity, not positive infinity.
5. f(x) = -10x + 5x + 26
Combining like terms, we have f(x) = -5x + 26.
The leading term is -5x, which has a negative coefficient but a lower power of x compared to the constant term 26.
As x approaches negative infinity, the leading term becomes very large and positive, indicating that f(x) approaches negative infinity, not positive infinity.
6. f(x) = -x + 8x^4 + 248
The leading term is 8x^4, which has a positive coefficient and the highest power of x.
As x approaches negative infinity, this term becomes very large and positive, indicating that f(x) approaches positive infinity.
Therefore, the correct choices are:
- f(x) = 2x^5
- f(x) = 6x^8 + 9x^6 + 32
- f(x) = -x + 8x^4 + 248
To know more about functions refer here:
https://brainly.com/question/28134738#
#SPJ11
For anything more then 50% there is no cure. If the disease is spreading according to the formula P=6d+5 where P is the percent of the body affected and d is the number of days, fill out the following chart and explain to a patient what you observed. Days % of hods Affected

Answers
Disease spreading formula
\(P=6d+5\)Where d = number of days
Now, we need to calculate the value of P for the different days
Day 1
P = 6*(1)+5 = 11%
Day 2
P = 6*(2)+5 = 17%
Day 3
P = 6*(3)+5 = 23%
Day 4
P = 6*(4)+5 = 29%
Day 5
P = 6*(5)+5 = 35%
Day 6
P = 6*(6)+5 = 41%
Day 7
P = 6*(7)+5 = 47%
Day 8
P = 6*(8)+5 = 5353%
The disease starts spreading from day 1 and continues to increase day after day in a linear fashion. After day 8 there is no cure for the disease as it exceeds 50%.
Find the mean and median of each data set.
The average yearly gold price for the period from 2000-2009:
$279.11, $271.04, $309.73, $363.38, $409.72, $444.74, $603.46,
$695.39, $871.96, $972.35
Answers
Answer:
Median: $427.23
Mean: $522.09
Step-by-step explanation:
271.04, 279.11, 309.73, 363.38, 409.72, 444.74, 603.46, 695.39, 871.96, 972.35
simplify the following expression -2a- (-3+a^2)
Answers
Answer is in the image
Step-by-step explanation:
Sorry if wrong or blurry

Kindly help me solve this questions
a) 3/X+2-2=1/1/2
b) 3(4-7x)/5-0.7=x-6/2
Answers
Answer:
a) x=6
b) x= 498/463
hope this helps!!
Find area of the shaded
segment.

Answers
The area of the shaded segment is 7.125 cm²
How to find the area of the shaded segment?The area of the shaded segment will be equal to the difference between the area of a quarter of a circle of radius R = 5cm, and a right triangle whose two legs measure 5cm.
The area of the quarter circle is:
A = (1/4)*3.14*(5cm)²
A = 19.625 cm²
And the area of the triangle is:
a = 5cm*5cm/2 = 12.5 cm²
Then the area of the shaded figure is:
A - a = 19.625 cm² - 12.5 cm²
A - a = 7.125 cm²
Learn more about area at:
https://brainly.com/question/24487155
#SPJ1
PLEASE HELP ASAP!!!-
And the number is ______
a number formed with straight lines only.
a number with only one of its digits are greater than 4.
a 2-digit odd number.
a number found as the date each month on the calendar.
Answers
Answer:
43
Step-by-step explanation:
I think if I am wrong so sorry
a coin is flipped 300 times heads is 286 tail 14 times.
what is the probability it will be tails?
Answers
the probability of getting tails when flipping the coin is approximately 0.0467 or 4.67%.
To find the probability of getting tails when flipping a coin, we need to divide the number of desired outcomes (tails) by the total number of possible outcomes.
In this case, the coin is flipped 300 times, and tails is observed 14 times. So the probability of getting tails on any given flip is:
Probability of tails = Number of tails / Total number of flips
Probability of tails = 14 / 300
Simplifying this fraction, we get:
Probability of tails = 0.0467
To know more about number visit:
brainly.com/question/3589540
#SPJ11
Plllllllease helpppppp

Answers
Answer:
Step-by-step explanation:
b/c we know that these triangles both have equal sides... that is given that ab and be are the same length. and that be and cd are parallel , we know that they both are isosceles triangles and that the base angles are the same. The side on ad and ae have equal angles.
so we can make the equation
2a +56 = 180 (b/c we know that around a triangle it's 180°
2 a = 124
a = 62
so ∠ BAE = 62°
:)
Median of 5,8,11,8,3,2,4,6,9,8
Answers
Answer:
8
Step-by-step explanation:
is the median
give email id
2,3,4,5,6,8,8,8,9,11
Then get the middle numbers which are 6 and 8 then add it and devide by 2
6+8/2=14/2
=7
I hope this was helpful pls mark answer as brainest answer if it was the best
Pls have a nice day
A polygon has 10080degree as the total interior angle how many sides has the polygon a. 48 b. 58. C. 40
D. 32
Answers
Answer:
B
Step-by-step explanation:
the sum of the interior angles of a polygon is
sum = 180° ( n - 2) ← n is the number of sides
given sum = 10080 , then
180° (n - 2) = 10080 ( divide both sides by 180 )
n - 2 = 56 ( add 2 to both sides )
n = 58
that is the polygon has 58 sides
I need help with this asap please!!!

Answers
Answer:
54
Step-by-step explanation:
54x
Represent the following sentence as an algebraic expression, where "a number" is the letter x. You do not need to simplify. 7 minus the cube of a number.
Answers
The algebraic expression which correctly represents the word phrase; 7 minus the cube of a number as given in the task content is; 7 - x³.
What is the algebraic expression which correctly represents the word phrase; 7 minus the cube of a number as given in the task content?It follows from the task content that the algebraic expression which correctly represents the word phrase; 7 minus the cube of a number as given in the task content be determined.
On this note, since the number in discuss is given and represented by; x in the task content. Hence, the cube of the number is; x³.
The word phrase; 7 minus the cube of a number can therefore be represented as;
7 - x³.
Ultimately, the algebraic expression which correctly represents the word phrase; 7 minus the cube of a number as given in the task content is; 7 - x³.
Read more on word phrase representation;
https://brainly.com/question/28221777
#SPJ1
Which equation represents a line that passes through (5’1) and has a slope of 1/2?

Answers
Answer:
third one passes through the slope .
Answer:
Step-by-step explanation:
y - 1 = 1/2(x - 5)
y - 1 = 1/2x - 5/2
y - 2/2 = 1/2x - 5/2
y = 1/2x - 3/2
Option 3
Ember is working on a project. She has a 12 inch peice of rope that she needs to cut into 1/4 pieces. How many 1/4 inch pieces can she cut from the 12 inch rope
Answers
Ember can cut a total of 48 1/4 inch pieces from the 12 inch rope.
Ember is working on a project that requires her to cut a 12-inch piece of rope into smaller pieces. Specifically, she needs to cut the rope into 1/4 inch pieces.
In order to determine how many 1/4 inch pieces Ember can cut from the 12 inch rope, we need to use division.
First, we need to convert 1/4 inches to a decimal. To do this, we divide 1 by 4:
1 ÷ 4 = 0.25
This tells us that each 1/4 inch piece is 0.25 inches long.
Next, we divide the length of the rope (12 inches) by the length of each 1/4 inch piece (0.25 inches):
12 ÷ 0.25 = 48
This means that Ember can cut 48 1/4 inch pieces from the 12 inch rope.
To learn more about inch, visit:
https://brainly.com/question/20796404
#SPJ11
Which measurement could be a surface area measure?
64.5 m 3
50 g
18 ft.
27.9 mm 2
Answers
The measurement that could be a surface area measure is D. 27.9 mm². The unit "mm²" represents square millimeters, which is a measurement of surface area.
What is a surface area?A surface area is the measurement of the outside area of an object or shape.
A surface area usually measures the surfaces of an object like the sides, top, and bottom.
It is measured in square units like square inches or square meters.
It is an important concept that is used in different areas like geometry (like a cone, cylinder, rectangular prism, etc.), physics, and engineering.
Learn more about surface area at brainly.com/question/951562
#SPJ1
Write the equation of a sine or cosine function to describe the graph.
Please help me I WILL MARK YOU AS A BRILLIANT

Answers
Answer(s):
\(\displaystyle y = 3cos\:(2\pi{x} - \frac{\pi}{2}) + 3 \\ y = -3sin\:(2\pi{x} \pm \pi) + 3 \\ y = 3sin\:2\pi{x} + 3\)
Step-by-step explanation:
\(\displaystyle y = Acos(Bx - C) + D \\ \\ Vertical\:Shift \hookrightarrow D \\ Horisontal\:[Phase]\:Shift \hookrightarrow \frac{C}{B} \\ Wavelength\:[Period] \hookrightarrow \frac{2}{B}\pi \\ Amplitude \hookrightarrow |A| \\ \\ Vertical\:Shift \hookrightarrow 3 \\ Horisontal\:[Phase]\:Shift \hookrightarrow \frac{C}{B} \hookrightarrow \boxed{\frac{1}{4}} \hookrightarrow \frac{\frac{\pi}{2}}{2\pi} \\ Wavelength\:[Period] \hookrightarrow \frac{2}{B}\pi \hookrightarrow \boxed{1} \hookrightarrow \frac{2}{2\pi}\pi \\ Amplitude \hookrightarrow 3\)
OR
\(\displaystyle y = Asin(Bx - C) + D \\ \\ Vertical\:Shift \hookrightarrow D \\ Horisontal\:[Phase]\:Shift \hookrightarrow \frac{C}{B} \\ Wavelength\:[Period] \hookrightarrow \frac{2}{B}\pi \\ Amplitude \hookrightarrow |A| \\ \\ Vertical\:Shift \hookrightarrow 3 \\ Horisontal\:[Phase]\:Shift \hookrightarrow 0 \\ Wavelength\:[Period] \hookrightarrow \frac{2}{B}\pi \hookrightarrow \boxed{1} \hookrightarrow \frac{2}{2\pi}\pi \\ Amplitude \hookrightarrow 3\)
You will need the above information to help you interpret the graph. First off, keep in mind that although this looks EXACTLY like the sine graph, if you plan on writing your equation as a function of cosine, then there WILL be a horisontal shift, meaning that a C-term will be involved. As you can see, the photograph on the right displays the trigonometric graph of \(\displaystyle y = 3cos\:2\pi{x} + 3,\) in which you need to replase "sine" with "cosine", then figure out the appropriate C-term that will make the graph horisontally shift and map onto the sine graph [photograph on the left], accourding to the horisontal shift formula above. Also keep in mind that the −C gives you the OPPOCITE TERMS OF WHAT THEY REALLY ARE, so you must be careful with your calculations. So, between the two photographs, we can tell that the cosine graph [photograph on the right] is shifted \(\displaystyle \frac{1}{4}\:unit\)to the left, which means that in order to match the sine graph [photograph on the left], we need to shift the graph FORWARD \(\displaystyle \frac{1}{4}\:unit,\)which means the C-term will be positive, and by perfourming your calculations, you will arrive at \(\displaystyle \boxed{\frac{1}{4}} = \frac{\frac{\pi}{2}}{2\pi}.\)So, the cosine graph of the sine graph, accourding to the horisontal shift, is \(\displaystyle y = 3cos\:(2\pi{x} - \frac{\pi}{2}) + 3.\)Now, with all that being said, in this case, sinse you ONLY have a graph to wourk with, you MUST figure the period out by using wavelengths. So, looking at where the graph hits \(\displaystyle [-\frac{1}{4}, 0],\)from there to \(\displaystyle [\frac{3}{4}, 0],\)they are obviously \(\displaystyle 1\:unit\)apart, telling you that the period of the graph is \(\displaystyle 1.\)Now, the amplitude is obvious to figure out because it is the A-term, but of cource, if you want to be certain it is the amplitude, look at the graph to see how low and high each crest extends beyond the midline. The midline is the centre of your graph, also known as the vertical shift, which in this case the centre is at \(\displaystyle y = 3,\)in which each crest is extended three units beyond the midline, hence, your amplitude. So, no matter how far the graph shifts vertically, the midline will ALWAYS follow.
I am delighted to assist you at any time.


Please help!!!!!!!!!!

Answers
Answer:
2/25 of the dogs.
Step-by-step explanation:
Two of the dogs are fed only dry food, and there are 25 dogs, so the answer is 2/25.
Owino gets paid 280 per week plus 5% commission on all sales for selling electronic
Answers
Answer:
what is the question?
Step-by-step explanation:
i don't see a problem or answer choices
What is the value of n

Answers
Answer:
1.5x10^-18
Step-by-step explanation:
8.4x10^9 / x = 5.6x10^27
You could make a proportion:
x(5.6 x 10^27)= 8.4x10^9
divide both sides by 5.6x10^27
x=1.5x10^-18
Answer:
\(1.5*10^{-18}\)
Step-by-step explanation:
The question is in the format \(\frac{8.4*10^9}{n}=5.6*10^{27}\)
First multiply both sides by n and then divide both sides by the number in scientific notation on the right.
\(\frac{8.4*10^9}{5.6*10^{27}}=n\)
We can think of this problem as \(\frac{8.4}{5.6}*\frac{10^{9}}{10^{27}}=\frac{8.4}{5.6}*10^9*10^{-27}\)
When dividing like-terms, we subtract their powers (or we can get the multiplicative inverse and add the powers).
We end up with \(1.5*10^{-18}\)
Exercise 10
You randomly choose one of the tiles. Without replacing the first tile, you choose a second tile. What is the probability of the compound event? Write your answer as a fraction or percent rounded to the nearest tenth.

Answers
The probability of choosing a 5 and then a 6 is 1/49
Finding the probability of the compound eventFrom the question, we have the following parameters that can be used in our computation:
The tiles
Where we have
Total = 7
The probability of choosing a 5 and then a 6 is
P = P(5) * P(6)
So, we have
P = 1/7 * 1/7
Evaluate
P = 1/49
Hence, the probability of choosing a 5 and then a 6 is 1/49
Read more about probability at
https://brainly.com/question/31649379
#SPJ1
Question
You randomly choose one of the tiles. Without replacing the first tile, you choose a second tile. Find the probability of the compound event. Write your answer as a fraction or percent rounded to the nearest tenth. The probability of choosing a 5 and then a 6
Evaluate y + (x2 + y) when x = 0.4, y = 3, z =
Answers
Answer:
6.16 is the answer
Step-by-step explanation:
3 + (.4^2 + 3)
3 + 3.16
6.16
The graph of y = |x is the solid black graph below. Which function represents the
dotted graph?

Answers
Answer:
y = |x+3| + 1
Step-by-step explanation:
The solid black graph represents the function y = |x|. Its vertex is at (0, 0).
In comparison, the light-colored graph vertex is 3 units to the left and 1 unit up. Thus, the original y = |x| becomes y = |x+3| + 1
Please Help me :)))))))))))

Answers
Answer:
35
Step-by-step explanation:
if GFL = 34 and GEL = 36 FLG would be 35
The minimum turning point
of a quadratic curve is (10,
-5).
Write an equation for this in
the form:
y=x2 + ax + b.
-
Answers
Answer:
\(y=x^2-20x+95\)
Step-by-step explanation:
Write the equation in vertex form and evaluate
\(y=(x-h)^2+k\\\\y=(x-10)^2-5\\\\y=x^2-20x+100-5\\\\y=x^2-20x+95\)
This is because the minimum (or maximum) of a quadratic curve is its vertex and \((h,k)\) is the vertex in the formula I used
Find an equation of the form y = ax² + bx+c for the parabola that goes through the points (8, 230), (-5, 48) and (3, – 40).
Answers
An equation of the form y = ax² + bx + c for the parabola that goes through the points (8, 230), (-5, 48), and (3, -40) is: y = 4.8085x² - 1.383x - 66.840
To find an equation of the form y = ax² + bx + c for the parabola that goes through the points (8, 230), (-5, 48), and (3, -40), we can use the method of solving a system of equations. Let's substitute the x and y values from each point into the equation: For the point (8, 230): 230 = a(8)² + b(8) + c (Equation 1). For the point (-5, 48): 48 = a(-5)² + b(-5) + c (Equation 2). For the point (3, -40): -40 = a(3)² + b(3) + c (Equation 3). Now, we have a system of three equations with three unknowns (a, b, c). We can solve this system to find the values of a, b, and c.
Simplifying Equation 1: 64a + 8b + c = 230. Simplifying Equation 2: 25a - 5b + c = 48. Simplifying Equation 3: 9a + 3b + c = -40. We can solve this system of equations using various methods such as substitution, elimination, or matrix methods. Let's use the elimination method to solve this system. Subtracting Equation 2 from Equation 1, we get: 39a + 13b = 182 (Equation 4), Subtracting Equation 3 from Equation 2, we get:
16a - 8b = 88 (Equation 5). Now, we have a system of two equations with two unknowns. Solving this system gives us the values of a and b.
Multiplying Equation 4 by 2, we get: 78a + 26b = 364 (Equation 6), Adding Equation 5 and Equation 6, we get 94a = 452. Dividing both sides by 94, we find: a = 452 / 94, a ≈ 4.8085. Substituting the value of a back into Equation 5, we get: 16(4.8085) - 8b = 88, b ≈ -1.383. Now that we have the values of a and b, we can substitute them into any of the original equations (Equation 1, Equation 2, or Equation 3) to find the value of c.
Using Equation 1: 64(4.8085) + 8(-1.383) + c = 230, 307.904 - 11.064 + c = 230, c ≈ -307.904 + 11.064 + 230, c ≈ -66.840. Therefore, an equation of the form y = ax² + bx + c for the parabola that goes through the points (8, 230), (-5, 48), and (3, -40) is: y = 4.8085x² - 1.383x - 66.840
To learn more about system of equations, click here: brainly.com/question/14616611
#SPJ11
A teacher wanted to determine the effectiveness of two different learning tools—a computer program or a hands-on approach—for a particular concept she was preparing to teach. She will assign her students to one of the two methods to spend the whole class time to learn this concept.
Which of the following variables would be moderated due to random assignment?
A. the teacher
B. time spent in class
C. computer experience
D. the different learning tools
Answers
Answer:
D
Step-by-step explanation: