This was on my homework 5 X-5 = 5x+7
Answers
Answer:
No solution
Step-by-step explanation:
Original Equation:
5x - 5 = 5x + 7
Add 5 to both sides
5x = 5x + 12
So we already know that this equation is not true, making it no solution
Hope this helped
Related Questions
someone please answer this
(I attached an image with the question)

Answers
Answer:
A
Step-by-step explanation:
Group like-terms, that is move the numbers to one side of the sign.
Then, divide both sides by 2

A small hotel in central London has 8 rooms. Based on data collected over the last five years, it was estimated that the probability a room is occupied on any particular "weekend" night (Saturday and Sunday) is 0.75. This is the probability of success. On any particular "weekend" night, a hotel is only occupied (Success) or not occupied (Failure). There are no other possibilities. Required: What is the probability that at least 4 of the 7 hotel rooms are occupied on any weekend night? Note: Show all your calculations in well laid-out Excel spreadsheet tables with clear headings and include formulas. Give your answers correct to 3 decimal places.
Answers
Based on the given data, the probability of a room being occupied on any particular weekend night is 0.75. To calculate the probability that at least 4 out of the 7 rooms are occupied on a weekend night, we can use the binomial probability formula. By summing up the probabilities for 4, 5, 6, and 7 occupied rooms, we find that the probability is approximately 0.923.
To calculate the probability, we can use the binomial probability formula, which states that the probability of getting exactly k successes in n independent Bernoulli trials, each with a probability p of success, is given by the formula:
P(X = k) = (n choose k) * p^k * (1 - p)^(n - k)
In this case, we want to find the probability of at least 4 out of 7 rooms being occupied on a weekend night. We can calculate this by summing up the probabilities of getting 4, 5, 6, and 7 occupied rooms.
For 4 occupied rooms:
P(X = 4) = (7 choose 4) * 0.75^4 * (1 - 0.75)^(7 - 4) = 0.339
For 5 occupied rooms:
P(X = 5) = (7 choose 5) * 0.75^5 * (1 - 0.75)^(7 - 5) = 0.395
For 6 occupied rooms:
P(X = 6) = (7 choose 6) * 0.75^6 * (1 - 0.75)^(7 - 6) = 0.266
For 7 occupied rooms:
P(X = 7) = (7 choose 7) * 0.75^7 * (1 - 0.75)^(7 - 7) = 0.122
To find the probability of at least 4 occupied rooms, we sum up the probabilities for 4, 5, 6, and 7 occupied rooms:
P(X >= 4) = P(X = 4) + P(X = 5) + P(X = 6) + P(X = 7) = 0.339 + 0.395 + 0.266 + 0.122 = 0.923
Therefore, the probability that at least 4 out of the 7 hotel rooms are occupied on any weekend night is approximately 0.923, or 92.3% when rounded to three decimal places.
Learn more about probability here: brainly.com/question/32117953
#SPJ11
Based on the given data, the probability of a room being occupied on any particular weekend night is 0.75.
To calculate the probability that at least 4 out of the 7 rooms are occupied on a weekend night, we can use the binomial probability formula. By summing up the probabilities for 4, 5, 6, and 7 occupied rooms, we find that the probability is approximately 0.923.
To calculate the probability, we can use the binomial probability formula, which states that the probability of getting exactly k successes in n independent Bernoulli trials, each with a probability p of success, is given by the formula:
P(X = k) = (n choose k) * p^k * (1 - p)^(n - k)
In this case, we want to find the probability of at least 4 out of 7 rooms being occupied on a weekend night. We can calculate this by summing up the probabilities of getting 4, 5, 6, and 7 occupied rooms. For 4 occupied rooms:
P(X = 4) = (7 choose 4) * 0.75^4 * (1 - 0.75)^(7 - 4) = 0.339
For 5 occupied rooms:
P(X = 5) = (7 choose 5) * 0.75^5 * (1 - 0.75)^(7 - 5) = 0.395
For 6 occupied rooms:
P(X = 6) = (7 choose 6) * 0.75^6 * (1 - 0.75)^(7 - 6) = 0.266
For 7 occupied rooms:
P(X = 7) = (7 choose 7) * 0.75^7 * (1 - 0.75)^(7 - 7) = 0.122
To find the probability of at least 4 occupied rooms, we sum up the probabilities for 4, 5, 6, and 7 occupied rooms:
P(X >= 4) = P(X = 4) + P(X = 5) + P(X = 6) + P(X = 7) = 0.339 + 0.395 + 0.266 + 0.122 = 0.923. Therefore, the probability that at least 4 out of the 7 hotel rooms are occupied on any weekend night is approximately 0.923, or 92.3% when rounded to three decimal places.
Learn more about probability here: brainly.com/question/32117953
#SPJ11
hey guys! which one is it (photo below)


Answers
Which value could be substituted for the variable to make the equation TRUE? 24 = 4y
Answers
Explanation = you have to do the inverse operation. The equation is showing:
4 times y=24. To do the inverse you do 24 divided by 4, giving the answer 6. Hope that helps :)
Cherries are $2.00/ pound what is the constant of proportionality
Answers
Answer:
$2 price per pound
2 is the constant of proportionality
Step-by-step explanation:
Price of Cherries = $2 per pound
what is the constant of proportionality
If y = total cost of buying x pounds of Cherries at $2 per pound
The equation below represent the situation
y = $2 * x
y = 2x
The constant of proportionality is 2
That is, the $2 price per pound
What is the x-coordinate of the point shown in the graph?
2
08
X
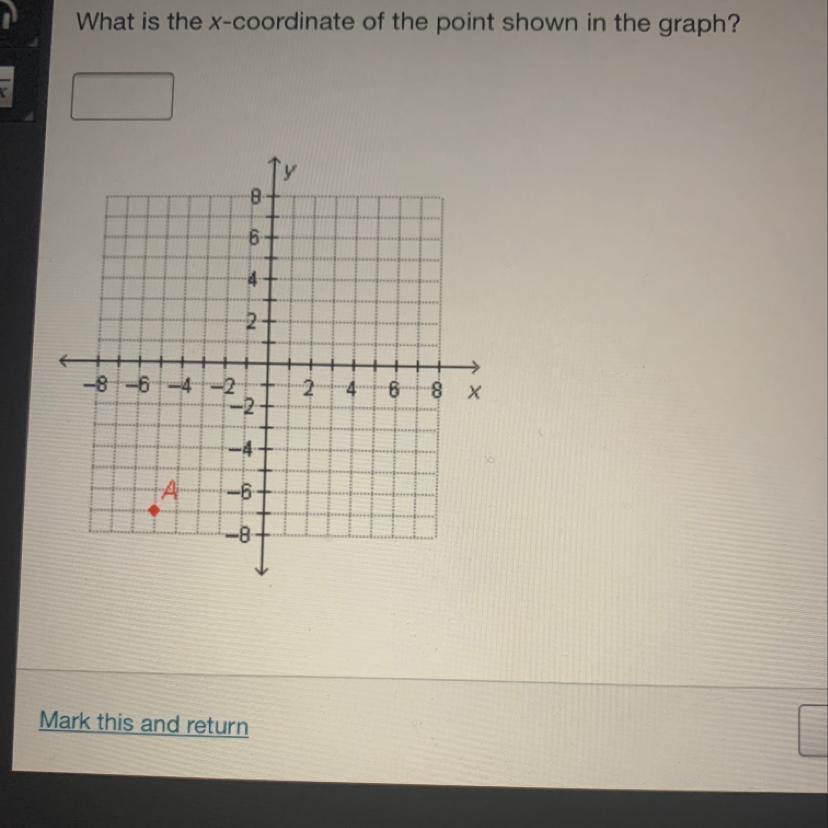
Answers
Answer:
-5
Step-by-step explanation:
The point A is located at (-5, -7), as shown in the graph. The x-coordinate is -5, and the y-coordinate is -7.
Answer:
X coordinate is -5
Step-by-step explanation:
Since, the value of x- axis at a time is 2 to the right and -2 to the left,the point between -4 and -6 can be noted as -5.
Then,y coordinate is also -7, since y axis also follows the same as x axis where one unit of x as well as y is 2.
Find the volume of a sphere whose radius is 13 feet. Round your answer to two decimal places. (use = 3.14)
Answers
Answer:
9,202.77
Step-by-step explanation:
This is off of g/o/o/g//l/e/// btw hope this helped
5. [5 marks] Using the definition of the derivative, determine f^{\prime}(x) given f(x)=2 x^{2}-x+3 .
Answers
the definition of the derivative, determine of f(x) = 2x^2 - x + 3 is f'(x) = 4x - 1.
To find the derivative using the definition, we apply the limit definition of the derivative:
f'(x) = lim(h->0) [(f(x+h) - f(x))/h]
Substituting f(x) = 2x^2 - x + 3 into the equation, we have:
f'(x) = lim(h->0) [((2(x+h)^2 - (x+h) + 3) - (2x^2 - x + 3))/h]
Expanding and simplifying the expression, we get:
f'(x) = lim(h->0) [(4xh + 2h^2 - h)/h]
Canceling out the h term, we obtain:
f'(x) = lim(h->0) (4x + 2h - 1)
Taking the limit as h approaches 0, the h term disappears, and we are left with:
f'(x) = 4x - 1
Therefore, the derivative of f(x) = 2x^2 - x + 3 is f'(x) = 4x - 1.
Learn more about derivative here:
https://brainly.com/question/29020856
#SPJ11
WILL MARK BRAINLIEST IF CORRECT

Answers
Answer:
it is actually 70
Step-by-step explanation:
Answer:
72
Step-by-step explanation:
x + ( x + 2 ) + ( x + 4 ) = 210
3x + 6 = 210
3x = 204
x = 68
Remember that x is the smallest, so we have to add 4 to 68 to get the largest of the 3 consecutive even integers: 68 + 4 = 72.
A trail mix recipe asks for 4 cups of raisins for every 6 cups of peanuts. There is a proportional relationship between the number of raisins, r (cups), and the number of peanuts, p (cups), in this recipe.
Answers
The proportion relationship between the number of raisins, r (cups), and the number of peanuts, p (cups), in the recipe is: r:p = 4:6
This can also be written as: r/p = 4/6 = 2/3. This means that for every 2 cups of raisins used in the recipe, there should be 3 cups of peanuts used. A proportional relationship is a relationship between two quantities in which they change in size in a consistent and predictable way. This means that when one quantity is multiplied or divided by a certain factor, the other quantity is also multiplied or divided by the same factor. In other words, the ratio between the two quantities remains constant, even as the individual quantities themselves may change. Proportional relationships are commonly used but in mathematics, science, and everyday life to compare and analyze quantities that are related to each other.
To learn more about proportion relationship here:
https://brainly.com/question/29765554
#SPJ1
what is the smallest three digist number divisible by the first three prime numbeers and the first three composite numberse
Answers
The smallest three-digit number divisible by the first three prime numbers (2, 3, and 5) and the first three composite numbers (4, 6, and 8) is 120.
The first three prime numbers are 2, 3, and 5. The first three composite numbers are 4, 6, and 8. In order for a number to be divisible by all six of these numbers, it must be divisible by their least common multiple (LCM).
The LCM of 2, 3, 5, 4, 6, and 8 is 120. Therefore, the smallest three-digit number divisible by the first three prime numbers and the first three composite numbers is 120.
Here is a more detailed explanation of how to calculate the LCM:
Find the prime factorization of each number.
Find the highest power of each prime factor.
Multiply the prime factors together, using the highest power for each factor.
The prime factorization of 2 is 2^1.The prime factorization of 3 is 3^1.The prime factorization of 5 is 5^1.The prime factorization of 4 is 2^2.The prime factorization of 6 is 2^1 * 3^1.The prime factorization of 8 is 2^3.The highest power of 2 that appears in any of the prime factorizations is 2^3.
The highest power of 3 that appears in any of the prime factorizations is 3^1.
The highest power of 5 that appears in any of the prime factorizations is 5^1.
Therefore, the LCM of 2, 3, 5, 4, 6, and 8 is 2^3 * 3^1 * 5^1 = 120.
To know more about number click here
brainly.com/question/28210925
#SPJ11
The function g is continuous on the interval [a, b] and is differentiable on (a, b). Suppose that g(x) = 0 for 4 distinct values of x in (a, b). What is the minimum number, k, of z in (a, b) such that g'(z) = 0?
Answers
We have to find the minimum number, k, of z in (a, b) such that g'(z) = 0. The function g is continuous on the interval [a, b] and is differentiable on (a, b). Suppose that g(x) = 0 for 4 distinct values of x in (a, b).
Let x1, x2, x3, and x4 be the four distinct values of x such that g(x) = 0.Now consider the following cases:Case 1: All four x1, x2, x3, x4 are local extrema of g(x).If this is the case, then g′(x1)=g′(x2)=g′(x3)=g′(x4)=0. Therefore, the minimum number, k, of z in (a, b) such that g′(z) = 0 is 4.Case 2:
There are less than four local extrema of g(x).In this case, by Rolle's Theorem, there exists at least one point z in (a, b) such that g′(z)=0. Since there are less than four local extrema of g(x), this point z is not equal to any of x1, x2, x3, and x4. Therefore, the minimum number, k, of z in (a, b) such that g′(z) = 0 is 1.In conclusion, the minimum number, k, of z in (a, b) such that g′(z) = 0 is either 1 or 4 depending on whether there are less than four local extrema of g(x) or all four x1, x2, x3, and x4 are local extrema of g(x).
Learn more about distinct values:
https://brainly.com/question/30042754
#SPJ11
PIz HeIp The circumference of the red circle is approximately ____ units. Use 3.14 for π.
Do not round your answer.

Answers
The circumference of the circle inscribed in a square of side 14 units is 43.96 units, on the basis of the fact that the diameter of the circle will be equal to the side of the square.
What is circumference?
Circumference is the length of a circle's boundary or the perimeter of any circular object or figure.A circle's circumference or an elliptical two-dimensional figure's perimeter are the same. Either the radius or the diameter of the circle are necessary components to calculate the circumference.
Circumference of circle=2πr {where r=radius}
=πd {where d=diameter}
Given that the circle is inscribed in the square & it is the maximum possible circle that would fit inside the square of 14 units.
The diameter of circle= side of square that inscribes circle
d = 14 units
Circumference of circle=πd
=π(14)
=14π {in terms of π}
Circumference of circle=14π
=14(3.14) {taking π=3,14}
=43.96 units
Circumference of circle=43.96 units
To know more about circumference, visit:
https://brainly.com/question/28757341
#SPJ1
How do you solve unknown angle problems in algebra?
Answers
To find any unknown angle in algebra we use the different properties of the angles.
Some of the properties of angle include alternate interior angle, corresponding angles, exterior angle as well as sum of the angles. Suppose we have a quadrilateral having three angles as 75°, 85° and 95° and we need to find the unknown angle. We know that the sum of all the interior angles of quadrilateral is equal to 360°. So we assume that the unknown angle is x°. By using the property we write the algebraic expression as
x° + 75° + 85° + 95° = 360°
x° + 255° = 360°
x° = 360° - 255°
x° = 105°
Thus the unknown angle is determined by using geometry as well as algebra.
Learn more about Quadrilateral at:
brainly.com/question/23935806
#SPJ4
What is the height, h, of the rectangular prism shown below?
Round your answer to the nearest tenth.
Answers
The height (h) of this rectangular prism is equal to 3 units.
What is Pythagorean theorem?Pythagorean theorem can be defined as a mathematical expression in Euclidean geometry that can be used to solve for any of the three (3) side lengths of a right triangle.
How to determine the height (h) of this rectangular prism?In order to determine the height (h) of this rectangular prism, we would first of all determine the diagonal of the base by applying Pythagorean theorem:
d² = l² + b²
d² = 4² + 3²
d² = 16 + 9
d² = 25
d = √25
d = 5 units.
Therefore, the diagonal of the base of this rectangular prism is equal to 5 units.
Now, we can determine the height (h) of this rectangular prism:
x² = d² + h²
h² = √34² - 5²
h² = 34 - 25
h² = 9
h = √9
Height, h = 3 units.
Therefore, the height (h) of this rectangular prism is equal to 3 units.
Read more on height of a rectangular prism here: https://brainly.com/question/13019376
#SPJ1

jada walks at a speed of 3mph. elena walks at a speed of 2.8 mph. if they both begin walkign along a walking trail at the same time, how much father will jada walk adter 3 hours
Answers
Given, Jada walks at a speed of 3 mph and Elena walks at a speed of 2.8 mph.Both Jada and Elena start walking along a walking trail at the same time.
Let us determine the distance covered by both of them.Distance travelled by Jada in 3 hours is:Distance = Speed × Time= 3 mph × 3 hours= 9 miles Distance travelled by Elena in 3 hours is:Distance = Speed × Time= 2.8 mph × 3 hours= 8.4 miles Thus, Jada will walk 0.6 miles farther than Elena after 3 hours.
To determine how far Jada will walk after 3 hours, we need to calculate the distance traveled based on her speed.
Jada walks at a speed of 3 miles per hour (mph), so we can calculate her distance using the formula:
Distance = Speed × Time
Plugging in the values, we have:
Distance = 3 mph × 3 hours
Distance = 9 miles
Therefore, Jada will walk a distance of 9 miles after 3 hours.
To know more about speed, visit:
https://brainly.com/question/13943409
#SPJ11
The given information is as follows:
Jada walks at a speed of 3 mph and Elena walks at a speed of 2.8 mph. If they both begin walking along a walking trail at the same time.
Therefore, Jada will walk 9 miles after 3 hours.
The distance covered by Jada after 3 hours can be calculated as follows:
Distance = Speed x Time
Since Jada walks at a speed of 3 mph, the distance covered by her in 3 hours can be calculated as:
Distance covered by Jada = 3 mph x 3 hours
= 9 miles.
Therefore, Jada will walk 9 miles after 3 hours.
To know more about distance visit
https://brainly.com/question/3705327
#SPJ11
Anaiah is currently consuming 20 eggplants and 30 kiwis. his marginal utility per dollar spent on the 20th eggplant is 160 utils and his marginal utility per dollar spent on the 30th kiwi is 190 utils. the price of an eggplant is $3 and the price of a kiwi is also $3. he has $180 to spend.How much is Anaiah currently spending on these goods?What are the reasons that Anaiah is behaving irrationaly?- he is not spending his entire income- he is spending to much on kiwis- he is not balancing what he spends.on each good- his marginal utility per dollar spent is not the same for both goods
Answers
a) Anaiah currently spending $150 on these goods
b) His behavior is irrational because,
option (1) He is not spending his entire income, option (2) He is spending too much on kiwis and option (3) He is not balancing his spending on each good to achieve maximum total utility.
Based on the given information, Anaiah is currently spending $150 on these goods, which is calculated by adding the total cost of eggplants and kiwis as follows:
Cost of 20 eggplants = 20 x $3 = $60
Cost of 30 kiwis = 30 x $3 = $90
Total cost = $60 + $90 = $150
Anaiah is behaving irrationally because he is not spending his entire income of $180, which means he is not maximizing his utility. Additionally, he is spending too much on kiwis, as indicated by the higher marginal utility per dollar spent on the 30th kiwi compared to the 20th eggplant.
This suggests that he would derive more satisfaction from spending more on eggplants and less on kiwis. Lastly, his marginal utility per dollar spent is not the same for both goods, which implies that he is not balancing his spending on each good to achieve the maximum total utility. Therefore, Anaiah could improve his spending behavior by adjusting his purchases to reflect a better balance of marginal utility per dollar spent on each good.
Therefore, the correct options are option (1) He is not spending his entire income, option (2) He is spending too much on kiwis and option (3) He is not balancing his spending on each good to achieve maximum total utility.
Learn more about marginal utility here
brainly.com/question/15561406
#SPJ4
tommy wait, a minor league baseball pitcher, is notorious for taking an excessive amount of time between pitches. in fact, his times between pitches are normally distributed with a mean of 36 seconds and a standard deviation of 2.5 seconds. what percentage of his times between pitches are a. longer than 39 seconds? b. between 29 and 34 seconds?
Answers
(a) 11.51 percent of tommy's times between pitches are longer than 39 seconds.
What is Normal Distribution?
We are given a Normal Distribution, which is a continuous probability distribution and is symmetrical around the mean. The shape of this distribution is like a bell curve and most of the data is clustered around the mean. The area under this bell-shaped curve represents the probability.
How to use z-table?
Step 1: In the z-table, find the two-digit number on the left side corresponding to your z-score. (e.g 0.9 1.4, 2.2, 0.5, etc.)
Step 2:Then look up at the top of the z-table to find the remaining decimal point in the range of 0.00 to 0.09. (e.g. if you are looking for 0.95 then go for the 0.05 column)
Step 3:Finally, find the corresponding probability from the z-table at the intersection of step 1 and step 2. We want to find out the probability that what percentage of his times between pitches are longer than 31 seconds.
Here, In the given question: we have,
Mean=36 seconds
Standard deviation = 2.5 seconds
So,
For x>39
We want to find out the probability that what percentage of his times between pitches are longer than 39 seconds.
\(\begin{aligned}&P(X > 39)=1-P(X < 39) \\&P(X > 39)=1-P\left(Z < \frac{x-\mu}{F}\right) \\&P(X > 39)=1-P\left(Z < \frac{39-36}{2.5}\right) \\&P(X > 31)=1-P\left(Z < \frac{3}{2.5}\right) \\&P(X > 39)=1-P(Z < 1.2)\end{aligned}\)
The z-score corresponding to 1.2 is 0.8849
\(\begin{aligned}&P(X > 39)=1-0.8849 \\&P(X > 39)=0.1151 \\&P(X > 39)=11.51 \%\end{aligned}\)
Therefore, 11.51% of his times between pitches are longer than 39 seconds.
To learn more about Normal distribution visit:
https://brainly.com/question/4079902
#SPJ4
George performs an experiment where he flips a coin 2 times. If he performs this experiment 100 times, what is the best prediction for the number of repetitions of the experiment that will result in both the two filps landing on heads?
Answers
Answer:
The probability of getting heads on a single coin flip is 1/2. The probability of getting heads on two coin flips in a row is (1/2) * (1/2) = 1/4. Therefore, if George performs this experiment 100 times, we can expect that he will get both flips landing on heads about 25 times
Step-by-step explanation:
help pleaseee i can’t get it right

Answers
The compositions between functions f(x) = 3 · x - 2 and g(x) = x + 1 are f[g(x)] = 3 · x + 1 and g[f(x)] = 3 · x - 1, respectively.
How to use composition between two functions
Let be f(x) and g(x) functions, there is a composition of the form f[g(x)], when the independent variable of function f is substituted by function g. That is to say:
f ° g(x) = f [g(x)]
First, define functions f(x) and g(x):
f(x) = 3 · x - 2
g(x) = x + 1
Second, perform the required compositions and simplify the expressions:
f[g(x)] = 3 · (x + 1) - 2
f[g(x)] = 3 · x + 1
g[f(x)] = (3 · x - 2) + 1
g[f(x)] = 3 · x - 1
To learn more on composition of functions: https://brainly.com/question/14626983
#SPJ1
A company makes chocolate candies in the shape of a solid sphere. Each piece of candy has a diameter of 3. If a box contains 30 pieces of candy, how much chocolate does the box contain? use 3. 14 for , and do not round your answer
Answers
A box of 30 pieces of chocolate candies contains approximately 424.11 cubic units of chocolate.
The volume of a sphere can be calculated using the formula:
V = (4/3) * π * r^3
where V is the volume, π is pi (approximately 3.14), and r is the radius of the sphere.
Since the diameter of each candy is 3, the radius is half of that, or 1.5. We can plug this value into the formula to find the volume of one piece of candy:
V = (4/3) * π * r^3
V = (4/3) * 3.14 * 1.5^3
V ≈ 14.137
So one piece of candy has a volume of approximately 14.137 cubic units. To find the total amount of chocolate in a box of 30 candies, we can simply multiply the volume of one candy by the number of candies in the box:
Total volume = 14.137 * 30
Total volume = 424.11
Therefore, a box of 30 pieces of chocolate candies contains approximately 424.11 cubic units of chocolate.
Learn more about candies here
https://brainly.com/question/26368371
#SPJ11
Ina Crespo rowed 20 miles down the Habashabee River in 2 hours, but the return trip took her 5 hours. Find the rate Ina rows in still water and the rate of the current Let x represent the rate Ina can row in still water and let y represent the rate of the current.
Answers
The rate Ina rolled in still water is 7 miles/ hour and the rate he rolled in the current is 3 miles/hour
Word problems leading to the addition of vectorsWord problems are encountered in our daily lives and with the use of appropriate mathematical knowledge, we can approach them rightly and get the desired solution we needed.
Word problems can be interpreted by the use of variables, the coefficient of the variables, integers, and their arithmetic operations.
In this question, we will be solving word problems that require the addition of vectors. The question talks about Ina Crespo who rolled the canoe down the river in the same direction, as such we can interpret the expression as:
\((v_x + v_y) = \dfrac{d}{2}\)
When he rolled up, i.e. in the reverse direction(negative direction), we have:
\((v_x -v_y) = \dfrac{d}{5}\)
Now, adding the two equations together, we have:
\(2v_x = \dfrac{d}{2}+\dfrac{d}{5}\)
\(2v_x = \dfrac{20}{2}+\dfrac{20}{5}\)
\(v_x = 7\)
Replacing the value of v_x into \((v_x + v_y) = \dfrac{d}{2}\)
\((7+ v_y) = \dfrac{20}{2}\)
\(v_y = 3\)
Therefore, we can conclude that the rate Ina rolled in still water is 7 miles/ hour and the rate he rolled in the current is 3 miles/hour.
Learn more about solving word problems leading to the addition of vectors here:
https://brainly.com/question/13715716
#SPJ1
for a standard normal distribution, what is the probability that z is greater than 1.75? a) 0.0401 b) 0.0459 c) 0.4599 d) 0.9599
Answers
For the standard normal distribution , the probability will be 0.0401 which means option a is the correct choice.
A standard deviation (or σ) is a degree of ways dispersed the records is when it comes to the mean. Low general deviation approach records are clustered across the mean, and excessive general deviation suggests records are extra unfold out.
Using a standard normal table the area to the right of z = 1.75 is given by
P(z > 1.75) = .0401
Therefore, the correct option is a.
To learn more about probability check the link below:
https://brainly.com/question/13604758
#SPJ4
Y=x-10 Y=-4x-5
Solve using substitution
Answers
Answer:
x = 1
Step-by-step explanation:
Both equations can be set equal to each other since they are both equal to y:
\(x-10=-4x-5\\5x-10=-5\\5x=5\\x=1\)
equate both equations !
x - 10 = -4x - 5
5x - 10 = -5
5x = 5
x = 1
therefore x = 1
find the distance between the points (4,22) and (20,10)
Answers
Answer: (16,-12)
Step-by-step explanation: just cuz... just listen linda
Answer:
(16,-12)
Step-by-step explanation:
I used a graph to get this answer
The height, h in feet, of a tree is a function of the time, t in years since it was planted. a) what is the input quantity? ___________________ output quantity? ________________ input variable? ________ output variable? ________ b) ordered pairs are represented as: ( ___ , ___ ) c) use function notation to illustrate the relationship between h and t. ________________ d) interpret h(20) = 60
Answers
Input quantity: Time t in years since it was planted
Output quantity: Height h in feet of the tree.
Input variable: time t
Output variable: height h.
Ordered pairs are represented as (t, h).
Use function notation to illustrate the relationship between h and t.
h = f(t) where f is a function of time t.
The notation h(20) = 60 means that when the tree is 20 years old, its height is 60 feet. It means that after 20 years of planting the tree, its height is 60 feet.
The input quantity is time, the output quantity is height, the input variable is t, and the output variable is h. The relationship between height and time can be expressed as a function h = f(t).
Finally, the function notation h(20) = 60 means that the tree's height is 60 feet after 20 years.
To know more about Ordered pairs visit :
brainly.com/question/28874341
#SPJ11
Select the expression which does not simplify to y³

Answers
Answer:
d) y^6/y^2
Step-by-step explanation:
y^6/y^2= y^4
Answer:
Last Option \( {y}^{6} \div {y}^{2} \)Step-by-step explanation:
This is because,
As,
\( {a}^{x} \div {a}^{y} = {a}^{x - y} \)
Here ,
\( {y}^{6} \div {y}^{2} \)
\( = {y}^{6 - 2} \)
\( = {y}^{4} \)
And here the result does not simplify to,
\( {y}^{3} \)
Hence, Last Option is the correct answer
Find each sum or difference
1. (4a - 5)+(3a + 6)
2. (6x + 9)+ (4x^2 - 7)
3. (6xy + 2y + 6x) + (4xy - x)
Answers
1. (4a - 5)+(3a + 6) = 7a + 1.
To solve, you simply combine the like terms (4a and 3a) to get 7a, and then combine the constants (-5 and 6) to get 1.
2. (6x + 9)+ (4x^2 - 7) = 4x^2 + 6x + 2.
To solve, you combine the like terms (6x and 4x^2) to get 4x^2 + 6x, and then combine the constants (9 and -7) to get 2.
3. (6xy + 2y + 6x) + (4xy - x) = 10xy + 2y + 6x - x = 10xy + 2y + 5x.
To solve, you combine the like terms (6xy and 4xy) to get 10xy, then combine the constants (2y and -x) to get 2y - x, and finally combine the like terms (6x and 5x) to get 11x. The final answer is 10xy + 2y + 5x.
Know more about constants here:
https://brainly.com/question/27983400
#SPJ11
Find the fixed points of the function f(x, y) = (x2, xy). [2 marks] (c) Equip R2 with the taxi metric: dı((x, y), (u', y')) = (x – X'| + \y – y'l. For what values of c E R is the function f from the previous part a strict contraction on the region 2 1 1 [?] Х CR2? (5 marks) (d) Which of the following metric spaces are compact? (i) [3, 17] ×[-5, 12] CR2, equipped with the Euclidean metric. (ii) A finite set X, equipped with the discrete metric. (iii) The metric space ll. You do not need to justify your answers. [3 marks
Answers
a) The fixed points of the function are (0, 0) and (1, 1).
b) The given function f(x, y) = (x², xy) is a strict contraction on the region { (x, y) : 0 ≤ x, y ≤ 1} equipped with the taxi metric for any c > 4.
c) (i) The Euclidean metric-equipped metric space [3, 17] [-5, 12] is compact.
(ii) A discrete metric equipped finite set X is compact.
(iii)The metric space l2 isn't compact.
d) The compact metric spaces are: (i) [3, 17] ×[-5, 12] CR2, equipped with the Euclidean metric(ii) A finite set X, equipped with the discrete metric.(iii) The metric space ll.
a) Finding fixed points of the function f(x,y) = (x²,xy)
The given function is f(x, y) = (x², xy). To find the fixed points of the function, we need to solve the following system of equations:x = x²y = xy => y = 1 or x = 0 or both
b) Values of c for which f is a strict contraction
We have the function f(x, y) = (x², xy) and the metric space R² equipped with the taxi metric: d((x, y), (u', y')) = |x – u'| + |y – y'|.A function f: (X, d) → (X, d) is a strict contraction on the metric space (X, d) if there exists some k ∈ [0, 1) such that d(f(x), f(y)) ≤ k d(x, y), for all x, y ∈ X.
c) Compactness of given metric spaces
(i) The metric space [3, 17] × [-5, 12] equipped with the Euclidean metric is compact.
(ii) A finite set X equipped with the discrete metric is compact.
(iii) The metric space l² is not compact.
(d) The discrete metric space is compact, because any open covering of the discrete metric space has a finite subcover. The other two metric spaces are not compact. In the Euclidean metric space, [3, 17] ×[-5, 12], the sequence (x_n) = (3 + 1/n, 0) has no convergent subsequence. In the metric space l∞, the sequence (x_n) = (1, 1/2, 1/3, ...) has no convergent subsequence.
To know more about metric space click on below link:
https://brainly.com/question/32540508#
#SPJ11
Which of the following represents the sum of
(x2 - 7x + 6) + (x2 + 6x)
Ox? - x + 6
2x2 - 7x + 12
1 2x² - x + 6
x2 - 7x + 12
Answers
Answer:
Solution given:
(x²-7x+6)+(x²+6x)
open bracket
x²-7x+6+x²+6x
keep like terms together
x²+x²-7x+6x+6
solve like terms
2x²-x+6
option 3rd
2x² - x + 6
\\ thank \: you\)
I hope this helps you
