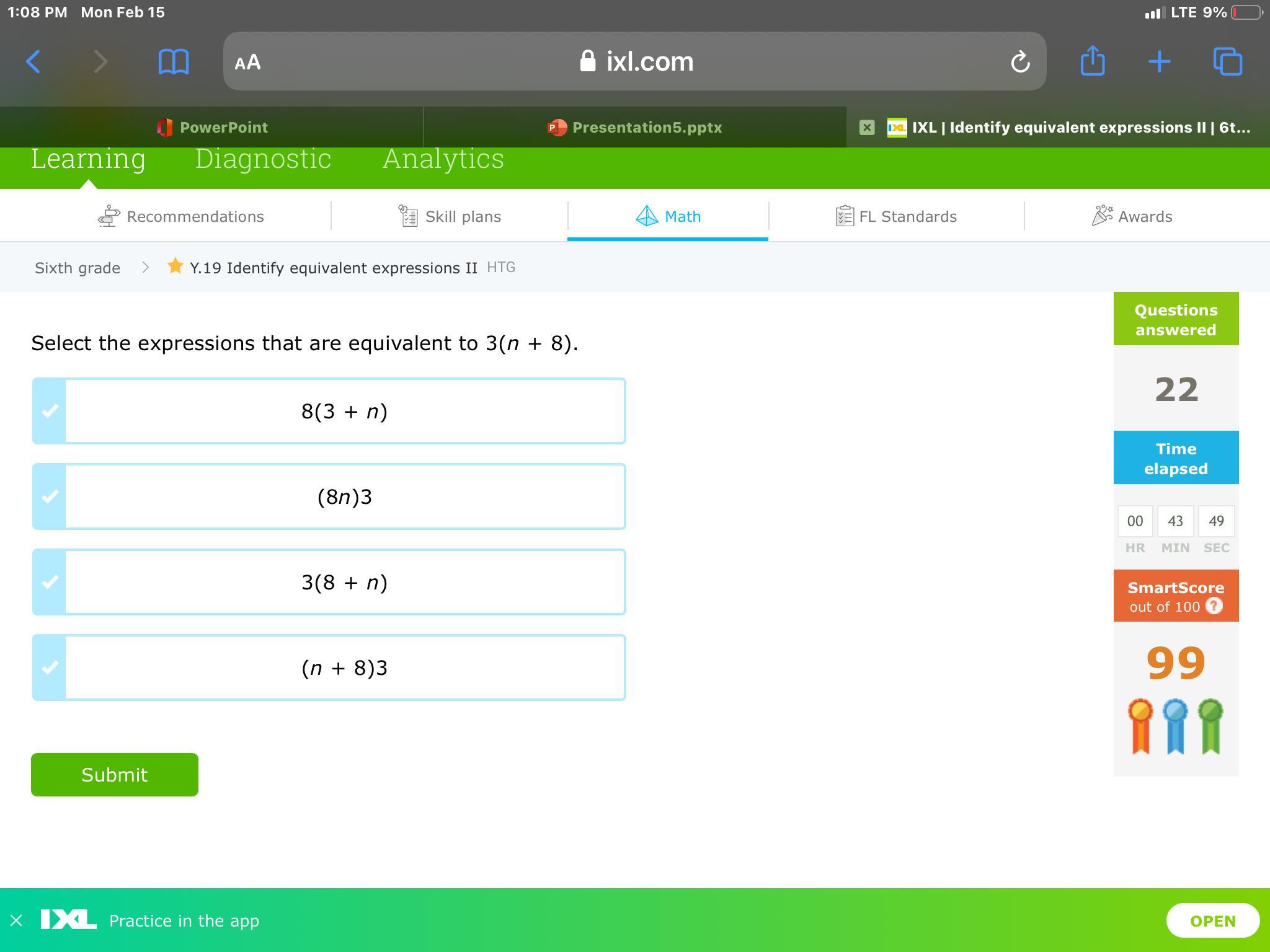
Answers
Answer:
D
Step-by-step explanation:
it does not matter which side you put the eight.
Related Questions
We would like to construct a 99% confidence interval for the mean, based on a sample of 50 observations. The sample standard deviation is 5.5 and the sample mean is 22. The population standard deviation is 3.6. Calculate the lower confidence limit. Round your answer to 3 decimals if needed
Answers
Answer:
Lower confidence limit = 20.191
Step-by-step explanation:
Sample mean; x' = 22
Sample standard deviation; s = 5.5
Sample size; n = 50
Confidence interval = 99%
Since sample size > 30, we will use the formula;
CI = x' ± zs/√n
Where;
x' is sample mean
s is sample standard deviation
n is sample size
z is z-value of the confidence interval
From the table attached, z for 99% = 2.3263
Thus;
CI = 22 ± (2.3263 × 5.5)/√50
CI = 22 ± 1.809
CI = 23.809 or 20.191
Lower confidence limit = 20.191

Caculate.
2 1/4÷(3/8÷1/2)
Answers
let's firstly convert the mixed fraction to improper fraction and proceed from there.
\(\stackrel{mixed}{2\frac{1}{4}}\implies \cfrac{2\cdot 4+1}{4}\implies \stackrel{improper}{\cfrac{9}{4}} \\\\[-0.35em] ~\dotfill\\\\ \cfrac{9}{4}\div \left(\cfrac{3}{8}\div \cfrac{1}{2} \right)\implies \cfrac{9}{4}\div \left(\cfrac{3}{8}\cdot \cfrac{2}{1} \right)\implies \cfrac{9}{4}\div \left(\cfrac{3}{4} \right) \\\\\\ \cfrac{9}{4}\cdot \left(\cfrac{4}{3} \right)\implies \cfrac{9}{3}\cdot \cfrac{4}{4}\implies 3\cdot 1\implies \text{\LARGE 3}\)
A triangular prism has a base of 6cm, 8cm, and 10cm long. Its lateral area is 744cm?.What is the height of the solid?
Answers
We have the following equation for the lateral surface area of a triangular prism:
\(A=h(a+b+c)\)where a,b and c are the measures of the sides of the triangular base.
In this case, we have the following:
\(\begin{gathered} A=744 \\ a=6 \\ b=8 \\ c=10 \end{gathered}\)using the formula, we get:
\(744=h(6+8+10)\)now, we can solve for h to find the height:
\(\begin{gathered} h(6+8+10)=744 \\ \Rightarrow24h=744 \\ \Rightarrow h=\frac{744}{24}=31 \\ h=31 \end{gathered}\)therefore, the height of the solid is 31 cm
Which of the following measurements must be accurate when used at a grocery store?
Answers
Answer:
Package
Step-by-step explanation: Hope it helps.
Solve the exponential equation: 3- x = 1
OA) X=0
x
OB) x= 1
OC) x=-2
x=
OD) x= 2

Answers
\(~\hspace{7em}\textit{negative exponents} \\\\ a^{-n} \implies \cfrac{1}{a^n} ~\hspace{4.5em} a^n\implies \cfrac{1}{a^{-n}} ~\hspace{4.5em} \cfrac{a^n}{a^m}\implies a^na^{-m}\implies a^{n-m} \\\\[-0.35em] \rule{34em}{0.25pt}\\\\ 3^{2-x}=1\implies 3^2\cdot 3^{-x}=1\implies 3^2\cdot \cfrac{1}{3^x}=1\implies \cfrac{3^2}{3^x}=1 \\\\\\ 3^2=3^x\implies 2=x\)
Draw the base plan for the set of stacked cubes. Assume that no cubes are hidden form view.

Answers
Answer:
Given Figure has set of Stacked cubes.
To Draw the Base Plan, lets see its right side, Left Side and Front side view.
Right side:
It has 3 cubes in base.
2 cubes in 2nd layer clearly seen in figure and only 1 cube in 3rd layer.
Left Side:
It has 2 Cubes in base.
Both Cubes attached to 1st and 2nd cube of right side cubes.
Front Side:
It can be seen that, here base only has 2 rows of cubes.
Therefore, 1st Figure is correct Base Plan (or enclosed figure)
Note: Numbers in enclosed figure just shows the total no. of cubes in that stack.
To know more about base plan check:
https://brainly.com/question/29579988
#SPJ1

Consider a medium with parameters € = 1.2 (10^-10 )F/m , n= 3(10^-3) H/m and sigma=0. Magnetic field intensity in the medium is given as R = 2cos (10^10t- 600x)äz Am.
Use Maxwell's equations to obtain the followings:
1) Magnetic flux density
These questions is circuit theory
Answers
Using Maxwell's equations, we can determine the magnetic flux density. One of the Maxwell's equations is:
\(\displaystyle \nabla \times \mathbf{H} = \mathbf{J} + \frac{\partial \mathbf{D}}{\partial t}\),
where \(\displaystyle \nabla \times \mathbf{H}\) is the curl of the magnetic field intensity \(\displaystyle \mathbf{H}\), \(\displaystyle \mathbf{J}\) is the current density, and \(\displaystyle \frac{\partial \mathbf{D}}{\partial t}\) is the time derivative of the electric displacement \(\displaystyle \mathbf{D}\).
In this problem, there is no current density (\(\displaystyle \mathbf{J} =0\)) and no time-varying electric displacement (\(\displaystyle \frac{\partial \mathbf{D}}{\partial t} =0\)). Therefore, the equation simplifies to:
\(\displaystyle \nabla \times \mathbf{H} =0\).
Taking the curl of the given magnetic field intensity \(\displaystyle \mathbf{R} =2\cos( 10^{10} t-600x)\hat{a}_{z}\, \text{Am}\):
\(\displaystyle \nabla \times \mathbf{R} =\nabla \times ( 2\cos( 10^{10} t-600x)\hat{a}_{z}) \, \text{Am}\).
Using the curl identity and applying the chain rule, we can expand the expression:
\(\displaystyle \nabla \times \mathbf{R} =\left( \frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial y} -\frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial z}\right) \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Since the magnetic field intensity \(\displaystyle \mathbf{R}\) is not dependent on \(\displaystyle y\) or \(\displaystyle z\), the partial derivatives with respect to \(\displaystyle y\) and \(\displaystyle z\) are zero. Therefore, the expression further simplifies to:
\(\displaystyle \nabla \times \mathbf{R} =-\frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial x} \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Differentiating the cosine function with respect to \(\displaystyle x\):
\(\displaystyle \nabla \times \mathbf{R} =-2( 10^{10}) \sin( 10^{10} t-600x)\hat{a}_{z} \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Setting this expression equal to zero according to \(\displaystyle \nabla \times \mathbf{H} =0\):
\(\displaystyle -2( 10^{10}) \sin( 10^{10} t-600x)\hat{a}_{z} \mathrm{d} x\mathrm{d} y\mathrm{d} z =0\).
Since the equation should hold for any arbitrary values of \(\displaystyle \mathrm{d} x\), \(\displaystyle \mathrm{d} y\), and \(\displaystyle \mathrm{d} z\), we can equate the coefficient of each term to zero:
\(\displaystyle -2( 10^{10}) \sin( 10^{10} t-600x) =0\).
Simplifying the equation:
\(\displaystyle \sin( 10^{10} t-600x) =0\).
The sine function is equal to zero at certain values of \(\displaystyle ( 10^{10} t-600x) \):
\(\displaystyle 10^{10} t-600x =n\pi\),
where \(\displaystyle n\) is an integer. Rearranging the equation:
\(\displaystyle x =\frac{ 10^{10} t-n\pi }{600}\).
The equation provides a relationship between \(\displaystyle x\) and \(\displaystyle t\), indicating that the magnetic field intensity is constant along lines of constant \(\displaystyle x\) and \(\displaystyle t\). Therefore, the magnetic field intensity is uniform in the given medium.
Since the magnetic flux density \(\displaystyle B\) is related to the magnetic field intensity \(\displaystyle H\) through the equation \(\displaystyle B =\mu H\), where \(\displaystyle \mu\) is the permeability of the medium, we can conclude that the magnetic flux density is also uniform in the medium.
Thus, the correct expression for the magnetic flux density in the given medium is:
\(\displaystyle B =6\cos( 10^{10} t-600x)\hat{a}_{z}\).
How many decimal places are in the product?
1.684×10.2
Answers
Answer:
4
Step-by-step explanation:
in all there is 4 places behind the decimal
Answer:
4
Step-by-step explanation:
17.1768
Solve for B -(12 x 2) x (-6) = -12 x (2 x b)
A. -6
B. 6
C. -12
D. 12
Answers
Answer:
Option A
Step-by-step explanation:
-(12 x 2) x (-6) = -12 x (2 x b)
=> -24 x -6 = -12 x 2b
=> 144 = -24b
=> b = -6
Hoped this helped.
Sixteen degrees celsius is warmer than zero degrees celsius
Answers
Answer:
yes???
Step-by-step explanation:
16 celsius is warmer than 0 celsius by 16 degrees.0 is colder by 16 degrees.
T o T hope that helped...
Hello Can Someone Please Answer This I Will Mark You The Brainliest

Answers
Answer: 180 cm2
if you add up all the sides you'll get 36 in total. if you divide the answer choices by 5 (the number of sides) in ONE (180 cm2) of the answers you'll get 36.
The monthly utility bills in a city are normally distributed, with a mean of $ and a standard deviation of $. Find the probability that a randomly selected utility bill is (a) less than $, (b) between $ and $, and (c) more than $. (a) The probability that a randomly selected utility bill is less than $ is 0.0076. (Round to four decimal places as needed.) (b) The probability that a randomly selected utility bill is between $ and $ is 0.6859. (Round to four decimal places as needed.) (c) The probability that a randomly selected utility bill is more than $ is 0.0764. (Round to four decimal places as needed.)
Answers
Complete Question
The complete question is shown on the first uploaded image
Answer:
a
\(P(X < 65) = 0.003467\)
b
\(P(86 < X < 110 )= 0.63928 \)
c
\(P(X > 120 ) =0.062024\)
Step-by-step explanation:
From the question we are told that
The mean is \(\mu = \$ 100\)
The standard deviation is \(\sigma = \$ 13\)
Generally the probability that the monthly utility bills is less than $65 is mathematically represented as
\(P(X < 65) = P(\frac{X - \mu }{\sigma } < \frac{65 - 100 }{13 } )\)
Generally
\(\frac{X - \mu }{\sigma } = Z (The\ standardized \ value \ of\ X )\)
So
\(P(X < 65) = P(Z < -2.70 )\)
From the z-table
\(P(Z < -2.70 ) = 0.003467\)
So
\(P(X < 65) = 0.003467\)
Generally the probability that a randomly selected utility bill is between $86 and $110 is mathematically represented as
\(P(86 < X< 110 )= P( \frac{86 -100}{ 13} < \frac{X - \mu}{\sigma } < \frac{86 -100}{ 13} )\)
=> \(P(86 < X < 110 )= P( \frac{86 -100}{ 13} < Z < \frac{110 -100}{ 13} )\)
=> \(P(86 < X < 110 )= P(-1.08 < Z < 0.77 )\)
=> \(P(86 < X < 110 )= P(Z < 0.77 ) - P(Z < -1.08 ) \)
From the z-table
\(P(Z < 0.77 ) = 0.77935\)
and
\(P(Z < -1.08 ) = 0.14007\)
So
\(P(86 < X < 110 )= 0.77935 - 0.14007 \)
=> \(P(86 < X < 110 )= 0.63928 \)
Generally the probability that the monthly utility bills is more than $120 is mathematically represented as
\(P(X >120 ) = P(\frac{X - \mu }{\sigma } > \frac{120 - 100 }{13 })\)
=> \(P(X > 120 ) = P(Z > 1.538 )\)
From the z-table
\(P(Z > 1.54 ) = 0.062024\)
So
\(P(X > 120 ) =0.062024\)

PLS HELP! weights (in pounds) of catfish caught in the river: 4.8 3 2.7 4.4 4.8 9.9 What is the outlier? A) 3 lbs B) 4.8 lbs C) 9.9 lbs D) none
Answers
The correct answer is C) 9.9 lbs as it is above the upper boundary 6.4865, it is the outlier in this dataset.
What is an outlier?An outlier is an observation that is much higher or lower than the other observations in a dataset.
In this case, the weights of the catfish range from 2.7 to 4.8 lbs, with one observation that is much higher at 9.9 lbs.
Therefore, 9.9 lbs is the outlier in this dataset.
To find the outlier in this dataset, we can calculate the interquartile range (IQR).
This is done by first calculating the first quartile (Q1) and third quartile (Q3).
The Q1 for this dataset =3.75
and the Q3= 4.675.
IQR= Q3 - Q1
= 0.925.
We then calculate the lower boundary as Q1 - (1.5 x IQR) = 2.3625.
The upper boundary is Q3 + (1.5 x IQR)= 6.4865.
Since 9.9 lbs is above this upper boundary, it is the outlier in this dataset.
For more questions related to upper boundary
https://brainly.com/question/28725724
#SPJ1
snow is falling in syracuse, NY after 2 hours, 4 inches of snow has fallen.
1 if it continues to snow at the same rate, how many inches of snow would you expect after 6.5 hours?
2 write and equation that gives us that amount of snow that has fallen after z hours at this rate.
3 how many inches will fall in 24 hours if it continues to snow at this rate.
time (hours) snow (inches)
blank. 1
1. blank
2. 4
6.5. blank
x. blank
Answers
Answer:
1) 13 inches
2) 2z=x
3) 48 inches
Step-by-step explanation:
it snows 4/2 = 2 inches perhour
1. 2x 6.5 = 13 inches
2. y = 2z
3. 2x 24 = 48 inches
I need help with this

Answers
Answer: B
Step-by-step explanation: You can subtract 21 from 245 11 times but some will remain
Suppose that the readings on the thermometers are normally distributed with a mean of 0∘ and a standard deviation of 1.00∘C.
If 12% of the thermometers are rejected because they have readings that are too high, but all other thermometers are acceptable, find the reading that separates the rejected thermometers from the others.
Answers
The reading that separates the rejected thermometers from the others is given as follows:
1.175 ºC.
How to obtain probabilities using the normal distribution?The z-score of a measure X of a normally distributed variable that has mean represented by \(\mu\) and standard deviation represented by \(\sigma\) is obtained by the equation presented as follows:
\(Z = \frac{X - \mu}{\sigma}\)
The z-score represents how many standard deviations the measure X is above or below the mean of the distribution of the data-set, depending if the obtained z-score is positive(above the mean) or negative(below the mean).The z-score table is used to obtain the p-value of the z-score, and it represents the percentile of the measure X in the distribution.The mean and the standard deviation for this problem are given as follows:
\(\mu = 0, \sigma = 1\)
The 12% higher of temperatures are rejected, hence the 88th percentile is the value of interest, which is X when Z = 1.175.
Hence:
1.175 = X/1
X = 1.175 ºC.
More can be learned about the normal distribution at https://brainly.com/question/25800303
#SPJ1
Julia has 9 one pound bags of sand each a different color. For a art project she will use 1/8 lb of each bag of sand to create sand art jar. How much sand will be in the jar?
a. 8/9, b. 1/72, c. 1 1/9, d. 1 1/8
Answers
In what quadrant is the point (5, −8) located?
A) I
B) II
C) III
D) IV

Answers
Answer:
c) third quadrant
Step-by-step explanation:
Answer:
4
Step-by-step explanation:
the quadrants are labeled left to right. Comment if u have any questions :)
Which number is rational?
-2.101001001
-.8974512
1.2547569
5.3333333
Answers
Answer:
D
Step-by-step explanation:
Took the test
Find the length of midsegment of the trapezoid.
MN=?

Answers
The length of midsegment of the trapezoid is MN = 66.5 units
How to find the length of midsegment of the trapezoid?
The midsegment of a trapezoid is a line segment that connects the midpoints of the legs of the trapezoid.
The midsegment of a trapezoid is parallel to each base, and its length is one-half the sum of the lengths of the bases.
In this case, length of midsegment of the trapezoid will be:
MN = 1/2 × (76 + 57)
MN = 1/2 × (133)
MN = 66.5 units
Learn more about length of midsegment of a trapezoid on:
brainly.com/question/7593624
#SPJ1
A rectangle has a perimeter of 28 feet. The width of the rectangle is two foot less than the length of the rectangle. What is the width of the rectangle?
Answers
Step-by-step explanation:
perimeter of a rectangle = 2×length + 2×width = 28 ft
width = length - 2
length = width + 2
2×(width + 2) + 2×width = 28
2×width + 4 + 2×width = 28
4×width + 4 = 28
4×width = 24
width = 6 ft
and the length is width + 2 = 6+2 = 8 ft.
Please help me with this proof.

Answers
Answer:
See below
Step-by-step explanation:
For the second step, \(\angle T\cong\angle R\) by Alternate Interior Angles. The rest of the steps appear to be correct.
A current exists whenever electric charges move. If Delta Q is the net charge that passes through a surface during a time period Delta t, then the average current during this time interval is defined as average current = Delta Q/Delta t=Q2-Q1/t2-t1. If we take the limit of this average current over smaller and smaller time intervals, we get what is called the current I at a given time t1: I=lim Delta t tends to 0 Delta Q/ Delta t =dQ/dt. Thus the current is the rate at which charge flows through a surface. The current in a wire is defined as the derivative of the charge: I(t) = Q'(t). What does Integrate I(t)dt between the limits a and b represent? It represents the change in the current I from time t = a to t = b. It represents the charge Q at time t. It represents the change in the charge Q from time t = a to t = b. It represents the current I at time t.
Answers
The integral of the current I(t) over the interval [a,b] represents the change in the charge Q from time t=a to t=b.
The current in an electrical circuit is defined as the rate at which charge is flowing through a conductor. The equation that represents the current is I(t) = dQ(t)/dt, where Q(t) is the charge at time t and dQ(t)/dt is the derivative of Q(t) with respect to time, representing the rate of change of charge.
The integral of I(t) with respect to time between the limits a and b, i.e. ∫I(t)dt between the limits a and b, represents the change in the charge from time t = a to time t = b. This is because the definite integral of a rate of change gives the total change in the quantity being measured, in this case, the charge.
So, \(\int\limits^a_b {|(t)} \, dt = Q(b) -Q(a)\), which represents the change in the charge from time t = a to time t = b.
Learn more about definite integral here:
https://brainly.com/question/3356154
#SPJ4
HELP PLSSSSS :((((((

Answers

NO LINKS!! URGENT HELP PLEASE!!!
Express the statement as an inequality
d. d is between 2 and 1
1. d < 1 < 2
2. 1 < d < 2
3. 1 < 2 < d
4. 2 ≥ d ≥ 1
5. 1 ≤ d ≤ 2
e. t is not less than 5
1. t > 5
2. t < 5
3. t = 5
4. t ≥ 5
5. t ≤ 5
f. The negative of z is not greater than 4
1. -z < 4
2. z ≤ -4
3. z ≤ 4
4. z < 4
5. -z ≤ 4
Answers
Answer:
d. 1 < d < 2
e. t ≥ 5
f. -z ≤ 4
Step-by-step explanation:
Answer:
d. 5. 1 ≤ d ≤ 2
e. 4. t ≥ 5
f. 1. -z < 4
Step-by-step explanation:
d. d is between 2 and 1
The statement "d is between 2 and 1" means that d is greater than 1 and less than 2. We can represent this using the inequality 1 < d < 2. However, the answer choices do not match this exact form of inequality. To rephrase the inequality in a way that matches the answer choices, we can use the logical "and" operator to combine two inequalities: d is greater than or equal to 1, and d is less than or equal to 2. This gives us the inequality 1 ≤ d ≤ 2, which is answer choice 5.
e. t is not less than 5
The statement "t is not less than 5" means that t is greater than or equal to 5. This can be represented using the inequality t ≥ 5, which is answer choice 4.
f. The negative of z is not greater than 4
The statement "the negative of z is not greater than 4" means that -z is less than or equal to 4. We can represent this using the inequality -z ≤ 4, which is answer choice 2. However, the question does not include an answer choice for -z < 4, which is also true based on the statement.
s the last book a person in City Upper A read a discrete random variable, continuous random variable, or not a random variable? A. It is a continuous random variable. B. It is a discrete random variable.
Answers
Answer:
Not a random variable
Step-by-step explanation:
The last book a person read in City A is not a random variable because it is not a number as there is no numerical description for the outcome of this experiment.
Thus, the last book read by someone in City A is not a random variable.
Answer:
not random
Step-by-step explanation:
if I eat 230 gumballs and there was a total of 1696 and my friend takes the rest of the 1760 gumballs. how did we get 1760 if there was 1696 and I ate 230. how many gumballs was added?
Answers
294 gumballs were added because if u subtract 230 from 1696 you get 1466 which was the number you had when you are 230 gumballs so you take 1466 and subtract it from 1760 you get the amount of gumballs that was added.
just like this other lady said 294 gumballs were added
Question 6
A square is placed within a rectangle. Find the area of the shaded region.
Select one:
O
✪
✪
O
559 ft²
640 ft²
721 ft²
604 ft²
32 ft
19A
9 ft
20 ft
Answers
The area of the shaded region is 559 ft².
How to find the area of the shaded region?In order to find the area of the shaded region, we will subtract the area of the square from the area of the rectangle. That is:
area of the shaded region = area of rectangle - area of square
area of the shaded region = (32 * 20) - (9 * 9)
area of the shaded region = 640 - 81
area of the shaded region = 559 ft²
Learn more about area on:
https://brainly.com/question/21468598
#SPJ1
Complete Question
See attached image

If 35% of a number is 98 and 80% of the same number is 224, find 45% of that number.
Answers
9514 1404 393
Answer:
126
Step-by-step explanation:
If n represents the original number, we have
(35%)n = 98
(80%)n = 224
We want to find (45%)n.
(45%)n = (80% -35%)n = (80%)n -(35%)n
(45%)n = 224 -98 = 126
45% of the number is 126.
Graph the solution to this inequality on the number line.
58z>56

Answers
The graph of the solution to the inequality 5/8z > 5/6 is attached
How to graph the solution to this inequalityFrom the question, we have the following parameters that can be used in our computation:
5/8z > 5/6
Multiply both sides of the inequality by 1/5
So, we have the following representation
1/8z > 1/6
Multiply both sides of the inequality by 8
So, we have the following representation
z > 8/6
Evaluate the quotient
This gives
z > 1.33
The above inequality means that the inequality starts from 1.33 and faces the right side
See attachment for the graph
Read more about inequality at
https://brainly.com/question/25275758
#SPJ1