There's a roughly linear relationship between the length of someone's
femur (the long leg-bone in your thigh) and their expected height.
Within a certain population, this relationship can be expressed using
the formula h = 2. 46f + 60. 6, where h represents the expected
height in centimeters and f represents the length of the femur in
centimeters. What is the meaning of the f-value when h 128?
Answers
This means that in the population represented by the formula, someone with a femur length of 27.4 centimeters would be expected to have a height of 128 centimeters
When h is 128, we can use the formula h = 2.46f + 60.6 to solve for the corresponding value of f.
128 = 2.46f + 60.6
Subtracting 60.6 from both sides:
67.4 = 2.46f
Dividing both sides by 2.46:
f ≈ 27.4
Therefore, when h is 128, the f-value (length of the femur) is approximately 27.4 centimeters. This means that in the population represented by the formula, someone with a femur length of 27.4 centimeters would be expected to have a height of 128 centimeters.
To learn more about femur go to:
https://brainly.com/question/9454759#
#SPJ11
Related Questions
1. A grocery store sells salmon for $7.84 per pound. What would be the cost of 2 2/5
pounds of salmon?
Answers
In linear equations, 18.816 is the cost of 2 2/5 pounds of salmon.
What are instances of linear equations?
Ax+By=C is the usual form for two-variable linear equations. A standard form linear equation is, for instance, 2x+3y=5. Finding both intercepts of an equation in this format is rather simple (x and y).A linear equation's graph will always be a straight line. Definition of a Linear Equation.When a linear equation is graphed, it always produces a straight line since each term in the equation has an exponent of 1.grocery store sells salmon = $7.84 per pound
the cost of 2 2/5 pounds of salmon = \(2\frac{2}{5}\) × 7.84
the cost of 2 2/5 pounds of salmon = 12/5 * 7.84
the cost of 2 2/5 pounds of salmon = 12 * 1.568
the cost of 2 2/5 pounds of salmon = 18.816
Learn more about Linear Equation.
brainly.com/question/11897796
#SPJ13
The mean values are 30, 20, and 15 min, respectively, and the standard deviations are 1, 2, and 1.2 min, respectively. What is the probability that it takes at most 1 hour of machining time to produce a randomly selected component
Answers
The probability that it takes at most 1 hour of machining time to produce a randomly selected component is approximately 0.00003 or 0.003%.
To solve this problem, we need to first calculate the total mean and standard deviation for the machining time of a single component.
The total mean machining time can be found by adding the means for each component:
30 + 20 + 15 = 65 minutes
The total standard deviation can be found using the formula:
\(\sqrt{((1^2 + 2^2 + 1.2^2)/3)} = 1.247 minutes\)
Now we need to find the probability that it takes at most 1 hour (60 minutes) to produce a randomly selected component. We can use the standard normal distribution to calculate this probability.
z-score = (60 - 65) / 1.247 = -4.01
Using a standard normal distribution table, we can find that the probability of a z-score being less than or equal to -4.01 is approximately 0.00003.
for such more question on probability
https://brainly.com/question/13604758
#SPJ11
Inverse functions linear discrete

Answers
Answer:
\(\text{g}^{-1}(x)=\boxed{\dfrac{x-13}{2}}\)
\(\left(\text{g}^{-1} \circ \text{g}\right)(-4)=\boxed{-4}\)
\(h^{-1}(9)=\boxed{-3}\)
Step-by-step explanation:
To find the inverse of function g(x) = 2x + 13, begin by replacing g(x) with y:
\(y=2x+13\)
Swap x and y:
\(x=2y+13\)
Rearrange to isolate y:
\(\begin{aligned}x&=2y+13\\\\x-13&=2y+13-13\\\\x-13&=2y\\\\2y&=x-13\\\\\dfrac{2y}{2}&=\dfrac{x-13}{2}\\\\y&=\dfrac{x-13}{2}\end{aligned}\)
Replace y with g⁻¹(x):
\(\boxed{\text{g}^{-1}(x)=\dfrac{x-13}{2}}\)
\(\hrulefill\)
As g and g⁻¹ are true inverse functions of each other, the composite function (g⁻¹ o g)(x) will always yield x. Therefore, (g⁻¹ o g)(-4) = -4.
To prove this algebraically, calculate the original function g at the input value x = -4, and then evaluate the inverse function of g at the result.
\(\begin{aligned}\left(\text{g}^{-1} \circ \text{g}\right)(-4)&=\text{g}^{-1}\left[\text{g}(-4)\right]\\\\&=\text{g}^{-1}\left[2(-4)+13\right]\\\\&=\text{g}^{-1}\left[5\right]\\\\&=\dfrac{(5)-13}{2}\\\\&=\dfrac{-8}{2}\\\\&=-4\end{aligned}\)
Hence proving that (g⁻¹ o g)(-4) = -4.
\(\hrulefill\)
The inverse of a one-to-one function is obtained by reflecting the original function across the line y = x, which swaps the input and output values of the function. Therefore, (x, y) → (y, x).
Given the one-to-one function h is defined as:
\(h=\left\{(-3,9), (1,0), (3,-7), (5,2), (9,6)\right\}\)
Then, the inverse of h is defined as:
\(h^{-1}=\left\{(9,-3),(0,1),(-7,3),(2,5),(6,9)\right\}\)
Therefore, h⁻¹(9) = -3.
In a lab, a substance was cooled by 6 degrees celsius each hour for 12 hours.
The total change in temperature was what?
Answers
Answer:
72 degrees 72° Celsius. It changed by 72 degrees.
Step-by-step explanation:
6 * 12 because it changed 6 degrees each hour for 12 hours
6 *
12
—-
72
Answer:
72 degree Celsius
Step-by-step explanation:
Since every hour the temperature is cooled by 6⁰C and the total time spent was 12 hour we can do a simple multiplication shown:
6 * 12 = 72
all you need is in the photo please don't do step by step please answer fast please helppppppleaseeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeee

Answers
Part a) x=-3, x = 0, x = 2
Part b) p(x) → ∞
Explanations:a) The given function is:
p(x) = x (x + 3)(x - 2)
The zeros of the function are gotten by setting p(x) = 0
0 = x (x + 3) (x - 2)
x = 0
x + 3 = 0, x = -3
x - 2 = 0, x = 2
The zeros of the function p(x) are -3, 0, 2
b) As x → ∞
P(x) → ∞
Find a counterexample to show that the given conjecture is false.
If n is a real number, then n³>n.
Answers
Let \(n=0\). Then \(0^3 = 0\) but 0 > 0 is a false statement.
question which system of equations models the following problem if x represents the number of angelfish yves bought and y represents the number of parrotfish he bought? yves bought 420 tropical fish for a museum display. he bought 6 times as many parrotfish as angelfish. how many of each type of fish did he buy?
Answers
Thus, 420 fish were ultimately caught, with 6x standing in for "6 times as much."
Calculation:x + y = 420; y = 6x
Thus, 420 fish were ultimately caught, with 6x standing in for "6 times as much."
How well-versed are you in fish size?The smallest and largest fish range in size from 1 cm to 18 m. 18 m then equals 18 x 100 or 1800 cm. ∴ The length of large fish exceeds that of little fish by 1800 times.
How many parrotfish purchased by Carlos?The number of parrotfish Carlos purchased is represented by the variable y, whereas the number of angelfish Carlos purchased is represented by the variable x.
To know more about Fish visit:-
brainly.com/question/29657983
#SPJ4
Which linear inequality represents the graph below?
O A. y >
(-3, 3)
x + 1
6
Click here for long description
B. y ≥
x + 1
C. y ≥-3x+1
O D.y > x + 1
(0, 1)

Answers
Based on the given options, the linear inequality that represents the graph below is C. y ≥ -3x + 1
To determine the correct option, we need to analyze the characteristics of the graph. Looking at the graph, we observe that it represents a line with a solid boundary and shading above the line. This indicates that the region above the line is included in the solution set.
Option A, y > (-3/6)x + 1, does not accurately represent the graph because it describes a line with a slope of -1/2 and a y-intercept of 1, which does not match the given graph.
Option B, y ≥ x + 1, also does not accurately represent the graph because it describes a line with a slope of 1 and a y-intercept of 1, which is different from the given graph.
Option D, y > x + 1, is not a suitable representation because it describes a line with a slope of 1 and a y-intercept of 1, which does not match the given graph.
Only Option C. y ≥ -3x + 1.
This is because the graph appears to be a solid line (indicating inclusion) and above the line, which corresponds to the "greater than or equal to" relationship. The equation y = -3x + 1 represents the line on the graph.
Consequently, The linear inequality y -3x + 1 depicts the graph.
for such more question on linear inequality
https://brainly.com/question/17448505
#SPJ8
Write a multiplication expression without exponents that is equivalent to 3^3.
Answers
Hi! I'm happy to help!
This expression is an exponent, or repeated multiplication. 3^3 is three multiplied by itself (3), 3 times, or 3×3×3
So, our non-exponent expression will be 3×3×3.
I hope this was helpful, keep learning! :D
What is the coefficient of y in the expression 2x4+3y
Answers
Answer:
3
Step-by-step explanation:
Identify the point corresponding to Q.
A (-3,-2)
B (1,-1)
C (-3,2)
D (-2,-1)

Answers
Answer:
C (-3,2)
Step-by-step explanation:
Well point Q on the parabola is located on point (1,2),
The corresponding point means the point located all the way to the left of Q which is (-3,2).
Thus,
the point that is corresponding to point Q is C. (-3,2).
Hope this helps :)
A manager at a theater needs to order 267 new seats if the seats are sold only in groups of 10 what is the least number of seats that the manager should order
Answers
The least number of seats the manger could order to 270 seats
How to find the least number of seats the manger could orderThe information that the the seats are sold only in groups of 10 will help to know that the order will be in a multiple of 10.
The manager wants to order 267 seats and this is not a multiple of 10 the nearest multiple of 10 is 270.
This is because, 260 will be short of want the manager want however ordering for 270 will be in excess with three seats.
Hence the manager will order 270 and heave 3 extra seats
Learn more about multiples at:
https://brainly.com/question/26856218
#SPJ1
DOES ANYONE KNOW THE ANSWER

Answers
Answer:
D. none
Step-by-step explanation:
we only know about the right angle at the bottom right.
that is not enough information.
we always need 3 pieces of confirmed information of each triangle to be able to say that the 2 triangles are indeed of the same shape and size.
like the other answer options would indicate :
SAS : side - angle - side.
2 sides and the enclosed angle. if we know they are equal, then the rest of the triangles follow automatically.
SSS : all 3 sides. with 3 defined sides there is only one possible shake and size for that triangle.
HL : Hypotenuse and a leg of a right-angled triangle (also 3 pieces of information - 2 sides and the right angle).
since we have only the right angle and nothing else, we cannot prove that the triangles are congruent.
Write an equation in Ax+By=C form for this line.

Answers
9514 1404 393
Answer:
5x -2y = 30
Step-by-step explanation:
The slope of the line ...
Ax +By = C
is -A/B. This means we can use A=5 and B=-2 in the equation we're looking for. The value of C will be one that makes the equation true at the given point.
5x -2y = 5(4) -2(-5)
5x -2y = 30

find all the roots of x^3-5x^2-7x+51 if one root is 4-i
Answers
Answer:
Hello,
Step-by-step explanation:
P(x)=x^3-5x^2-7x+51
Since the coefficients are all reals,
4+i (conjugate of 4-i) is also a root.
The polynomial est divisible by (x-4-i)(x-4+i)=(x-4)²+1=x²-8x+17
If we divide P(x) by x²-8x+17 we find the quotient (x+3) and the remainder 0
P(x)=(x+4)(x-4-i(x-4+i)
Roots are -4,4+i and 4-i
Answer:
All the roots are -3, 4-i and 4+i.
Step-by-step explanation:
If oine root is 4 - i then another one is 4 + i as complex roots occur as conjugate pairs.
(4 - i)(4 + i)
= 16 - i^2
= 17.
As the last term = 51 = 3 * 17
looks like the other root is 3 or -3.
By the Factor theorem
If x = 3 then f(3) = 0
f(3) = 27 - 5(3)^2 - 7(3) + 51
= 27 - 45 - 21 + 51 = 12 so 3 is not a root.
If x = -3:
f(-3) = -27 - 45 _ 21 + 51
= 0
So, x = -3 is a root.
What is the sum of 17.25 and 1.725 , to the nearest integer?
Answers
The sum of 17.25 and 1.725, to the nearest integer, is 19.
First, let's add the two numbers together: 17.25 + 1.725 = 19.975
Next, we need to round the sum to the nearest integer. To do this, we need to look at the tenths place of the number. Since the tenths place is a nine, we need to round up to the nearest integer.
In this case, the nearest integer is 19.
To check our answer, we can add the two numbers together again using a calculator and confirm that the answer is 19.
To make sure we understand how to round to the nearest integer, let's look at another example. If we add 3.45 + 2.735, the sum is 6.185.
Looking at the hundredths place, we see that it is a five. Since five is greater than or equal to five, we need to round up to the nearest integer.
In this case, the nearest integer is 7.
To check our answer, we can add the two numbers together again using a calculator and confirm that the answer is 7.
In summary, to round a number to the nearest integer, we need to look at the tenths place. If the tenths place is greater than or equal to five, we round up to the nearest integer. If it is less than five, we round down to the nearest integer.
Therefore, the sum of 17.25 and 1.725, to the nearest integer, is 19.
To learn more about integer visit:
https://brainly.com/question/929808
#SPJ4
The sum of 17.25 and 1.725 is 18.975. To the nearest integer, this number is rounded up to 19.
Rounding to the nearest integer involves finding the closest whole number to a decimal or fractional number. When the decimal portion of a number is greater than or equal to 0.5, the number is rounded up to the next whole number. When the decimal portion of a number is less than 0.5, the number is rounded down to the previous whole number. In this case, the decimal portion of 18.975 is greater than 0.5, so the number is rounded up to 19.
Learn more about Sum:
https://brainly.com/question/28421287
#SPJ4
6) Choose what postulate proves the triangles congruent. *
SSS
SAS
X is the MidPoint Of QS, X IS the MidPoint Of RP
ASA
AAS
P
HL
X
R

Answers
Answer:
Step-by-step explanation:
The postulate that can be used to prove that triangle QXP and triangle SXR are congruent to each other is: SAS Congruence Theorem,. Recall:.
Hill co. Can further process product o to produce product p. Product o is currently selling for $60 per pound and costs $42 per pound to produce. Product p would sell for $82 per pound and would require an additional cost of $13 per pound to produce.
Answers
The Hill Co. should not further produce Product P from Product P.
We need to calculate the incremental cost and incremental revenue of producing P to understand the profit or loss margin.
Incremental revenue = Selling product of P - Selling product of O
Incremental revenue = 82 - 60
Performing subtraction
Incremental revenue = $22
Incremental cost = Cost of producing O - Cost of producing P
Incremental cost = 42 - 13
Performing subtraction
Incremental cost = $29
It is clear that incremental cost is more than incremental revenue, so Hill Co. should not continue the production.
Learn more about incremental cost -
https://brainly.com/question/25811981
#SPJ4
If a 10 kg ball is sitting on a 5 meter high ledge, what is it's potential energy? (g= 9. 8 m/s2)
Answers
Potential energy stored in the ball is 490 joule.
What is Potential Energy ?Potential energy is the power that an item may store due to its position in relation to other things, internal tensions, electric charge, or other factors.
Potential energy is a form of stored energy that is dependent on the relationship between different system components. When a spring is squeezed or extended, its potential energy increases.
The energy that an item has or acquires when its location changes as a result of being in a gravitational field is known as gravitational potential energy. Gravitational potential energy may be defined as an energy that has a connection to gravitational force or gravity.
Potential energy stored in the ball is given by ,
P.E = mgh = 10*9.8*5 = 490 joule.
To learn more about Potential Energy refer to :
https://brainly.com/question/16456713
#SPJ4
The __________ function in Excel is used to compute the statistics required to create a histogram.
a. FREQUENCY
b. RAND
c. NORM.INV
d. STDEV.S
Answers
The function in Excel that is used to compute the statistics required to create a histogram is the FREQUENCY function.
The FREQUENCY function is used to calculate how often values occur within a specified range or bin.
The output of the function is an array of values that represents the frequency distribution of the data, which can then be plotted to create a histogram.
To use the FREQUENCY function, we first need to define the bins or intervals that we want to use for our histogram.
These bins should cover the range of the data and should be of equal width.
Once we have defined our bins, we can use the FREQUENCY function to calculate the frequency of values that fall within each bin.
The syntax of the FREQUENCY function is as follows:
=FREQUENCY(data_array, bins_array)
The data_array argument is the array or range of data that we want to analyze, and the bins_array argument is the array or range of bins that we have defined.
The function returns an array of values that represents the frequency of values that fall within each bin.
Once we have the frequency distribution of our data, we can create a histogram by plotting the frequency values against the bin intervals.
Excel has built-in tools for creating histograms, which can be found under the "Data Analysis" menu.
By defining our bins and using the FREQUENCY function, we can quickly and easily analyze the distribution of our data and visualize it in a histogram.
For similar question on statistics:
https://brainly.com/question/31577270
#SPJ11
suppose a research report states that the result of a between subjects one-way anova is f (3, 32) = 3.47 should the researcher reject the null hypothesis if using alpha = .05
Answers
Based on the given information, the researcher should not reject the null hypothesis if using an alpha level of 0.05.
In hypothesis testing, the null hypothesis is typically assumed to be true until there is sufficient evidence to reject it. To determine whether to reject the null hypothesis, researchers often compare the calculated F-value from an ANOVA test with the critical F-value. The critical F-value is based on the significance level (alpha) chosen for the test. In this case, the given F-value is 3.47 with degrees of freedom (3, 32), indicating that there are three groups and a total of 32 observations. To make a decision, the researcher needs to compare the calculated F-value to the critical F-value. If the calculated F-value is greater than the critical F-value, the null hypothesis is rejected. However, if the calculated F-value is less than or equal to the critical F-value, the null hypothesis is not rejected. Since the critical F-value corresponding to alpha = 0.05 is not provided in the question, we cannot determine whether the null hypothesis should be rejected.
Learn more about ANOVA test here: https://brainly.com/question/30457832
#SPJ11
A 4 metre long ladder is placed against a wall. The angle between the ladder and
the ground is 75°. How far up the wall does the ladder reach?
How do you do this?
Answers
Answer:3.86 m
Step-by-step explanation:
Given
Length of ladder L=4 m
angle made by ladder and the ground is \(\theta=75^{\circ}\)
we will use trigonometry here
from the figure, we can write
\(\sin 75^{\circ}=\dfrac{x}{L}\quad [\text{where, x=distance of the ladder from the ground}]\)
\(\Rightarrow x=L\sin 75^{\circ}\\\Rightarrow x=4\sin 75^{\circ}=3.86\ m\)

Suppose a business records the following values each day the total number of customers that day (X) Revenue for that day (Y) A summary of X and Y in the previous days is mean of X: 600 Standard deviation of X: 10 Mean of Y: $5000, Standard deviation of Y: 1000 Correlation r= 0.9 Calculate the values A,B,C and D (1 mark) Future value of X Z score of X Predicted y average of y+ r* (Z score of X)* standard deviation of y 595 A B 600 0 $5000 D 615 IC You will get marks for each correct answer but note you are encouraged to show working. If the working is correct but the answer is wrong you will be given partial marks
Answers
The predicted values of A, B, C, and D are: A = 595B = -0.5C = 600D = $6350, therefore, the correct option is IC.
Given,
Mean of X = 600
Standard deviation of X = 10
Mean of Y = $5000
Standard deviation of Y = 1000
Correlation r= 0.9
Future value of X = 595
Z score of X = (X- Mean of X) / Standard deviation of X= (595-600) / 10 = -0.5
Using the formula, Predicted y = average of y+ r* (Z score of X)* standard deviation of y
Predicted y = $5000 + 0.9 * (-0.5) * 1000 = $4750
The predicted value of Y for X = 595 is $4750.
Now, to find the values of A, B, C, and D; we need to calculate the Z score of X = 615 and find the corresponding predicted value of Y.
Z score of X = (X- Mean of X) / Standard deviation of X= (615-600) / 10 = 1.5
Predicted y = average of y+ r* (Z score of X)* standard deviation of y
Predicted y = $5000 + 0.9 * (1.5) * 1000 = $6350
The predicted value of Y for X = 615 is $6350.
Hence, the values of A, B, C, and D are: A = 595B = -0.5C = 600D = $6350
Therefore, the correct option is IC.
learn more about predicted value here:
https://brainly.com/question/29745404
#SPJ11
what is 3x^2-x-2 factored?
Answers
To factor the quadratic expression 3x^2 - x - 2, we need to find two binomials that, when multiplied, give us the original expression.
The factored form of the quadratic expression can be determined by breaking down the middle term (-x) into two terms whose coefficients multiply to give the product of the coefficient of the squared term (3) and the constant term (-2). In this case, the product is -6. We are looking for two numbers whose sum is equal to -1 (the coefficient of the middle term) and whose product is equal to -6.
The numbers that satisfy these conditions are -3 and 2. We can now rewrite the expression using these numbers:
3x^2 - x - 2 = 3x^2 - 3x + 2x - 2
Next, we group the terms and factor by grouping:
(3x^2 - 3x) + (2x - 2) = 3x(x - 1) + 2(x - 1)
Now, we can see that we have a common binomial factor of (x - 1) in both terms. We can factor this out:
3x(x - 1) + 2(x - 1) = (3x + 2)(x - 1)
Therefore, the factored form of the quadratic expression 3x^2 - x - 2 is (3x + 2)(x - 1).
Who can help me get the answer??

Answers
Answer: 13,5 (first one)
Step-by-step explanation:According to given table for Relation g, we have following order pairs
(2,2)
(3,5)
(4,9)
(5,13)
Note: Each of first value in coordinate is x and each of the second value in the coordinate is y value.
We need to check the option, which gives an order pair of inverse relation of g.
In order to find inverse relation of a coordinate, we need to switch x and y values of a coordinate.
x value goes in y place and y value goes in x place.
So, the order pairs of inverse relation of given relation of g can be written as
(2,2) --> (2,2)
(3,5) --> (5,3)
(4,9) --> (9,4)
(5,13) --> (13,5).
In the given options, we have first order pair (13,5), which is the inverse of order pair (5,13).
Therefore, correct option is first option (13,5)
Define each of the 6 terms in the equations below and indicate their SI units Vxf = Vx₁ + axt xf = xi +vx₁t+ = 1/2 axt² v2xf = v2xt + 2ax (xf - xi) xi = Vx₁ = xf = ax = Vxf = t= a
The above equations represent what type of motion? b. What type of motion does the above equations represent when the acceleration is zero?
Answers
a. The equations represent the motion of an object undergoing constant acceleration in one dimension.
a. The equations represent motion with constant acceleration in one dimension. b. When the acceleration is zero, the equations represent motion with constant velocity or uniform motion.
1. Vxf = Vx₁ + axt: This equation relates the final velocity (Vxf) to the initial velocity (Vx₁), acceleration (a), and time (t). It indicates that the final velocity of an object is equal to the initial velocity plus the product of acceleration and time.
2. xf = xi + Vx₁t + 1/2 axt²: This equation gives the displacement (xf) of the object at time t. It relates the initial position (xi), initial velocity (Vx₁), time (t), and acceleration (a). It includes both the linear term (Vx₁t) and the quadratic term (1/2 axt²), which arises from the constant acceleration.
3. v2xf = v2xt + 2ax (xf - xi): This equation relates the squares of the final velocity (v2xf) and initial velocity (v2xt) to the acceleration (a), displacement (xf - xi), and the sign of the acceleration. It can be derived from the equations of motion and is useful for calculating the final velocity when the other variables are known.
When the acceleration (a) is zero:
If the acceleration is zero, then the equations simplify to:
- Vxf = Vx₁: The final velocity is equal to the initial velocity.
- xf = xi + Vx₁t: The displacement is determined by the initial position, initial velocity, and time, following constant velocity motion.
- v2xf = v2xt: The squares of the final velocity and initial velocity are equal. This equation also indicates constant velocity motion.
In summary, when the acceleration is zero, the equations represent motion with constant velocity or uniform motion.
Learn more about constant here: https://brainly.com/question/17550734
#SPJ11
Give asymptotic upper and lower bounds for T(n) (1) T(n) = 20T(n/9) + n1.5 (2). T(n) = 25T(n/625) + n0.66 = (3). T(n) = 15T(n/225) + n0.5 (4). T(n) = T(n-10) + n4.3
Answers
As a general rule, a recursion function is any function that takes its value by manipulating the previous terms in the function.
To determine the asymptotic upper and lower bounds for the given recursion functions, let's analyze each case separately:
(1) T(n) = 20T(n/9) + \(n^{1.5}\)
In this case, we can apply the Master Theorem to determine the asymptotic bounds. The Master Theorem states that if a recursive function is of the form T(n) = aT(n/b) + f(n), where a ≥ 1, b > 1, and f(n) is an asymptotically positive function, then:
If f(n) = Θ(\(n^{c}\)) for some constant c < logb(a), then T(n) = Θ(\(n^{logb(a)}\))).
If f(n) = Θ(\(n^{logb(a)}\) * \(log^{k(n)}\)) for some constant k ≥ 0, then T(n) = Θ\((n^logb(a) * log^(k+1)(n)).\)
If f(n) = Θ(\(n^{c}\)) for some constant c > logb(a), and if a * f(n/b) ≤ kf(n) for some constant k < 1 and sufficiently large n, then T(n) = Θ(f(n)).
In our case, a = 20, b = 9, and f(n) = \(n^{1.5}\)
Since logb(a) = log9(20) ≈ 1.1505 and c = 1.5, we have c > logb(a). Therefore, we can apply case 3 of the Master Theorem.
Now, we need to check if a * f(n/b) ≤ kf(n) for some constant k < 1 and sufficiently large n. Let's consider k = 1 and n ≥ 1.
20 * \((n/9)^{1.5}\) ≤ 1 *\(n^{1.5}\)
20/9 ≤ 1
Since 20/9 > 1, the condition is not satisfied for k = 1. Hence, we cannot apply the Master Theorem directly.
However, we can observe that grows faster than \((n/9)^{1.5}\), which means that the dominant term in the recursion is \(n^{1.5}\).
Therefore, we can approximate the upper bound as T(n) = O\((n^{1.5})\).
(2) T(n) = 25T(n/625) + \(n^{0.66}\)
Similar to the previous case, let's apply the Master Theorem.
In this case, a = 25, b = 625, and f(n) = \(n^{0.66}\)
logb(a) = log625(25) = 2/3, and c = 0.66. Since c < logb(a), we can apply case 1 of the Master Theorem.
Therefore, T(n) = Θ(\(n^{log625(25)}\)) = Θ(\(n^{(2/3)\)).
Hence, the asymptotic upper and lower bounds for T(n) are T(n) = O(\(n^{(2/3)\)) and T(n) = Ω(\(n^{(2/3)\)).
(3) T(n) = 15T(n/225) + \(n^{0.5}\)
Using the same approach, we have a = 15, b = 225, and f(n) = \(n^{0.5}.\)
logb(a) = log225(15) ≈ 0.5727, and c = 0.5. Since c < logb(a), we apply case 1 of the Master Theorem.
Hence, T(n) = Θ\((n^{log225(15)})\) = Θ(\(n^{0.5727})\).
Therefore, the asymptotic upper and lower bounds for T(n) are T(n) = O\((n^{0.5727})\)and T(n) = Ω(\(n^{0.5727}\)).
(4) T(n) = T(n-10) + \(n^{4.3}\)
In this case, we don't have a direct recurrence relation. However, we can observe that the function T(n) is recursive based on the value T(n-10) and grows with the term \(n^{4.3}.\)
Since there is no division or constant factor in the recursive part, we can assume that the dominant term is \(n^{4.3}.\)
Therefore, the upper and lower bounds for T(n) can be approximated as T(n) = O(\(n^{4.3}.\)) and T(n) = Ω\(n^{4.3}\).
Learn more about asymptotic bounds here:
https://brainly.com/question/30425942
#SPJ11
kate plays on her schools basketball team last season she made 70% of her 50 free throw attempts how is 70% expressed as a fraction
A.7/1
B.50/70
C. 70/50
D.70/100
PLEASE HELP
Answers
Answer:
D
Step-by-step explanation:
70% as a fraction is 70/100
Answer:
The answer would be D. 70/100
Step-by-step explanation:
70% as a fraction is 70/100
The fact that she threw 50 free throws last season is not important because the question does not ask for the amount of shots she made.
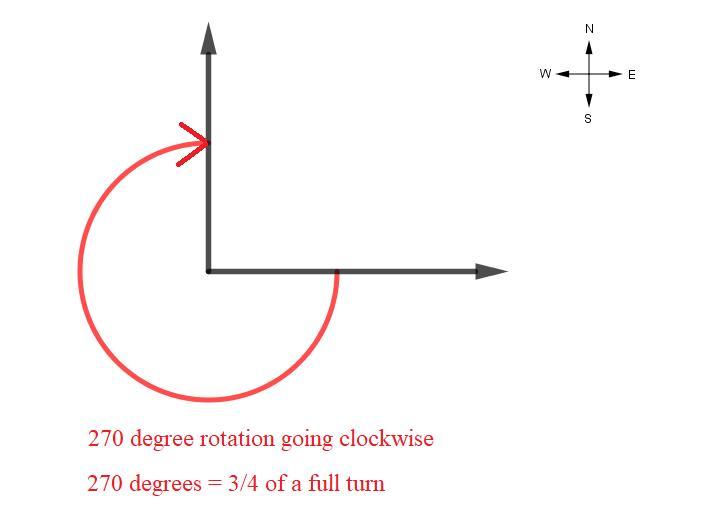
Rick is facing east.He makes three-quarters of complete turn clockwise.Which direction is Rick now facing?
Answers
Answer: directly north
=============================================
Explanation:
A one quarter turn is 1/4 of 360 degrees, so it's (1/4)*360 = 90 degrees.
Three quarters of a full turn is (3/4)*360 = 270, or you could triple the 90 to get 90*3 = 270.
Rick starts facing directly east. Then he rotates 270 degrees clockwise to end up facing directly north. Refer to the diagram below.
a)P+(2x^2-y^2-xy)=5x^2-y^2-2xy b)Q-(x^2-2x-15)=-3x^2+7-4x
Answers
a) The equation is P + (2x^2 - y^2 - xy) = 5x^2 - y^2 - 2xy. To solve for P, we need to isolate it on one side of the equation. We can do this by adding y^2 + xy - 3x^2 to both sides:
P + (2x^2 - y^2 - xy) + y^2 + xy - 3x^2 = 5x^2 - y^2 - 2xy + y^2 + xy - 3x^2
Simplifying this expression, we get:
P - x^2 = 2xy
Finally, we can solve for P by adding x^2 to both sides:
P = 2xy + x^2
b) The equation is Q - (x^2 - 2x - 15) = -3x^2 + 7 - 4x. To solve for Q, we need to isolate it on one side of the equation. We can do this by adding (x^2 - 2x - 15) to both sides:
Q - (x^2 - 2x - 15) + (x^2 - 2x - 15) = -3x^2 + 7 - 4x + (x^2 - 2x - 15)
Simplifying this expression, we get:
Q = -2x^2 - 2x - 8
Therefore, the solution to the system of equations is:
P = 2xy + x^2
Q = -2x^2 - 2x - 8
To know more about Equation, visit:
https://brainly.com/question/29657983
#SPJ11