There are two approaches to solving the equation -3x + 10 = 4x - 20
Subtract 4x from both sides. OR Add 3x to both sides.
–7x + 10 = –20 OR 10 = 7x – 20
Solve the equation using both approaches.
What is the solution?
Answers
Related Questions
For a fund-raiser, Anthony earns $5 for the first mile he runs, an additional $7 for the second mile, an additional $9 for the third mile, and so on.The expression represents the total amount of money Anthony earns if he runs 10 miles. How much does Anthony earn if he runs 10 miles?
Answers
Answer:
He will earn $140, my bad miss calculated...
Step-by-step explanation:
Its 140....
What are the minimum and maximum temperatures recorded in this table?
Temperature (°C) 11 0 24.2 -32.4 -0.6 0.5
Answers
The minimum temperature recorded is -32.4°C and the maximum temperature is 24.2°C, as seen by basic comparison of values.
What is comparison of values?The process of comparison of numbers establishes the similarities between two numbers and determines which number is greater, smaller, or equal to another number.
Now, given values :11.0, 24.2, -32.4, -0.6, 0.5
Arranging them in ascending order: -32.4, -0.6, 0.5, 11.0, 24.2Thus, The minimum temperature recorded is -32.4°C and the maximum temperature is 24.2°C, as seen by basic comparison of values.
To learn more about comparison of values, refer to the link: https://brainly.com/question/1668435
#SPJ9
Which point is between points C and E?
Answers
Answer:
point D
Step-by-step explanation:
Find the midpoint of the segment with the following endpoints. (10, 10) and (2, 6)
Answers
Answer:
(6, 8 )
Step-by-step explanation:
given endpoints (x₁, y₁ ) and (x₂, y₂ ) then the midpoint is
( \(\frac{x_{1}+x_{2} }{2}\) , \(\frac{y_{1}+y_{2} }{2}\) )
here (x₁, y₁ ) = (10, 10 ) and (x₂, y₂ ) = (2, 6 ) , then
midpoint = ( \(\frac{10+2}{2}\) , \(\frac{10+6}{2}\) ) = ( \(\frac{12}{2}\) , \(\frac{16}{2}\) ) = (6, 8 )
the population of a city is expected to be people after years. find the average population between year and year .
Answers
The average population between year 1 and year 10 is approximately 55,555 people.
To find the average population between year X and year Y, we need to first calculate the total population increase over that time period. We can do this by subtracting the population in year X from the population in year Y.
Population increase = Population in year Y - Population in year X
Once we have the population increase, we can divide it by the number of years between X and Y to get the average annual population increase.
Average annual population increase = Population increase / (Y - X)
Finally, to find the average population between year X and year Y, we need to add the average annual population increase to the population in year X.
Average population = Population in year X + Average annual population increase
For example, if the population of a city is expected to be 100,000 people after 10 years, and we want to find the average population between year 1 and year 10, we would do the following:
Population in year 1 = X = 50,000 (let's say)
Population in year 10 = Y = 100,000
Population increase = 100,000 - 50,000 = 50,000
Number of years between X and Y = 10 - 1 = 9
Average annual population increase = 50,000 / 9 = 5,555.56 (rounded)
Average population = 50,000 + 5,555.56 = 55,555.56 (rounded)
Learn more about average here:
https://brainly.com/question/13365551
#SPJ11
The average population of the city between the starting year and 10 years later is estimated to be 625,000.
The average population of a city between two specific years, we will need to use the formula for calculating the arithmetic mean.
The sum of all the values divided by the number of values.
We will need to sum up the populations of the city for each year between the two given years and divide the result by the number of years included.
Let us assume that the population of the city in the year we are starting with is "P1" and the population after "n" years is "P2".
Therefore, the average population can be calculated as:
\(Average Population = (P1 + P2) / 2\)
The exact population figures for each year between the two given years, we will have to use an estimated population growth rate to make the calculation.
We can use the formula:
\(P2 = P1 \times (1 + r)^n\)
where "r" is the estimated annual growth rate and "n" is the number of years between the two given years.
Let's assume that the population of the city in the starting year is 500,000 and the estimated population after 10 years is 750,000. Using the formula, we can calculate the estimated annual growth rate as:
\(r = (P2 / P1)^{(1/n)} - 1 = (750,000 / 500,000)^{(1/10)} - 1 = 0.0473 or 4.73\%\)
The estimated annual growth rate, we can calculate the average population between the two given years using the formula:
\(Average Population = (P1 + P2) / 2 = (500,000 + 750,000) / 2 = 625,000\)
It is important to note that this is just an estimate based on the assumed growth rate, and the actual population may vary from this calculation.
For similar questions on Average Population
https://brainly.com/question/28103278
#SPJ11
suppose c=[1 2],d=[4 0]. [2 5] [ 0 1]
if a=CDC^−1, use diagonalization to compute A^4. [ ___ ___ ]
___ ___
Answers
The solution of above equation is
[ 0 81/3 ]
To find the matrix A, we need to compute the inverse of C times D times C:
C^(-1) = [-2 1]
[ 1 0]
CDC^(-1) = [1 2][-2 1][4 0] = [4 -4]
[0 1]
Now we need to diagonalize A^4. First, let's find the eigenvalues of A:
|A - lambda*I| = 0
|4-lambda -4 | |lambda 0 |
|0 1-lambda| * |-4 1-lambda| = 0
Expanding the determinant, we get:
(4 - lambda)(1 - lambda) - 4*0 = 0
=> lambda^2 - 5*lambda + 4 = 0
=> (lambda - 4)*(lambda - 1) = 0
Therefore, the eigenvalues of A are λ1 = 4 and λ2 = 1. Now, let's find the eigenvectors associated with each eigenvalue:
For λ1 = 4:
(A - 4*I)x = 0
[(4 - 4) -4 ] [x1] [0]
[ 0 (1-4) ] [x2] = [0]
=> -4*x2 = 0
=> x2 = 0
Any value of x1 will satisfy the equation, so we can choose x1 = 1:
eigenvector v1 = [1 0]'
For λ2 = 1:
(A - I)x = 0
[(4 - 1) -4 ] [x1] [0]
[ 0 (1-1) ] [x2] = [0]
=> 3*x1 - 4*x2 = 0
=> x1 = (4/3)*x2
We can choose x2 = 3:
eigenvector v2 = [4 3]'
Now we can construct the diagonal matrix Λ with the eigenvalues on the diagonal:
Λ = [4 0]
[0 1]
And the matrix P with the eigenvectors as columns:
P = [1 4]
[0 3]
To compute A^4, we use the formula A^4 = P*Λ^4*P^(-1):
P^(-1) = (1/(13 - 40)) [ 3 -4]
[ 0 1]
Λ^4 = [4^4 0 ]
[0 1^4]
P^(-1) = (1/3) [ 3 -4]
[ 0 1]
A^4 = PΛ^4P^(-1) = [1 4][256/3 0 ][ 3 -4] = [4096/3 - 16384/3]
[0 3][ 0 1] [ 0 1] [ 0 81/3 ]
Therefore, the answer is:
[4096/3 -16384/3]
[ 0 81/3 ]
Click the below link, to learn more about Matrices:
https://brainly.com/question/28180105
#SPJ11
What number is 40% of 160?
Answers
Answer:
64
Step-by-step explanation:
40% of 160 is the same as 160% of 40. You can divide each number by 100 to get an answer.
Answer:
64
Step-by-step explanation:
When finding percentages, you have to multiply the whole number by the percent in fractional form. In this example:
\(160*0.4=64\)
Hope this helped!! :)
An item originally priced at $75 is marked 40% off. What is the sale price?
Answers
Answer:
$45
Step-by-step explanation:
What is an equation of the line that passes through the point
(−3,−5) and is parallel to the line
2x+3y=15
Answers
Therefore, the equation of the line passing through (-3, -5) and parallel to the line 2x + 3y = 15, in slope-intercept form, is y = (-2/3)x - 7.
What is the Equation of Parallel Lines?To find the equation of a line parallel to the line 2x + 3y = 15 and passing through the point (-3, -5), we need to determine the slope of the given line and use it to construct the equation in slope-intercept form (y = mx + b).
The given line is in the form Ax + By = C, where A = 2, B = 3, and C = 15. To find the slope of this line, we can rearrange the equation to isolate y:
2x + 3y = 15
3y = -2x + 15
y = (-2/3)x + 5
The slope of the given line is -2/3.
Since the line we want to find is parallel to this line, it will have the same slope. Therefore, the slope of the line passing through (-3, -5) will also be -2/3.
Now, we can use the point-slope form of a linear equation to write the equation of the line:
y - y1 = m(x - x1)
Substituting the values of (-3, -5) and -2/3 for (x1, y1) and m, respectively:
y - (-5) = (-2/3)(x - (-3))
y + 5 = (-2/3)(x + 3)
To convert this equation into slope-intercept form, we can simplify and rearrange:
y + 5 = (-2/3)x - 2
y = (-2/3)x - 2 - 5
y = (-2/3)x - 7
Learn more about Equation of Parallel Lines on:
https://brainly.com/question/11345748
#SPJ1
Choose all of the conversions that are true for the capacity of the pitcher of orange juice.
Pitcher filled with 3.5 litres of orange juice.
A. 0.35 kL
B. 0.035 kL
C. 0.0035 kL
D. 3,500 mL
E. 350 mL
Answers
Answer:
C and D
Step-by-step explanation:
Kil represents one thousand, and milli represents one thousandth.
14.
Jeremy can build a model airplane in 5 hours less time than his brother. Working together they need 6 hours to build the plane. How long would
it take Jeremy to build the model airplane working alone?
Answers
To work together, their combined work rate is the sum of their individual work rates. So we have:
1/x + 1/(x-5) = 1/6
We can solve for x, the number of hours it would take Jeremy's brother to build the model airplane alone:
6(x)(x-5) = x(x-5) + x(6)
Simplifying this expression, we get:
6x^2 - 30x = x^2 - 5x + 6x
5x^2 - 31x = 0
x = 31/5
So it would take Jeremy's brother 6 hours and 12 minutes to build the model airplane alone.
Since we know Jeremy can build it in 5 hours less time, it would take him 31/5 - 5 = 6 1/5 - 5 = 1 1/5 or 1 hour and 12 minutes to build the model airplane working alone.
a company's _______ function is the money generated by selling x units of its product. the difference between this function and the company's cost function is called its ________ function.
Answers
(a) how many 4-permutations are there of a set of five objects? (b) how many 2-permutations are there of a set of nine objects?
Answers
(a) 4-permutations of a set of five objects is 120 without repetition and 625 with repetitions.
(b) 2-permutations of a set of nine objects is 72 without repetition and 81 with repetitions.
A permutation is a choice of r things out of a set of n options where the order in which we choose our items is important. It's denoted by nPr.
It can be of two types:
Without Repetition: nPr= \(\frac{n!}{(n-r)!}\)
With Repetition: nPr= \(n^{r}\)
(a) 4-permutations of a set of five objects:
here, n=5 and r=4
Without repetitionnPr= \(\frac{n!}{(n-r)!}\)
= \(\frac{5!}{(5-4)!}\)
= \(\frac{5!}{1!}\)
= 120
With repetitionnPr= \(n^{r}\)
= \(5^{4}\)
= 625
(b) 2-permutations of a set of nine objects:
here, n=9 and r=2
Without repetitionnPr= \(\frac{n!}{(n-r)!}\)
= \(\frac{9!}{(9-2)!}\)
= \(\frac{9!}{7!}\)
= 72
With repetitionnPr= \(n^{r}\)
= \(9^{2}\)
= 81
To learn more about permutations,
visit; brainly.com/question/1216161
#SPJ4
Gravel is being dumped from a conveyor belt at a rate of 25 ft3/min, and its coarseness is such that it forms a pile in the shape of a cone whose base diameter and height are always equal. How fast (in ft/min) is the height of the pile increasing when the pile is 11 ft high
Answers
When the pile of gravel, in the shape of a cone with equal base diameter and height, reaches a height of 11 feet, the height of the pile is increasing at a rate of 60/121π feet per minute. This rate indicates how fast the height of the pile is increasing at that specific height.
Let the height and radius of the cone be h and r respectively. Then the volume V of the cone is given by; V = 1/3 πr²h. Also given, the coarseness is such that the base diameter and height are always equal. Therefore, r = h/2. Also, given that gravel is being dumped at a rate of 25 ft³/min. The rate of change of volume with respect to time is given by; dV/dt = 25 ft³/min.
We need to find the rate at which the height of the pile is increasing when the height of the pile is 11 feet. Now we will find the relation between V and h;
V = 1/3 πr²hV = 1/3 π(h/2)²hV = 1/12 πh³.
Now differentiate both sides of the equation with respect to time;
dV/dt = d/dt (1/12 πh³)
dV/dt = 1/4 πh² dh/dt
From equation (1); dV/dt = 25 ft³/min
dV/dt = 1/4 πh²
dh/dt25 = 1/4 π(11/2)² dh/dt
dh/dt = 60/121π feet per minute.
Therefore, the height of the pile is increasing at a rate of 60/121π feet per minute when the height of the pile is 11 feet.
The concept used to solve this problem is related rates.
In related rates problems, we are given the rates at which certain variables are changing and we are asked to find the rate at which another variable is changing. To solve such problems, we typically set up an equation that relates the variables and then differentiate both sides of the equation with respect to time.
Learn more about differentiation at:
brainly.com/question/954654
#SPJ11
This data set is ages at first job. 14, 14, 16, 16, 17, 17, 18, 20, 21, 23 Construct a boxplot. Make sure to include labels.
Answers
Answer:
Please find attached the required box and whiskers plot
Step-by-step explanation:
The numbers are given in arranged order as follows;
14, 14, 16, 16, 17, 17, 18, 20, 21, 23
The five number summary are;
The minimum value = 14
The maximum value = 23
The first quartile, Q₁, is the (n + 1)/4th term or the 2.75th term = 14 + 0.75×(16 - 14) = 15.5
The second quartile, Q₂, (the median) is the (n + 1)/2th term or the 5.5th term = 17
The third quartile, Q₃, is the 3(n + 1)/4th term or the 8.25th term = 20 + 0.25×(21 - 20) = 20.25.

suppose each license plate in a certain state has three letters followed by three digits. the letters and and the digits , , and are not used. so, there are letters and digits that are used. assume that the letters and digits can be repeated. how many license plates can be generated using this format?
Answers
With the possibility of repeating letters and digits, the total number of license plates that can be generated in this format is 8,000,000.
In a state where license plates consist of three letters followed by three digits, with the exclusion of three specific letters and three specific digits, there are a total of 20 letters and 7 digits available for use.
The number of possibilities for each position on the license plate can be calculated by multiplying the number of options for each position. For the letters, since three letters are chosen from a set of 20 (excluding the three specified letters), with repetition allowed, the number of possibilities is 20^3 = 8,000. Similarly, for the digits, since three digits are chosen from a set of 7 (excluding the three specified digits), with repetition allowed, the number of possibilities is 7^3 = 343. To find the total number of license plates, we multiply these two results together: 8,000 * 343 = 2,744,000. Therefore, there are a total of 2,744,000 possible license plates.
Learn more about digits here:
https://brainly.com/question/18793452
#SPJ11
Which of the following shows the true solution to the logarithmic equation below? log (x) log (x 5) = log (6 x 12).
Answers
Anti-log and log a + log b = log ab is used. Then the true solutions of the logarithmic equation are 4 and -3.
What is a logarithm?Logarithms are another way of writing exponent. A logarithm with a number base is equal to the other number. It is just the opposite of the exponent function.
The logarithmic equation is given below;
log (x) + log (x + 5) = log (6x + 12)
We know that log a + log b = log ab, then we have
log (x) + log (x + 5) = log (6x + 12)
log (x)(x + 5) = log (6x + 12)
log (x² + 5x) = log (6x + 12)
Take anti-log, then we have
x² + 5x = 6x + 12
x² - x - 12 = 0
On factorizing, we have
x² - x - 12 = 0
x² - 4x +3x - 12 = 0
x (x - 4) + 3(x - 4) = 0
(x - 4)(x + 3) = 0
x = 4, -3
Thus, the true solutions of the logarithmic equation are 4 and -3.
More about the logarithm link is given below.
https://brainly.com/question/7302008
Answer: true solutions of the logarithmic equation are 4 and -3.
Step-by-step explanation:
I took the edu pre-test -22
Helppppp pleaseeee anyoneeeeeee!!!!!!!!!!!!!
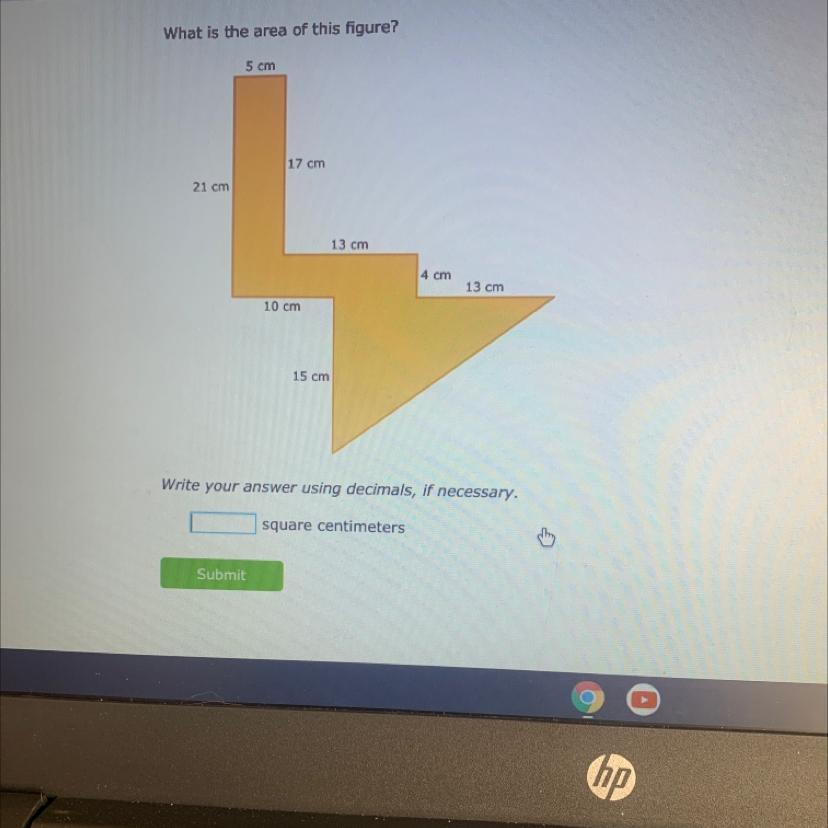
Answers
Explanation
Divide the areas into conventional shapes with determined formulas, rectangles, triangles and add them together
(17x5)+(18x4)+(21x15/2)
= 314.5
Hope this helps :)
The length of a rectangle is 3 less than 4 times
the width. The perimeter is 34. Find the length
and width.
Let
x = width
4x-3 = length
w=x
P = 2w + 2L
34 = 2x + 2(4x-3)
L=4x-3
Answers
→ Perimeter = 2( Length + Width)
→34 = 2x + 2(4x-3)
→34 = 2x + 8x - 6
→34 = 10x -6
→10x = 34 +6
→10 x = 40
→x = 40/10
→x = 4
Width is 4 unit and length is (4*4 -3) = 13 unit.Hope this helped you!
what prefix multiplier is appropriate for reporting a measurement of 5.57 ×10−5 m?
Answers
To determine the appropriate prefix multiplier for reporting a measurement of 5.57 × 10^(-5) m, we need to find a suitable metric prefix that would make the number easier to read and understand.
1. Convert the original measurement (5.57 × 10^(-5) m) to a more suitable metric unit.
2. Compare the metric prefixes and their corresponding multipliers to find the best fit.
In this case, the closest metric prefix for 10^(-5) is "micro" (symbol: µ), which has a multiplier of 10^(-6). To use this prefix, we need to convert the measurement to micrometers (µm).
3. Divide the original measurement by the multiplier of the chosen prefix: (5.57 × 10^(-5) m) / (10^(-6) µm/m) = 55.7 µm.
So, the appropriate prefix multiplier for reporting the measurement of 5.57 × 10^(-5) m is "micro," and the measurement can be reported as 55.7 µm.
Learn more about it here:
brainly.com/question/31645196
#SPJ11
A computer company has the following Cobb-Douglas production function for a certain product: p(x, y) = 800x³/43/4 where x is the labor, measured in dollars, and y is the capital, measured in dollars. Suppose that the company can make a total investment in labor and capital of $1000000. How should it allocate the investment between labor and capital in order to maximize production?
Answers
Where the above cobb-douglas function is given, to maximize production,the company should allocate $750,000 tolabor (x) and $250,000 to capital ( y).
Why is this so ?We solved using the LaGrange multipliers.
Setting up the LaGrange function -
L(x, y, λ) = p(x, y) - λg(x, y)
L(x, y, λ) =800x^(3/4)y^( 1/4)- λ(x + y - $ 1,000,000)
Take the partial derivatives -
∂L/∂x = 600x^(-1/4) y^(1/4) - λ = 0
∂L /∂y = 200x^(3/4)y^(-3/4) - λ = 0
∂L/∂λ = -(x + y - $1,000,000 ) = 0
Equate these two expressions
600 x^(-1/4)y^(1/4)= 200x^(3/ 4)y^(-3/4)
3y = x
Substituting this relationship into the constraint equation x + y = $1,000,000 -
3y + y = $ 1,000,000
4y= $1,000,000
y = $250,000
Substituting y = $250,000
3y = x
3 ($250,000) = x
x = $ 750,000
Hence the production maximizing ratio between labor and capital is
Labor - $750,000 : Capital $ 250,000
Learn more about production function:
https://brainly.com/question/13564389
#SPJ1
Full question:
A computer company has the following Cobb-Douglas production function for a certain product: p(x, y) = 800x^(3/4)y^(1/4) where x is the labor, measured in dollars, and y is the capital, measured in dollars. Suppose that the company can make a total investment in labor and capital of $1000000. How should it allocate the investment between labor and capital in order to maximize production?
Please help!!!
Figure A below is translated 4 units left and 1 unit down and then reflected over the y-axis.
Which best explains whether figure B is the image of figure A under the specified transformations?
Figure B is not the image of figure A because the triangles are not congruent.
Figure B is not the image of figure A because the transformations were performed in an incorrect order.
There is not enough information to determine whether figure B is the image of figure A after the transformations.
Figure B is the image of figure A. The transformations were performed correctly.

Answers
D. Figure B is the image of figure A. The transformations were performed correctly.
What is the geometry and transformation?
Geometry transformation refers to the process of changing the position, orientation, and/or size of a geometric shape.
To determine and prove whether the image of figure A is figure A after the given transformation you can work graphically or analytically.
To show you I will work analytically, as the graphical method is hard to explain without a video.
So:
1) First, translation 4 units left and 1 unit down means:
(x,y) → (x - 4, y - 1), so any point (a,b) will be transformed into a point (a - 4, b - 1).
2) Second, reflection over the y-axis means:
(x,y) → (-x,y).
So, point (a - 4, b - 1) will be transformed into a point (4 - a, b - 1)
3) Check what happens with the vertices of figure A, using the last relation (a,b)→(4 - a, b - 1)
vertex (5, -2) → (4 - 5, -2 - 1) = ( -1, -3)
vertex (5, -3) → (4 - 5, -3 - 1) = ( -1, -4)
vertex (2, - 4) → (4 - 2, -4 - 1) = (2, - 5).
As you can see in the figure, the points (-1, -3), (-1, -4), and (2, -5) are the vertices of triangle B, which shows that the transformations yield the figure A to figure B.
To learn more about geometry transformation, Visit
https://brainly.com/question/28176181
#SPJ1
Write a Matlab function called euler_timestep that solve the IVP dy/dt = f(t,y), a≤t≤b, y(0)=α using Euler's timestepping method. The header should look like function y - euler_timestep (f,a,b,alpha,N)
where N is the number of intervals used, so that Δt = b-a/N. Note that the output should be an array that contains the evaluation of the solution at all time steps. Use this method to solve the IVP dy/dt = (sin(2t) - 2ty)/t², y(1)=2, t = [1,5]
with N = 10, 10², 10³, Call y0, y1, y2 the three results. Plot the three solutions with respect to t. On another figure, make a loglog plot of absolute error at t = 5 versus the number of intervals for all three methods on the same plot. To compute the exact solution use the matlab function dsolve Cody coursework might not recognize the function dsolve, compute it on Matlab and copy the expression on Cody. Comment on your results (using %): which method works best, which method works the worst? Why?
Answers
The Euler's timestepping method is implemented in the MATLAB function euler_timestep to solve the initial value problem (IVP) dy/dt = f(t,y), a≤t≤b, y(0)=α.
The function takes as input the function f, the interval [a,b], the initial value α, and the number of intervals N. It returns an array y that contains the solution evaluated at all time steps.
To solve the specific IVP dy/dt = (sin(2t) - 2ty)/t², y(1)=2 on the interval [1,5] with N = 10, 10², 10³, we can call the euler_timestep function three times with different values of N. Let's denote the solutions as y0, y1, and y2. We can then plot the three solutions with respect to t.
To compute the exact solution, we can use the MATLAB function dsolve to obtain the symbolic expression. However, since Cody coursework might not recognize dsolve, we need to compute the exact solution on MATLAB and copy the expression to Cody.
Finally, we can make a log-log plot of the absolute error at t = 5 versus the number of intervals for all three methods on the same plot. This allows us to compare the accuracy of the different methods.
In terms of the results, we can analyze which method works best and which works the worst by examining the accuracy of the solutions and the error plots. The accuracy can be evaluated by comparing the exact solution with the numerical solutions obtained using different values of N. The error plot will show how the error changes as the number of intervals increases for each method. Based on these observations, we can draw conclusions about the performance and effectiveness of each method in solving the given IVP.
To learn more about intervals click here:
brainly.com/question/11051767
#SPJ11
The um of three number i 50 the firt number i twice the econd number the third number i half the firt number
Answers
If the sum of three numbers is 50, it forms a linear equation that is x + y + z = 50. By solving this equation we can get the value of x, y and z.
The Equation is a mathematical statement with an 'equal to' symbol between two expressions that have equal values. There are different types of equations like linear, quadratic, cubic, etc. There are numerous ways in which one may define an equation. In its simplest form in algebra, the definition of an equation is a mathematical statement that shows that two mathematical expressions are equal. The most basic and simple algebraic equations consist of one or more variables in math.
The sum of three number is 50 the first number is twice the second number the third number is half the first number.
x + y + z = 50
x = 2y
z = x / 2
Here we form a linear equation. A linear equation may have more than one variable. A linear equation is an equation in which the highest power of the variable is always 1. It is also known as a one-degree equation. By solving this linear equation we can get the value of x, y and z.
To know more about Linear equation please visit:
https://brainly.com/question/12788590
#SPJ4
a circle has radius 13 centimeters. suppose an arc on the circle as length 6π centimeters. what is the measure of the central angle whose radii define the arc?
Answers
Therefore, the measure of the central angle whose radii define the given arc is approximately 83.077 degrees.
The length of an arc on a circle is given by the formula:
Arc Length = (Central Angle / 360°) * Circumference
In this case, we know the arc length is 6π centimeters, and the radius of the circle is 13 centimeters. The circumference of the circle can be calculated using the formula:
Circumference = 2π * Radius
Substituting the radius value, we get:
Circumference = 2π * 13
= 26π
Now we can use the arc length formula to find the central angle:
6π = (Central Angle / 360°) * 26π
Dividing both sides of the equation by 26π:
6π / 26π = Central Angle / 360°
Simplifying:
6 / 26 = Central Angle / 360°
Cross-multiplying:
360° * 6 = 26 * Central Angle
2160° = 26 * Central Angle
Dividing both sides by 26:
2160° / 26 = Central Angle
Approximately:
Central Angle ≈ 83.077°
To know more about central angle,
https://brainly.com/question/19784457
#SPJ11
The diagram shows a triangle. What is the value of z?

Answers
Answer:
z = 53
Step-by-step explanation:
Comment
The three angles of any triangle add up to 180o. There are no exceptions to this rule.
Formula
2z + z - 15 + 36 = 180 Combine like terms on the left.
Solution
3z + 21 = 180 Subtract 21 from both sides
3z + 21 - 21 = 180 - 21 Combine
3z = 159 Divide both sides by 3
z = 53
What is the slope of the line passing through points (4,6) and (2,3)?
Answers
Answer: 3/2
Step-by-step explanation: y2-y1/ x2- x1
Taylor works at a garden shop that sells flower pots. One kind of flower pot has a rim height of 6 centimeters and a planting height of 22 centimeters. Taylor begins to stack the flower pots as shown.
The table shows the height of each stack for the given number of flower pots.
Number of Flower Pots, n 1 2 3 4 5
Height of Stack in cm 28 34 40 46 52
Write a simplified algebraic expression to represent the height of a stack of n flower pots.
Answers
Answer:
The simplified algebraic expression to represent the height, h, of a stack in cm of n flower pots is h = 6·n + 22
Step-by-step explanation:
The given information are;
The rim height of one kind of flower pot = 6 cm
The planting height of the flower pot = 22 cm
Therefore, the total height of the flower pot = 22 + 6 = 28 cm
Stacking the flower pots of a single kind will give a linear relationship of the form, y = m·x + c between the height of the stack and the number of flower pots in the stack
Where;
m = The slope or the rate of change of the height with the number of flower pots in a stack which can be found from two points in the given table of values
c = The y-intercept or height at the start of the first stack
From the table of values, for the first and the last points, we have;
m = (52 - 28)/(5 - 1) = 24/4 = 6
Which gives;
h - 52 = 6×(n - 5)
h = 6·n - 30 + 52 = 6·n + 22
h = 6·n + 22
Where;
h = The height of stack in cm
n = The number of flower pots
Therefore, by comparing to the general form of the equation of a straight line, y = m·x + c, the y-intercept, c = 22
The simplified algebraic expression to represent the height of a stack of n flower pots is therefore given as h = 6·n + 22.
Use the formula for arc length to find the value of the unknown quantity.
s=rθ

Answers
The unknown quantity which is the radius has a length of 49752/π yards.
How to find arc length?The formula for the length of arc is;
S = rθ
where;
r is radius
θ is the central angle in radians
Now, we are given;
θ = 3π/4
S = 4146 * 9 yards
Thus, making r the subject and solving gives;
r = S/θ
r = (4146 * 9)/(3π/4)
r = 49752/π
Thus, the unknown quantity which is the radius has a length of 49752/π yards.
Read more about Arc Length at; https://brainly.com/question/2005046
#SPJ1
Round each z-score to the nearest hundredth. A data set has a mean of x = 212 and a standard deviation of 40. Find the z-score for each of the following. (a) x = 200 (b) x = 224 (c) x = 300 (d) x = 100
Answers
a) The data point 200 is 0.30 standard deviations below the mean of the data set.
b) The data point 224 is 0.30 standard deviations above the mean of the data set.
c) The data point 300 is 2.20 standard deviations above the mean of the data set.
d) The data point 100 is 2.80 standard deviations below the mean of the data set.
Now let's apply this formula to the given data set, which has a mean of x = 212 and a standard deviation of 40, and find the z-score for each of the following data points:
(a) x = 200
Using the formula, z = (x - μ) / σ, we get:
z = (200 - 212) / 40
z = -0.3
Rounding this z-score to the nearest hundredth, we get z = -0.30.
(b) x = 224
Using the same formula, we get:
z = (224 - 212) / 40
z = 0.3
Rounding this z-score to the nearest hundredth, we get z = 0.30.
(c) x = 300
Using the formula, we get:
z = (300 - 212) / 40
z = 2.2
Rounding this z-score to the nearest hundredth, we get z = 2.20.
(d) x = 100
Using the formula, we get:
z = (100 - 212) / 40
z = -2.8
Rounding this z-score to the nearest hundredth, we get z = -2.80.
To know more about z-score here
https://brainly.com/question/31871890
#SPJ4