The y intercept is represented by what variable in the equation y=my+b
Answers
Answer:
b
Step-by-step explanation:
Answer:
The y-intercept is represented by the variable b in this equation.
Related Questions
six thirty children had gallon of lemonade to share. if each child had the same amount, what portion of the gallon did each child have to drink?
Answers
If each child consumed the same quantity, then each would need to drink (63)x(4/n) of a gallon.
The US fluid ounce is equal to 1/128 of a US gallon since there are four quarts in a gallon, two pints in a quart, and 16 US fluid ounces in a US pint. The US gallon is accepted to be equivalent to around 3.785 L or 231 in inches, but the Imperial gallon is accepted to be equal to 4.54609 L. The liter is the unit of volume used by the great majority of people in the world. a volume measurement equal to eight pints.
An imperial gallon (Britain, Canada) is exactly 4.54609 liters. (US) 3.785 liters or around 231 cubic inches for liquids (a "U.S. liquid gallon")
Here gallon of lemonade to share = 63
let each children has 1 gallon of lemonade
so gallon=63
so portion =63/1
Formula = gallon to share x (4 parts of gallon shape / number of gallon)
which means if each one have n gallon then portion = (63)x(4/n)
Learn more about gallon Visit: brainly.com/question/28274339
#SPJ4
Each child would need to eat 63*4/n of a gallon if they all consumed the same amount.
Since there are four quarts in a gallon, two pints in a quart, and 16 US fluid ounces in a US pint, one US fluid ounce is equivalent to 1/128 of a US gallon. The Imperial gallon is acknowledged to be equal to 4.54609 L, but the US gallon is accepted to be about 3.785 L or 231 in. The vast majority of people in the world measure volume in litres. a volume that is eight pints in size.
In Britain and Canada, an imperial gallon equals precisely 4.54609 litres. 3.785 litres (US) or around 231 cubic inches (a "U.S. liquid")
Here, six thirty kids were sharing a gallon of lemonade.
each youngster should drink a gallon of lemonade.
Gallon = 63.
Hence part = 63/1
It indicates that the fraction is equal to 63*4/n if each has n gallons.
For such more question on gallon
https://brainly.com/question/28274339
#SPJ4
Note: The complete question would be as bellow,
six thirty children had gallon of lemonade to share. if each child had the same amount, what portion of the gallon did each child have to drink?
If 6J of work is needed to stretch a spring from 10 cm to 12 cm and another 10J is needed to stertch it from 12 cm to 14 cm, what is the natural length of the spring?
Answers
To solve this problem, we can use the formula for the potential energy stored in the spring:
U = 1/2 k x^2
where U is the potential energy stored in the spring, k is the spring constant, and x is the displacement of the spring from its natural length.
From the given information, we can set up two equations:
6J = 1/2 k (0.02)^2
10J = 1/2 k (0.02)^2 + 1/2 k (0.02)^2
Simplifying the equations, we get:
6J = 0.0002 k
10J = 0.0004 k
Dividing the second equation by the first, we get:
10J/6J = 0.0004 k/0.0002 k
Simplifying, we get:
5/3 = 2
This is not possible, so there must be an error in the problem. Therefore, we cannot determine the natural length of the spring with the given information.
Learn more about it here:
https://brainly.com/question/31642352
#SPJ11
Marjane wants to create a set of data with 6 values. She wants the mode to be as good as the median to represent the data set. Which set of data best represents what Marjane could create?
24, 24, 25, 29, 29, 29
24, 25, 26, 27, 30, 30
24, 25, 25, 25, 26, 26
24, 24, 25, 26, 26, 27
Answers
As per the median, the set of data that fulfilling Marjane's requirement is 24, 25, 25, 25, 26, 26 (option c).
In statistics, data is a collection of numbers or values that represent a particular phenomenon. One way to measure central tendency, or the typical or representative value of the data, is through the median and the mode.
The median is the middle value when the data is arranged in numerical order, and the mode is the value that appears most frequently.
The third set of data is 24, 25, 25, 25, 26, 26.
The median is the middle value, which is also (25+25)/2 = 25.
The mode is the value that appears most frequently, which is 25.
Therefore, the mode and median are the same, fulfilling Marjane's requirement.
Therefore, the correct option is (c).
To know more about median here
https://brainly.com/question/30891252
#SPJ4
(3X-5)^1/4+3=4
Your anwser should be x=2!
SHOW WORK
Answers
(Explanation below)
x=2

x = 2 is the solution of the equation
What is Equation?Two or more expressions with an Equal sign is called as Equation.
The given equation is \((3X-5)^(^1^/^4^) + 3 = 4\)
We have to find the value of x
Subtracting 3 from both sides:
\((3X-5)^(^1^/^4^) = 1\)
Raising both sides to the fourth power:
3X - 5 = 1^4
3X - 5 = 1
Adding 5 to both sides:
3X = 6
Dividing by 3:
X = 2
Therefore, x = 2 is the solution of the equation
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ2
PLEASE HELP!
simplify this expression
4(7x + 5y)
Answers
28x + 20y should be it.
#9Change from standard form to vertex formy= -x²+4x-1
Answers
So the vector form of the equation is: y = -1(x - 2)² + 3.
To convert from standard form to vertex form, we complete the square by following these steps:
Factor out the coefficient of the x-squared term:
y = -x² + 4x - 1
= -1(x² - 4x) - 1
To complete the square inside the parentheses, add and subtract the square of half of the coefficient of the x-term (-4/2)^2 = 4:
y = -1(x² - 4x + 4 - 4) - 1
Simplify the expression inside the parentheses by factoring a perfect square:
y = -1((x - 2)² - 4) - 1
Distribute the -1 and simplify:
y = -1(x - 2)² + 3
Therefore, the vertex of the parabola is at (2, 3), and the negative coefficient of the x-squared term means that the parabola opens downwards.
To know more about vector,
https://brainly.com/question/30202103
#SPJ11
1^2/10 as a negative power of 10
Answers
Ryan and his friends have a half-day at school, so they plan to spend the afternoon paddleboarding at Lake Evergreen. They want to spend the rest of the day on the water..

Answers
D Calculate the value of the error with one decimal place for: Z= # where x = 5.9 +/-0.5 and y = 2.1 +/- 0.2 Please enter the answer without +/- sign. 4 Question 2 Calculate the value of the error wit
Answers
The value of the error for Z, where x = 5.9 +/- 0.5 and y = 2.1 +/- 0.2, with one decimal place is 4.
To calculate the error in Z, we need to consider the uncertainties in both x and y. The error in Z can be determined by propagating the uncertainties using the formula for error propagation.
In this case, Z is given by the equation Z = x/y. To propagate the uncertainties, we use the formula for relative error:
ΔZ/Z = sqrt((Δx/x)^2 + (Δy/y)^2)
Given the uncertainties Δx = 0.5 and Δy = 0.2, and the values x = 5.9 and y = 2.1, we substitute these values into the formula:
ΔZ/Z = sqrt((0.5/5.9)^2 + (0.2/2.1)^2) = sqrt(0.0089 + 0.0181) ≈ 0.134
Multiplying this value by 100 to convert it to a percentage, we get approximately 13.4%. Rounding to one decimal place, the value of the error is 4.
Therefore, the value of the error for Z, with one decimal place, is 4.
to learn more about value click here
brainly.com/question/30760879
#SPJ11
Abdullah and Amna bought a car for $9000, Abdullah paid 45% of the $9000 and Amna paid
the rest.
b) Write down the ratio of the payments Abdullah: Amna in its simplest form.
Answers
Answer:
9 : 11
is your a nswer in it's simplest form
Step-by-step explanation:
Abdullah and Amna bought a car for $9000, Abdullah paid 45% of the $9000 and Amna paid
the rest.
b) Write down the ratio of the payments Abdullah: Amna in it's simplest form.
Abdullah paid 45% means Amna paid 55% (100% - 45% = 55%), so the Abdullah : Amna ratio is 45 : 55, let's simplify by dividing the two parts by 5 and we will have the ratio in its simplest form.
45 : 55
let's simplify
9 : 11 is your answer
Suppose the amount of a popular sport drink in bottles leaving the filling machine has approximately a normal distribution with mean 101.5 milliliters (ml) and standard deviation 1.6 ml. a. If the bottles are labeled 100 ml, what proportion of the bottles contain less than the labeled amount? b. If only 2.5% of the bottles have contents that exceed a specified amount c, what is the value of c?
Answers
About 17.45% of the bottles contain less than the labelled amount of 100 ml.
To find this proportion, we first standardize the labeled amount of 100 ml to a z-score using the formula z = (x - mu) / sigma, where x is the labelled amount, mu is the mean, and sigma is the standard deviation.
z = (100 - 101.5) / 1.6 = -0.9375
We then find the area under the standard normal distribution curve to the left of this z-score using a standard normal distribution table or calculator. This area is approximately 0.1745, which means that about 17.45% of the bottles contain less than the labeled amount of 100 ml.
The value of c is approximately 104.456 ml.
To find this value, we first need to find the z-score that corresponds to the upper 2.5% of the standard normal distribution. Using a standard normal distribution table or calculator, we find that this z-score is approximately 1.96.
We then use the same formula as before, z = (x - mu) / sigma, to solve for the corresponding value of c in milliliters.
1.96 = (c - 101.5) / 1.6
Solving for c, we get:
c = 1.96 * 1.6 + 101.5 = 104.456
Therefore, if only 2.5% of the bottles have contents that exceed a specified amount, that amount is approximately 104.456 ml.
For more similar questions on probability:
brainly.com/question/13604758
#SPJ11
a philosophy professor assigns letter grades on a test according to the following scheme. a: top 13% of scores b: scores below the top 13% and above the bottom 62% c: scores below the top 38% and above the bottom 15% d: scores below the top 85% and above the bottom 8% f: bottom 8% of scores scores on the test are normally distributed with a mean of 69.5 and a standard deviation of 9.5 . find the minimum score required for an a grade. round your answer to the nearest whole number, if necessary.
Answers
To find the minimum score required for an A grade, we need to determine the cutoff point that corresponds to the top 13% of scores.
Given that the scores on the test are normally distributed with a mean of 69.5 and a standard deviation of 9.5, we can use the standard normal distribution to calculate the cutoff point. Using a standard normal distribution table or a statistical calculator, we find that the z-score corresponding to the top 13% is approximately 1.04. To find the corresponding raw score, we can use the formula:
x = μ + (z * σ)
where x is the raw score, μ is the mean, z is the z-score, and σ is the standard deviation. Plugging in the values, we have:
x = 69.5 + (1.04 * 9.5) ≈ 79.58
Rounding this to the nearest whole number, the minimum score required for an A grade would be 80. Therefore, a student would need to score at least 80 on the test to achieve an A grade according to the professor's grading scheme.
Learn more about grade here
https://brainly.com/question/30659423
#SPJ11
What is the value of a for the exponential function in the
graph represented in the form of f(x) = a(b)?
O -4
O -3
O 3
O 4

Answers
Answer:
Option (4)
Step-by-step explanation:
If the given exponential function is in the form of f(x) = \(a(b)^x\)
From the graph we find that two points (0, 3) and (0.5, 6) lie on the graph.
For (0, 3),
f(0) = \(a(b)^0\)
3 = a
For (0.5, 6),
f(0.5) = \(3(b)^{0.5}\)
6 = \(3\sqrt{b}\)
\(\sqrt{b}=2\)
b = 4
Therefore, value of b in the given function 'f' is 4.
Option (4) will be the answer.
Answer:
(D) 4
Step-by-step explanation:
♥☺
HELP ME WITH THIS ASAP TYSM

Answers
Answer:
6 + 21r
Step-by-step explanation:
3 ( 2 + 7r )
3 ( 2 ) = 6
3 ( 7r ) = 21r
6 + 21r
Hope this helps dude ^-^
Answer: 6 + 21r
Step-by-step explanation:
distribute the 3 to each thing in the parentheses
so 3(2 + 7r) becomes
3(2) + 3(7r)
6 + 21r
Suppose that grade point averages of undergraduate students at one university have a bell-shaped distribution with a mean of 2.61 and a standard deviation of 0.45. Using the empirical rule, what percentage of the students have grade point averages that are at least 3.96?
Answers
Approximately 0.3% of the students have grade point averages that are at least 3.96.
To determine the percentage of students who have grade point averages that are at least 3.96, we can use the empirical rule (also known as the 68-95-99.7 rule) in conjunction with the given mean and standard deviation of the distribution.
The empirical rule states that for a bell-shaped (normal) distribution:
Approximately 68% of the data falls within one standard deviation of the mean.
Approximately 95% of the data falls within two standard deviations of the mean.
Approximately 99.7% of the data falls within three standard deviations of the mean.
In this case, we want to find the percentage of students who have grade point averages greater than or equal to 3.96. To do this, we need to calculate the z-score corresponding to the GPA of 3.96, and then determine the percentage of data that falls to the right of that z-score.
The z-score formula is:
z = (x - μ) / σ
Where:
x is the value we want to find the z-score for (3.96 in this case),
μ is the mean (2.61),
σ is the standard deviation (0.45).
Calculating the z-score for 3.96:
z = (3.96 - 2.61) / 0.45 ≈ 2.99
Now, let's interpret the z-score:
A z-score of 2.99 indicates that the GPA of 3.96 is approximately 2.99 standard deviations above the mean.
Using the empirical rule, we know that approximately 99.7% of the data falls within three standard deviations of the mean. Since 3.96 is more than three standard deviations above the mean, the percentage of students with GPAs at least 3.96 can be estimated as the percentage of data beyond three standard deviations.
Considering the right tail of the distribution, we can estimate the percentage using the complement of the percentage within three standard deviations. Thus, the percentage of students with GPAs at least 3.96 is approximately:
100% - 99.7% = 0.3%
for such more question on percentage
https://brainly.com/question/24877689
#SPJ8
The percentage of students with grade point averages that are at least 3.96 is approximately 0.3%.
Give that:
The value o 3.96,
The mean: μ = 2.61,
Standard deviation: σ = 0.45.
To use the empirical rule, to assume that the grade point averages follow a normal distribution.
The empirical rule, also known as the 68-95-99.7 rule, provides approximate percentages of data within certain standard deviations from the mean in a normal distribution.
According to the empirical rule:
Approximately 68% of the data falls within one standard deviation of the mean.
Approximately 95% of the data falls within two standard deviations of the mean.
Approximately 99.7% of the data falls within three standard deviations of the mean.
To find the percentage of students with grade point averages that are at least 3.96, which means to find the percentage of data that falls above this value.
Step 1: Calculate the z-score for 3.96:
Z = (X - μ) / σ
Z = (3.96 - 2.61) / 0.45 ≈ 2.98
Step 2: Find the percentage of data that falls beyond this z-score. Since we are looking for values greater than 3.96, we look at the percentage beyond 2.98 (which is approximately three standard deviations above the mean).
According to the empirical rule, approximately 99.7% of the data falls within three standard deviations of the mean. This means that approximately 100% - 99.7% = 0.3% of the data falls beyond three standard deviations from the mean.
So, the percentage of students with grade point averages that are at least 3.96 is approximately 0.3%.
Learn more about Empirical rule here:
https://brainly.com/question/30573266
#SPJ4
Answer: The domain for f(x) is all real numbers GREATER than equal to 3
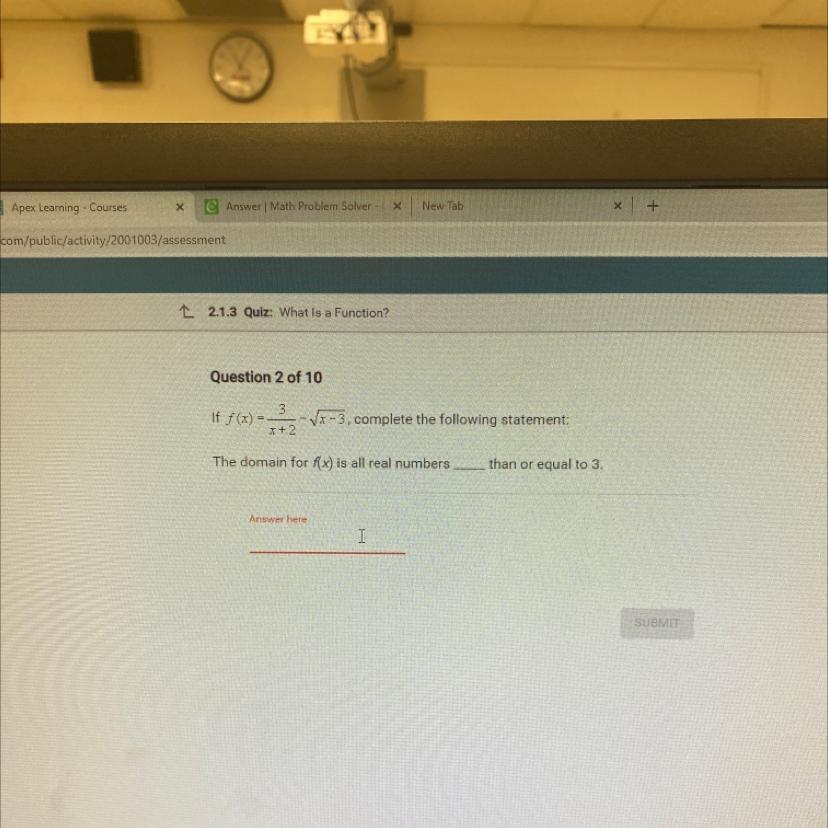
Answers
Answer:A≈1075.21
d Diameter
37
d
r
r
r
d
d
C
A
Using the formulas
A=
π
r
2
d=
2
r
Solving forA
A=
1
4
π
d
2
=
1
4
π
37
2
≈
1075.21009
Step-by-step explanation:
SOMEONE DO NUMBER 1 AND 2 FOR ME, ILL GIVE BRAINLIEST

Answers
Answer:
1. The second number line, the third number line, the first number line.
2.
\(a) \: 1 \frac{7}{8} > \frac{7}{4} \)
\(b) \: \frac{21}{5} = 4 \frac{1}{5} \)
\(c) \frac{13}{4} < 3 \frac{5}{6} \)
9000km to m = 15,000 m to km80mm to dm
Answers
For every 1 km = there are 1,000 meters. Therefore:
\(9,000\operatorname{km}\times\frac{1,000m}{1\operatorname{km}}=9,000,000m\)15,000 m to km is:
\(15,000m\times\frac{1\operatorname{km}}{1,000m}=\frac{15000}{1000}=15\operatorname{km}\)For every 1 decimeter, there are 100 millimeters.
\(80\operatorname{mm}\times\frac{1dm}{100\operatorname{mm}}=\frac{80}{100}=0.8dm\)Hi thank you so for all your time and help

Answers
Hello there. To solve this question, we'll have to remember some properties about trigonometric functions and the right triangle.
We want to find x such that:
\(\tan (x)=\sqrt[]{3}\)We'll use the second right triangle to show what we want.
First, given a triangle:
We know that the hypotenuse will be:
\(\sqrt[]{x^2+y^2}\)But most importantly, the tangent of the angles α and β can be calculated by only using the legs of the triangle: it is the ratio between the opposite side and the adjacent side to an angle.
\(\tan (\alpha)=\frac{y}{x}\)and
\(\tan (\beta)=\frac{x}{y}\)Now look at the triangle we have:
We can easily check that:
\(\sqrt[]{3}=\frac{\sqrt[]{3}}{1}\)So it would be good to find something that relates the ratio between those two numbers: the tangent of 60º!!
Therefore, we have:
\(\tan (60^{\circ})=\frac{\sqrt[]{3}}{1}=\sqrt[]{3}\)And the solution to x is:
\(x=60^{\circ}\)

PLEASE HELP ASAP
I'LL MARK BRAINIEST

Answers
Answer:
x = 1.24628
hope it helps
what is the probability that the first person who subscribes to the five second rule is the 5th person you talk to
Answers
The probability that the first person who subscribes to the five-second rule is the 5th person you talk to is q⁴ * p.
To calculate the probability that the first person who subscribes to the five-second rule is the 5th person you talk to, we need to consider the following terms: probability, independent events, and complementary events.
Step 1: Determine the probability of a single event.
Let's assume the probability of a person subscribing to the five-second rule is p, and the probability of a person not subscribing to the five-second rule is q. Since these are complementary events, p + q = 1.
Step 2: Consider the first four people not subscribing to the rule.
Since we want the 5th person to be the first one subscribing to the rule, the first four people must not subscribe to it. The probability of this happening is q * q * q * q, or q⁴.
Step 3: Calculate the probability of the 5th person subscribing to the rule.
Now, we need to multiply the probability of the first four people not subscribing (q^4) by the probability of the 5th person subscribing (p).
The probability that the first person who subscribes to the five-second rule is the 5th person you talk to is q⁴ * p.
To learn more about Probability
https://brainly.com/question/24870672
#SPJ11
what is the output of the following code snippet? public static void main(string[] args) { int value = 3; value ; system.out.println(value); }
Answers
The output obtained after executing the java code snippet,
public static void main(string[] args)
{
int value = 3;
value++;
system.out.println(value);
}
will be 4.
As per the question statement, we are provided with a java code snippet, which goes as:
public static void main(string[] args)
{
int value = 3;
value++;
system.out.println(value);
}
We are required to determine the output, that we will obtain on executing the above mentioned code.
That is, on executing the code
public static void main(string[] args)
{
int value = 3;
value++;
system.out.println(value);
}
We will obtain an output of 4, as "++" is the post increment function.
Java: Java is a general-purpose, class-based, object-oriented programming language designed for having lesser implementation dependencies, where all programs are made of entities representing concepts or physical things known as “objects”Output: Output is the result of any action.To learn more about Java Code snippets and their Outputs, click on the link below
https://brainly.com/question/28400793
#SPJ4
Yolanda is 4 years younger than 3 times her daughter's age. The sum of their ages is greater than 88. What is the youngest age Yolanda's daughter can be?
Answers
Answer: The youngest age yolanda's daughter can be is 24 years old.
The youngest age of Yolanda's daughter is 23 years if Yolanda is 4 years younger than 3 times her daughter's age. The sum of their ages is greater than 88.
What is a linear equation?It is defined as the relation between two variables, if we plot the graph of the linear equation we will get a straight line.
If in the linear equation, one variable is present, then the equation is known as the linear equation in one variable.
It is given that:
Yolanda is 4 years younger than 3 times her daughter's age. The sum of their ages is greater than 88.
Let the age of Yolanda's is y and
The age of the Daughters is x
From the data given we can frame two linear equations in two variables as follows:
y = 3x - 4
x + y = 88
After solving the above two equations using the substitution method:
x + (3x-4) = 88
x + 3x - 4 = 88
4x = 92
x = 92/4
x = 23
y = 88 - 23 = 65
Thus, the youngest age of Yolanda's daughter is 23 years if Yolanda is 4 years younger than 3 times her daughter's age. The sum of their ages is greater than 88.
Learn more about the linear equation here:
brainly.com/question/11897796
#SPJ2
PLEASEEEE SOMEONE HELP I GIVE AS MUCH POINTS :’( Thank you!

Answers
The approximate area of the trapezoid is determined as 13.95 unit².
What is the approximate area of the trapezoid?The approximate area of the trapezoid is calculated as follows;
Area = ¹/₂(b₁ + b₂)h
Where;
b₁ and b₂ are the lengths of the parallel sidesh is the heightThe y-coordinates of the points on the curve at x=3/2 and x=4 is calculated as follows;
y(3/2) = - (3/2)²/2 + 3/2 + 5
y(3/2) = -9/8 + 3/2 + 5
y(3/2) = 5.375
y(4) = -4²/2 + 4 + 5
y(4) = -8 + 9
y(4) = 1
h = 5.375 - 1 = 4.375
The approximate area of the trapezoid is calculated as;
Area = ¹/₂(5.375 + 1) x 4.375
Area = 13.95 unit²
Learn more about approximate area of trapezoid here: https://brainly.com/question/22357828
#SPJ1
1/sinx+cosx + 1/sinx-cosx = 2sinx/sin^4x-cos^4x
Answers
The simplified expression is 2cos²(x) + sinx - 1 = 0
The expression we will be simplifying is
=> 1/sinx+cosx + 1/sinx-cosx = 2sinx/sin⁴x-cos⁴x.
To begin, let us look at the left-hand side of the expression. We can combine the two fractions using a common denominator, which gives us:
(1/sinx+cosx)(sinx-cosx)/(sinx+cosx)(sinx-cosx) + (1/sinx-cosx)(sinx+cosx)/(sinx-cosx)(sinx+cosx)
Simplifying this expression using the distributive property, we get:
(1 - cosx/sinx)/(sin²ˣ - cos²ˣ) + (1 + cosx/sinx)/(sin²ˣ - cos²ˣ)
Next, we can simplify each fraction separately. For the first fraction, we can use the identity sin²ˣ - cos²ˣ = sinx+cosx x sinx-cosx to obtain:
1 - cosx/sinx = (sinx+cosx - cosx)/sinx = sinx/sinx = 1
Similarly, for the second fraction, we can use the same identity to obtain:
1 + cosx/sinx = (sinx-cosx + cosx)/sinx = sinx/sinx = 1
Substituting these values back into the original expression, we get:
1 + 1 = 2sinx/(sin⁴x - cos⁴x)
Now, we can simplify the denominator using the identity sin²ˣ + cos²ˣ = 1 and the difference of squares formula:
sin⁴x - cos⁴x = (sin²ˣ)² - (cos²ˣ)² = (sin²ˣ + cos²ˣ)(sin²ˣ - cos²ˣ) = sin²ˣ - cos²ˣ
Substituting this back into the expression, we get:
2 = 2sinx/(sin²ˣ - cos²ˣ)
Finally, we can simplify the denominator using the identity sin²ˣ - cos²ˣ = -cos(2x):
2 = -2sinx/cos(2x)
Multiplying both sides by -cos(2x), we get:
-2cos(2x) = 2sinx
Dividing both sides by 2, we get:
-cos(2x) = sinx
Using the double-angle formula for cosine, we get:
-2cos²(x) + 1 = sinx
Simplifying this expression, we get:
2cos²(x) + sinx - 1 = 0
To know more about expression here
https://brainly.com/question/14083225
#SPJ4
2 – 3х + 5х = 16 — 8х + 8x
Answers
Answer:
2 – 3х + 5х = 16 — 8х + 8x
2 - 8x = 16
8x = 14,
x = 1.75
=>2-3x+5x=16-8x+8x
=>2+2x= 16
=> 2x= 16-2
=> 2x= 14
=> x=7
Aj has dollers in her account she spends $35. 31 if the balance in her account is $161. 23 what was the amount in her account before her purchase
Answers
A line with a slope of 1/5 through the point (3,-6). What is its equation in point slope form
Answers

The diameter of a quarter is about 1
in.
You trace around the edge of the quarter on a sheet of paper.
What is the area of the circle on the paper?
Use 3.14
as an approximation for π
. Round your answer to the nearest tenth.
Answers
The area of the circle which is drawn by tracing around the edge of the quarter on a sheet of paper is 0.78 in.²
What is meant by a quarter of a circle?All points in a plane that are at a specific distance from a specific point, the centre, form a circle. In other words, it is the curve that a moving point in a plane draws to keep its distance from a specific point constant.
Each of the four equally sized pieces that make up a circle is known as a quarter of a circle. The quadrant of the circle is the name given to each quarter. One-fourth of the total area of the circle is represented by the area of a quarter circle.
Given,
the diameter of the quarter = 1 in.
When we trace around the edge of the quarter on a sheet of paper, we get a circle of diameter 1 in.
So the radius of the circle r = 1/2 = 0.5 inches
Area of the circle on the paper = πr² = 3.14 × 0.5² = 0.78 in.²
Therefore the area of the circle which is drawn by tracing around the edge of the quarter on a sheet of paper is 0.78 in.²
To learn more about the quarter, follow the link.
https://brainly.com/question/28982779
#SPJ1
Which is the best summary of this part of the passage?
A. Catherine patented an invention that lets patients track their own heartbeats
B. Catherine patented an invention that lets patients talk to doctors on a cell phone
C. Catherine patented an invention that lets doctors operate on a patient's heart and lungs
D. Catherine patented an invention that lets doctors hear a patient's heart and lungs
Answers
Answer: d
hahehebbsjdhdbrbsndjjd
Step-by-step explanation: