The volume of a cube related to the area of a face by the formula V =A^3/2. What is the volume of a cube whose face has an area of 25mm^2.

Answers
Answer:
Volume = 125 mm^3
Step-by-step explanation:
Here, we want to get the volume of the cube
What we have to do here is to substitute the value of the area
We have this as
:
V = 25^(3/2)
V = (√25)^3
V = 5 * 5 * 5 = 125 mm^3
Related Questions
1 1/2 ÷ (1 1/4 * 1 1/4) ÷ 1 2/3 ÷ (1 1/5 * 1 1/5)
Answers
Answer:
0.4
Step-by-step explanation:
Answer:
0.4
Step-by-step explanation:
What should the relative size of our samples be from each school if we want the two sampling distributions to have approximately the same standard deviation
Answers
Based on the information given, the relative size of our samples is D. We should take the same size sample from each school.
What is sampling?It should be noted that sampling simply means the selection of a subset of individuals from a population to estimate the population characteristics.
From the complete question, the relative size of our samples from each school if we want the two sampling distributions to have approximately the same standard deviation will be that we should take the same size sample from each school.
Learn more about sampling on:
https://brainly.com/question/17831271
nEED HELP please AASAP

Answers
Answer:
A = (4π/3 -√3) m^2
Step-by-step explanation:
The area of a sector with a given radius and arc measure is given by ...
A = (1/2)r^2(θ -sin(θ))
Filling in the given values, the area is ...
A = (1/2)(2 m)^2(2π/3 -sin(2π/3)) = 2(2π/3 -√3/2) m^2
A = (4π/3 -√3) m^2 . . . . . matches choice A
need asap
..............................

Answers
Answer:
\(x = 15\)Step-by-step explanation:
To find:-
The value of x.Answer:-
From the given figure we can see that there are three right angled triangles namely ∆ACB , ∆BCD and ∆ACD .
To find out the value of x , we will have to use Pythagoras theorem . The Pythagoras theorem is ,
Pythagoras theorem:-
In a right angled triangle , the sum of squares of base and perpendicular is equal to the square of hypotenuse.In a triangle hypotenuse is the longest side . In a right angled triangles, the side opposite to 90° will be hypotenuse.
Using Pythagoras theorem in ∆ACB :-
\(\longrightarrow AB^2+BC^2= AC^2 \\\)
\(\longrightarrow 9^2 + x^2 = AC^2 \dots(1)\\\)
Using Pythagoras theorem in ∆BCD:-
\(\longrightarrow BC^2 + BD^2 = CD^2 \\\)
\(\longrightarrow x^2+25^2 = CD^2 \dots(2) \\\)
Using Pythagoras theorem in ∆ACD :-
\(\longrightarrow AC^2 + CD^2 = AD^2 \\\)
Substituting the respective values from equations (1) and (2) ,
\(\longrightarrow 9^2 + x^2 + x^2 + 25^2 = (9+25)^2 \\\)
\(\longrightarrow 81 + 2x^2 + 625 = 34^2 \\\)
\(\longrightarrow 2x^2 + 706 = 1156 \\\)
\(\longrightarrow 2x^2 = 1156-706 \\\)
\(\longrightarrow 2x^2 = 450\\\)
\(\longrightarrow x^2 =\dfrac{450}{2}\\\)
\(\longrightarrow x = \sqrt{225} \\\)
\(\longrightarrow \underline{\boxed{\boldsymbol{ x = 15 }}} \\\)
Therefore the value of x is 15 .

Answer:
x = 15
Step-by-step explanation:
To find the value of x, use the Geometric Mean Theorem (Altitude Rule).
Geometric Mean Theorem (Altitude Rule)The altitude drawn from the vertex of the right angle perpendicular to the hypotenuse separates the hypotenuse into two segments. The ratio of the altitude to one segment is equal to the ratio of the other segment to the altitude:
\(\boxed{\sf \dfrac{Altitude}{Segment\:1}=\dfrac{Segment\:2}{Altitude}}\)
From inspection of the given right triangle:
Altitude = xSegment 1 = 9Segment 2 = 25To find the value of x, substitute the values into the formula and solve for x:
\(\implies \dfrac{x}{9}=\dfrac{25}{x}\)
\(\implies \dfrac{x}{9}\cdot 9x=\dfrac{25}{x}\cdot 9x\)
\(\implies x \cdot x=25\cdot9\)
\(\implies x^2=225\)
\(\implies \sqrt{x^2}=\sqrt{225}\)
\(\implies x=15\)
Therefore, the value of x is 15.
Maggie buys a dress and a pair of shoes at The Home Store. Before adding the sales tax, she pays $48 for a dress that normally sells for $62 and she pays $34 for a pair of shoes that normally sells for $46. a) Before the sales tax, how much does Maggie save on her purchases by buying at the sale price? Show all work. b) To the nearest percent, what percent discount did Maggie get on her total purchase? Show all work. c) Including a 15% sales tax, what total amount will Maggie pay?
Answers
Answer:
a) $26
b) 24.07%
c) $94.3
Step-by-step explanation:
Given that:
Before tax:
Normal price of dress = $62
Discounted price of dress = $48
Normal price of a pair of shoes = $46
Discounted price of a pair of shoes = $34
a) Before the sales tax, total savings = ($64 - $48) + ($46 - $34) = $26
b) Total percentage discount on total sales.
Total bill for original price = $62 + $46 = $108
Percentage discount can be found by the formula:
\(\dfrac{\text{Total discount}}{\text{Total bill for original price}}\times 100\\\Rightarrow \dfrac{26}{108} \times 100 = 24.07\%\)
c) Total amount paid if the sales tax is 15%.
Amount paid with tax = Amount after discount + 15% of amount after discount
Amount after discount = $48 + $34 = $82
15% of $82 = $18.29
Amount paid with sales tax = $82 + $12.3 = $94.3
EMERGENCY HELP NEEDED!!!!! 20 POINTS!!! WILL MARK BRAINLIEST!!!
A regular polygon has the same number of lines of symmetry as the number of sides. For example, a pentagon has 5 sides and 5 lines of symmetry. The number of degrees apart each line of symmetry is equals 360 degrees divided by the number of sides. The pentagon's lines of symmetry are 360/5 degrees apart, or 72 degrees apart. How many degrees apart are the triangle's lines of symmetry?
60 degrees
180 degrees
90 degrees
120 degrees
Answers
Work Shown:
360/n = 360/3 = 120
Answer:
120 degrees
Step-by-step explanation:
A triangle has Three sides, so according to the given information, it should also have three lines of symmetry. To calculate the degrees apart each line of symmetry is in a triangle, we can use the same formula
Degrees apart = 360 degrees / number of sides
For a triangle:
Degrees apart= 360 degrees / 3 sides
Therefore, the lines of symmetry in a triangle are 120 degrees apart
These dot plots show the weights (in kilograms) from a sample of leopards
and tigers.
Leopards
000
0000+
000000
00018
00
20
40
60
80
160
180
200
220
100 120 140
Weight (kg)
Tigers
000
2000
000000
2000
ooe
O
20
40
60
80
160
180
200
220
100 120 140
Weight (kg)
What are the differences between the centers and spreads of these
distributions?
Select two choices: one for the centers and one for the spreads.
No
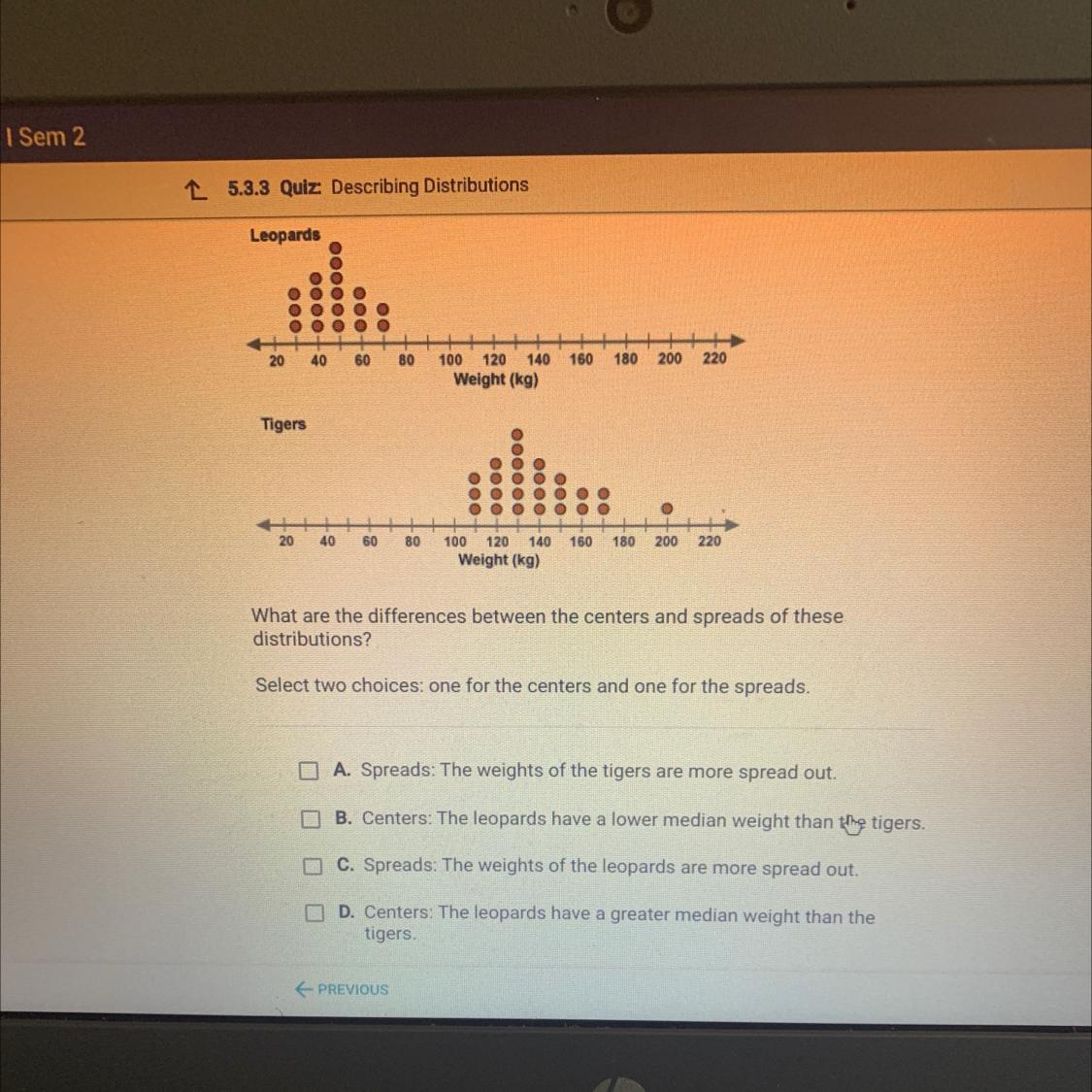
Answers
Answer: A.Spreads: The weights of the tigers are more spread out.
B.Centers:The leopards have a lower median weight than the tigers
Step-by-step explanation:
On analyzing the dot plots, we find that the weight of Leopards are more spread out and the weight of Leopards has a lower median than Tiger.
What is median?Median is a statistical measure that determines the middle value of a dataset listed in ascending order. The measure divides the lower half from the higher half of the dataset.
Median of Weight of Leopard = 50 kg
Median of Weight of Tiger = 125 kg
This implies that the Leopards have a lower median weight than Tigers.
What is spread of data?
Spread describes the variation of the data. One of the measures of spread is range.
Range of weight of Leopards= 40 kg
Range of weight of Tigers = 90 kg
This implies that the weight of Tigers are more spread out.
Learn more about median here
brainly.com/question/21396105
#SPJ2
Solve the following equation
3(1-3x)=2(-4+7)
Answers
Answer:
x=-1/3
Step-by-step explanation:
3(1-3x)=2(-4+7)
Use distributive property.
3-9x=-8+14
Combine like terms.
3-9x=6
Subtract 3 from both sides.
-9x=3
Divide -9 from both sides.
x=-1/3
Hope this helps!
Please mark as brainliest if correct!
Answer:
The value of x is -1/3.
Step-by-step explanation:
Given equation,
→ 3(1 - 3x) = 2(-4 + 7)
Now the value of x will be,
→ 3(1 - 3x) = 2(-4 + 7)
→ 3 - 9x = 2 × 3
→ -9x = 6 - 3
→ x = 3/(-9)
→ [ x = -1/3 ]
Hence, the value of x is -1/3.
You deposit some money in an account with an interest rate of 4% for 6 years. If you earned $407.83 in interest, how much did you invest? Round to
the nearest cent.
Answers
Answer:
$1,699.29
Step-by-step explanation:
A 4500 square foot roll of plastic wrap costs $23.95. If 120 square feet is need for a party game, what is the monetary value of that 120 square foot piece of plastic wrap? Round to the nearest cent.
Answers
$0.64 is the monetary value.
We are given that a 4500 square foot roll of plastic wrap costs $23.95 and we are to determine the monetary value of a 120 square foot piece of plastic wrap.
Let us find the cost per square foot by dividing the total cost of the roll by the number of square feet in the roll:
$23.95/4500 = $0.005322 per square foot
Now, we can multiply the cost per square foot by the number of square feet needed for the party game (120) to find the monetary value of the piece of plastic wrap.
Therefore, the monetary value of that 120-square-foot piece of plastic wrap is:
$0.005322 x 120 = $0.64 (rounded to the nearest cent)
Hence, the monetary value of that 120-square-foot piece of plastic wrap is $0.64.
Learn more about area:
https://brainly.com/question/28948613
#SPJ11
What is angle M in degrees?

Answers
A=82
B= 104
C= 121. (same as L)
Total for 3 angles = 307
Total for figure =360
360-307= 53
D= 53
So M=53 degrees
If k is a negative integer, which of these is DEFINITELY NEGATIVE? A. k* (k-1) * (k - 2) B. k* (k+1) C. k* (-50) D. (50-k)
Answers
Answer:
only A ans bellow
Step-by-step explanation:
let k= -4
A. k * (k - 1) * ( k - 2)
= -4 * (-4 -1) * ( -4 -2)
= -4* (-5) * (-6)
= 20*-6
= -120
B. k * ( k+1)
= -4 * ( -4+1)
= -4 * (-3)
= + 12
C. k * (-50)
= -4 * (-50)
= + 200
D . (50 - k)
= 50 - (-4)
= 50 + 4
= + 54
Mark me the brainliest
if k is negative then k(k-1)(k - 2) will be definitely negative.
What is Number system?A number system is defined as a system of writing to express numbers.
Given that k is a negative integer.
We need to find which of the given options are defnitely negative.
Let us consider k as -3.
k(k-1)(k - 2)
-3(-3-1)(-3-2)
-3(-4)(-5)=-60
Which is negative.
k(k+1)=-3(-3+1)=6 +ve
k (-50)=-3(-50)=150 +ve
(50-k)=50-(-3)=53 +ve.
Hence, if k is negative then k(k-1)(k - 2) will be definitely negative.
To learn more on Number system click:
https://brainly.com/question/22046046
#SPJ2
Evaluate each algebraic expression.
3w + 4 ; w = 1/4, 7, -2
Answers
Hope it helps, let me know if you have questions!:

let Xk be independent and normally distributed with common mean 22 and standard deviation 11 (so their common variance is 1.1.) compute (to at least four decimal places) p(−[infinity]≤∑k=181xk≤172.89)
Answers
Let Xk be independent and normally distributed with common mean 22 and standard deviation 11 (so their common variance is 1.1.). The value of p(-[infinity] ≤ ∑k=181 Xk ≤ 172.89) ≈ 0.0265.
The common variance of independent and normally distributed random variables with a common mean can be computed with the formula
σ² = Var[Xk]
= 1.1.
This can be solved by finding the standard deviation, which is equal to the square root of the variance as
σ = sqrt(1.1)
= 1.0488.
The sum of the independent and identically distributed normal random variables can be expressed as a normal random variable with a mean equal to the sum of the individual means and a variance equal to the sum of the individual variances.
Thus, we can express this random variable as ∑k=181 Xk ~ N(22 * 181, 1.1 * 181).
To solve the given problem, we need to compute the probability that the sum of the random variables lies between -infinity and 172.89.
Since the sum of normal random variables follows the normal distribution, we can standardize the sum by subtracting the mean and dividing by the standard deviation.
Let Z be the standardized random variable.
Then Z = (X - μ)/σ
Z = (∑k=181 Xk - μ)/σ, where μ = 22 * 181 and σ = sqrt(1.1 * 181).
We need to compute P(-infinity ≤ Z ≤ (172.89 - μ)/σ) = P(Z ≤ (172.89 - μ)/σ) .
Since the standard normal distribution is symmetric about zero.
This can be solved using standard normal tables or a calculator to obtain P(Z ≤ -1.9309) ≈ 0.0265 (rounded to four decimal places).
Therefore, p(-[infinity] ≤ ∑k=181 Xk ≤ 172.89) ≈ 0.0265 (rounded to four decimal places).
To know more about standard deviation, visit:
https://brainly.com/question/29115611
#SPJ11
Find the measure of angle A.
A
7x-1
12x
489

Answers
Answer:
48 degrees
Step-by-step explanation:
7X-1+12x+48=180
19x+47=180
19x=133
x=7
7(7)-1=A
49-1=A
48=A
A is 48 degrees
A normal population has a mean of $75 and standard deviation of $5. You select random samples of 40. a Apply the central limit theorem to describe the sampling distribution of the sample mean with » = 40. What condition is necessary to apply the central limit theorem?
Answers
The Central Limit Theorem states that for a random sample of n observations drawn from any population with a finite mean μ and a finite standard deviation σ, the sampling distribution of the sample mean approaches a normal distribution as the sample size increases, regardless of the shape of the population distribution.
To apply the Central Limit Theorem, the following condition is necessary:
1. The random sample should be selected from a population that has a finite mean (μ) and a finite standard deviation (σ).
In this case, the population mean is given as $75 and the population standard deviation is given as $5. Since both the mean and standard deviation are finite, the condition for applying the Central Limit Theorem is satisfied.
To know more about Limit visit:
brainly.com/question/12211820
#SPJ11
Answer the photo below thanks

Answers
17 x 3.4 = 53.38
53.38 Rounded Down Is 53
I need help I’m not totally understand what to do

Answers
Answer:
c ------ 1/3(40) ft^3
Step-by-step explanation:
searched the formula for volume of a cylinder
Triangle SAM is congruent to Triangle REN. Find x and y.

Answers
\(\measuredangle A\cong \measuredangle E\implies 112=16x\implies \cfrac{112}{16}=x\implies \boxed{7=x} \\\\[-0.35em] ~\dotfill\\\\ \overline{MS}\cong \overline{NR}\implies 41=3x+5y\implies 41=3(7)+5y\implies 41=21+5y \\\\\\ 20=5y\implies \cfrac{20}{5}=y\implies \boxed{4=y}\)
1) The distance between two points on a map is 6.5 cm. The scale of the map is 1:1000. Find the actual distance between the two points in km.
I need the answer asap
Answers
Answer:
0.065
Step-by-step explanation:
Scale = 1:1000
1 cm ⇒ 1000 cm = 10*100 cm = 10 m= 0.01 km6.5 cm ⇒ 0.01*6.5 km = 0.065 kmActual distance is 0.065 km
When it is 4:00 a. M. In Halifax, it is 1:00 p. M. In Karachi, and when it is 9:00 a. M. In Karachi, it is 5:00 a. M. In Warsaw. Mary left Halifax to fly to Karachi, but she accidentally left her watch on Warsaw time. According to Mary’s watch, she left Halifax at 9:40 p. M. On Monday. The local time when she arrived at Karachi was 3:00 p. M. Tuesday. How long was Mary’s flight? a. 9 hours, 20 minutes b. 13 hours, 20 minutes c. 14 hours, 20 minutes d. 17 hours, 20 minutes.
Answers
Answer:
i dont
Step-by-step explanation:
thanks for points thoo
In the accompanying diagram of triangle ABC , D is a point on AC , AB is extended to E, and DE is drawn so that triangle ADE~ triangle ABC . If m

Answers
Answer:
m∡ADE = 80°
Step-by-step explanation:
m∡ADE = m∡ABC
m∡B = 180-(30+70) = 80°
therefore, m∡ABC = 80° and so does m∡ADE because they are congruent
Find the slope of the line passing through the points (5, -8) and (3, -4).
Answers
Answer:
Slope = -2
Step-by-step explanation:
Hope this helps! Pls give brainliest!
Answer:
-2
Step-by-step explanation:
The cost of 8 identical books cost £36 what is the cost of 12 of these books?
Answers
Let fx) = x + 11 + 2 and g(x) - 2 x + 11. When does f(x) = g(x)?
Answers
Answer:when x= -2/3
That means, when the common product of f(x) & g(x) is x+2/3
Step-by-step explanation:
Find the solution set of 3x + 11 < 50 using inverse operations and properties of inequality.
Answers
Answer:
the answer is 13
Step-by-step explanation:
x < 13 that's what the answer is
Answer: (-♾️ 13)
Step-by-step explanation:
3x+11<50
3x<50-11
3x<39
X<13
The solution will be (-♾️ 13)
Simon designed the game below, which is played by throwing darts onto the board. A dartboard. From smallest to largest, the circles are labeled 20, 15, 10, 5. If Simon throws one dart, which probability would be most likely? Simon earns 10 or more points. Simon earns 15 or more points. Simon earns exactly 10 points. Simon earns exactly 15 points.
Answers
Answer:
A
Step-by-step explanation:
Simon will mostly make more than ten points, so do A
Answer:
a
Step-by-step explanation:
What is the solution to 5(x-1)+3x=7(x+1)
Answers
Answer: x = 12
Step-by-step explanation:
5(x-1)+3x=7(x+1)
5x - 5 + 3x = 7x + 7
8x - 5 = 7x + 7
x - 5 = 7
x = 12
Which is the correct formula to calculate the volume of a cone? a. Four-thirds pi r squared c. One-third pi r cubed b. One-third pi r squared h d. 4 pi r cubed
Answers
Answer:
One-third pi r squared h
Step-by-step explanation:
Answer:
B.
Step-by-step explanation:
Charlotte and Layla are workers in a factory making widgets. Layla can make 20
widgets per day in the factory. Charlotte is able to produce 10% fewer widgets per day
than Layla. How many widgets can Charlotte make per day?