The vertices of ∆CDE are C(–3, 3), D(4, 9), and E(6, 1). Translateusing ∆CDE vector (5,-3)
Answers
Answer:
The answer is D(4, 9)
Step-by-step explanation:
Related Questions
\angle a∠aangle, a and \angle b∠bangle, b are complementary angles. \angle a∠aangle, a measures 22^\circ22
∘
22, degrees.
What is the measure of \angle b∠bangle, b?
Answers
Answer:
68 degrees
Step-by-step
22 degrees +B=90 degrees
B=68
What is the base (in inches) of a triangle with an area of 161 square inches and a height of 14 inches?
Answers
\(\textit{area of a triangle}\\\\ A=\cfrac{1}{2}bh ~~ \begin{cases} b=base\\ h=height\\[-0.5em] \hrulefill\\ h=14\\ A=161 \end{cases}\implies 161=\cfrac{1}{2}b(14) \\\\\\ 161=7b\implies \cfrac{161}{7}=b\implies 23=b\)
Graph from slope-intercept form Graph y=(3)/(4)x+2
Answers
Answer:
Step-by-step explanation:
y = (3/4) x +2 is a line so find 2 points and draw a line trough them
one point is the y-intercept ( 0, 2) because y=mx+b and b is the y-intercept
second point you can find using the slope m=3/4 so from (0, 2) you will get to ( 0+4, 2+3) so your second point is (4, 5)
to graph draw a line trough (0, 2) and (4, 5)
when the stretched string of the apparatus represented below is made to vibrate, point p does not move. point p is most probably at the location of
Answers
A node is a point of no displacement in a standing wave. Therefore, if point P does not move, it is most likely located at a node. the points along the wave that experience maximum displacement are called antinodes.
A node is a point of no displacement in a standing wave, meaning that if the stretched string of the apparatus represented is made to vibrate, point P will not move. Point P is most likely located at a node as it experiences no displacement. A standing wave is created when two waves combine and the resulting wave is stationary. The points along the wave that experience no displacement are called nodes, and the points along the wave that experience maximum displacement are called antinodes. Nodes can be found at points that are integral multiples of half the wavelength of the wave. Therefore, it can be concluded that point P is at a node since it does not move when the string is made to vibrate.
The complete question is :
When the stretched string of the apparatus represented below is made to vibrate, point p does not move. Point p is most probably at the location of _____.
Learn more about maximum here
https://brainly.com/question/29156925
#SPJ4
Giving out the 15 points help please number 2.

Answers
Answer:
B that's the answer for that
Cómo resolver con cambio de variable

Answers
The solution of the integral by variable change is equal to (1 / 6) · √(2 · x + 3)³ - (3 / 2) · √(2 · x + 3).
How to solve an integral by variable change
In this problem we find the definition of an integral, whose solution must be found by variable change, that is, a kind of algebraic substitution. First, write the complete expression:
∫ [x / √(2 · x + 3)] dx
Second, use algebraic substitution to simplify the expression:
u = 2 · x + 3
x = (u - 3) / 2
dx = du / 2
(1 / 2) ∫ [(u - 3) / (2 · √u)] du
(1 / 4) ∫ [(u - 3) / √u] du
(1 / 4) ∫√u du - (3 / 4) ∫ du / √u
Third, solve the integral:
(1 / 6) · √u³ - (3 / 2) · √u
Fourth, revert the algebraic substitution:
(1 / 6) · √(2 · x + 3)³ - (3 / 2) · √(2 · x + 3)
To learn more on indefinite integrals: https://brainly.com/question/28036871
#SPJ1
How do i find out how to state the restrictions if there is any

Answers
We have the expression:
\(x=\frac{3}{4}+\frac{5}{4}\rightarrow x=\frac{8}{4}\rightarrow x=2\)So, x=2 and we dont have any restriction.
A normal distribution of scores has a standard deviation of 182.56 and a mean of 265.95. Find the z-score of 235.90.
Answers
The z-score of 235.90, if a normal distribution of scores has a standard deviation of 182.56 and a mean of 265.95, is -0.165.
What is mean?The mean of the set of data is equal to the sum of all the quantities in the data, and divide by the no of quantities.
Given:
The standard deviation, d = 182.56,
The mean, m = 265.95,
The observation value, X = 235.90
Calculate the z score by the following formula given below,
Z = (X - m) / d,
Here, Z is the Z score,
Z = 235.90 - 265.95 / 182.56
Z = -0.165
Therefore, the z-score of 235.90, if a normal distribution of scores has a standard deviation of 182.56 and a mean of 265.95, is -0.165.
To know more about mean:
https://brainly.com/question/28108712
#SPJ1
WILL GIVE BRAINLEST
PLS HELP...

Answers
Answer: what yo grade
Step-by-step explanation:
There are 9 girls and 10 boys taking dance lessons. Write the ratio that compares the number of girls taking dance lessons to the total number of students taking dance lessons.
Answers
Hey there!
9:19
This is because there are 19 total people taking dance lessons - 9 + 10 - and there are 9 girls taking dance lessons, so the ratio is girls to total students, or 9:19
Hope it helps and have a great day!
What is the slope: (-2, 1) (5,-2)
Answers
Answer: slope = -3/7
Step-by-step explanation:
m(slope) = (y2-y1)/(x2-x1)
m = (-2+-1)/(5--2)
m = (-2-1)/5+2)
m = -3/7
The first three terms of a sequence are given. Round to the nearest thousandth (if necessary).
9,16,23,...
Find the 46th term.
Answers
The 46th term of the sequence is 324.
We have,
To find the 46th term of the sequence, we need to determine the pattern or rule that generates the terms.
Since the difference between consecutive terms is a constant value of 7, we know that this is an arithmetic sequence with a common difference
of 7.
To find the 46th term, we can use the formula for the nth term of an arithmetic sequence:
a(n) = a(1) + (n - 1) d
where a(1) is the first term, d is the common difference, and n is the term number we want to find.
Using the given information, we have:
a(1) = 9
d = 7
n = 46
Plugging these values into the formula, we get:
a (46) = 9 + (46 - 1)7
a (46) = 9 + 45 (7)
a(46) = 9 + 315
a(46) = 324
Therefore,
The 46th term of the sequence is 324.
Learn more about arithmetic sequence here:
https://brainly.com/question/10396151
#SPJ1
Akeem is carrying water in a bucket, but is unsure how many gallons it holds. He knows that the bucket and water weigh 32.49 pounds together. The bucket alone weighs 2.61 pounds and the water weighs 8.3 pounds per gallon. How many gallons of water is Akeem carrying? Add or divide?
Answers
Answer:
Step-by-step explanation:
8.3g+2.61=32.49
8.3g=29.88
g=3.6
16. What product is represented with the following Algebra Tiles?
(2x²+6) (4x+6)
(4x + 4) (6x + 6)
(2x + 2)(2x + 3)
4x+10

Answers
The product that is represented with the algebra tiles is (2x + 2)(2x + 3)
Finding the product that is represented with the algebra tiles?From the question, we have the following parameters that can be used in our computation:
The algebra tiles
Representing the red tile with digit 1
So, we have
Vertical = 2x + 1 + 1 = 2x + 2
Horizontal = 2x + 1 + 1 + 1 = 2x + 3
The product that is represented with the algebra tiles is then calculated as
Product = Vertical * Horizontal
So, we have
Product = (2x + 2)(2x + 3)
Hence, the product is (2x + 2)(2x + 3)
Read more about algebra tiles at
https://brainly.com/question/28147007
#SPJ1
what is the property of 3x(5x7)=(3x5)7
Answers
The property you are referring to is called the associative property of multiplication. According to this property, when multiplying three numbers, the grouping of the numbers does not affect the result. In other words, you can change the grouping of the factors without changing the product.
In the equation you provided: 3x(5x7) = (3x5)7
The associative property allows us to group the factors in different ways without changing the result. So, whether we multiply 5 and 7 first, or multiply 3 and 5 first, the final product will be the same.
The circumference would ……. For example, a circle with a radius of 3 feet would have a circumference that is about 18 feet. When the radius doubles to 6 feet, the circumference is about ………. feet.
Answers
Answer:
37.7 feet
Step-by-step explanation:
The circumference of a circle can be calculated using the formula: Circumference = 2 * π * radius, where π (pi) is approximately 3.14159.
For example, if we have a circle with a radius of 3 feet, its circumference would be approximately 18.85 feet (rounded to five decimal places).
When we double the radius to 6 feet, the circumference also doubles. In this case, the circumference would be approximately 37.70 feet (rounded to five decimal places).
In summary, when the radius of a circle doubles, the circumference also doubles, maintaining a direct proportional relationship between the two measurements.
A marching band needs to raise $13,500 for a trip to the Rose Bowl. The director told the band members that one-third of the amount that has been raised so far is equal to half of the amount that is still needed. How much more money needs to be raised for the trip?
Answers
Answer: $5400
Step-by-step explanation:
x = amount raised so far
13500 - x = amt. still needed
x/3 = (13500 - x)/2
2x = 3(13500 - x)
2x = 40500 - 3x
5x = 40500
x = 40500/5 = 8100 (amt. raised so far)
13500 - 8100 = 5400 (amt. still needed)
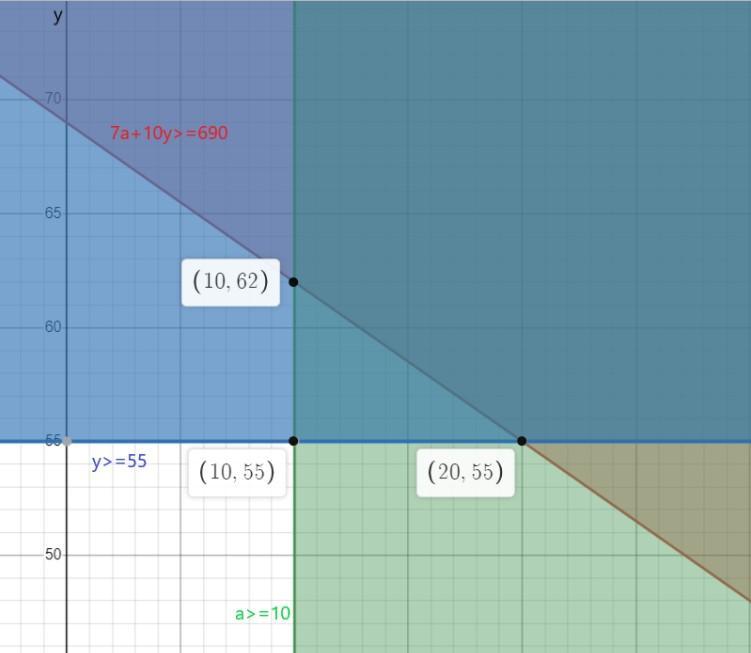
The drama club is selling tickets to their play to raise money for the show's expenses.
Each student ticket sells for $7 and each adult ticket sells for $10. The auditorium can
hold no more than 85 people. The drama club must make no less than $690 from
ticket sales to cover the show's costs. Also, they must sell a minimum of 10 student
tickets and at least 55 adult tickets. If a represents the number of student tickets sold
and y represents the number of adult tickets sold, write and solve a system of
inequalities graphically and determine one possible solution.

Answers
On solving the inequalities a ≥ 10, y ≥ 55, 7a + 10y ≥ 690, the solution is obtained as (20,55).
What is an inequality?
In Algebra, an inequality is a mathematical statement that uses the inequality symbol to illustrate the relationship between two expressions. An inequality symbol has non-equal expressions on both sides. It indicates that the phrase on the left should be bigger or smaller than the expression on the right, or vice versa.
Use the variables a and y to represent the number of student and adult tickets sold, respectively.
Then write the following system of inequalities -
a ≥ 10 (they must sell a minimum of 10 student tickets)
y ≥ 55 (they must sell at least 55 adult tickets)
7a + 10y ≥ 690 (they must make no less than $690 from ticket sales)
The first two inequalities are constraints on the number of tickets sold, and the third inequality represents the revenue constraint.
To find a possible solution, graph these inequalities on a coordinate plane and look for the feasible region that satisfies all three inequalities.
Alternatively, solve the system of inequalities using algebra.
First, simplify the third inequality by subtracting 7a from both sides -
10y ≥ 690 - 7a
Then, divide both sides by 10 -
y ≥ (690 - 7a)/10
This inequality represents the revenue constraint in terms of the number of student tickets sold.
Now combine the revenue constraint with the other two constraints -
a ≥ 10
y ≥ 55
y ≥ (690 - 7a)/10
Use substitution to solve for a in terms of y -
y ≥ (690 - 7a)/10
10y ≥ 690 - 7a
7a ≥ 690 - 10y
a ≥ (690 - 10y)/7
To find a possible solution, substitute a = (690 - 10y)/7 into the other two constraints -
(690 - 10y)/7 ≥ 10
y ≥ 55
These inequalities can be simplified -
690 - 10y ≥ 70
y ≥ 55
The first inequality can be solved for y -
-10y ≥ -620
y ≤ 62
Since it is known y ≥ 55, the feasible values for y are between 55 and 62, inclusive -
55 ≤ y ≤ 62
Now use the expression for a in terms of y to find the corresponding values of a -
a = (690 - 10y)/7
For each value of y between 55 and 62, inclusive, we can calculate a and check whether it satisfies the constraints -
a ≥ 10
y ≥ 55
7a + 10y ≥ 690
For example, when y = 55 -
a = (690 - 10(55))/7 = 20
7a + 10y = 7(20) + 10(55) = 690
Therefore, these values satisfy all three constraints, so one possible solution is a = 20 and y = 55.
To learn more about inequality from the given link
https://brainly.com/question/11234618
#SPJ1
(6d+1)^{ 2}+12=13\)
Answers
Answer:
This is not an Answer but i have to say: I hope this helps :b
Step-by-step explanation:
![(6d+1)^{ 2}+12=13[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/9wwLFrSvL6VVcHE3VGmMWA666zZk4uCk.png)
One angle of a right triangle measures 45°. What is the measure of the other acute angle?
Answers
Answer:
Below
Step-by-step explanation:
EVERY triangle's angles add up to 180 degrees
a RIGHT triangle has a 90 degree angle
this right triangle also has a 45 degree angle
let x° = third angle
90° + 45° + x° = 180°
x = 180 - 90 - 45 = 45 degrees
What is the value of x + y when x is the additive identity and y = 5?
O 5
O There is not enough information to determine the value.
O - 5
O 0
Answers
Answer:
-5.
Step-by-step explanation:
5 + -5 = 0, so i's -5.
h
– -1 = -3
6
what is the answer
Answers
Answer:
-36
Step-by-step explanation:
Explanation:
What is 2,001÷83 pls help i need to check my answer
Answers
Answer:
24.11
Step-by-step explanation:
2001 ÷ 83
83×2= 166
200-166=34 bring down the 1
341 ÷ 83
83×4= 332
341-332=9 add a decimal and bring down a 0
90÷83
90-83=7 bring down another 0
70÷83=0 brind down another 0 since 70 cannot be divided by 83 and have a whole number
700÷83
83×8=664
700-664=36
right now you have 24.108
round to the nearest tenth
24.11
What is the answer pls for this is hard

Answers
Answer:
125.6 units = x
Step-by-step explanation:
72
---- = tan 37 degrees, so x = 72/(tan 37 degrees)
x
This comes out to x = 72/0.573 = 125.6 units = x
A - on the po boyds at a emase the foot, 1, of building. He. Observes an obje- et on the top, P of the building at an angle of ele- building of 66 Aviation of 66 Hemows directly backwards to new point C and observes the same object at an angle of elevation of 53° · 1P) |MT|= 50m point m Iame horizontal level I, a a
Answers
Answer:
53\(x_{123}\) == 134 cf
Step-by-step explanation:
A - on the po boyds at a emase the foot, 1, of building. He. Observes an obje- et on the top, P of the building at an angle of ele- building of 66 Aviation of 66 Hemows directly backwards to new point C and observes the same object at an angle of elevation of 53° · 1P) |MT|= 50m point m Iame horizontal level I, a a
The height of the building is approximately 78.63 meters.
The following is a step-by-step explanation of how to solve the problem. We'll need to use some trigonometric concepts and formulas to find the solution.
Draw a diagram of the situation described in the problem to get a better understanding of the problem. The diagram would have a right-angled triangle with angle of elevation of 66° at the bottom left vertex and another angle of elevation of 53° at the bottom right vertex. The object on top of the building is at the vertex of the triangle. Point M and I on the diagram are points on the horizontal line of sight and on the ground respectively. We can label the diagram with the following values:Angle of elevation from point A = 66°Angle of elevation from point P = 53° Length of line segment AM = h Length of line segment MP = x Length of line segment IP = y Length of line segment MT = 50m. We'll use these values to calculate the length of h, which is the height of the building.Use the tangent ratio to find x:tan 66° = h / x => x = h / tan 66°. Use the tangent ratio to find y:tan 53° = h / y => y = h / tan 53°.We know that x + y = 50, so substituting the expressions for x and y from step 3 gives:h / tan 66° + h / tan 53° = 50h = 50 tan 66° tan 53° / (tan 53° + tan 66°) ≈ 78.63 m.Therefore, the height of the building is approximately 78.63 meters.
For more such questions on height, click on:
https://brainly.com/question/28122539
#SPJ8
Dan earns $42.75 per month working as a tutor. He worked as a tutor for 4 months. He also earned $52.45 walking dogs in the neighborhood. He spent $18.50 of his total earning to buy a movie ticket and candy. Dan put of the remaining money in his savings account.
Answers
Answer:
204.95
Step-by-step explanation:
42.75x4=171
171+52.45=223.45
223.45-18.5=204.95
Step-by-step explanation:
Dan made an error in step 2 he added the 18.50 instead of subtracting. it should be 171+52.45= 223.45 223.45-18.50 = 204.95
Solve for x leave your answer in simplest radical form

Answers
Answer:
X=11 trust me on my mom
express 2 cos 35 sin 67 as a sum
Answers
2 cos 35 sin 67 can be expressed as the sum of sin(102) and -sin(32).
To express 2 cos 35 sin 67 as a sum, we can use the trigonometric identity for the product of two sine or cosine functions.
Specifically, the identity states that 2 cos A sin B can be written as
sin(A + B) + sin(A - B).
Applying this identity, we have:
2 cos 35 sin 67 = sin(35 + 67) + sin(35 - 67)
Simplifying the expressions inside the sine functions:
sin(102) + sin(-32)
Since the sine function is an odd function,
sin(-x) = -sin(x),
so we can rewrite the equation as:
sin(102) - sin(32)
Therefore, 2 cos 35 sin 67 can be expressed as the sum of sin(102) and -sin(32).
For such more questions on trigonometric identity
https://brainly.com/question/7331447
#SPJ8
Solve the system of equations:
X+y+z=5
-3x-4y+4z=15
2x-y-4z=-8
Answers
Answer:
(x, y, z) = (3, -2, 4)
Step-by-step explanation:
The attachment shows a solution using a graphing calculator where the first equation is solved for z, and that expression is substituted into each of the other two equations. The solution to that system is (x, y) = (3, -2). Using these values in the expression for z, we find ...
z = 5 -(3 +(-2)) = 4
The solution is (x, y, z) = (3, -2, 4).
__
Your graphing calculator and/or online tools can give you the reduced row echelon form of the augmented matrix representing the system:
\(\left[\begin{array}{ccc|c}1&1&1&5\\-3&-4&4&15\\2&-1&-4&-8\end{array}\right]\)
__
If you're solving by hand, you can do the substitution described above to eliminate z from one equation. You can eliminate z from another equation by adding the last two:
-3x -4y +4(5 -x -y) = 15 ⇒ -7x -8y = -5
(-3x -4y +4z) +(2x -y -4z) = (15) +(-8) ⇒ -x -5y = 7
This pair of equations can be solved for x and y in any of the usual ways. Using the second equation to substitute for x, for example, gives you ...
-7(-5y -7) -8y = -5 ⇒ 27y = -54 ⇒ y = -2
x = -5(-2) -7 = 3
z = 5 -(3) -(-2) = 4
_____
Additional comment
If all that is needed is a solution, we prefer a graphical or matrix approach. These take about the same amount of time. Both require a little additional effort to determine exact values when the solutions are not integers.

The endpoints of PC are P(4, 1) and Q(4,8). Find the midpoint of PQ
A. (4, 4.5)
B. (0, -3.5)
C. (4.5, 4)
D. (6, 3.5)
Answers
Answer:
A. (4,4.5)
Step-by-step explanation:
Midpoint={x1+x2/2,y1+y2/2}
M={4+4/2,1+8/2}
M={8/2,9/2}
M={4,4.5}