The triangles are similar, which angle is congruent to
Answers
Jacob, this is the solution:
Step 1: Let's recall that the two vertex angles of these two triangles are equal, according to the Vertical angles theorem.
Step 2: Triangles POQ and MON are congruent, in consequence:
Angles O for both triangles are equa.l
Angles M, N, P and Q are also equal.
Thus M = P = Q.
Related Questions
9. A has some amount of money with him. He gave one half of one third from that amount One half of the amount received by B is 20. What is the amount that A originally had?
Answers
Using the expression 5x/12 = 20, the amount that A originally had was $48.
We have,
Let x be the amount of money that A originally had.
Then, A gave away 1/2 x 1/3 = 1/6 of the amount, which is equal to x/6.
The amount received by B is 1/2 of the remaining amount,
which is (x - x/6)/2 = 5x/12.
We know that 5x/12 = 20,
Solving for x.
5x/12 = 20
5x = 240
x = 48
Therefore,
The amount that A originally had was $48.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
COULD YALL HELP ME ?!???!

Answers
Answer:
28 degrees
Step-by-step explanation:
We know that (4x + 7) + (2x + 5) add up to a straight angle = 180 degrees, so we have the equation 4x + 7 + 2x + 5 = 180.
By combining like terms, we get 6x + 12 = 180.
Subtract 12 from both sides of the equation to get 6x = 168. Divide both sides by 6 and you get x = 28.
i Must
Illustr
Mathe
E
DATE
PE
Consider a function q defined by q(x) = x2. Explain why negative valu
are not include in the range of q. (From Unit 4, Lesson 10.)
Answers
Answer:
Step-by-step explanation:
The simple short answer is because all real numbers are to be squared.
If any negative value is put into x^2, the value will become positive. That's because an even number of negatives are positive.
For example y = x * x
Let x = - 3
y = (-3)(-3)
y = 9 because there are an even number of negatives.
Notice that if break x^2 into x * x, you should see more clearly that each x is equal to - 3
A fox, who has a start of 60 leaps, is chased by a dog, the. fox can make 3 leaps to the dogs 2. However, the dog travels in only 3 leaps as far as the fox goes in 7. How many leaps must each make before the fox is caught by the dog.
Answers
Both the fox and the dog need to make 28 leaps before the fox is caught.
Given that,
The fox has a start of 60 leaps.
The fox can make 3 leaps to the dogs 2.
This means that for every 3 leaps taken by the fox, the dog will take 2.
The dog travels in only 3 leaps as far as the fox goes in 7.
This means that for every 3 leaps the dog takes, the fox takes 7 leaps.
Now, we have to find out how many leaps the fox and the dog need to make before the fox is caught.
Assume that the fox and the dog both sprint for "x" number of jumps before the fox is apprehended.
For the fox,
The total distance travelled would be ⇒ 60 + 3x
(since the fox can make 3 leaps for every 2 leaps of the dog, and the fox starts with a 60-leap advantage).
For the dog,
The total distance travelled would be ⇒ 2x
(since the dog can make 2 leaps for every 3 leaps of the fox).
Now we know that the dog travels in only 3 leaps as far as the fox goes in 7,
Therefore,
3 leaps of the dog = 7 leaps of the fox
This can be expressed as:
2x = (60 + 3x)( 7/3 )
Simplifying this equation, we get:
2x = 140 + 7x
5x = 140
x = 28
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ1
Determine the domain and range of the graph

Answers
Answer:
5 ≤ x ≤ 10 5 ≤ y ≥ -1
Step-by-step explanation:
7. Jackson missed 2 out of every 9 questions on a 45-question test. How many questions did
Jackson get correct?
(1) 90
(2) 35
(3) 29
(4) 10
Answers
HELLLLPPPPP!!!!!!!!!!!! AHHHHHHHHHHH!!!!!!!
kenji is raising baby kittens. their weights after three weeks are 12 ounces, 14 ounces, 15 ounces, 15, ounces and 14 ounces, what is the mean weight of the kittens????
Answers
Answer: 14 ounces
Step-by-step explanation:
To find the mean, we add up all the values and divide by the number of values.
\(\displaystyle \frac{12+14+15+15+14}{5} =\frac{70}{5} =14\;ounces\)
What is 2/9 simplified?
Answers
_
0.2
which congruence theorem can be used to prove wxz yzx
Answers
The congruence theorem that proves that ΔWXZ ≅ ΔYZX is: a.AAS
What does a math congruent mean?
Congruent refers to having precisely the same form and size. Even after the forms have been flipped, turned, or rotated, the shape and size ought to remain constant.
The image given shows that
∠W ≅ ∠Y
∠X ≅ ∠Z
XZ ≅ XZ
Therefore, the congruence theorem that proves that ΔWXZ ≅ ΔYZX is: a.AAS
Learn more about Congruent
brainly.com/question/12413243
#SPJ4

Trigonometry: Measure tal Excel In Opt. Mathematics - Book 9 ) If the number of degrees of a certain angle added to the number of gra same angle is 152, find the angle in degrees.
Answers
The angle in degrees is 873.1843.
Let the measure of the angle be θ in degrees. Therefore, the measure of the same angle in gradians is (θ × π/180).
According to the given information, the number of degrees of a certain angle added to the number of gradians of the same angle is 152.(θ) + (θ × π/180) = 152.
Simplifying the above equation, we get:(θ) + (θ/180 × π) = 152.
Multiplying both sides of the equation by 180/π, we get:
θ + θ = (152 × 180)/π2θ = (152 × 180)/πθ = (152 × 180)/(3.14)θ = 873.1843
Thus, the angle in degrees is 873.1843.
For more such questions on angle, click on:
https://brainly.com/question/25770607
#SPJ8
Find the accumulated value of an investment of $14,000 at 10% compounded semiannually for 11 year
Answers
Given:
Principal = $14000
Rate of interest = 10% compounded semiannually.
Time = 11 years.
To find:
The accumulated value of the given investment.
Solution:
Formula for amount or accumulated value after compound interest is:
\(A=P\left(1+\dfrac{r}{n}\right)^{nt}\)
Where, P is the principal values, r is the rate of interest in decimal, n is the number of times interest compounded in an year and t is the number of years.
Compounded semiannually means interest compounded 2 times in an years.
Putting \(P=14000,r=0.10,n=2,t=11\) in the above formula, we get
\(A=14000\left(1+\dfrac{0.10}{2}\right)^{2(11)}\)
\(A=14000\left(1+0.05\right)^{22}\)
\(A=14000\left(1.05\right)^{22}\)
\(A\approx 40953.65\)
Therefore, the accumulated value of the given investment is $40953.65.
Answer:
A = $41,867.06
A = P + I where
P (principal) = $14,000.00
I (interest) = $27,867.06
Step-by-step explanation:
Given: Investment = $14,000 Annual Rate: 10% compounded semiannually = 11 year
To find: The accumulated value of an investment
Formula: \(A = P(1 + \frac{r}{n}) ^n^t\)
Solution: First, convert R as a percent to r as a decimal
r = R/100
r = 10/100
r = 0.1 rate per year,
Then solve the equation for A
A = P(1 + r/n)nt
A = 14,000.00(1 + 0.1/12)(12)(11)
A = 14,000.00(1 + 0.008333333)(132)
A = $41,867.06
Henceforth:
The total amount accrued, principal plus interest, with compound interest on a principal of $14,000.00 at a rate of 10% per year compounded 12 times per year over 11 years is $41,867.06.
LESSON 17 SESSION 3
4 Ms. Duda's class is hanging 500 red lanterns around the
school for Lunar New Year. Before lunch, the class hangs
100 of the lanterns.
PART A Draw a model to show what percent of 500 lanterns
the class hangs before lunch.
Answers
The model should visually represent that Ms. Duda's class hung 100 lanterns before lunch, which is 20% of the total 500 lanterns.
To draw a model showing what percent of 500 lanterns Ms. Duda's class hangs before lunch, we can use a rectangular bar model.
Draw a rectangular bar to represent the total number of lanterns, which is 500. Label it as "Total Lanterns."
Divide the rectangular bar into two parts. One part should represent the number of lanterns hung before lunch, which is 100. Label this section as "Lanterns Before Lunch."
Calculate the percentage of lanterns hung before lunch by dividing the number of lanterns hung before lunch by the total number of lanterns and multiplying by 100. In this case, (100/500) * 100 = 20%.
Draw an arrow pointing to the "Lanterns Before Lunch" section, and write "20%" next to it to represent the percentage.
The model should visually represent that Ms. Duda's class hung 100 lanterns before lunch, which is 20% of the total 500 lanterns.
To learn more about the percentage;
https://brainly.com/question/24159063
#SPJ1
Explain in detail using words the step by step process that Maggie took to solve the problem 6.89 x 10^-4 / 7.5 x 10^-6 = .92 x 10^1
Answers
The steps in solving the given expression shows that the result is:
0.92 * 10²
How to use Laws of Exponents?The expression is given as:
6.89 * 10⁻⁴/(7.5 * 10⁻⁶) = 0.92 * 10¹
The steps that Maggie followed are:
Step 1: Rewrite the given expression:
6.89 * 10⁻⁴/(7.5 * 10⁻⁶) = 0.92 * 10¹
Step 2: Divide the coefficients:
The coefficient of the numerator (6.89) is divided by the coefficient of the denominator (7.5) to get:
6.89 / 7.5 = 0.9186667.
Step 3: Divide the powers of 10:
This is done by subtracting the exponent of the denominator 10⁻⁶ from the exponent of the numerator 10⁻⁴ to get: 10²
Step 4: Combine the results:
This gives:
0.9186667 * 10²
Step 5: Simplify the coefficient:
She rounded the coefficient (0.9186667) to two decimal places, resulting in 0.92.
Read more about Laws of Exponents at: https://brainly.com/question/11761858
#SPJ1
84.4% of what number is 19.412?
Answers
Answer: 22.4402
Step-by-step explanation:
Answer:
84.4% of 23 is 19.412.
Step-by-step explanation:
Let the unknown number be x.
Now, 84.4% of x = 19.412.
∴ (84.4 ÷ 100) × x = 19.412.
By simplifying the equation,
x = (19.412 × 100) ÷ 84.4
x = 1941.2 ÷ 84.4
∴ x = 23
Thus, 84.4% of 23 is 19.412.
To learn more about Percentages,
refer to the following question!
https://brainly.com/question/3079428
Can some help me please I did one but I am not sure if it is correct.
thank you
Answers
Answer:
yes its correct
Step-by-step explanation:
but for the check where did you get the 12? you might want to redo that part but otherwise its right
Someone help
A)17/15
B)15/17
C)17
D)8/17
E)17/8

Answers
Answer:
B) 15/17
Step-by-step explanation:
You want the sine of acute angle A in the right triangle shown.
SineThe sine of the angle is the ratio ...
Sin = Opposite/Hypotenuse
We can go to the trouble to figure the hypotenuse, or we can choose the only suitable answer from the list provided. (It is the one marked already.)
The leg lengths of the triangle shown are 8 and 15, with leg 15 being opposite angle A. This is the first clue that the ratio will have 15 in the numerator. Only answer choice B matches.
CheckThe value of the sine function is never greater than 1, eliminating answer choices A, C, and E, leaving choices B and D.
Since the side opposite angle A is the longest of the two legs, we know that angle A is more than 45°, and its sine is more than √2/2. That means choice D can be eliminated, since it is less than 1/2.
The sine of angle A is 15/17.
<95141404393>
can some one help me do this question
just give me e and f
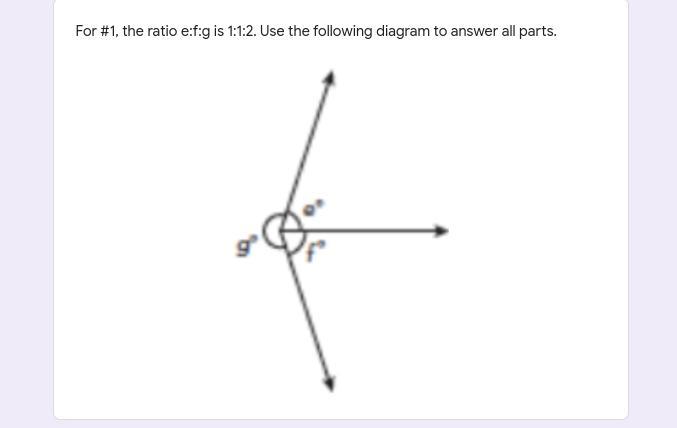
Answers
Answer:
I believe the answer should be 90:90:180. I may be wrong.
An arrow is shot from 3 ft above the top of a hill with a vertical upward velocity of 108 ft/s. If it strikes the plain below after 9.5 s, how high is the hill?
If the arrow is launched at t0, then write an equation describing velocity as a function of time?
Answers
The height of the hill is approximately 25.73 ft. Where v0 is the initial velocity (108 ft/s), g is the acceleration due to gravity \((-32.2 ft/s^2)\),
To find the height of the hill, we can use the formula for the vertical position of an object under constant acceleration:
h = h0 + v0t + 1/2at^2
where h is the final height, h0 is the initial height, v0 is the initial velocity, t is the time, and a is the acceleration due to gravity (-32.2 ft/s^2).
In this case, we are given that the initial height h0 is 3 ft, the initial velocity v0 is 108 ft/s, and the time t is 9.5 s. We want to find the height of the hill, which we can denote as h_hill. The final height is the height of the plain, which we can denote as h_plain and assume is zero.
At the highest point of its trajectory, the arrow will have zero vertical velocity, since it will have stopped rising and just started to fall. So we can set the velocity to zero and solve for the time it takes for that to occur. Using the formula for velocity under constant acceleration:
v = v0 + at
we can solve for t when v = 0, h0 = 3 ft, v0 = 108 ft/s, and a = -32.2 ft/s^2:
0 = 108 - 32.2t
t = 108/32.2 ≈ 3.35 s
Thus, it takes the arrow approximately 3.35 s to reach the top of its trajectory.
Using the formula for the height of an object at a given time, we can find the height of the hill by subtracting the height of the arrow at the top of its trajectory from the initial height:
h_hill = h0 + v0t + 1/2at^2 - h_top
where h_top is the height of the arrow at the top of its trajectory. We can find h_top using the formula for the height of an object at the maximum height of its trajectory:
h_top = h0 + v0^2/2a
Plugging in the given values, we get:
h_top = 3 + (108^2)/(2*(-32.2)) ≈ 196.78 ft
Plugging this into the first equation, we get:
h_hill = 3 + 108(3.35) + 1/2(-32.2)(3.35)^2 - 196.78
h_hill ≈ 25.73 ft
If the arrow is launched at t0, the equation describing velocity as a function of time would be:
v(t) = v0 - gt
For such more questions on velocity
https://brainly.com/question/25749514
#SPJ8
Sam has a deck that is shaped like a triangle with a base of 18 feet and a height of 7 feet. He plans to build a 2:5 scaled version of the deck next to his horse's water trough.
Part A: What are the dimensions of the new deck, in feet? Show every step of your work. (4 points)
Part B: What is the area of the original deck and the new deck, in square feet? Show every step of your work. (4 points)
Part C: Compare the ratio of the areas to the scale factor. Show every step of your work. (4 points)
Answers
The 2 : 5 scaled version of the deck Sam plans to build and the dimensions of the original deck indicates;
Part A; Base length of the new deck = 7.2 feet
Height of the new deck = 2.8 feet
Part B; The area of the original deck is 63 square feet
The area of the new deck is 10.08 square feet
Part C; The ratio of the areas is the square of the scale factor
What is a scale factor?A scale factor is a number or factor that is used to enlarge or reduce the dimensions a shape or size of a figure.
The base length of the triangular deck = 18 feet
The height of the triangular deck = 7 feet
The scale factor for the scaled version Sam intends to build = 2 : 5
Part A; The dimensions of the new deck are;
Base length of the new deck using the the 2 : 5 ratio is; (2/5) × 18 = 7.2 feet
The height of the new deck = (2/5) × 7 = 2.8 feet
Part B; The area of the original deck = (1/2) × 18 × 7 = 63 square feet
Area of the new dec = (1/2) × 7.2 × 2.8 = 10.08 square feet
Part C; The ratio of the areas is; 10.08/63
Ratio of the area = 10.08/63 = 4/25 = 4 : 25
The scale factor is; 2 : 5
Therefore, the ratio of the area is the square of the scale factorLearn more on scale factors here: https://brainly.com/question/28822248
#SPJ1
Factor 5x2y + 22xy – 15y.
Answers
Answer:
5y(x^2 - 3)
Step-by-step explanation:
Hope this helps :)
Based on mathemAtical models, the chance of rain today is 60%. Is that theoretical or experimental.
Answers
Which of the following statements is true for the following data set?
7, 5, 6, 4, 7, 8, 12
a. Only the mean and median are equal.
b. Only the mean and mode are equal.
c. Only the median and mode are equal.
d. The mean, median, and mode are all equal.
Answers
Answer:
D.
Step-by-step explanation:
Mean : 7 + 5 + 6 + 4 + 7 + 8 + 12 = 12 + 10 + 7 + 20 = 30 + 19 = 49. 49/7= 7
Mode : 7.
Median 4 , 4, 6, 7, 7, 8, 12. 7 is the middle number
Which of the following systems of inequalities has point D as a solution?

Answers
Answer:
f(x) \(\leq\) 3x + 4
g(x) ≥ -1/2x - 5
Step-by-step explanation:
Point D is below f(x) and above g(x)
Helping in the name of Jesus.
John's paycheck this week was $9.23 less than his paycheck last week. His paycheck this week was $154.01. How much was John's paycheck last week?
Answers
Answer:
$163.24
Step-by-step explanation:
you have to add the two values together since his paycheck last week was MORE than his paycheck this week.
154.01+9.23= 163.24
Please solve this math question.

Answers
Answer:
none of these
Step-by-step explanation:
the side lengths are are 2√5/5, 2, and 4.
sin(x) = opp/hyp
sin(x) = 2/2√5
please help):
Estimate the product of 408 - 52 by first rounding each number to the nearest ten.
A: 20,000
B: 460
C: 450
D: 20, 500
Answers
Answer: 20500
Step-by-step explanation:
Rounding 408 to the nearest ten will give 410. Since it is above 4, we'll add 1 to the 0 in the tens value and this will be 410.
Rounding 52 to nearest ten is 50.
Therefore, we'll multiply 410 by 50. This will be:
= 410 × 50
= 20500
Therefore, the correct option is D.
6. Meryll made a pancake with a circumference of 125.6 cm. What is its area? (A) 884 cm² (B) 1 256 cm² (C) 1 468 cm²
Answers
Answer:
(B) 1256 cm²---------------
Let the radius be r.
Use circumference formula and find the value of r:
C = 2πr125.6 = 2*3.14rr = 125.6/6.28r = 20Find the area using the circle area formula:
A = πr²A = 3.14*20²A = 1256The matching choice is (B).
Answer:
Step-by-step explanation:

How does the graph of g(x) = (x + 2)3 − 6 compare to the parent function of f(x) = x3? g(x) is shifted 2 units to the right and 6 units down. g(x) is shifted 6 units to the right and 2 units up. g(x) is shifted 2 units to the left and 6 units down. g(x) is shifted 6 units to the left and 2 units down.
Answers
Answer:
The function g(x) = (x + 2)³ − 6 is obtained by applying three transformations to the parent function f(x) = x³.
First, g(x) is shifted 2 units to the left by subtracting 2 from x inside the parentheses:
g(x) = (x + 2 - 2)³ − 6 = (x)³ − 6
This shows that option C, "g(x) is shifted 2 units to the left and 6 units down," is not correct.
Next, g(x) is shifted 6 units down by subtracting 6 from the entire function:
g(x) = (x + 2)³ − 6 - 6 = (x + 2)³ - 12
This shows that option A, "g(x) is shifted 2 units to the right and 6 units down," is correct.
Finally, g(x) is not shifted left or right by any additional units, but it is shifted 2 units up by adding 2 to the constant term:
g(x) = (x + 2)³ − 6 + 2 = (x + 2)³ - 4
This shows that option B, "g(x) is shifted 6 units to the right and 2 units up," is not correct.
Therefore, the correct answer is option A: g(x) is shifted 2 units to the right and 6 units down.
Calculate the distance between the points P=(1, -1) and N=(5, -8) in the coordinate plane.
Round your answer to the nearest hundredth.
PLEASE PLEASE HELP ME

Answers
\(~~~~~~~~~~~~\textit{distance between 2 points} \\\\ P(\stackrel{x_1}{1}~,~\stackrel{y_1}{-1})\qquad N(\stackrel{x_2}{5}~,~\stackrel{y_2}{-8})\qquad \qquad d = \sqrt{( x_2- x_1)^2 + ( y_2- y_1)^2} \\\\\\ PN=\sqrt{(~~5 - 1~~)^2 + (~~-8 - (-1)~~)^2} \implies PN=\sqrt{(5 -1)^2 + (-8 +1)^2} \\\\\\ PN=\sqrt{( 4 )^2 + ( -7 )^2} \implies PN=\sqrt{ 16 + 49 } \implies PN=\sqrt{ 65 }\implies PN\approx 8.06\)
solve this question please

Answers
Answer:
Step-by-step explanation:
a) 1.8 kg in grams is 1800 g
b) If 6 toys weigh 1800g; then 1 toy weighs 300 g(6:1)
c) If 1 toy weighs 300 g, 4 toys weigh 1200 g and you convert in kg which is 1.2 kg